基于图像技术的三轴土样径向变形测量

牟春梅， 杨 警， 范兰杨， 吴浩杰

(1.桂林理工大学土木与建筑工程学院， 桂林 541004； 2.广西岩土力学与工程重点实验室， 桂林 541004)

土工三轴试验测量土的变形和强度是一种较为完善的方法，但由于试验仪器和土样变形计算方法的限制，仍存在如下不足[1-3]：①常规测量方法得出的土样轴向变形和径向变形是整体的平均变形，实际上土样的变形是不均匀的；②土样的径向变形是由体积变化量和轴向变化量换算而来的，换算值不能反映出土样的实际径向变形。为克服上述问题，张鲁渝等[4]在三轴试验中运用霍尔效应传感器对三轴试样中部1/3区域的轴向和径向变形进行测量，有效地减小了端部约束的影响，得到了一些常规三轴仪观测不到的结果；陈超斌等[5]利用安装有LVDT(linear variable differential transformer)位移传感器的三轴仪对上海软土土样的局部变形进行测量，取得了良好的测量结果。霍尔效应传感器、LVDT位移传感器在对土样变形进行测量时，需要将传感器固定在三轴土样上，在接触部位难以避免的会对土样的变形产生制约。

随着图像测量技术的不断提升和研究的逐步深入，对土样进行非接触式测量的图像测量方法有望成为三轴土样变形测量的新趋势。Macari等[6]使用数字图像分析技术对三轴土样的变形进行非接触式测量，通过图像中土样的轮廓图像实现对土样轴向变形和径向变形的测量。Alshibli等[7]同时使用三台相机对三轴土样进行拍摄，利用图像的平面投影和X射线扫描，得到试样不同变形阶段的轴向变形，以及试样任意高度处的径向变形，重构三轴土样在不同轴向应力应变水平下的三维效果图。邵龙潭等[8]通过自主研制的新型多功能土工三轴试验仪对三轴土样的变形进行测量，经过追踪土样表面和试样边缘的角点确定土样的轴向变形和径向变形。图像测量的三轴试验是通过土样的数字图像来对土样的轴向变形、径向变形进行测量，无需与土样发生接触，避免了对三轴土样的扰动，并且数字图像测量方法可针对土样的任意部位进行变形测量，能够有效地克服常规三轴试验的缺陷。新型图像测量技术利用被摄物体不同视角下的数字图像，重构被摄物体的三维空间形态，从而实现对被摄物体的三维空间测量，克服传统图像测量方法局限于二维平面测量的限制。将新型图像测量方法运用于常规三轴试验中，通过引入径向折射修正系数来减小由于水、有机玻璃压力室折射引起的图像测量误差，变形场计算中对土样的横向和纵向应变进行测量[9]，可获得土样不同部位的局部变形数据以及土样不同部位处实际作用的轴向力的大小，并得到其应力应变曲线，实现土样的变形过程测量。

1 新型图像测量技术

1.1 世界坐标系的建立以及三维模型重构原理

试验前，分别将RAD(ringed automatically detected)编码点粘贴在包裹土样的橡皮膜表面和三轴仪的荷载架上，为了数据处理方便及分析一般选取荷载架一侧端处的编码点作为世界坐标系的原点建立世界坐标系(O-XYZ)(图1)，应用游标卡尺对荷载架上的编码点进行距离测量，定义世界坐标中模型的比例尺，实现模型与真实距离的对应关系。相机成像模型是描述二维像点与三维空间点之间映射关系的空间几何模型，针孔成像模型可认为是理想的相机成像模型。在针孔相机模型中存在一系列空间坐标系统：图像像素坐标系(A-mn)、图像像素物理坐标系(A-x′y′)、相机坐标系统(S-xyz)、世界坐标系(O-XYZ)，如图1所示。

图1 世界坐标系及针孔模型示意图Fig.1 Schematic diagram of world coordinate system and pinhole model

通过坐标系之间的几何关系建立三维空间物点与像点之间的投影关系。像点、物点的几何关系可以简单地概括为摄影空间中不同坐标系统的相互转换，具体是：物=E×像。E可以看作是摄像机成像的几何模型，E中的参数就是摄像机参数，包括相机的内部参数和外部参数。相机内部参数表示相机的光学和几何特征，主要包括图像传感器的大小(Fx，Fy)、图像传感器的像素单元总数(M×N)、像主点坐标(Px，Py)、焦距(f)。利用计算机图像处理算法识别预先在被摄物体表面设置的摄影标志点，获得摄影标志点的图像像素坐标，使用相机内部参数可将图像像素坐标系统中的平面坐标点转换为相机坐标系统中的三维坐标点[10]，转换关系为

(1)

(2)

式中：(mI,nI)表示空间点I在图像像素坐标系中的坐标；(x′I,y′I)表示空间点I在图像像素物理坐标系中的坐标；(xI,yI,zI)表示空间点I在相机坐标系中的坐标。

相机外部参数是三维世界坐标系与相机坐标系的变化参数，包括旋转矩阵R(ωφκ)和平移矩阵(XS,YS,ZS)，利用相机外部参数将相机坐标系统中的三维坐标点换算为世界坐标系中的三维坐标点，转换关系[11]为

(3)

R(ωφκ)=

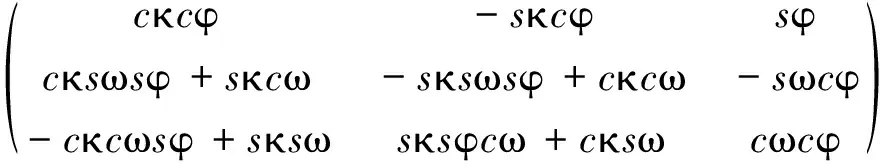
(4)

式中：(XI,YI,ZI)表示空间点I在世界坐标系中的坐标；R(ωφκ)为旋转矩阵,ω、φ、κ为相机坐标系各坐标轴的旋转角；X轴的旋转角度为ω，Y轴的旋转角度为φ，Z轴的旋转角度为κ；c为余弦cos,s为正弦sin。

在单相机成像模型中，应用物点、像点、光心之间的共线关系，可推断得到的三维空间点位于光心与像点构成的延长线上，但无法确定三维空间点在三维空间中的深度信息。由此，在单相机成像模型基础上形成多相机成像模型，利用被摄物体不同视角下的数字图像，通过图像间的几何关系构建共线方程[12]，求解旋转矩阵和平移向量，一旦旋转矩阵与平移向量确定，即可通过不同图像的视觉交汇，运用最小二乘法确定最终的三维点坐标[13]，如图2所示。

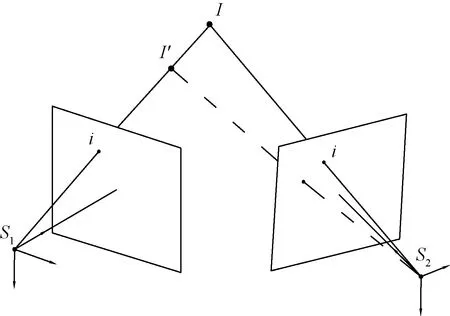
S1为第一个相机点；S2为第二个相机点；i为光线透过图像平面的点； I′为I修正前的点位置；I为运用视觉交汇，最小二乘法修正后的点位置图2 双相机成像模型Fig.2 Dual camera imaging model

1.2 图像测量技术的测量精度

运用图像测量技术对被摄物体进行三维重构，检测其对三维空间物体的重建精度，选用游标卡尺和图像测量方法对同一刚性圆柱体进行轴向和径向的测量，测量结果详见表1。由表1可知，图像测量与游标卡尺的测量结果基本一致，轴向测量以及径向测量的相对测量误差为0～0.02 mm，可知图像测量技术能够对三维物体实现高精度的三维立体测量。

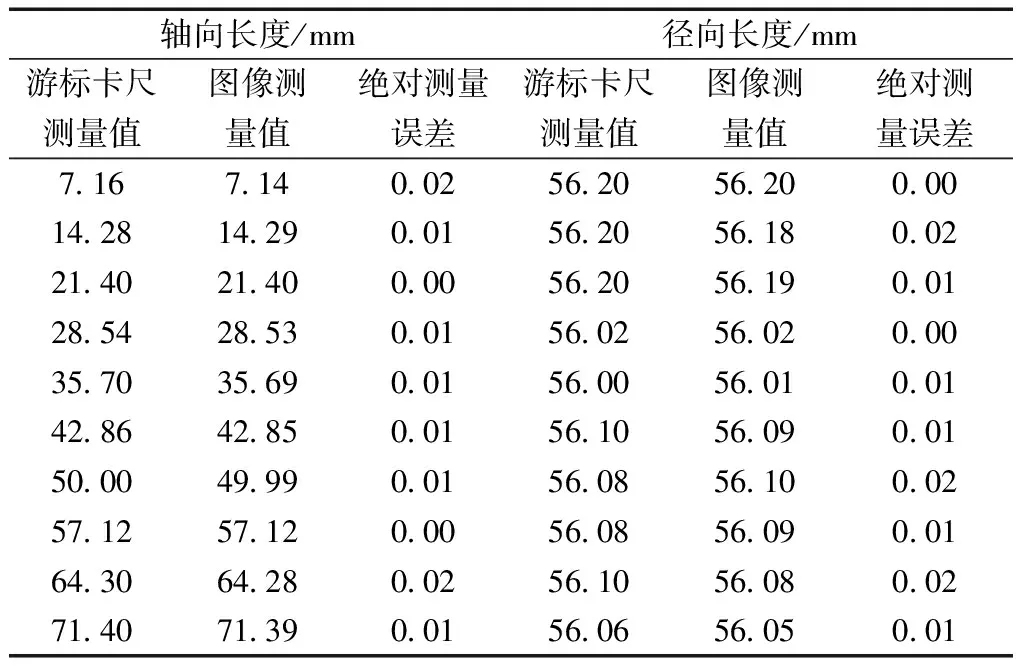
表1 土样的轴向及径向测量结果统计表Table 1 Statistical table of axial and radial measurement results of soil samples

2 图像测量折射误差修正

三轴土样在压力室中的成像光线被相机捕获成像前，传播路径为水→压力室罩→空气→相机，如图3所示，压力室内土样上部没被水淹没部分与下部对比发现，下部图像被明显放大，导致测得的土样径向变形量相对于实际变形量是变大的。压力室罩和水的折射影响是图像测量误差的主要因素，该影响在计算土样变形量时须将所得测量值除以相应的修正系数的方法给予消除。三轴压力室为圆柱形，在轴向平面上，压力室如同一平面板玻璃，折射对轴向测量的影响较小；在径向上，有机玻璃压力室为一弧形曲面，圆柱体的径向图像被明显放大。将已知尺寸的圆柱体置于三轴仪底座之上，由于图像测量技术在空气中的测量精度与游标卡尺的测量精度相近，利用图像测量方法分别对空气中、压力室中的圆柱体进行轴向和径向上的测量，结果见表2及表3。

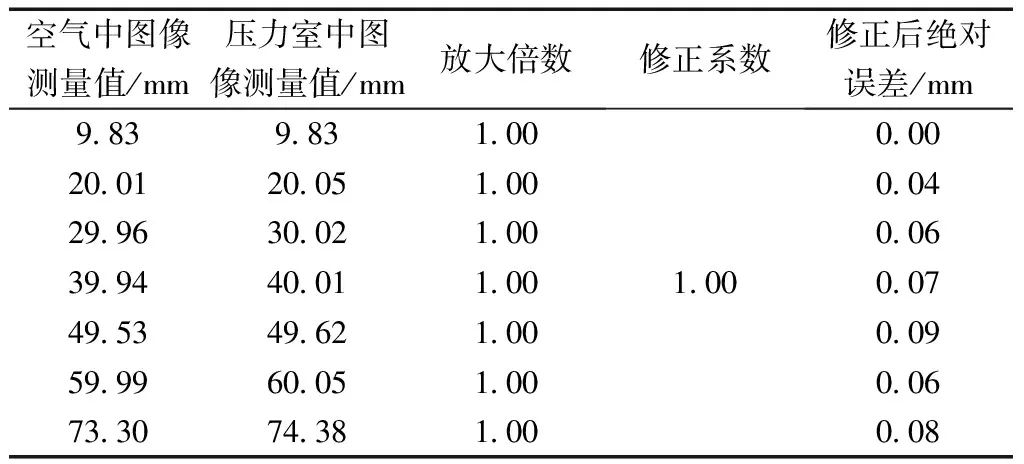
表2 不同轴向高度测量值Table 2 Different axial height measurements

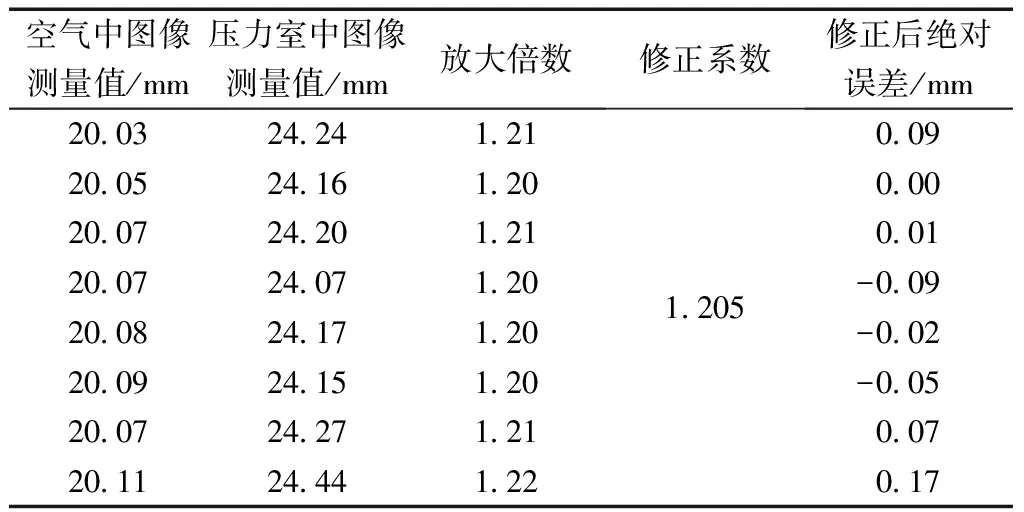
表3 径向测量值Table 3 Radial measurement

图3 土样被放大对比图Fig.3 Soil sample is enlarged and compared

从试验结果来看：①折射效应对土样的轴向长度测量的影响较小，测量结果与土样的实际长度大致相同，压力室中的图像测量值与土样的实际轴向高度基本一致，绝对测量误差为±0.09 mm，在三轴试验中，该测量误差可忽略不计，在计算土样的轴向变形时，无需考虑折射对轴向测量值的影响；②折射效应对土样的径向测量的影响很大，压力室中土样的图像测量值比土样的实际径向值大1.205倍，在对土样的径向进行测量时，须引入一个修正系数消除折射效应所造成的径向测量误差。

Geiser等[14]建立的折射模型详细的阐明了土样图像变形与相机拍摄方位的关系，当相机机位固定不变、拍摄方向与土样垂直时，土样图像受到的折射影响基本认为是相同的。为了简化折射校正过程，将压力室中的图像测量值与空气中土样的图像测量值的比值作土样的放大倍数，取多个放大倍数的平均值作为土样的修正系数，在进行土样变形的测量时可利用修正系数来得到真正的被测土样尺寸。通过折射修正系数对径向测量值进行修正的绝对测量误差为±0.17 mm，即利用折射修正系数能够有效地减小因折射效应引起的径向测量误差。

3 基于图像测量的红黏土不固结不排水三轴试验

3.1 试验方案

与常规三轴试验不同，本试验将新型图像测量技术运用于红黏土的不固结不排水三轴试验中，根据《土工试验方法标准》GB/T 50123—2019制备三轴土样，土样尺寸为80 mm×39.5 mm，干密度ρ=1.5 g/cm3，含水率w=23%，在不同围压σ3下进行剪切。为了获取土样变形过程中的数字图像，试验采用位移控制式加载方式，剪切速率为0.2 mm/min，通过控制轴向位移进行间歇性加载，当轴向位移依次达到1 mm→2 mm→3 mm…→11 mm→12 mm时，暂停轴向加载；在土样四周设置固定的环形图像采集方位，每一阶段的轴向加载结束后，在图像采集方位处进行土样的数字图像采集，图像采集完毕后再继续以相同的加载速率进行轴向加载，加载到指定位移阶段后再次进行图像采集，直至试验结束。基于图像测量的三轴试验在常规三轴试验的基础上进行，无需对常规三轴试验进行任何的改进，只需要新增一部相机对土样进行图像采集，相机分辨率高，相对较小的编码点也能够在图像中清晰地呈现出来，图像中编码点的几何特征、灰度特征能够被准确地检测。在使用高分辨率相机时，选用尺寸相对较小的编码点，使编码点尽可能多地分布于被摄物体表面。而且在试验时，可同时采用图像测量方法和常规测量方法对土样的变形进行测量。

3.2 试验结果分析

图4是三轴试验剪切过程中土样的变形图像，可以非常直观地了解土样剪切过程中每一个阶段的变形情况。

图4 三轴土样各阶段变形图Fig.4 Deformation diagram of triaxial soil samples at various stages

根据不固结不排水剪切试验的轴向力作用面积的校正计算，得到红黏土不固结不排水剪切的轴向力作用面积，并由此计算得到土样在剪切过程中的径向变形，测量结果详见表4。由于土样两端试样帽、基座端部摩擦力的影响，土样的实际变形是非均匀的，根据校正面积换算得到的径向变形完全不能反映出土样的实际径向变形。

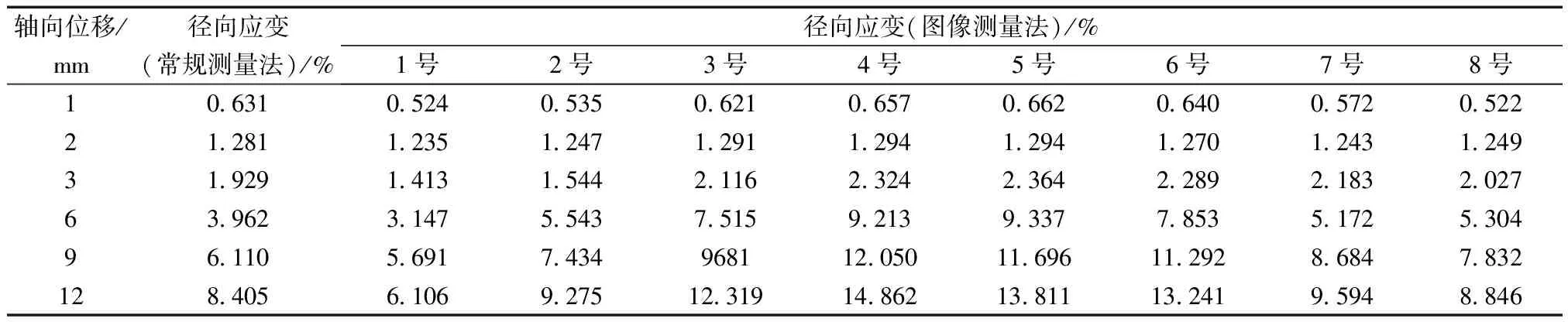
表4 两种方法径向应变测量对比Table 4 Comparison of two methods of radial strain measurement

鉴于土样径向应变并不各向均等，依据实测数据对土样的受力面积进行计算应更为合理。使用PhotoModeler Scanner软件对数字图像中的RAD编码点进行识别，获取编码点在三维空间中的坐标，利用变形土样的三维数字模型获取土样任意部位的径向长度。通过对弧形压力室、水造成的折射影响的探讨可知，折射效应对土样的径向图像测量具有非常大的影响，因此，在进行土样的径向变形计算前，必须按照基于光线追踪的三维折射校正模型对土样表面的所有编码点进行折射校正，得到土样表面编码点的真实三维坐标。根据土样的真实三维坐标重构土样的三维空间模型，从而实现对土样径向变形的测量。在红黏土的不固结不排水三轴试验中，土样的径向测量区域如图5(a)所示，取同一轴向高度附近处编码点云的平面坐标进行平面圆的拟合，获取土样不同轴向截面处的径向变形，如图5(b)所示。对土样不同轴向高度处的径向变形测量截面进行编号，由下至上截面编号为1～8号。

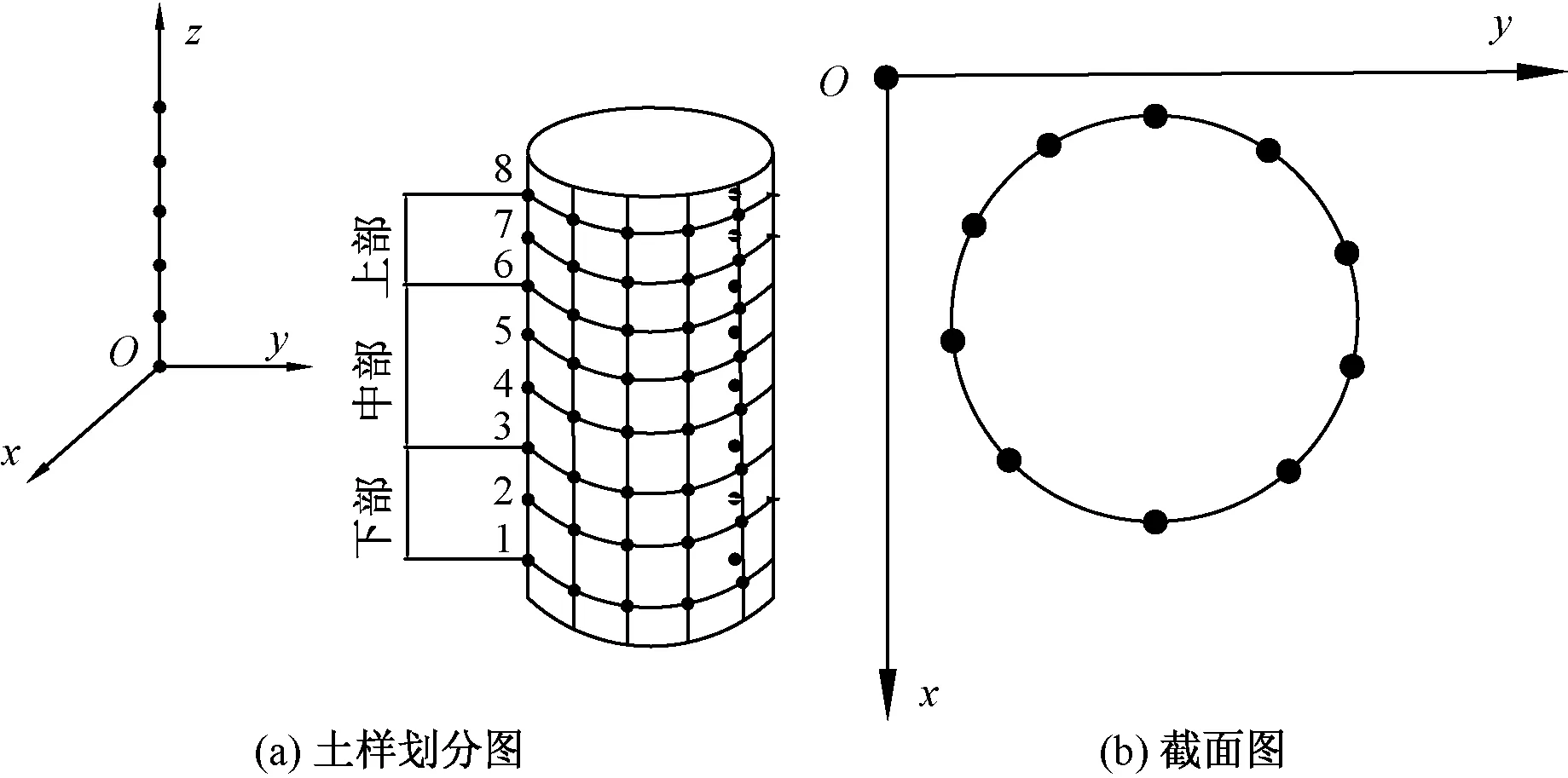
图5 土样截面及土段分布Fig.5 Soil sample cross section and soil section distribution

由表4及图4可知，在轴向加载的初期，源于土样两端受到的轴向压力较小，土样与试样帽、基座接触部位的摩擦力较小，对土样变形的侧向约束效应并不明显，在此阶段可认为土样是均匀体，土体各向均匀变形，土样各部位的横截面直径大致相同。此时，采用常规测量方法换算得到的平均径向变形与图像测量方法所得到的径向变形基本一致，都能较好地反映出土样在压缩过程中的实际变形状态。随着轴向位移的加载，土样端部接触部位的摩擦力逐渐增大，土样的不均匀性导致土样内部出现应力集中，出现不均匀变形。此阶段内的土样不再可视作均匀单元体，端部约束对土样两端的径向变形具有强烈的约束效应，从土样端部至土样中部，端部约束对土样变形的影响明显减弱，土样的径向变形具有一定的对称性，土样中部受到的约束效应较小，该部位的变形更能反映出土样的应力-应变特征。常规测量方法获取的是土样的平均径向变形，随着不均匀变形的加剧，平均径向变形对土样径向变形的定量描述就越失真实性。与常规测量方法相比，图像测量方法可依靠土样的三维数字模型，直接对土样任意径向截面或土样段的径向变形进行测量。

三轴土样所受应力与轴向力的作用面积相关，在常规三轴试验中，鉴于土样的变形是不均匀的，根据实际变形量计算的结果应更为合理，但常规试验中对土样的不均匀变形进行测量是比较困难的[15],所以《土工试验规程》GB/T 50123—2019中采用等应变简化来进行计算，假定土样各部位的径向变形是一致的，这就导致常规三轴试验获取的应力-应变曲线与土样的实际应力-应变关系具有差异。在常规饱和红黏土不排水剪切试验中，运用图像测量方法对土样不同部位的径向变形进行测量，依据实测的土样径向数据确定轴向力的实际作用面积，从而明确土样不同部位实际作用的轴向偏应力，遵循土样的变形特征，在土样的端部和中部选取3个测量截面(截面2、截面4、截面7)分析土样不同变形部位的应力-应变关系曲线，图6为常规测量方法和图像测量方法获取的应力-应变曲线。

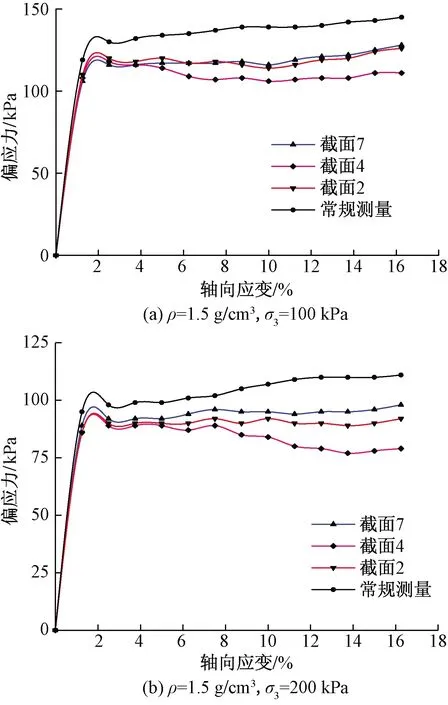
图6 不同截面处的应力-应变曲线Fig.6 Stress-strain curves at different sections

由图6可知，在初始阶段，两种测量方法获取轴向力作用面积基本一致，在该部分两种方法获取的应力-应变曲线基本重合，土样的变形接近于均匀变形，此时土样各部分受力均匀；随着剪切的进行，端部约束对土样两端的变形产生明显的限制作用，土样中部出现明显的鼓状变形。源于对土样受力面积的计算方法不同，在相同轴向应变条件下，两种测量方法测得的应力-应变曲线出现明显的分异[16]。在常规试验中，得到的径向变形是综合了土样端部与中部不均匀变形后的平均径向变形，然而轴向力的作用面积较土样的实际受力面积偏小。依据图像测量结果，截面2、4、7处的实际径向变形都大于常规试验换算得到的径向变形，土样各部位实际承受的轴向应力都小于常规三轴试验换算得到的轴向应力。在土样破坏时，土样实际承受的轴向偏应力要小于常规测量结果，常规测量方法得到的土样强度偏大，这是由于常规试验中是假定土样各部位的径向变形是一致的，而根据土样实际变形图(图4)以及图像测量方法得到的径向测量结果看，径向变形是不均匀的，从而导致轴向力作用面积不一致，又根据应力等于力除以其作用面积可得图像测量得到的偏应力要小。

4 结论

(1)图像测量技术通过被摄物体不同视角下的数字图像重构获取被摄物体的三维空间形态，可实现高精度的物体三维重构，将图像测量技术运用于土样三轴试验中，为土样的变形测量提供了一种更加直观、有效和非接触式的测量方法。

(2)有机玻璃压力室罩和水造成的折射效应对图像测量结果具有比较大的影响，试验结果表明：压力室罩和水折射影响是造成测量误差的两个主要因素，利用修正系数可有效地消除测量误差；折射效应对土样的径向测量具有较大的影响，对轴向测量的影响可忽律不计。

(3)将图像测量技术应用于红黏土的不固结不排水三轴试验中，对土样不同部位的变形量进行测量，对比了图像测量结果与常规测量结果，结果表明：图像测量得到的偏应力要小于常规测量结果，常规测量方法得到的土体强度偏大。