直流馈入影响下交流输电线路的纵联保护方案
2021-10-15刘雨姗李凤婷
刘雨姗, 李凤婷
(新疆大学电气工程学院, 乌鲁木齐 830047)
高压直流输电以传输功率大、线路造价低的优势,在远距离输电和区域互联上得到了广泛的应用,中国已建成世界上最大的交直流混联电网[1-2]。纵联差动保护以快速性强、灵敏度高的优势,作为主保护广泛应用于交流输电系统中[3]。由于交直流系统间的连锁故障特性,若交流系统发生故障导致直流发生换相失败引发交流系统保护误动会对直流系统造成二次冲击,从而影响交直流互联电网的稳定运行。传统交流输电线路纵联差动保护能否适用有待商榷。西北地区拥有“大直流、弱交流”的电网格局,存在交流系统故障引发直流系统稳定的问题[4]。因此,研究准确判别直流馈入影响下的故障判据,完善适用于逆变侧交流架空线路的保护方案,对提高交直流互联电网的运行稳定性具有重要意义。
针对直流馈入对邻近交流线路保护的影响,中外学者进行了大量研究。文献[5]指出交流系统单一故障时具有复故障特征,若直流系统故障产生的附加电源强于交流系统故障附加电源,会导致传统继电保护理论不适用。文献[6]得出直流系统的存在导致故障分量电流差动保护的动作量减少、制动量增加,从而降低保护动作的灵敏性。为解决这个问题,文献[7]利用输电线路两侧电流相位的差异改进传统判据,但所提判据仅通过仿真分析定性得到,且发生经大过渡电阻接地故障时,相角差异不明显,判据存在失效的可能。文献[8]通过提取单相有功电流制定了一种分频有功瞬时基波差流保护方案,该方案不需借助电阻参数且避免了无功补偿电流的影响,但需借助锁相环提取有功电流,电路复杂,调试不便。文献[9]计及直流控制作用的影响下,引入了一个较低的制动系数区间(0, 0.5),提出了基于电流暂降检测的故障分量差流保护判据,提高保护的灵敏性,但判据中引入的新的比例制动系数是通过仿真遍历得到,未给出整定原则。另一方面,也有学者们提出参数识别的方法克服暂态分量的影响。文献[10]提出基于参数识别的纵联保护,将区内外故障模型简化为电感模型,通过比较电感的大小来判别故障,该保护方案在原理上避开了并联电抗器电流的直接计算提高了保护性能,但没有解决不带并联电抗器的交直流混联系统保护误动问题。文献[11]在参数识别的基础上提出了基于阻感模型符合度的判别方法,根据故障相是否符合阻感模型判别故障,该保护方案采用时域全量克服了频率偏移对保护造成的影响,但判据采用修正余弦相似度算法进行阻感模型相关性计算,存在计算烦琐的缺点。综上,目前针对直流馈入影响下电流差动保护拒动问题的研究较少,且均存在整定原理复杂的缺点,本文所提判据不受直流换相失败影响,能够可靠区分区内、区外故障,保护线路全长,且整定原理简单,两种保护方案互相判定提高可靠性,在交直流互联系统里具有一定的优越性。
首先分析直流馈入影响下逆变侧交流输电系统的电气量特征,在此基础上研究直流馈入对交流输电线路电流差动保护动作特性的影响,其次在分析故障模型的基础上对区内、外故障时纵联阻抗表达式进行理论推导,提出基于纵联阻抗幅值与相角的保护方案。最后基于PSCAD仿真软件对所提保护方案进行仿真验证。
1 电流差动保护在交直流混联系统中的适用性分析
传统电流差动保护是反映从被保护元件各对外端口流入该元件的电流之和的一种保护[3],根据采用电气量的不同可分为故障分量判据和稳态量判据,为解决高阻故障下灵敏度不足的问题一般采用故障分量判据。
1.1 电流差动故障分量判据
图1为考虑直流系统的交流输电线路区内故障等值电路图。

Zs1为m侧的等效系统阻抗;Zs2为n侧的等效系统阻抗;Zm为故障点m侧的线路阻抗;Zn为故障点n侧的线路阻抗;Rf为故障电阻;为故障点对地电压;为故障点处形成的故障分量电压源;ΔIdc,f为直流系统馈入故障点的故障分量电流;为故障点处的故障分量电流;为直流系统馈线路m侧的故障分量电流;为直流系统馈线路n侧的故障分量电流;为交流线路上m端母线处的故障分量电流;为交 流线路上n端母线处的故障分量电流图1 直流馈入下交流输电线路区内故障等值电路图Fig.1 Circuit diagram of fault equivalent circuit in AC transmission line area under DC feed
传统的电流差动保护故障分量判据为
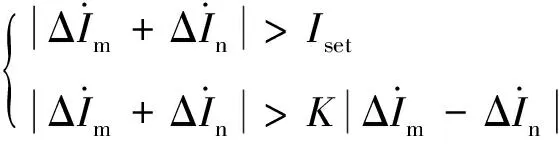
(1)
由图1可知,在不考虑直流系统时,动作量和制动量分别为

(2)
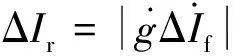
(3)

考虑直流馈入下的动作量和制动量则叠加了直流系统馈入的等值故障分量电流的影响,动作量和制动量分别为

(4)

(5)
1.2 直流馈入对电流差动保护的影响
直流系统对交流系统保护的影响表现在馈入的直流等值电流上,会使故障电流的变化特征不同于纯交流系统,即直流系统的等值故障分量电流超前于故障分量电压呈容性[9]。为说明直流系统注入交流系统等值电流变化的具体情况,现搭建基于国际大电网会议(conference international des grands reseaux electriques,CIGRE)的标准模型的交直流混联系统电磁暂态仿真模型,如图2所示,其中直流电压等级为±500 kV,送受端系统均为230 kV,假设在1 s时区内f点处发生经金属性过渡电阻接地故障,据此分析直流系统等值电流的变化情况。
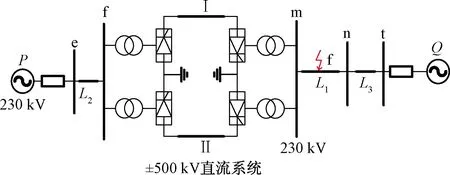
图2 交直流混联系统示意图Fig.2 Schematic diagram of AC/DC hybrid system
图3为考虑直流系统馈入等值电流影响下逆变侧故障分量电流的相位Φ变化情况,其以故障分量电压为参考量。

图3 直流馈入下逆变侧故障分量电流相位变化情况Fig.3 Current phase change of the inverter side fault component under DC feed
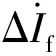
综上,直流系统等值电流的馈入会导致传统电流差动保护动作量减少、制动量增加,从而导致基于工频故障分量的电流差动保护在交直流混联系统中存在适用性问题。
2 直流馈入影响下基于故障模型的纵联阻抗推导
2.1 考虑直流馈入的纵联阻抗
现有研究基于线路两端电气量计算的阻抗构建输电线路的纵联保护,并将这个阻抗定义为纵联阻抗[12-13]。基于图2的交直流混联系统示意图,纵联阻抗Zcd及其相角Φcd可表示为
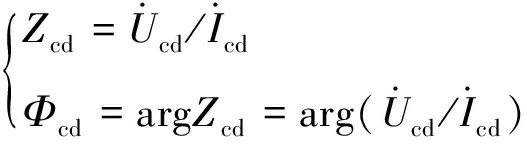
(6)

(7)
式(6)将图2交流输电线路L1两侧保护安装处加入直流影响的差动电压相量与差动电流相量的比值定义为纵联阻抗。为了便于定性地分析输电线路区内、外故障时阻抗相角和幅值的变化特征,下面以单相故障模型为例,推导区内、外故障时纵联阻抗的表达式。
2.2 区外故障时的纵联阻抗
区外故障附加网络等值电路如图4所示,其为考虑直流馈入的交流系统输电线Lmn外部发生故障时故障附加状态网络图,将输电线路等效为π型等效电路,假设线路在区外f点发生故障。

uf为故障点发生扰动时等效的故障电源;ZL为π型等效电路对应的等值阻抗;C为π型等效电路的对地电容; um、im、un、in为流经保护安装处的测得的电压、电流,其值为故障点引起的电压、电流 与直流系统换相失败引起的电压、电流馈入量之和。图4 区外故障附加状态网络Fig.4 Out-of-zone fault additional status network
将电流的正方向设定为从母线流向线路。由图4可知,当发生区外故障时,得
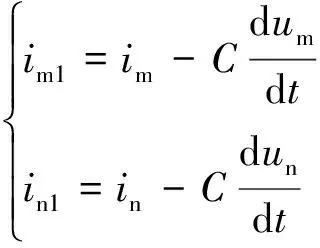
(8)
im1与in1大小相等,方向相反,则
im1+in1=0
(9)
将式(8)、式(9)相加,则

(10)
定义差动电流icd,差动电压ucd为
icd=im+in,ucd=um+un
(11)
当输电线路发生区外故障时,差动电流、电压方程满足关系

(12)
由于线路阻抗远远小于对地容抗,当线路是长线路时,式(12)依旧满足。由式(12)可推出区外故障时故障状态网络对外呈现电容特征,因此可将其等效为一个纯电容电路模型,如图5所示。

图5 区外故障等效电容模型Fig.5 Equivalent capacitance model for out-of-zone faults
由图5可推出区外故障时纵联阻抗的表达式,差动电压与差动电流相量比值为

(13)
式(13)中:ω为角频率,综上分析可知,当线路发生区外故障时,Zcd=ZC,线路两端保护安装处的电压相量和与电流相量和的比值为容抗,具有明显的区外故障特征。
2.3 区内故障时的纵联阻抗
线路发生区内故障时,故障附加网络等值电路如图6所示,假设线路在区内f点发生故障。

图6 区内故障附加状态网络Fig.6 Internal fault additional state network
图6中,icm、icn为流过输电线路的容抗电流,其中,Zm=Rm+jωLm、Zn=Rn+jωLn,假设故障点故障形式为短路电流经过渡电阻Rf接地,则uf=ifRf,if为流经过渡电阻的两端故障电流之和,即if=im1+in1。
由图6可知,当系统发生区内故障时,输电线路m端和n端保护安装处的电压分别满足

(14)
在计算中可近似忽略流过输电线路的容抗电流icm、icn,即im1≈im,in1≈in,假设电流分配系数Km=Zn/(Zm+Zn)、Kn=Zm/(Zm+Zn)。
由式(14)可得
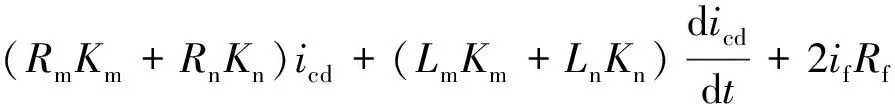
(15)
当发生区内故障时,输电线路两端差动电压、电流满足

(16)
式(16)中:R=RmKm+RnKn;L=LmKm+LnKn。令
R1=R+2Rf
(17)
则式(16)可写为
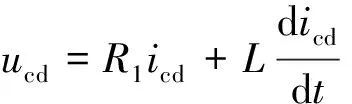
(18)
由式(18)可知,当输电线路发生区内故障时故障状态网络对外呈现阻感特征,因此可将其等效为一个电阻、电感串联的电路模型,如图7所示。

图7 区内故障等效阻感电路Fig.7 Equivalent resistance inductance circuit
由图7可推出区内故障时纵联阻抗的表达式,差动电压与差动电流相量比值为

(19)
综上分析可知,当线路发生区内故障时,Zcd等于ZL,线路两端保护安装处的电压相量和与电流相量和的比值为呈感性的阻抗,具有明显的区内故障特征。
由上述理论推导得,在受邻近直流馈入影响的交流输电线路中,当线路发生区外故障时,输电线路等效为一个电容模型,其纵联阻抗呈容性,Zcd的幅值在理论上等于|ZC|;当线路发生区内故障时,输电线路等效为一个阻感模型,其纵联阻抗呈感性,Zcd的幅值在理论上等于|ZL|。该算法为根据线路两端的电气量反推线路参数的参数识别算法,因此,该算法仅与线路参数本身的大小有关,与交流系统的强弱及潮流水平无关。根据线路上的参数计算可知,区外故障时,纵联阻抗的幅值很大,区内故障时,纵联阻抗幅值很小,据此制定了基于纵联阻抗幅值及相位的判据。
3 基于纵联阻抗的纵联保护方案
3.1 基于纵联阻抗幅值的保护方案
通过纵联阻抗幅值在区内外故障时具有差异性来判别故障,基于纵联阻抗幅值保护的具体判据为
|Zcd| (20) 式(20)中:Zset为整定阻抗值。 当满足式(20)时,说明线路发生区内故障,否则为区外故障。Zset整定原则为 Zset,up=Krel,upZC (21) Zset,low=Krel,lowRTmax (22) (23) 式中:Krel为可靠系数,对于不同的工程要求,定义区间为[0.3,1.0],RTmax为规程规定对应电压等级应考虑的最大过渡电阻,由式(21)~式(23)计算可得,整定值Zset=532 Ω。由于区内故障纵联阻抗的幅值趋近于0,因此该判据具有足够的安全性,能够准确快速的区分区内外故障,不会造成保护的误动或拒动。 通过上述关于交直流故障模型的理论分析可知,纵联阻抗的相角在区内外故障时具有明显差异性,区外呈容性,区内呈感性。因此,基于纵联阻抗相位的判据可表示为 Φcd>Φset (24) 当满足式(24)时,说明线路发生区内故障,否则为区外故障。Φset为整定相角值,其整定原则为 Φset=KrelΦC (25) 当故障为区外时,阻抗角非常接近-90°,经式(25)计算得,整定值Φset=-45°。无论故障位置发生在何处,区外故障时,纵联阻抗的相角始终小于0,区内故障时,纵联阻抗的相角始终大于0,因此该保护判据能够可靠动作。将整定值设为-45°,对于高过渡电阻的故障具有较高的灵敏度,减小了高过渡电阻故障时扰动引发的误动可能性。 所提的保护方案不采用线路两端电流求和的方式判别故障,从保护判据上避免了直流系统等值电流的影响,能够有效解决基于工频故障分量的电流差动保护在交直流混联系统中存在适用性的问题。 运用PSCAD/EMTD仿真软件搭建了基于CIGRE的标准模型的交直流混联系统电磁暂态仿真模型,如图2所示;其中±500 kV的高压直流输电系统(high voltage direct current,HVDC)经单回交流输电线路馈入受端交流系统为230 kV的交流电网中;交流系统由两段单回输电线路组成,线路mn的长度为400 km,线路nt 的长度为40 km;保护装置的采样频率为4 kHz,线路单位正序和零序的电阻、电抗、容抗分别为r1=0.017 8 Ω/km、x1=0.313 Ω/km、xc1=273.545 Ω·m、r0=0.295 Ω/km、x0=1.03 Ω/km、xc0=414.164 Ω·m。为研究直流馈入的影响,设与直流系统直接相连的输电线路mn为区内,则线路nt为区外。以A相仿真结果为例,对交直流混联系统交流侧线路发生单相接地故障时电流差动保护进行仿真验证。 为分析传统故障分量差动保护在交直流互联系统里的性能,在线路mn距离m端50 km处分别设置区内A相接地故障、AB两相接地故障,故障发生时刻为1 s,持续时间为0.1 s,过渡电阻分别取50、100、200 Ω,前两个过渡电阻值会造成直流系统换相失败,由于在0~20 ms这一时段采用全周傅氏算法的故障分量差动保护还未启动,故从1.02 s开始记录数据。根据ΔId/ΔIf与制动系数K的大小关系来分析保护动作情况,仿真结果如图8所示。 图8 传统故障分量差动保护动作情况仿真结果Fig.8 Simulation results of traditional fault component differential protection 由图8可知,在故障时段内,在线路发生A相接地故障下,当过渡电阻为50 Ω时,A相差动电流与制动电流的幅值比在制动系数区间内,始终大于制动系数下限0.5,传统故障分量差动保护能够可靠动作;当过渡电阻为100 Ω时,ΔId/ΔIf在制动系数下限0.5附近,判据存在拒动的可能;当过渡电阻为200 Ω时,ΔId/ΔIf持续低于0.5,传统故障分量差动保护判据失效。对于两相接地故障,与单相接地故障保护动作情况类似,经大过渡电阻接地下保护判据可能出现拒动。综上,在交直流互联系统中传统故障分量电流差动保护抗过渡电阻能力差,大过渡电阻时判据存在拒动的可能。 4.2.1 基于纵联阻抗幅值的保护方案仿真验证 为验证所提保护方案在发生逆变侧交流故障时的可靠性,计及不同故障类型和不同故障位置这两个影响因素,在模型mt线路段分别设置区内、区外故障,将故障类型分别设置为A相接地故障、AB相间故障,发生故障处为线路出口、中点及末端处,故障发生时刻为0.9 s,持续时间为0.3 s,以发生金属性接地故障为例,设置过渡电阻为0的故障,此时将导致直流系统发生换相失败,结合式(20)对基于纵联阻抗幅值的纵联保护方案进行仿真分析,验证其是否能正确识别故障,仿真结果如图9所示。 图9 基于纵联阻抗幅值的判别结果Fig.9 Judgment result based on the amplitude of longitudinal impedance 从图9可以看出,当线路在0.9 s发生区内故障时,故障相的纵联阻抗幅值瞬间下降至数十欧,趋近于0,故障清除后,阻抗值恢复正常。当发生区外故障时,纵联阻抗的幅值大于1 000 Ω,与区内故障阻抗值趋近于0的特征差异明显。发生故障后,区内纵联阻抗幅值远小于整定阻抗值,区外纵联阻抗幅值远大于整定阻抗值,即当纵联阻抗的幅值小于532 Ω时,必为区内故障,线路两侧保护同时动作,否则处在保护判据式(20)的动作选择区域外,保护可靠不动。仿真结果与3.1节分析一致,说明所提判据不受换相失败的影响,能够可靠识别区内、区外故障。 4.2.2 基于纵联阻抗相位的保护方案仿真验证 工况、参数条件设定同4.2.1节,依旧以金属性接地故障为例,结合式(24)对基于纵联阻抗相位的保护方案进行仿真分析,验证当直流发生换相失败时,以及受不同故障类型和不同故障位置影响时,所提判据是否能正确识别故障,仿真结果如图10所示。 图10 基于纵联阻抗相位的判别结果Fig.10 Judgment result based on longitudinal impedance phase 从图10可以看出,当线路在0.9 s发生区内故障时,故障相纵联阻抗的相位明显的从容性变为感性,当发生区外故障时,纵联阻抗呈容性,相角在-90°上下波动,远小于设定的整定相位Φset。可见,当纵联阻抗的相角大于-45°时,必为区内故障,线路两侧保护同时动作,否则处在保护判据式(24)的动作选择区域外,保护可靠不动。仿真结果与3.2节分析一致,说明所提判据不受换相失败的影响,能够可靠识别区内、区外故障。 为进一步验证所提保护方案在交直流混联系统中的性能,本节在线路首端处设置单相经过渡电阻接地故障,分别对两个判据的抗过渡电阻能力进行仿真验证,并与4.1节的实验结果进行对比证明所提判据的优越性,其中基于纵联阻抗幅值的抗过渡电阻能力仿真结果如图11所示。 图11 基于纵联阻抗幅值抗过渡电阻能力仿真Fig.11 Simulation of anti-transition resistance ability based on longitudinal impedance amplitude 从图11可以看出,当线路上发生带过渡电阻故障时,保护仍能可靠的动作,具有较好的抗过渡电阻能力。但对于故障相A相发生经大过渡电阻区内故障时,纵联阻抗的幅值会有较大变化,此时可采用基于纵联阻抗相位的保护判据联合判定故障,使保护可靠动作。 将同样参数设置在基于纵联阻抗相位判据的抗过渡电阻能力仿真分析中,具体仿真结果如图12所示。 图12 基于纵联阻抗相位抗过渡电阻能力仿真Fig.12 Simulation of anti-transition resistance capability based on longitudinal impedance phase 从图12可以看出,当交流输电线路区内经大电阻接地故障时,交流输电线路纵联阻抗相角跌落较大,但相角门槛值仍留有一定裕度,区外故障时,无论过渡电阻多大,相角均稳定在-90°附近。因此,当线路上发生带过渡电阻故障时,基于纵联阻抗相位的保护判据仍能可靠的动作。 由4.3节与4.1节的过渡电阻对保护方案影响的仿真结果对比可知,传统故障分量差动保护在过渡电阻为100 Ω时就已出现拒动的情况,基于纵联阻抗幅值及相位的保护在过渡电阻为200 Ω时依然留有一定的裕度,故本文所提基于纵联阻抗的保护判据较传统故障分量电流差动保护判据可靠性高,抗过渡电阻能力强,且整定原理简单,具有优越性。 提出了适用于受邻近直流馈入影响的交流输电线路纵联保护方案。首先通过分析直流馈入影响下交流输电线路区内外故障时的故障模型,推导建立了区内外纵联阻抗的表达式。其次根据纵联阻抗幅值及相角在区内外故障时呈现的差异,提出了基于纵联阻抗幅值及相角的保护方案,两种保护方案互相判定,使基于纵联阻抗的保护方案更加严谨。最后利用PSCAD/EMTD仿真软件搭建了交直流混联系统电磁暂态模型对所提判据进行仿真验证,仿真结果表明了所提判据能够快速、有效的区分内部与外部故障,不受电容电流的影响可用于不带并联电抗器的交直流混联系统,减小了直流馈入对电流差动保护的影响,且具有良好的抗过渡电阻能力。以上研究内容主要在不同故障类型、不同故障位置、不同过渡电阻下对保护判据进行了仿真分析验证其可靠性,在后续研究中将关注所研究成果在实际应用中的发展。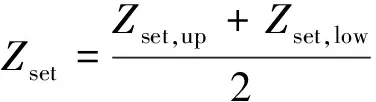
3.2 基于纵联阻抗相位的保护方案
4 仿真验证
4.1 传统故障分量差动保护仿真分析

4.2 直流馈入影响下的交流线路纵联保护方案仿真验证


4.3 过渡电阻对保护方案的影响分析


5 结论
