基于小波分析及活动轮廓模型的图像分割方法
2021-10-15冯宇翔
赵 俊,冯宇翔,赵 骥
(1.中钢科技发展有限公司 运营管理部,北京 100080;2.辽宁科技大学 计算机科学与工程学院,辽宁 鞍山 114051)
图像分割的应用范围广泛,但是,它的应用仍存在很多技术难点,尤其是对于有复杂噪声、边界模糊和不均匀图像的边缘提取面临着挑战[1-2]。图像分割方法包括基于区域的方法、基于边缘的方法、基于小波变换的方法、基于统计学的方法、基于分形的方法和基于数学形态学的方法等[3-4]。小波变换最早应用于地震数据压缩中,后在图像处理中也取得了非常好的效果。图像边缘通常对应高频信息,使用小波变换能够有效检测图像边缘,并且具有较好的边缘定位性质。但由于一些特定图像本身的复杂性和多样性,仅仅使用其中的一种方法都很难精准地提取出边缘。因此,在实践中通常融合多种方法。本文通过小波变换计算不同尺度下的模值和相角值来重新定义图像的边缘轮廓,并通过水平集方法进行迭代收敛。与传统的GAC(Geodesic active contour)模 型、CV(Chan-Vese)模型、GVF(Gradient vector flow)模型等分割方法相比,小波分析方法能够精准地提取出边界区域,对噪声有很好的鲁棒性[5-6]。本文利用小波模极大值方法的特性,将其应用于图像分割,提出了一种基于小波分析和活动轮廓模型[7-8]的图像分割方法。
1 小波多尺度分析
小波变换利用ψa,b(t)作为基底函数,对处理的信号f(x)分解
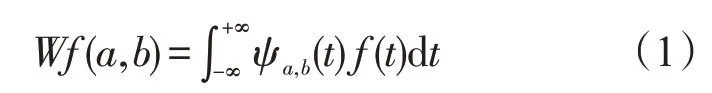
经过平移和伸缩后得到小波系列
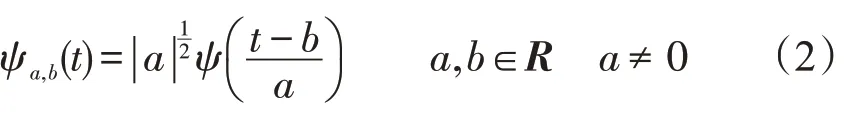
式中:ψ为基小波;a为伸缩因子;b为平移因子。
积分变换生成了一个以a为尺度参数的尺度空间,参数a越大,输出信号中的高频成分越少,即信号的细节信息越少。由于小波分析中强调的是信号分解后的可完全重构性质,因而要求基函数满足Riesz条件和二尺度关系[9]。一般生成尺度空间的变换算子不局限于线性积分变换,曲线演化的偏微分方程都可以生成以演化时间t为尺度因子的尺度空间。
通常一个二维的Gabor滤波器组[10]在[0,π]范围内设计8个角度的通道,同一角度下的通道数为4。由于图像中有不同的频率区,当某一滤波器的频带范围和取向正好与图像中的一种频率相匹配时,则图像中的这一频率区域将有较强的响应,在滤波器组的多通道输出中可能比原始图像中的差别更加明显。和基于区域或基于边缘的分割方法结合起来,可以提高对目标区域的分割效果。
2 二维小波多尺度边缘检测
小波边缘检测先平滑图像信号,再由平滑后信号的一阶或二阶导数来检测出原始信号的突变点(即边缘)[11]。

其中Ψ1(x,y)和Ψ2(x,y)具有小波的完备性和稳定性,选取二者为基母函数,取尺度函数s=2j,则

在x和y方向的定义小波变换系数为
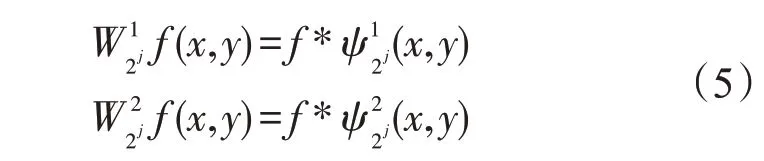
则图像f(x,y)的小波变换为
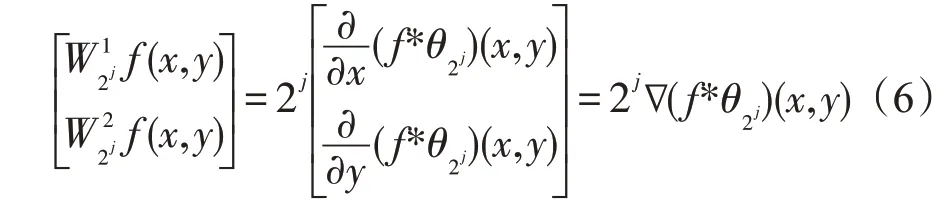

小波变换的模正比于梯度向量的值,图像经过平滑后,其图像的拐点处与矢量A2jf(x,y)方向上M2jf(x,y)的局部模极大值是一致的,也就是说,找到了梯度方向上的模极大值就找到了图像的边缘。
3 活动轮廓模型
活动轮廓模型是一种典型的偏微分方程方法[13-14],将界面看成零水平集,位于高一维空间,列出满足水平集函数的发展方程,通过求解方程推进函数演化,如图1所示。

图1 水平集演示Fig.1 Illustration of level set
不规则阴影部分是水平集演化的目标区域轮廓,立体形状是水平集,立体形状上方的矩形截面是对应目标区域的零水平集。不规则阴影部分可以隐式表示为立体形状的某一水平切面,不规则阴影的边缘封闭曲线看作是立体形状ϕ=ϕ(x,y)与矩形截面ϕ=c的相交线

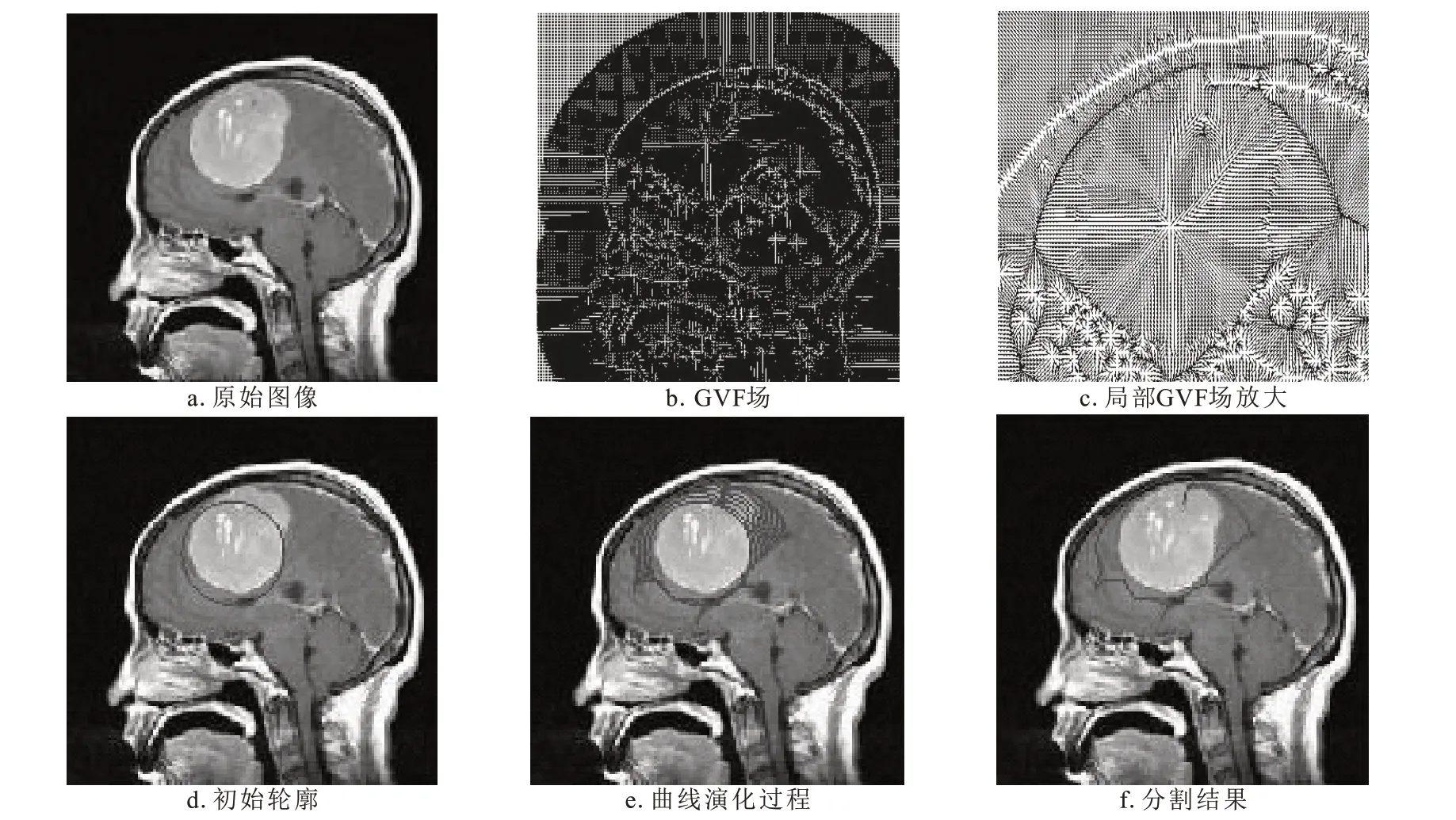
其中,ϕ(x,y)>c时在C外部,ϕ(x,y) 为了方便计算,必须要选择一个恰当的水平集的嵌入函数ϕ(x,y),初始值ϕ0(x,y)与给定的曲线C0相对应,使得ϕ0(x,y)=C0,用由C0生成的符号距离函数来表示ϕ0(x,y)。而水平集嵌入函数ϕ(x,y)的选择具有不确定性,通常会选取平面(x,y)上到C的符号距离函数,可以表示为 式中:d[(x,y),C]表示点(x,y)与曲线C之间的欧式(Euclidean)距离。 在欧式距离中,嵌入函数的梯度 ||∇ϕ≡1,代表水平集的嵌入函数ϕ(x,y)的变化率在每一个(x,y)处都是均匀的,处处光滑。因此,水平集嵌入函数ϕ(x,y)的初始化问题就变成了在一个确定的区域Ω内,计算网格点(x,y)到C0的距离,再根据式(10)赋予距离正号或者是负号。当C0是以点(x0,y0)为圆心,半径为R的圆时,ϕ(x,y)可以初始化为;但当C0不规则时,ϕ(x,y)的初始化就需要计算每一点(x,y)到C0各点的距离,并求出各点距离的最小值。 确定了初始化水平集函数之后,曲线将受到图像力作用促使其发生形变,利用图像中的嵌入函数梯度作为图像力驱动曲线靠近边缘。这个图像力在远离边缘时大,靠近边缘时缩小,直到贴合边缘,达到紧靠轮廓状态,此时停止演化。 本文算法的具体实现流程如图2所示。首先对输入的图像进行小波分解,其次对其边缘点进行检测和计算,最后根据上述结果使用活动轮廓变形模型对图像进行分割。 图2 改进算法流程图Fig.2 Flow chart of improved algorithm 图3的飞机图片中加入了2%的盐椒噪声和10%的高斯噪声。图3a是采用传统GAC模型的分割过程和结果,时间步长τ=0.1,速度常数c=+1,迭代1 500次。由于噪声的影响,弱化了飞机轮廓的边缘,演化曲线穿过了图像的边缘,导致演化失败。 图3b是演化曲线在小波边缘空间的分割过程和结果,其中尺度因子s=1,速度常数c=+0.2。 图3c是演化曲线在小波边缘空间的引导下在灰度图像空间的分割过程和分割结果,其中速度常数c=+1,时间步长τ=0.1,迭代230次。演化曲线定位在飞机的轮廓边缘,表明将小波分析的方法引入到GAC活动轮廓模型中,不仅能够有效加快算法的演化速度;同时还能够加强对噪声的鲁棒性。 图3 基于小波分析的GAC模型的分割过程和结果Fig.3 Segmentation process and results using GAC model based on wavelet analysis 图4a是来自于OASIS大脑MRI数据集的脑部图像[15],通过图像分割可以对病灶进行准确的定位和测量分析。图4d~图4f是演化曲线在梯度矢量流场的驱动下的演化过程和结果。其中GVF模型参数设定为α=0.05,β=0,μ=0.2,由于脑部的结构比较复杂,演化曲线易受到附近梯度矢量场的吸引而偏离目标,最终分割失败。 图4 GVF模型的初始轮廓、分割过程和分割结果Fig.4 Initial contour,segmentation process,and segmentation results of GVF model 图5是演化曲线在基于小波分析的梯度矢量流场的驱动下的演化过程和结果。其中尺度因子s=2,域值c=0.2。经过小波变换后,目标轮廓附近的干扰梯度矢量流被过滤掉,梯度矢量流场被净化和突出。曲线在新的梯度矢量场的引导下可以稳定准确地演化到目标边缘。 图5 基于小波分析的GVF演化曲线的初始轮廓、分割过程和分割结果Fig.5 Initial contour,segmentation process,and segmentation results of evolving curves of GVF model based on wavelet analysis 本文算法实验硬件环境是Intel(R)Corei5CPU,4G内存,采用Windows 7操作系统下Matlab 2014b进行仿真。 采用误分率(Misclassification error,ME)作为指标评价算法。当ME=0时,表明分割结果一致。本文选取91张来自于OASIS大脑MRI数据集的脑部图片进行对比实验。对比传统算法以及本文算法的分割结果:GVF模型的误分率最高,为0.643 1;传统GAC模型误分率降低了近一半,为0.391 2;本文采用的基于小波多尺度模极大值的GAC模型方法误分率最低,达到0.111 3,不到传统GAC模型的1/3。表明本文方法在模糊或渐进边缘分割上取得了更好的成果。 针对传统的活动轮廓模型对噪声比较敏感的缺陷和小波具有多尺度边缘检测的特性,将小波多尺度模极大值边缘检测的思想引入到基于边缘的GAC变形模型和基于参数的GVF模型中,引导演化曲线快速准确地对目标进行分割。实验表明,基于融合小波分析的活动轮廓模型方法,能够有效改善模型的分割效率。提高了边缘提取的准确度和对噪声的鲁棒性。
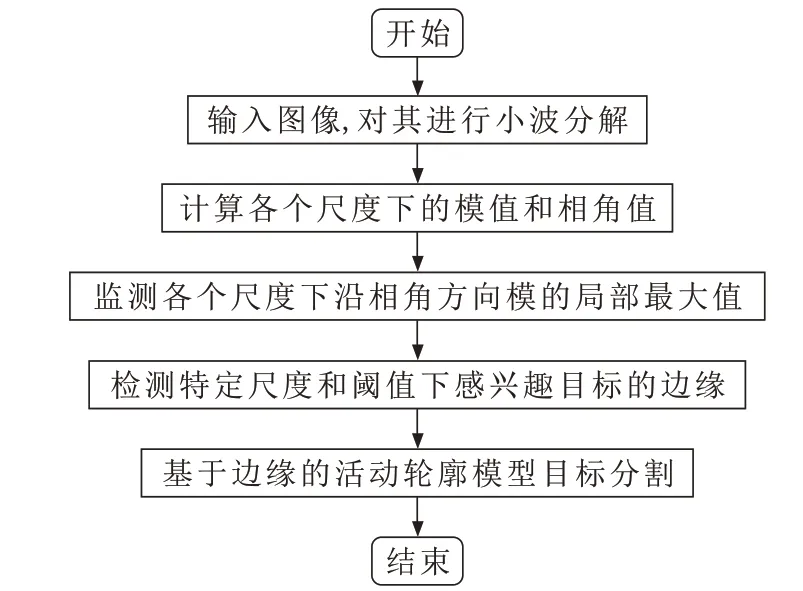
4 实验结果与分析
4.1 小波分析与GAC模型

4.2 小波分析与GVF-Snake模型

5结论
