基于多目标优化的自组织无人机集群航迹规划方法
2021-10-15王原邢立宁陈盈果赵翔黄魁华
王原 邢立宁 陈盈果 赵翔 黄魁华
1.国防科技大学系统工程学院湖南长沙410073
无人机集群(UAV swarm)[1]是由多无人机系统(multi UAV system)发展而来的一种多无人机协同模式.该模式为多无人机系统的高阶形态.相比于一般的多无人机系统,无人机集群呈现规模大、协同等级高、协同过程人工干预少等显著特征[2].采用无人机集群进行空间信息采集,能够有效降低任务的执行成本,且增加可处理任务的复杂性.
自组织无人机集群(self-organized UAV swarm)构架是无人机集群的一种高阶形态.在自组织无人机集群中,无人机个体通过与环境及其他无人机个体的交互进行自主决策,从而使整个无人机集群在任务执行的过程中保持整体性并共同解决复杂任务.因此,自组织无人机集群是一种“集群涌现式智能”[3].
基于虚拟物理规则(virtual physical law)的自组织无人机集群航迹规划方法是一种在现实中具有广泛应用的方法.该方法首次被提出于文献[4].该文献提出了一种基于人工势力场(artificia potential field APF)的无人机集群航迹规划模型.在该模型中,无人机集群中的个体的行动由两种不同的力决定:来自目标的定向力以及来自可探测范围内的个体或其他障碍物的斥力.基于虚拟物理规则的无人机航迹规划方法的主要优势有[5]:
1)能够通过简单地扩展规则使无人机集群具有应对复杂多变环境的能力.
2)无人机的个体行为能够通过简单计算获得.
3)能够使用通用理论工具对无人机集群的行为进行量化分析.
以此为基础,该领域研究者针对基于虚拟物理规则的自组织无人机集群航迹规划问题进行了大量的研究.其中,文献[6] 提出了速度障碍(velocity obstacle,VO)规则.文献[7] 将速度障碍规则进一步扩展为虚拟群组速度障碍(virtual group velocity obstacle,VGVO)规则.该规则保证了无人机集群在分散为多个子集群的同时仍能够较好的完成避障任务.文献[8]将不同无人机以及物体运动的相对速度纳入了虚拟物理规则系统.文献[9]在上文所述规则的基础上提出了一种一般化的无人机集群控制模型,该模型能够广泛适用于不同的无人机编队维持任务并支持自组织无人机集群规模的动态扩展.文献[10]提出了一种集群中存在通讯枢纽的基于Vicesk 模型的无人机集群控制模型,该模型在存在通讯枢纽的无人机集群中能够获得更好地运动一致性表现.
为提升控制模型在不同环境下表现的稳定性,一类重要手段是采用自适应可变参数.针对可变参数的自组织无人机集群控制系统最早由文献[11]提出.该系统由一个包含可变参数的无人机集群控制模型以及用于求解模型参数的进化算法组成.文献[12] 探讨了不同类型的优化算法求解无人机集群控制模型参数的效果,并证明了采用粒子群算法比遗传算法具有更好地优化表现.文献[13]在经典Vicsek 控制模型的基础上增加了可变参数控制集,用于处理无人机集群的聚合任务.文献[14] 采用无人机可变参数控制模型解决了分布式无人机集群的聚合任务,该方法在不同规模的无人机集群环境下均具有良好表现.文献[15]提出了一种包含11 个可变参数的无人机集群控制模型.该模型还研究了无人机存在加速度限制条件下的控制模型的优化问题.
为解决无人机集群可变参数控制模型在多任务环境下的控制效能问题,提出了一种基于规则库的无人机集群控制模型,并给出基于多目标优化方法的无人机集群控制模型参数优化方法.最终,设计多个不同的仿真场景证明该模型的有效性.
1 自组织无人机集群控制模型
介绍基于规则库的无人机集群控制模型(rule based swarm control Model with tunable parameters,RSCMTP).
1.1 基本假设
针对RSCMTP 模型,存在如下基本假设:
针对无人机个体的假设:
1)集群中不存在领导者角色的无人机,集群中无人机个体的行为完全通过个体与周边环境的信息交互自主决定.
2)集群中的个体在任务执行的过程中除了目标点位置信息外不需要接收来自指挥控制系统的其他指令.
3)无人机个体有最大速度限制.
4)无人机个体的探测范围和通讯范围均有限.
5)无人机间的通讯存在延迟.
针对环境的假设如下:
1)无人机集群的任务是穿过任务区域到达指定目标位置,过程中的任务主要涉及避障、队形保持以及到达中间目标点.
2)无人机集群中的个体不应触碰任务区域边界,飞出任务区域边界视为个体死亡.
3)无人机个体不应与障碍物或其他个体发生碰撞,发生碰撞则视为个体死亡.
1.2 无人机速度更新规则
结合环境假设1 可知,该自组织无人机集群的任务主要包括避障任务和目标定向任务.同时,需要保证无人机集群能够维持密集队形.其中,维持密集队形的主要原因是为了维持自组织无人机集群中个体间通讯的畅通.图1 展示了维持密集队形的必要性.
RSCMTP 模型包括3 部分基本控制要素:对目标导航的导航力,避免无人机个体与障碍物碰撞和飞出场地边界的避障力,以及保证无人机集群编队队形的队形维持力.以上3 个力可通过图2 表示.
图2 中,目标位置由无人机集群指挥控制中心输入,队形维持力和避障力则通过无人机个体与环境的交互获得,具体如图3所示.
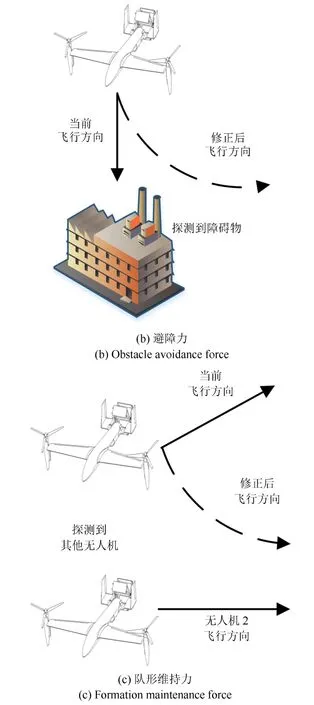
图2 3 种力的作用Fig.2 Three forces
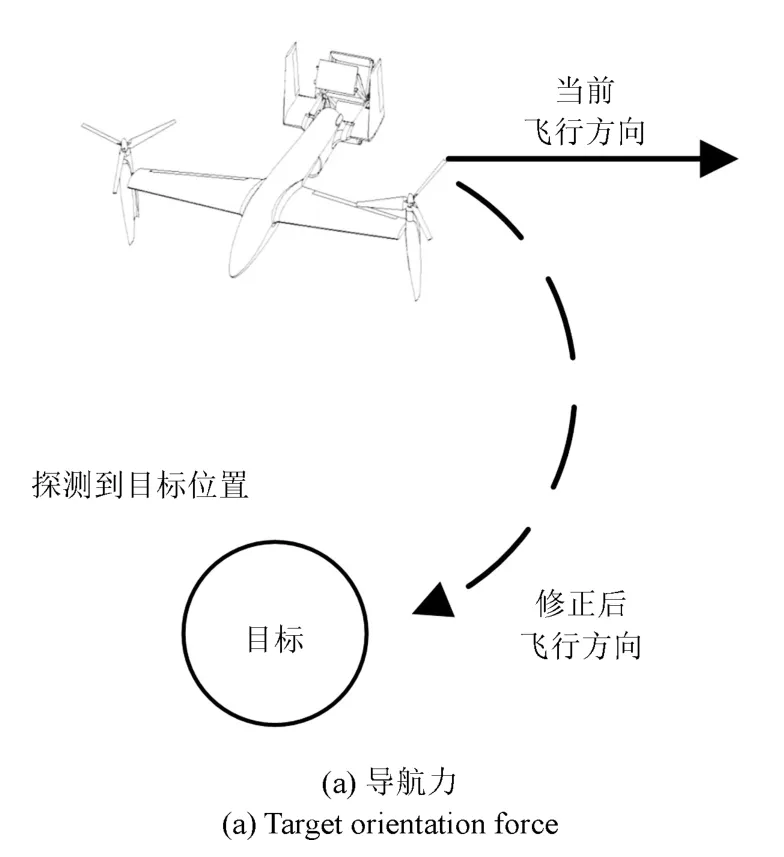
图3 中,当无人机个体在R3范围内探测到存在障碍时,会在可探测到的障碍物表面产生虚拟个体,虚拟个体会向该无人机个体发出避障力以阻止无人机个体继续向该虚拟个体方向移动.当无人机个体探测到其探测范围R0,R1,R2内存在其他无人机时,该范围内的无人机分别向当前无人机个体施加斥力、同向力和引力,以上3 种力的合力被称为队形维持力.在RSCMTP 模型中,设定R0= 1/3R3,R1= 2/3R3,R2=R3.下面分别对所述的力对应的速度更新规则进行介绍.

图3 无人机个体环境交互原则Fig.3 Detection rules of UAV individual
1.2.1 导航力
导航力是指引导无人机个体向当前目标区域飞行的力.导航力可通过式(1)描述.
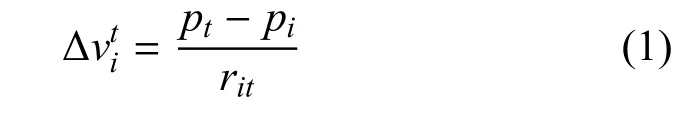
其中,∆vti为个体i受到的导航力,pt和pi分别为用向量表示的目标区域和无人机个体所处的空间位置,rit为目标区域距离当前无人机的距离.
1.2.2 避障力
避障力是为避免无人机个体和任务区域边界或任务区域内可能存在的障碍物碰撞而产生的力.避障力可通过式(2)描述.
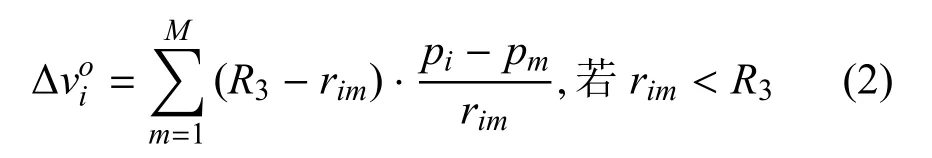
1.2.3 队形维持力
队形维持力的主要作用为维持无人机集群的编队构型.队形维持力由斥力、同向力和引力3 部分构成.以下分别对这3 种力进行介绍.
1)斥力.斥力是保证无人机个体之间不发生碰撞的力.斥力可通过式(3)描述.
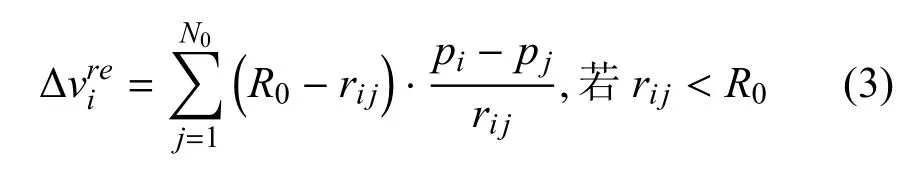
2)同向力.同向力的作用是维持无人机个体之间运动方向和速度的一致性.同向力通过式(4)描述.
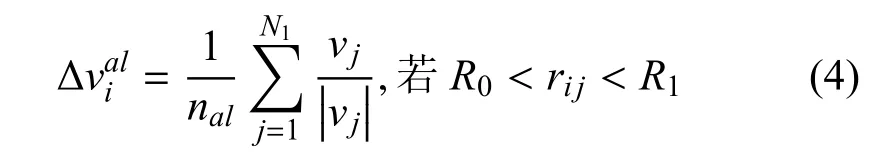
3)引力.引力的作用是维持无人机个体间的距离不超过其探测范围.引力可通过式(5)描述.
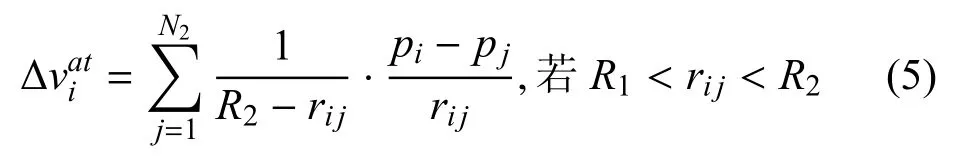
1.2.4 速度更新规则
通过上述描述,最终可得受到3 种力影响的无人机个体的速度更新规则如式(6)所示.
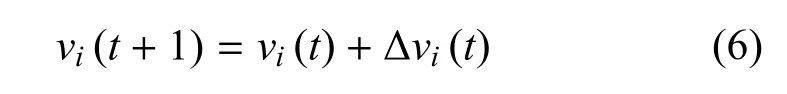
其中,vi(t)为个体i在时刻t的速度,∆vi(t)为个体i在时刻t受到3 种力的影响产生的速度的增量,∆vi(t)可通过式(7)求得.
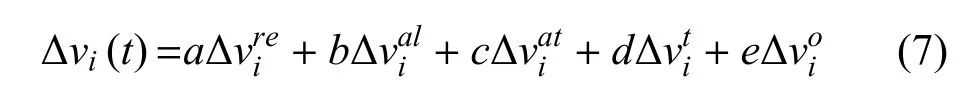
式(7)中,{a,b,c,d,e} 为5 个可变参数,代表不同力在时刻t对速度增量∆vi(t)影响的重要性程度.全部{a,b,c,d,e}5 个参数的取值范围均为[0,1].
1.3 速度更新规则系统
在第1.2 节所述速度更新规则的基础上,RSCMTP 模型还包含一个速度更新规则系统.该系统的主要特征是在速度更新规则的基础上,通过无人机个体探测到的环境信息的不同,采用不同的速度更新规则对无人机的速度进行更新,从而增强了无人机个体的环境适应能力.式(8)介绍了该规则系统中的主要规则.
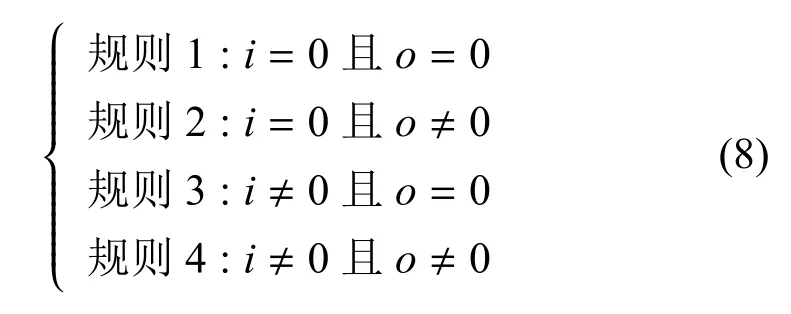
式(8)中,i为无人机探测范围内其他无人机的数量,o为无人机探测范围内障碍物的数量.通过式(8)可得最终的无人机个体速度更新规则如式(9).
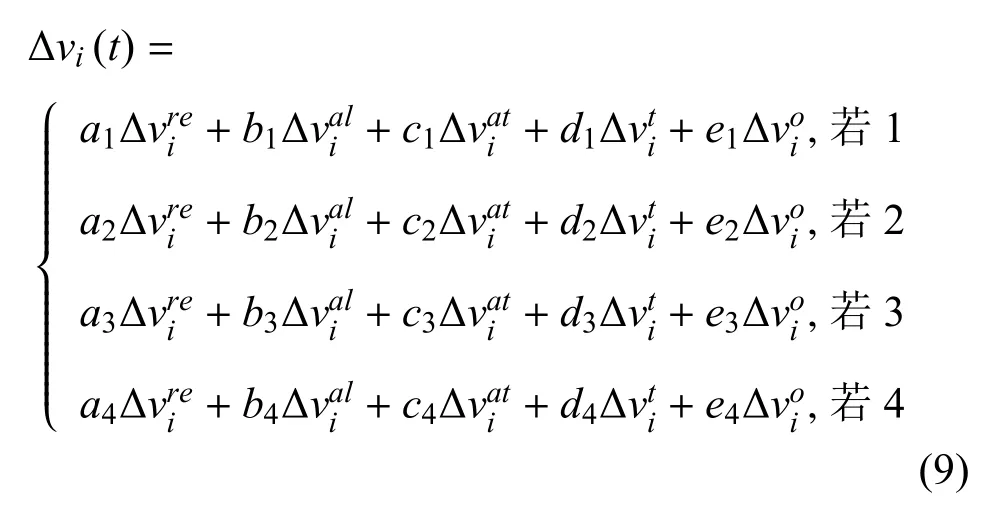
另外需要指出的是,由于无人机个体的速度存在上限,因此,最终的速度更新公式为式(1).

其中,vmax为无人机个体的速度上限.
2 NSGAIII 多目标优化算法
为求解式(9)所述的RSCMTP 模型参数,采用基于NSGAIII[16]的多目标优化算法.该算法是NSGAII[17]多目标优化算法的改进,其在求解多目标优化问题时具有比NSGAII 算法更好的种群多样性表现.以下介绍求解RSCMTP 模型参数的NSGAIII 算法流程.
2.1 编码
用于求解RSCMTP 模型参数的NSGAIII 算法的染色体采取一维顺序编码,该编码方式可通过图4表示.
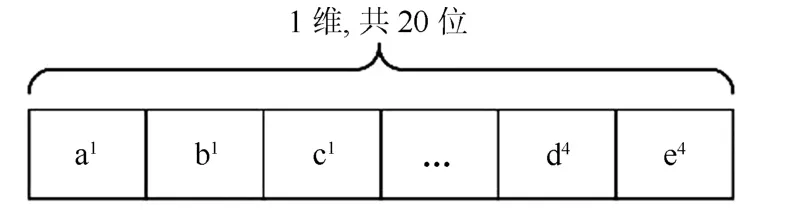
图4 编码Fig.4 Problem encoding
2.2 交叉
NSGAIII 算法中,采用随机交叉算子进行染色体的交叉,具体是指:NSGAIII 算法随机选择父代染色体上最多5 个基因位,并将两条父代染色体上对应的基因位上的参数进行交换.随机交叉算子的具体操作如图5所示.
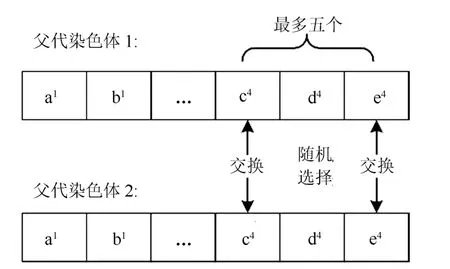
图5 随机交叉算子Fig.5 Random crossover operator
需要额外指出的是,父代染色体的选择采用轮盘赌算法.
2.3 变异
NSGAIII 算法中,采用随机变异算子进行染色体的变异操作,具体是指:NSGAIII 算法随机选择父代染色体上最多3 个基因位,并在参数范围[0,1]内对这些基因位进行重新赋值.随机变异算子的具体操作如图6所示.
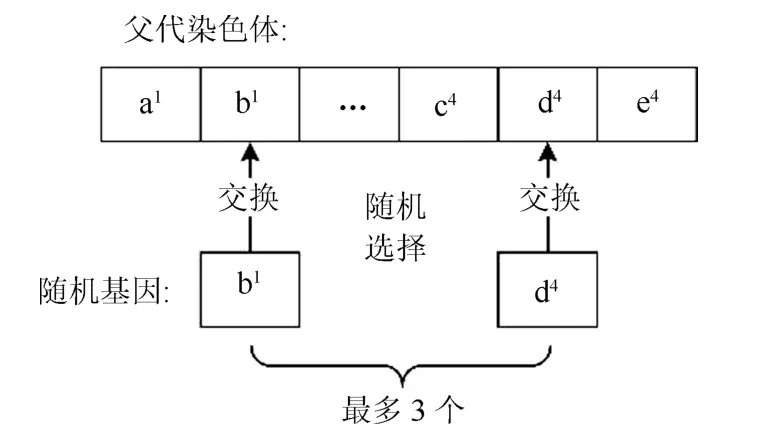
图6 随机变异算子Fig.6 Random mutation operator
2.4 选择
NSGAIII 算法采用基于非支配排序的方式进行下一代种群的选择.设第t代种群为pot,则若要产生种群pot+1,需遵循如下步骤:
步骤1.对pot中的染色体进行评估,并赋予每个染色体非支配排序值,非支配排序值通过支配该染色体的染色体数量决定.例如,设当前染色体i被pot中的2 个其他染色体支配,则染色体i的非支配排序值为2.
步骤2.按非支配排序值从小到大的顺序依次将具有相同非支配排序值的pot中的染色体加入pot+1,直到pot+1中的染色体数量达到或超过种群规模上限.
步骤3.若pot+1中的染色体超过种群规模上限则将pot+1中拥挤度较大的染色体移出pot+1,直到pot+1中的染色体数量等于拥挤度的具体计算方式见文献[18].
染色体质量主要通过以下3 个指标进行评价:
1)死亡率:死亡率用于评价自组织无人机集群中的个体和其他个体,以及环境中的障碍发生碰撞或者飞出任务区域边界的概率.死亡率可通过式(11)计算.

其中,dr为死亡率,D死亡无人机个体数,S N为无人机集群规模.
2)任务完成时间.任务完成时间指标用于评价无人机集群中的个体到达目标区域所需要的时间.任务完成时间可用式(12)计算.

3)聚集指标.聚集指标是指无人机集群维持队形的能力,该指标通过计算仿真过程中无人机集群中的个体距离集群虚拟中心的距离均值得出.为计算聚集指标,需要采用式(13)计算无人机集群的虚拟中心.

在式(13)的基础上,通过式(14)计算无人机集群的聚集指标.式(14)中,da为聚集指标.
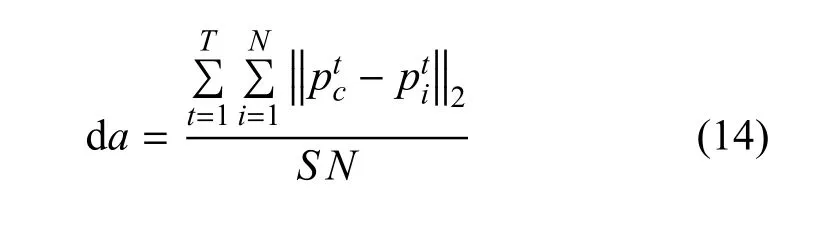
3 仿真实验及分析
3.1 仿真实验设计
仿真实验中涉及的模型,场景和算法类型如表1所示.
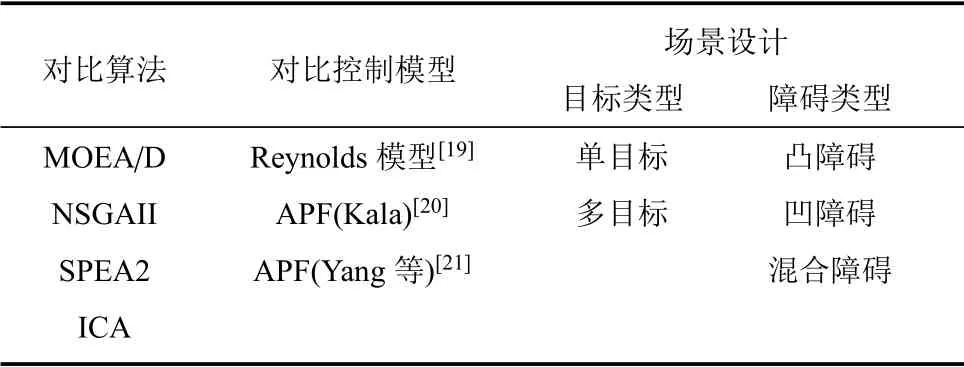
表1 仿真实验设计Table 1 Simulation experiment design
其中,仿真场景的具体设置如下:
1)任务区域设定为边长为500 的正方形区域.
2)无人机最大速度vmax=5/step.
3)自组织无人机集群规模被设定为20.
4)无人机间的通讯延迟被设定为1 step.
5)无人机传感器存在误差,误差范围为(0,1).
6)无人机传感器的探测范围取值为(45,5)中的一个随机数.
7)每个仿真场景的仿真时长上限被设定为200 step.
8)在全部场景中,无人机集群的任务均包括从开始区域出发飞向目标区域.在飞行过程中,无人机个体必须避免与任务场地内存在的障碍和任务区域边界或其他无人机个体发生碰撞.另外,在多目标任务中,无人机集群还需要按顺序到达任务区域内的其他目标点.
全部被测算法中,种群规模被统一设定为30,算法最大迭代次数被设定为200,变异系数被设定为30%.全部被测算法所使用的交叉算子和变异算子均与NSGAIII 算法相同.所有算法和仿真实验均运行在一台使用Intel R○CoreTMi7-6700HQ CPU(4核,2.6 GHz),32 GB 内存的电脑上.
3.2 优化算法表现分析
仿真实验对比了多种不同的多目标优化算法在RSCMTP 模型上的优化性能表现,主要采用不同算法的均值/最优表现分析以及基于超体积(hyper volume,HV)的多目标优化能力分析.给出优化算法表现分析所采用的测试场景如图7所示.
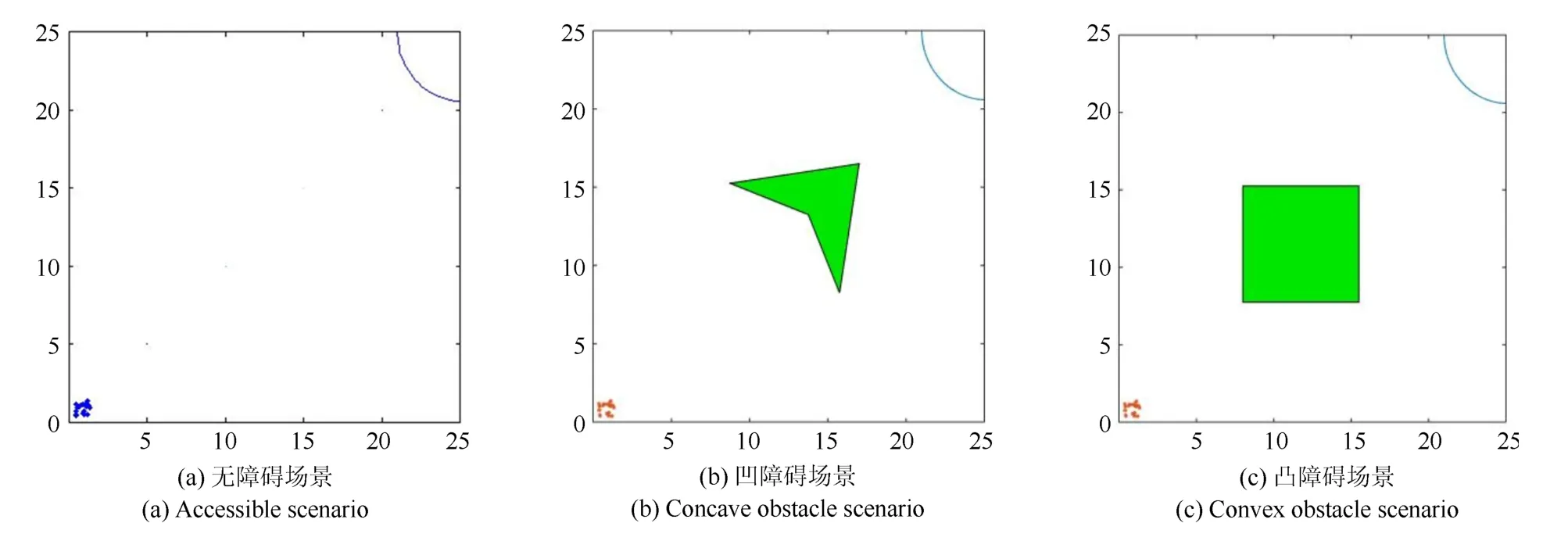
图7 算法效能测试场景Fig.7 Algorithm performance comparison scenarios
算法具体表现如表2、表3所示.
表2 中,“DR”代表死亡率,“TT”代表任务完成时间,“AI”代表聚集指标.从表2 可知,测试的全部3个场景中,NSGAIII 算法均能找到具有最好死亡率、聚集指标和任务完成时间的参数组合.
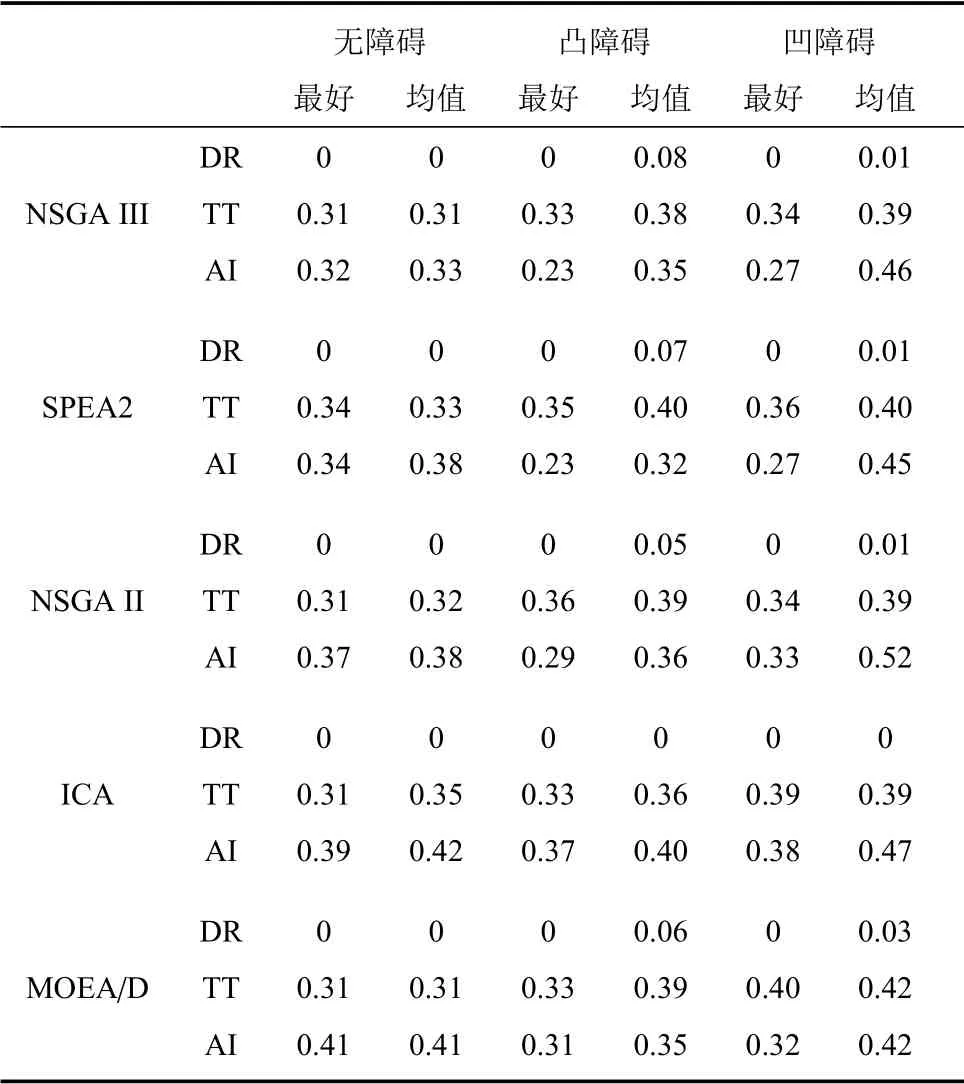
表2 最优/均值表现分析Table 2 Best/average performance analysis
在最优/均值分析的基础上,采用超体积分析方法测试不同算法的多目标优化能力.由于本问题的实际最优帕累托前沿未知,因此,使用一种基于蒙特- 卡洛方法的超体积分析方法.该程序可从网址https://ww2.mathworks.cn/matlabcentral/file xchange/30785-hypervolume-computation?s_tid=srchtitle_hypervolume4 获取.超体积分析的参考点下界设定为全部算法在3 个场景内取得的优化目标的最优值,参考点上界统一设置为{1,1,1}.每次仿真产生的采样点数量均为500 000,采样点分布均采用完全随机分布.为消除采样方法导致的随机误差,每个测试场景均执行20 次,并分别记录各个算法的平均超体积分析表现如表3所示.
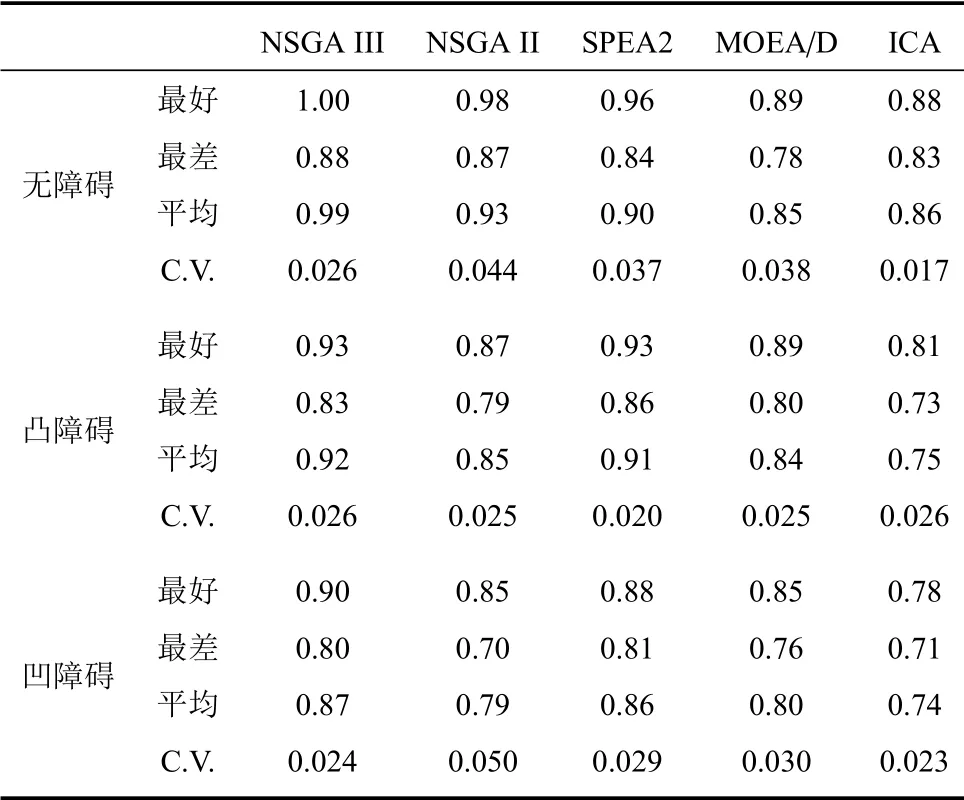
表3 算法超体积分析Table 3 Hypervolume analysis
由表3 可知,在测试的全部算法中,NSGAIII 在全部3 个测试场景中均能够获得平均和最差情况下的最好超体积分析表现.这表明从平均情况和最坏情况来看,NSGAIII 算法求得的帕累托前沿均能够覆盖最大范围的目标值空间.另外,表3 还展示了测试的全部算法的变异系数.从变异系数指标可得出结论,NSGAIII 算法在全部3 个测试场景中的超体积评价表现均具有较好的稳定性.
综合表2 及表3 的测试结果可得,NSGAIII 算法在测试的全部多目标优化算法中具有最好的优化效能表现.
3.3 控制模型表现分析
为测试参数调优后的RSCMTP 模型效能,设计了两类不同测试场景:1)多障碍场景;2)混合障碍场景.为决定本测试最终采用的RSCMTP 模型控制参数,对NSGAIII 算法在第3.1 节的3 个测试场景中求得的参数组合的评价值进行了线性加权聚合,该方法可由式(15)表示.
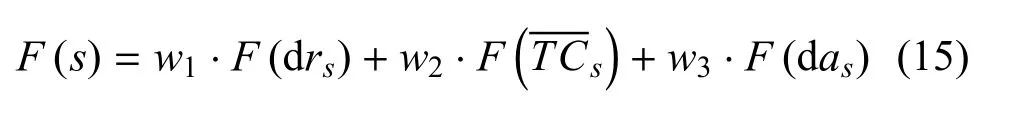
其中:
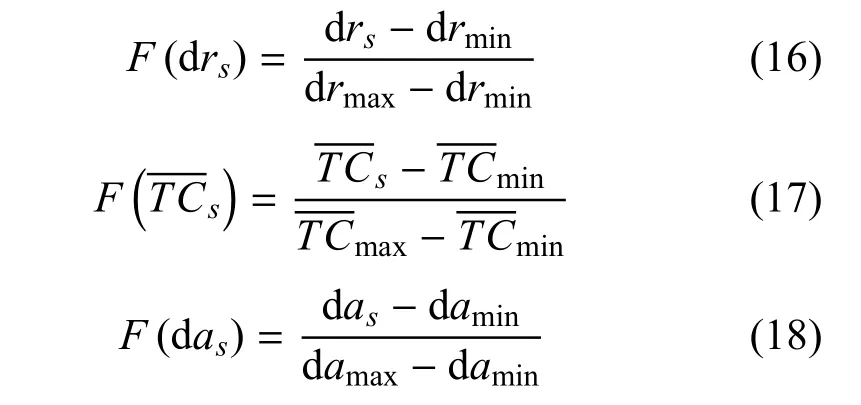
其中,分别为当前解的死亡率、任务完成时间、聚集指标.分别为死亡率、任务完成时间、聚集指标在该场景下的最小值.分别为死亡率、任务完成时间、聚集指标在该场景下的最大值.w1,w2,w3为代表各参数指标重要度的系数,在当前实验中,设w1=w2=w3=1/3,即认为3 个指标的重要度相等.
测试共包含4 种不同的控制模型,各模型表现如图8、图9所示.
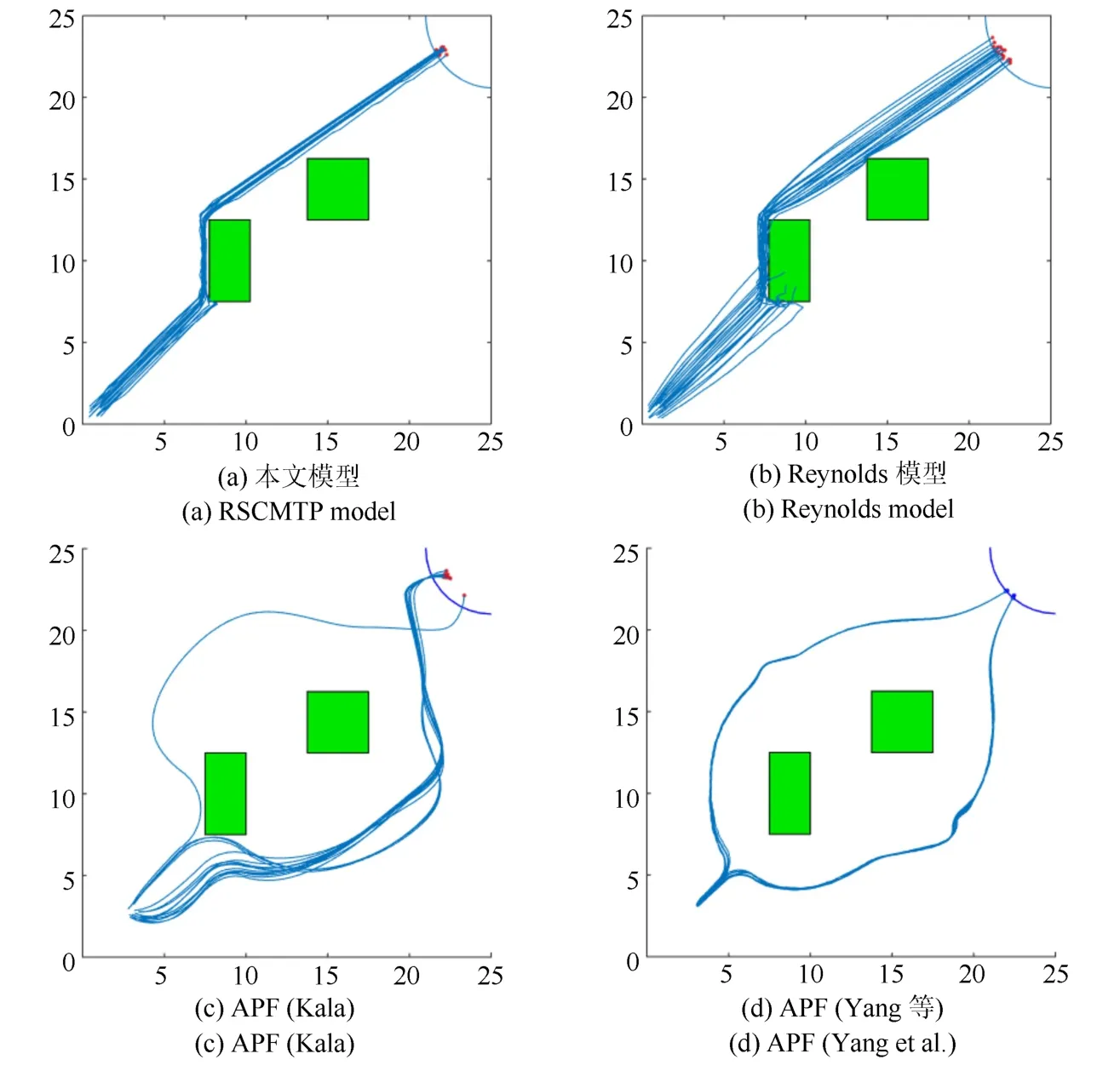
图8 多障碍场景Fig.8 Multi obstacles scenario
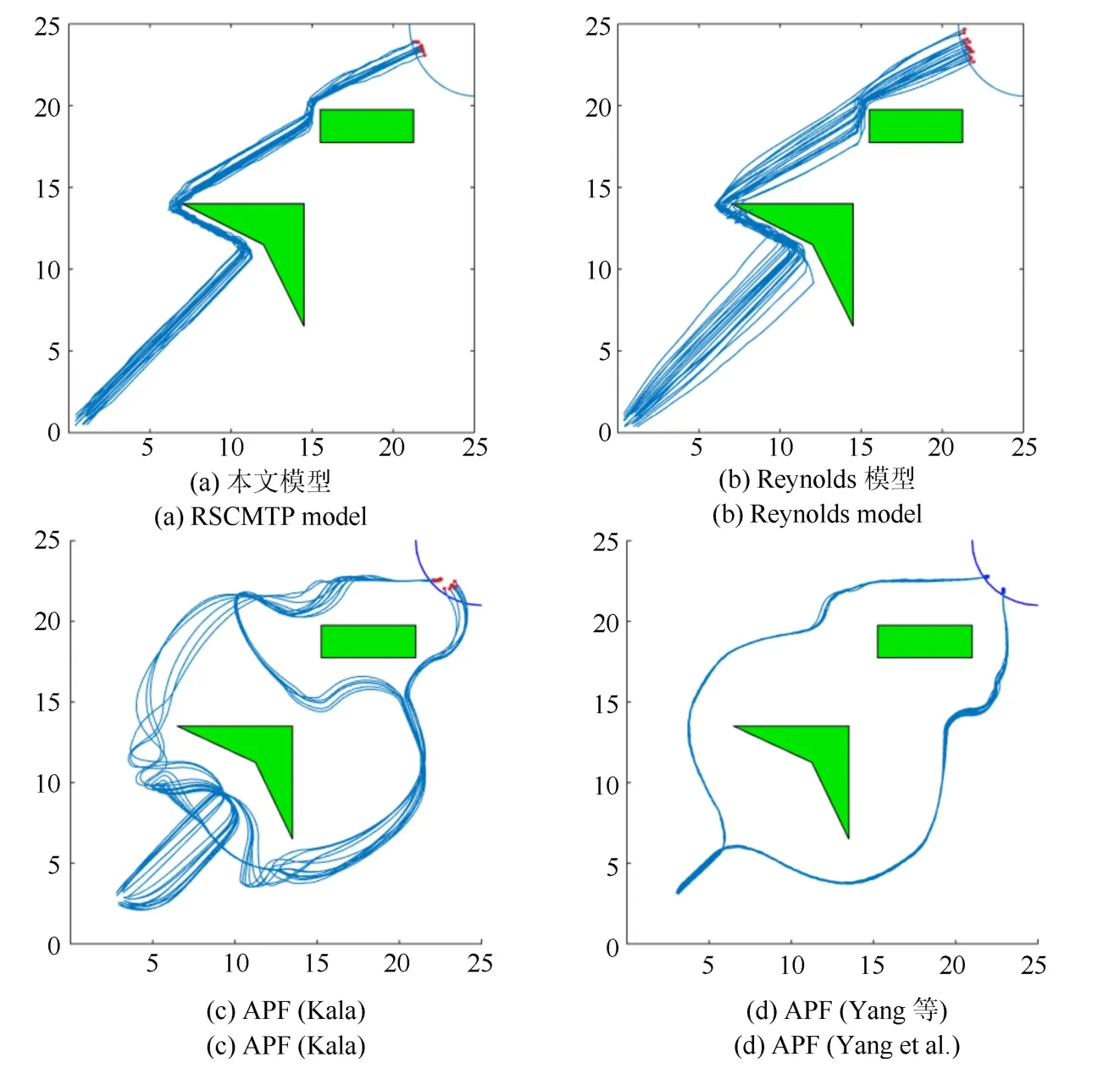
图9 混合障碍场景Fig.9 Mixed obstacles scenario
各项评价指标的具体评估结果如表4所示.
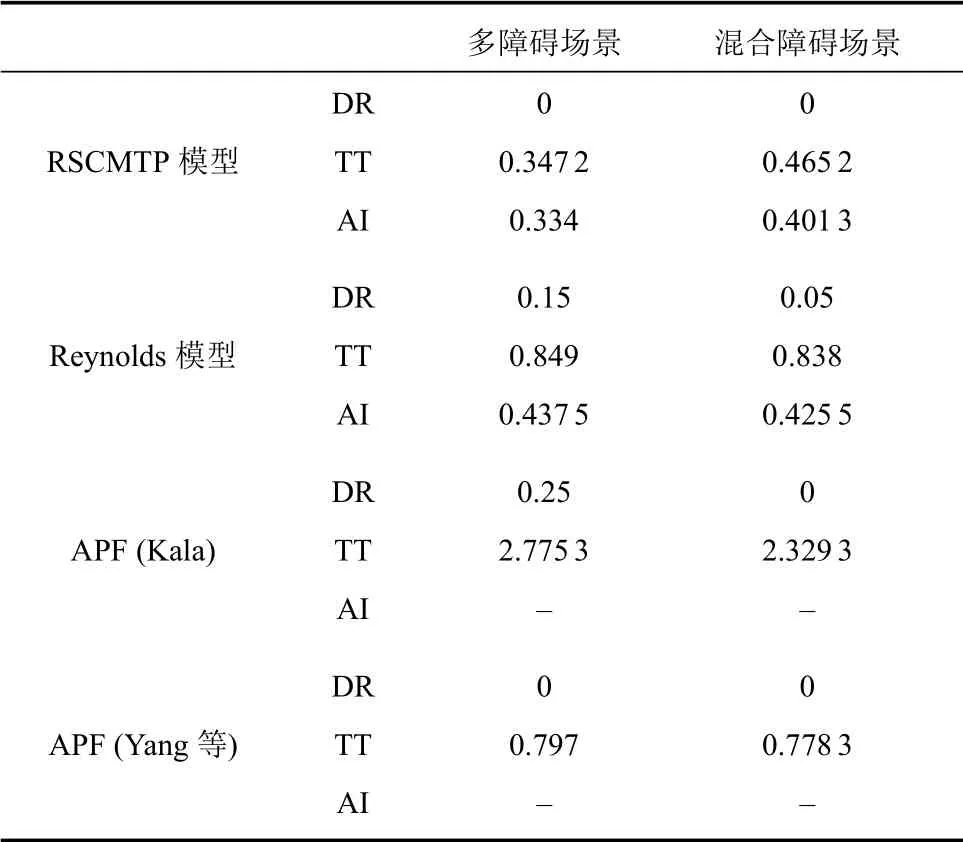
表4 控制模型表现分析Table 4 Control model performance analysis
如表4所示,参数调优后的RSCMTP 模型在两个复杂场景下均具有死亡率、聚集性和任务完成速度上的较大优势.需要指出,由于APF 模型在处理复杂障碍时倾向于分裂为多个小规模群体,因此,表4 中不再给出APF 模型的聚集性指标.显而易见的,RSCMTP 模型和Reynolds 模型对比APF 模型在聚集性上具有较大优势.
3.4 多目标场景分析
多目标任务场景中,自组织无人机集群需要从开始区域出发,途径任务区域内的多个中间目标点,最终到达目标区域.在两个测试场景中,串行任务场景代表无人机集群中的全部无人机需要按顺序依次通过多个目标区域;并行任务场景代表无人机集群需要自主分裂为多个集群,同时通过多个目标点,并最终集体到达目标区域.需要额外指出的是,由于APF 和APF 两个模型无法处理多目标问题,因此,仅给出Reynolds 模型和RSCMTP 模型在以下两类场景内的实验结果.
3.4.1 串行场景分析
串行任务场景中无人机集群控制模型的对比结果如图10 至图12所示.
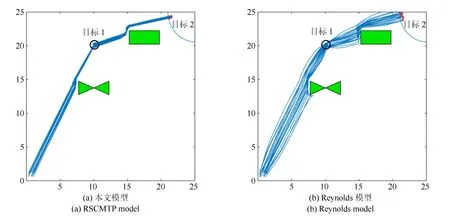
图10 串行任务场景1Fig.10 Multi-mission scenario 1

图12 串行任务场景3Fig.12 Multi-mission scenario 3
从路径规划结果可以看出,对比Reynolds 模型,RSCMTP 模型能够在任务执行的过程中维持更密集的队形,同时其避障性能更好,且规划后总飞行时间消耗也更低.其主要原因是经过参数调优后的RSCMTP 模型能够更加精确的控制不同环境下无人机个体受到环境施加的力的影响程度,从而提升模型的控制表现.由于串行任务场景能够分解为多个3.2 节中的存在障碍的导航场景,因此,该结果是可以预见的.
3.4.2 并行场景分析
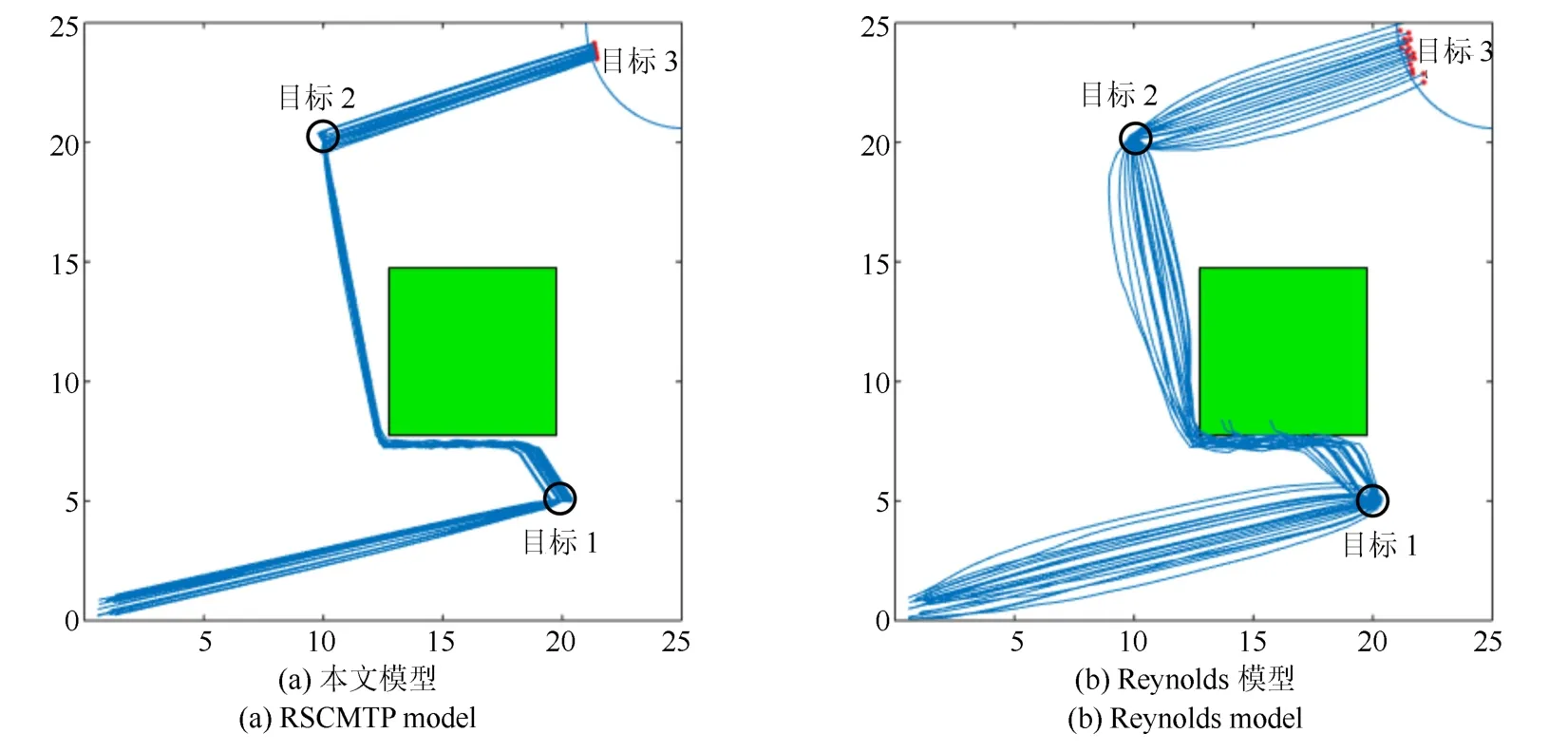
图11 串行任务场景2Fig.11 Multi-mission scenario 2
并行任务场景中,无人机集群中的个体需要分别前往不同的目标点,因此,无人机个体首先采用式(19)对目标进行评价:
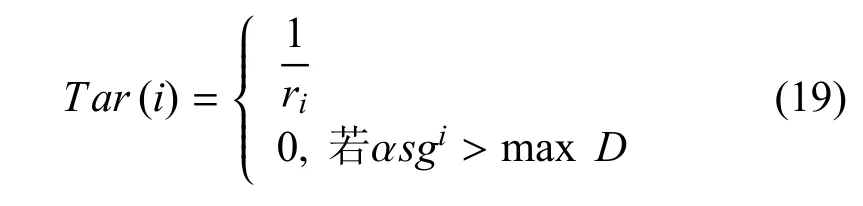
式(19)中,Tar(i)代表当前无人机对第i个并行目标的评分,ri为无人机距该目标的距离,asgi为该无人机观测到前往目标i方向的无人机数量,maxD为前往该方向的无人机的数量上限.maxD=numUAV/tartotal,其中,numUAV为该个体能够观测到的无人机总数,tartotal为并行目标总数.式(19)的基本含义为无人机会选择前往目前仍能够选择的距离其本身最近的目标点.并行场景测试结果如下:
图13 −图15 展示了存在并行任务的场景两种控制模型的路径规划表现.因在第3.2 节和第3.3.1节已经说明了RSCMTP 模型对比Reynolds 模型在任务完成速度和聚集性上具有较大优势,因此,本实验仅对比在多任务并行条件下RSCMTP 模型的效能表现.从图13−图15 可得出结论:并行任务环境下(特别是图15所示并行任务数量较多时),Reynolds模型已无法很好地满足队形保持和路径规划的要求,而RSCMTP 模型仍能够很好地维持队形,且无人机个体能够在多个并行任务间有效的作出自主选择.其主要原因是RSCMTP 模型能够根据任务需要平衡维持队形所需的力和任务目标对个体施加的引力之间的重要性关系,从而提高了控制模型表现.因此,可以得出结论:RSCMTP 模型对比经典Reynolds 模型,在处理并行任务时具有一定优势.
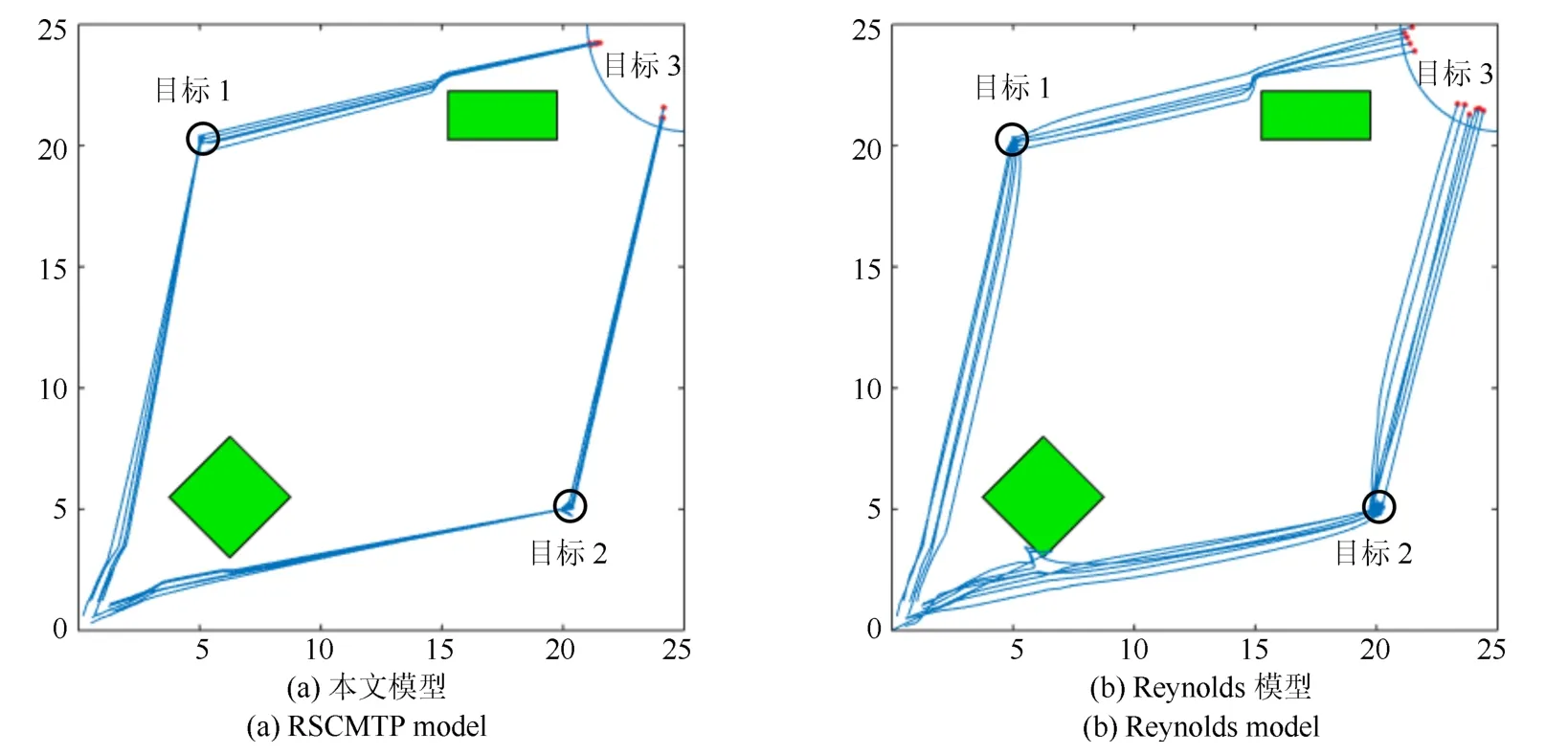
图13 并行任务场景1Fig.13 Parallel mission scenario 1
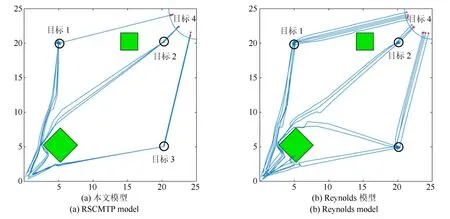
图15 并行任务场景3Fig.15 Parallel mission scenario 3
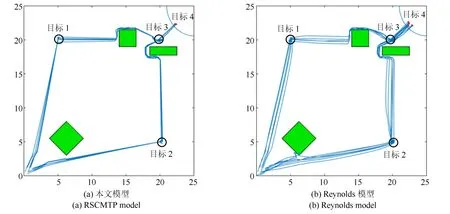
图14 并行任务场景2Fig.14 Parallel mission scenario 2
4 结论
提出了一种基于规则系统和多目标优化方法的自组织无人机集群航迹规划方法.该方法以经典的基于虚拟物理规则的速度更新模型为基础,在分析自组织无人机集群的典型任务场景的基础上,建立了针对导航、避障和编队队形维持任务的无人机集群控制规则系统.同时,设计相应的多目标优化方法求解了该系统中的控制参数.最后,设计多种不同的仿真对比实验,验证了该控制模型的有效性.
针对RSCMTP 模型的后续研究方向包括:1)仿真实验仅考虑了速度变化,未考虑无人机个体的加速度可能存在的上限.因此,未来的研究中,可以考虑设计针对无人机个体的加速度存在上限的控制模型.2)未考虑目标区域内的航迹规划问题.考虑到无人机集群的任务可能包括区域覆盖任务,未来可将目标区域内的航迹规划问题加入控制模型设计的考虑范围.3)用于求解RSCMTP 模型参数的NSGAIII算法所采用的算子均为通用算子,可以考虑针对该问题特性设计特定的操作算子,改善优化算法的计算表现.
