基于高弹性芯模缠绕复合壳体压力容器的结构分析

江 真，郑 庆，林天一，王林祥，鲁昊钺

(上海航天动力技术研究所， 上海 201100)

1 引言

复合材料压力容器具有轻质高强的结构特性，其材料组成及结构决定了复合材料压力容器特性具有系数高、负载寿命长且可设计性强的特点，在航空、航天、医疗、化工等各个领域都有广泛应用[1-4]。同时，随着碳纤维国产化进程的持续推进，国产碳纤维产量扩大化和价格低廉化，对CFRP(carbon fiber reinforced plastics)应用提供了可能性、适用性及经济性，也进一步推进了复合材料压力容器在国产军民航空航天器件中应用的步伐。因此，关于复合材料压力容器的性能和结构分析一直是研究的热点。目前，国内外学者对于复合材料压力容器的主要关注方向有：原材料性能的提升、先进成型方法及精细化仿真分析。其中有限元分析软件，如：ABAQUS、ANASY、Amnesia、Digimat、MATLAB 及计算方法的迭代更新，使得复合材料压力容器的仿真分析更加精准高效。

国内外有大量利用有限元分析方法对复合材料压力容器性能进行分析的报道：王荣国等[5-6]对压力容器结构以及树脂固化体系进行了系统分析，并利用有限元方法对超薄金属内衬复合材料压力容器结构进行了分析，其考虑了封头处复合材料的铺放角度和厚度变化，较为准确地反应了金属内衬复合壳体数值分析过程；佟丽莉等[7]应用微分几何理论，推导出了纤维缠绕复合壳体的非测地线缠绕轨迹、包角方程及绕丝头的运动方程，得到压力容器封头处损伤导致轴向变形，考虑了封头损伤对整体性能的影响。Lei Zu等[8-9]提出了一种用于确定基于非测地轨迹的复合材料压力容器的最佳绕组参数并借助于不同的理论和缠绕原理，利用MATLAB语言对复合材料压力容器的非测地线进行了仿真，验证了轨迹设计的有效性。RohamRafiee等[10]研究了不同失效准则下带/不带内衬的复合材料压力容器的首层失效(FPF)性能，并基于连续损伤的渐进失效模型预测压力容器的爆破压力，并考虑了纤维体积分数，缠绕角度及发挥强度等性质，建立了随机模型以估算复合材料压力容器的爆破压力。P.F.Liu等[11-12]总结了用于预测复合材料容器的失效特性和退化损伤机理的建法，和预测复合容器爆破压力和寿命的方法，解释了复合材料容器的失效特性和刚度退化机理。Q.G.Wu等[13-14]通过数值模拟分析了损伤演化对爆破压力和自紧压力测定的影响规律。周丹等[15]研究了不同铝合金内衬下，复合压力容器气瓶的应力和损伤的对比分析。

上述已经开展的工作，大多关注对薄壁金属内衬压力容器进行有限元分析，而对于工艺更为复杂且应用更具前景的带高弹性芯模装填介质一体缠绕分析鲜有报道。本文中主要在现有推导张力的基础上，对高弹性芯模的缠绕张力制度进行理论分析和试验探究，利用有限元分析方法对带高弹性芯模一体缠绕成型壳体结构进行应力应变模拟分析，并与试验数据进行对比验证，以期为该项工作的进展提供理论及试验参考。

2 理论公式

理论公式主要为满足设计压强的高弹性芯模缠绕成型提供理论基础，主要分为等张力缠绕的张力制度和满足设计压强下的缠绕线型设计。

2.1 等张力缠绕模型

缠绕张力制度对复合材料压力容器性能的影响主要体现在以下几个方面[16]：1)影响壳体力学性能；2)影响壳体含胶量；3)影响缠绕壳体密度和孔隙率。因此，缠绕张力制度对缠绕壳体性能至关重要，需采用等张力缠绕制度。根据刘成旭等[17]对缠绕张力和剩余张力的研究，等张力缠绕可设均匀缠绕后的剩余张力T(x)可表示为：

(1)

式中：t为初始缠绕张力值；H为与模型尺寸相关的参数；m为缠绕后和缠绕前模型外半径的比值；x为不同缠绕厚度的模型的外半径与缠绕前模型外半径的比值。

采用初始张力和张力递减制度设置，利用MATLAB进行数值拟合，加入缠绕工艺的经验参数，最终可确定缠绕过程中的张力设置。

2.2 缠绕线型设计模型

复合材料压力容器设计原理一般有：网格理论、经典层合板理论、一阶剪切理论、高阶剪切理论、叠层理论和弹性理论等。本文主要结合网格理论以及经验公式总结出适合高弹性芯模缠绕公式。

根据设计压强值对缠绕层螺旋方向缠绕角进行计算:

(2)

式中：d1为前端极孔；d2为后端极孔；Dout为筒体段外径。

螺旋向纤维层厚度hα及环向纤维缠绕厚度hθ计算：

(3)

(4)

式中：Pmax为内压；Ksafe为安全系数；ks为应力平衡常数；σfb为纤维发挥强度。复合壳体筒身段计算：

(5)

式中：Vf为纤维体积含量。

壳体螺旋向与环向缠绕层数n的计算：

(6)

式中：h为螺旋向或环向厚度；b为纱片宽度；m为纤维团数。

将设计要求代入公式进行计算，得出缠绕参数，进行缠绕。

铺层方案：[±90/±24/90/±24/±90]，共9层，理论壁厚1.62 mm。

缠绕张力：为58～50 N逐层递减。

固化制度：70 ℃固化8 h，逐渐降温至50 ℃固化2 h。

3 试验及仿真模型

复合材料压力容器具体尺寸如图1所示，复合壳体外径设计值约为Ф160 mm，直筒段纤维层设计缠绕厚度为1.62 mm，复合壳体加前后堵头总长约为339 mm，整个复合壳体由前后封头，前后堵头以及碳纤维缠绕壳体组成，其中复合壳体内部为高弹性芯模复合层。前后封头为等开口孔径，直筒段的缠绕方式包括螺旋缠绕和环向缠绕，封头段缠绕方式仅为螺旋缠绕。设计缠绕模型如图1所示。

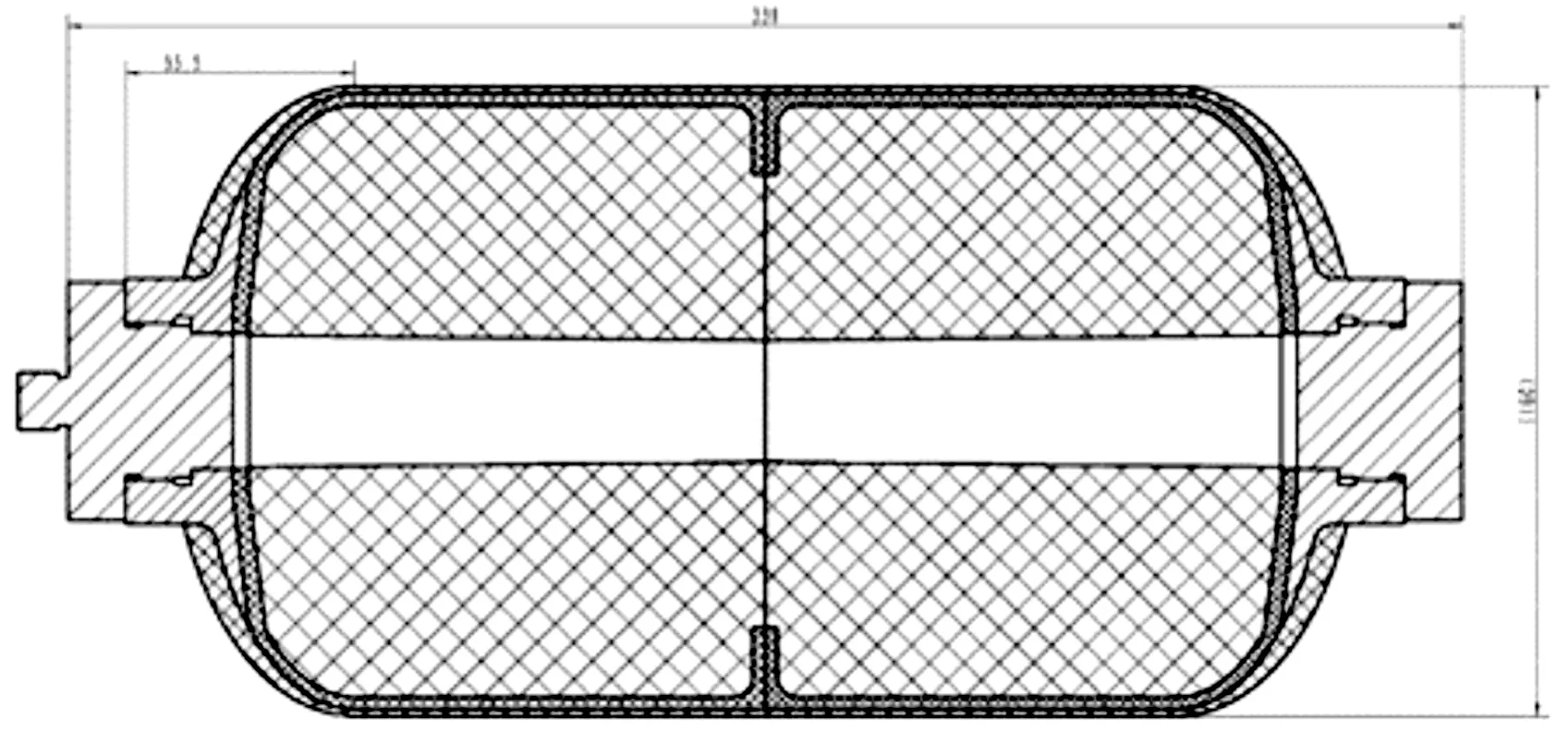
图1 设计缠绕模型示意图Fig.1 Diagram of winding model design

4 计算结果及分析

对带高弹性芯模缠绕复合壳体进行液压仿真，材料参数如表1～表3所示，仿真模型如图2所示。

图2 燃烧室壳体应变仿真模型示意图Fig.2 Strain simulation model of the combustion chamber shell

表1 计算所用金属材料物性参数

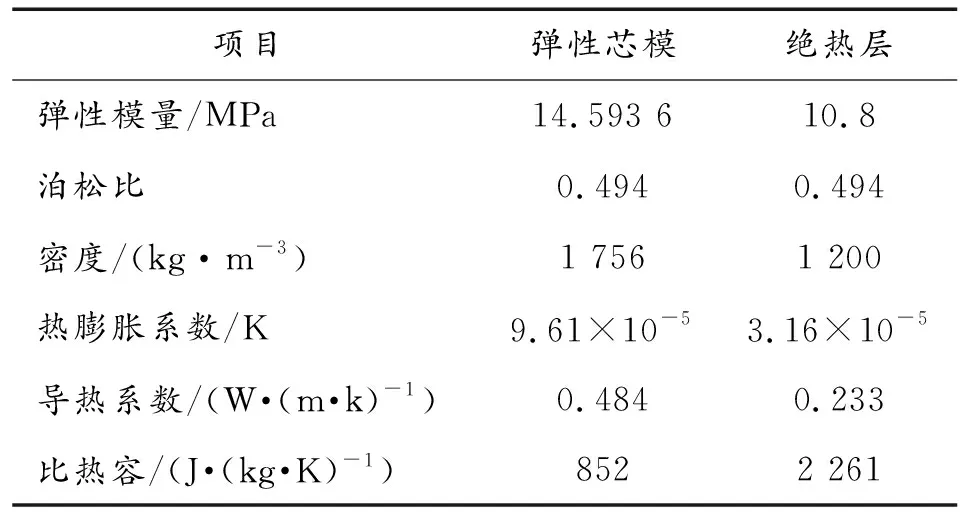
表2 高弹性芯模材料物性参数

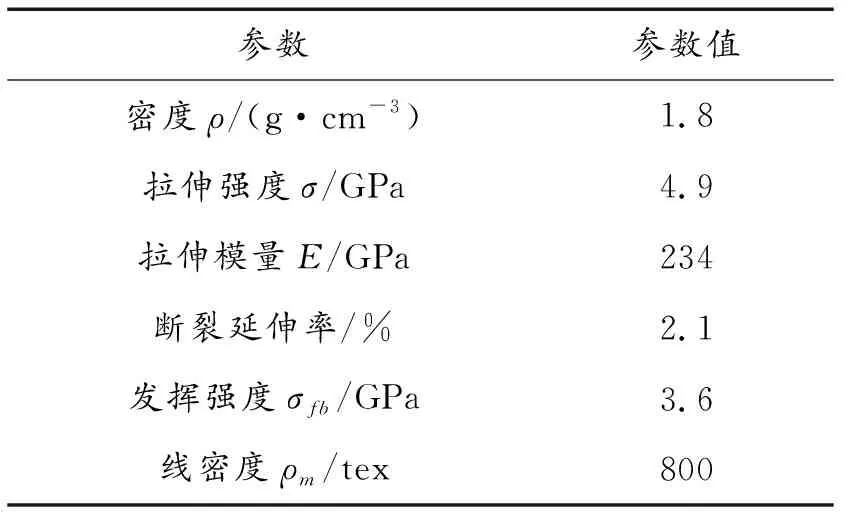
表3 T700SC-12K碳纤维物性参数

弹性芯模松弛模量为：

E(t)=14.593 6(0.035+0.354 4e-t/0.001 826 9+

0.230 2e-t/0.018 269+0.141 1e-t/0.182 69+

0.029 3e-t/1.826 9+0.057 2e-t/18.268 6+

0.039 6e-t/182.686 1+0.024 1e-t/1 862.860 7+

0.057 2e-t/18 268.607 1)

(7)

时温移动因子用WLF方程表示：

lgαT=-10.603(T-20)/(222.815+T-20)

(8)

参考温度为20 ℃。

网格划分：根据不同部件材料特性对壳体结构进行网格划分，多采用六面体结构化网格，并对关键部位进行局部加密网格设置以确保仿真结果的可靠性，网格质量检查结果良好。

载荷条件分别为：仿真1内压为10 MPa，仿真2内压为5 MPa。边界条件为：端面固定约束，1/4截面环向对称。

4.1 带芯模复合壳体结构仿真

对应工况下的仿真云图如图3～图6。从云图可以得到，10 MPa和5 MPa的云图各项分布规律一致，从壳体来看，直筒段的应力及变形量较封头处更大，最大应力值为515.5 MPa，且在两芯柱之间出现应力集中情况，分析原因主要是因为芯柱之间未进行完好粘接，导致液压直接作用在芯柱端面，对中间处壳体产生拉力导致。封头处，应力和应变均出现变化不均匀现象，主要是纤维缠绕方向导致的承载力不均所致，该仿真工况与试验真实情况保持一致。直筒段的环向应变值接近直筒段的主应变值，而封头段的环向应变值明显小于封头段的主应变值。芯柱的应变云图可以侧面验证壳体所受应力分布，从图6可以看到，芯柱内型面承受较大应力，且中间粘接面较附近区域出现局部应力集中，应力整体分布由芯柱内部向外表面逐渐递减。

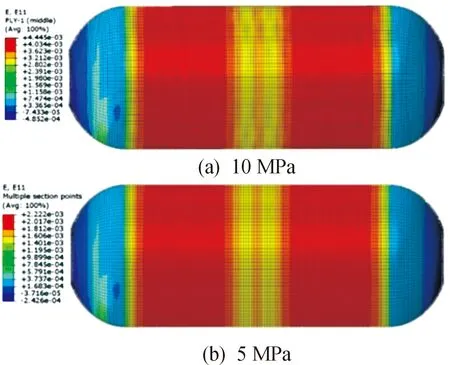
图3 壳体环向分布云图Fig.3 Cloud diagram of the shell ring distribution

1) 壳体环向应变仿真结果

2) 壳体主应变仿真结果

图4 壳体主应变分布云图Fig.4 Cloud diagram of shell principal strain distribution

3) 壳体主应力仿真结果

图5 壳体主应力分布云图Fig.5 Contour diagram of shell principal stress distribution

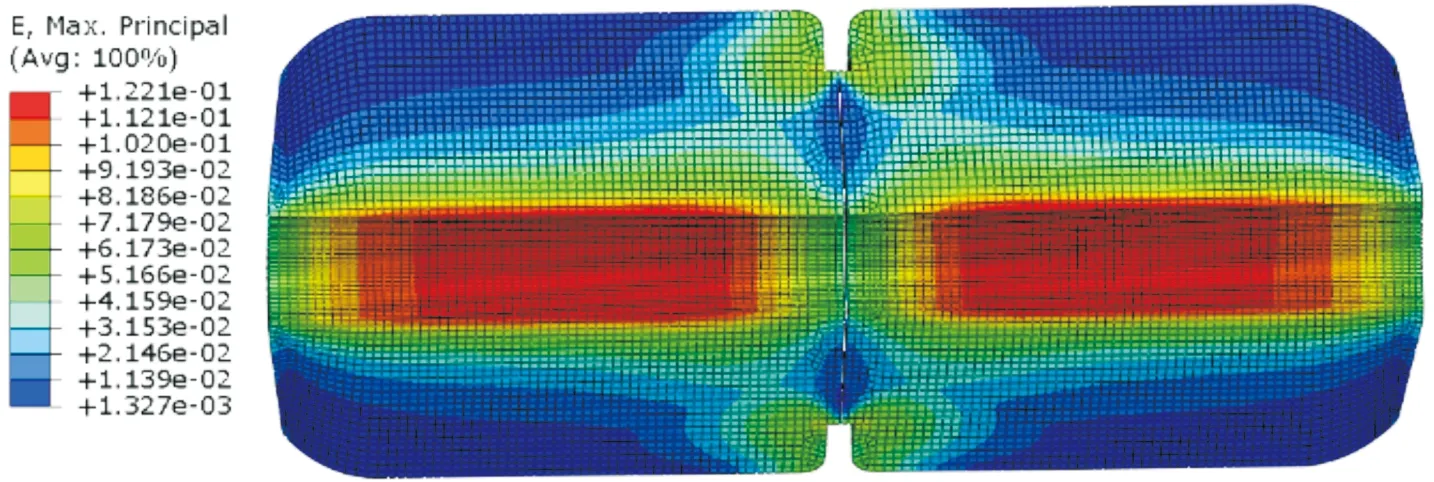
图6 芯柱主应变云图Fig.6 Principal strain cloud diagram of core column

4) 高弹芯柱仿真结果

4.2 仅复合壳体结构仿真

将复合壳体内部高弹性芯柱去掉，在相同工况下进行壳体力学性能的模拟，分别在10 MPa和5 MPa内压下进行有限元分析，并与复合壳体仿真结果进行对比。仿真云图如图7～图9。从云图中可以看出，纯壳体筒体段应变、应力分布均匀一致，没有应力集中，且较封头段的值较大，最大应力值为764.3 MPa，比带高弹性芯柱复合壳体应力最大值大。直筒段的环向应变值与直筒段的主应变值接近，封头段环向应变小于封头段主应变，此规律与带芯柱壳体一致。

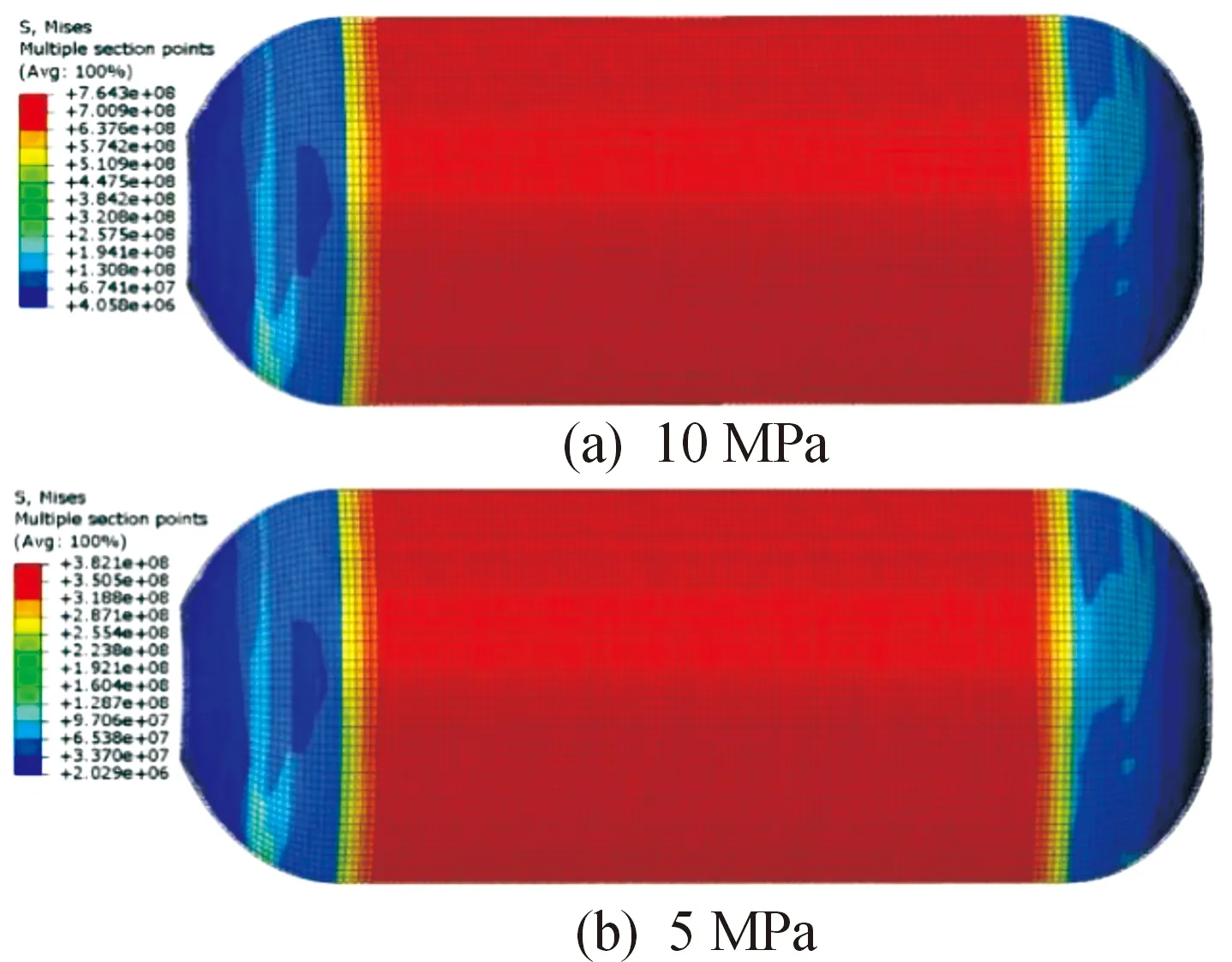
图7 纯壳体主应力分布云图Fig.7 Cloud diagram of principal stress distribution of pure shell

图8 纯壳体主应变分布云图Fig.8 Cloud diagram of principal strain distribution of pure shell

图9 纯壳体环向应变分布云图Fig.9 Cloud diagram of hoop strain distribution of pure shell

4.3 仿真与试验结果对比

按上述公式以及经验得到的等近张力缠绕制度进行缠绕，得到复合壳体进行液压实验，与仿真结果进行对比分析，共计采取12处具有代表性的特征点进行应变测试，1～7点沿轴向分布，测试点1’～4’沿径向分布；采用三向应变栅，应变栅0°方向对应壳体轴向，90°方向对应壳体径向，进行应变采集，如图10。测试现场布置如图11所示。在液压为5 MPa下保压30 s，在10 MPa下保压30 s，无渗漏。液压测试误差为±0.3 MPa。

图10 复合壳体缠绕后示意图Fig.10 Schematic diagram of composite shell after winding

图11 复合壳体应变测试现场布置示意图Fig.11 Strain test of composite shell

测试各采集点的应变如图12所示，测试各点的应变随时间变化而变化，试验时内压由5 MPa升至10 MPa，卸压后，应变曲线出现明显的下降平台。整体应变曲线与壳体液压变化规律一致。

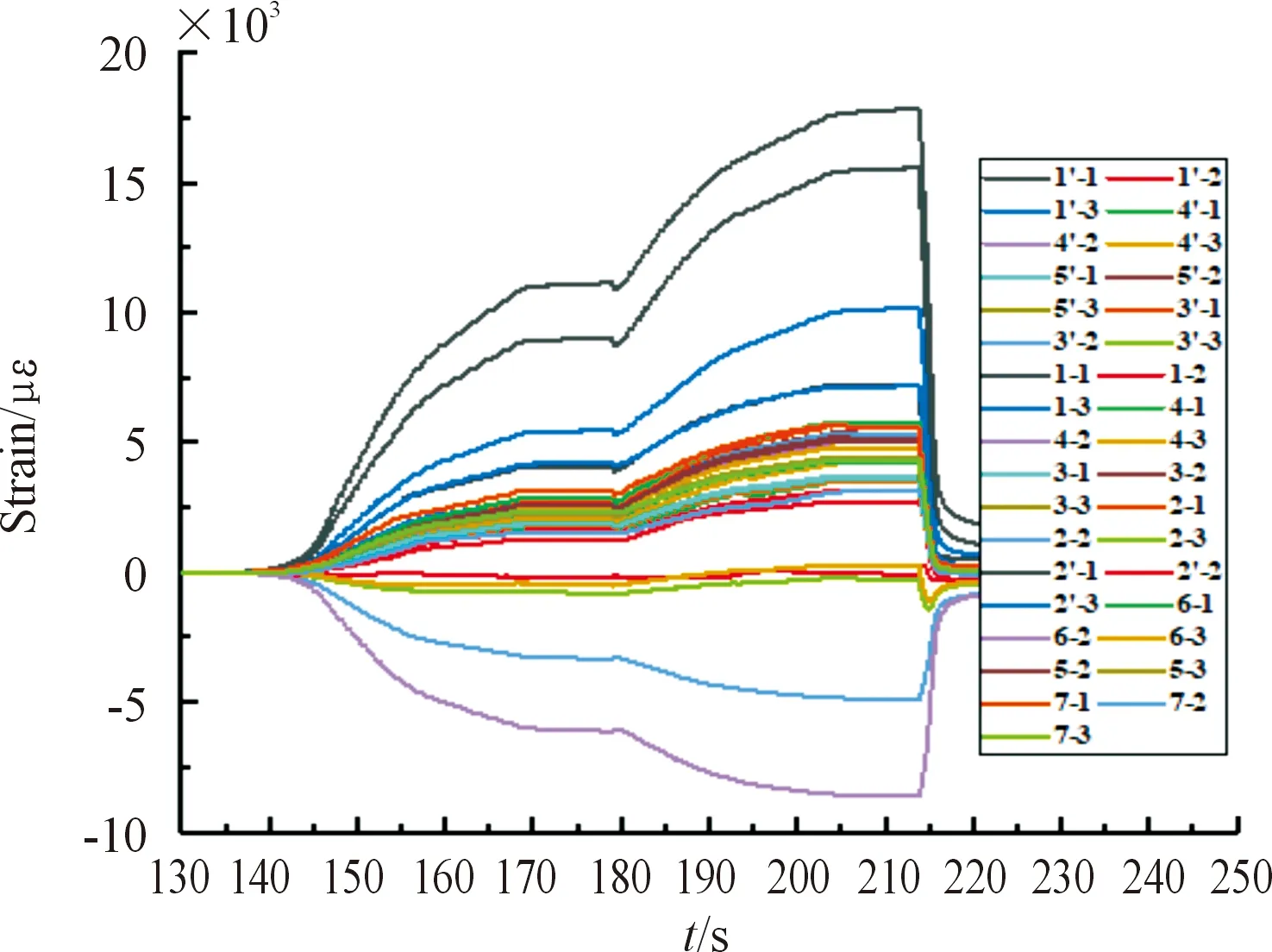
图12 应变曲线Fig.12 Strain curve

试验结果与仿真结果的对比如表5所示，从有限元分析值与试验值的对比，直筒段有限元分析值与试验值较为接近，误差在5%～20%，且数值分布均匀稳定。封头处的仿真误差在30%左右，封头处的测试值出现较大负值，对照环向应变仿真云图中出现的负值进行分析，主要是因为芯柱封头按照椭球封头成型，对于一般椭球比为2的椭球封头而言，成型在中间部位缠绕封头处，会出现较大凸起，加上端部纤维逐渐堆积，凸出较封头初始端更加明显，因此，应变在该凸起处为拉应力，而在初始端则会出现局部压应力现象。封头处建模采用层合板铺层方法，与实际缠绕过程中纤维角度连续变化稍有出入，后续将通过编程进一步精细仿真模型，进行计算。

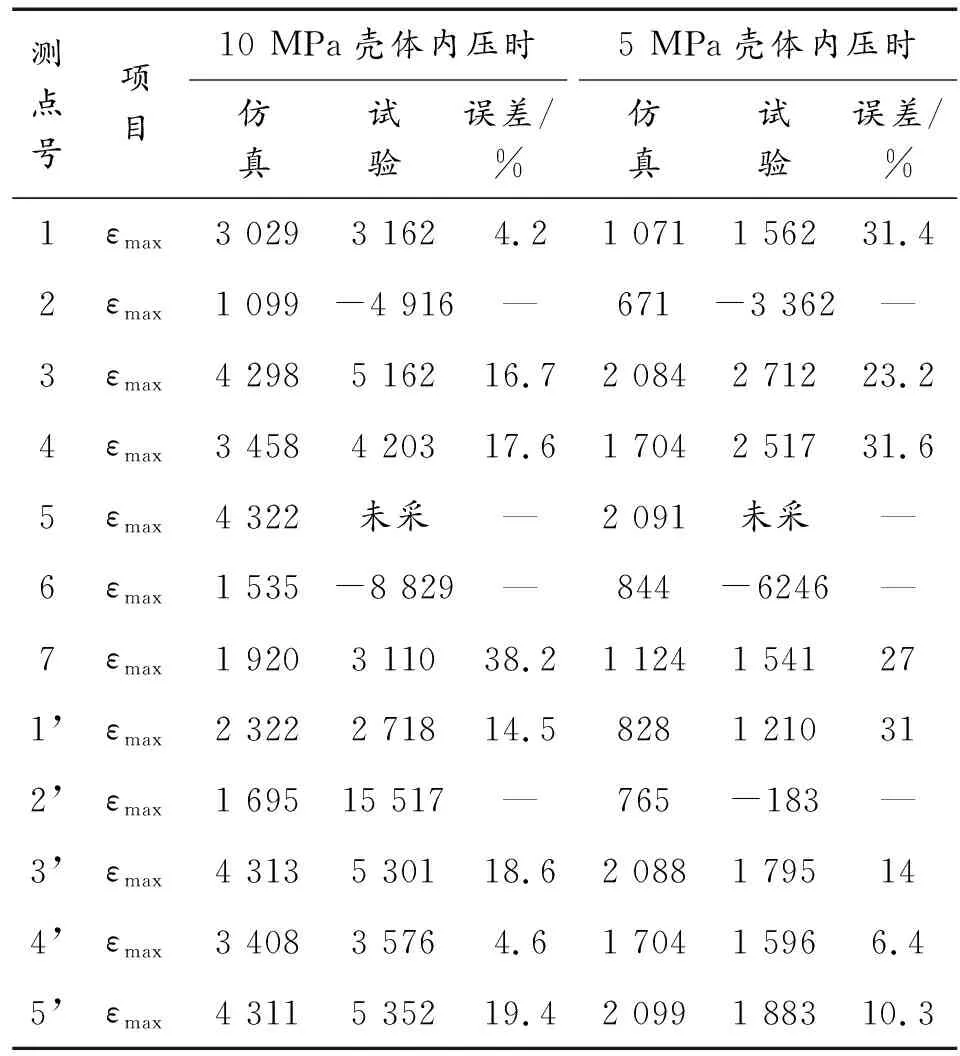
表5 试验与仿真应变值

有限元分析值和实验值均显示，在直筒段的应变值较大。筒体中间处，芯柱粘接面对应的壳体表面出现应力集中，这是因为芯柱粘接面界面强度较弱，内腔压力作用于芯柱粘接面上，相当于大部分作用在外层的纤维缠绕壳体上，形成整个壳体的薄弱点。

由表5中可知，封头处的1、1’、2、2’、6、7点处数据差别较大，且与筒体段的最大差别在于封头处环向应变值较轴向应变值小，为将数据进一步对比，将封头单独点处应变进行分析，如图13所示。

从图13中可以明显看到，2、2’和6号点处封头环向应变呈负值，1、1’和7号点处封头环向应变值为正值，此测试数值由于封头椭球比造成。封头处环向应变值最小，与筒体段规律相异，该结果与仿真得到的规律一致。

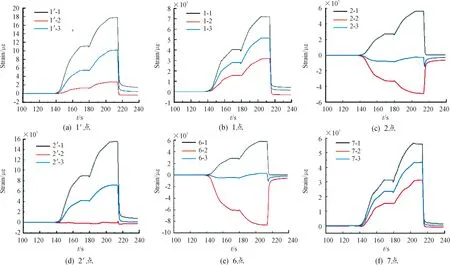
图13 封头段各点应变时间曲线Fig.13 Strain time diagram of each point in the head section

纯复合壳体的仿真与带高弹芯模复合壳体仿真结果对比表明，有芯模情况下，芯柱分担一部分应力和应变，导致壳体表面的应力应变值大大降低，在封头部分，仿真结果值与试验值误差稍大，分析误差主要体现在封头处缠绕纤维堆积，使得该处纤维层厚度及纤维缠绕角度急剧变化造成，仿真结果变化趋势与试验结果一致。对于筒体段的应力集中，后期将进行结构设计优化，增强芯柱粘接面的界面强度，以期提高复合壳体的整体刚度和力学性能。

5 结论

1) 复合壳体筒体段仿真结果与试验结果趋势一致，且仿真结果精度较高，该仿真模型及方法可靠。

2) 高弹性芯模可大大降低复合材料层应力，对提高复合壳体爆破压强具有重要作用。

3) 封头段应力从端部到直筒段呈现拉伸到压缩再到拉伸的趋势。