基于hp-RPM的滑翔弹道优化及制导仿真
2021-10-15陆秋秋易文俊
陆秋秋,易文俊
(南京理工大学 瞬态物理重点实验室, 南京 210094)
1 引言
滑翔制导炮弹是一种由导航制导系统指挥飞向目标的无人驾驶飞行装置。弹道优化是指在特定约束条件下,使导弹达到增加射程、保证精度等战术指标的控制机制。
为了保证打击威力,通常要求导弹在击中目标时具有较大的落角。该类型的方案弹道的设计可以看作是一个带有状态约束、控制约束和终端约束的最优控制问题(optimal control problems,OCP)。在解决轨迹优化问题时,通常采用间接法和直接法这两种数值方法。间接法将OCP转化为Hamilton多点边值问题的求解,从而获得最优控制律,在早期的轨迹优化问题中得到广泛的应用[1-4]。但是间接法很难求解复杂OCP中的两点边值问题,在实际的工程应用中受到限制,所以结构简单、收敛快速的直接法成为当前轨迹优化问题的研究热点。伪谱法(pseudospectral method,PM)是一种常用的求解最优控制问题的直接数值方法,它利用一组正交基在离散点对状态变量和控制变量进行逼近,把连续时间内的最优控制问题转化成为一个非线性规划问题(nonlinear programming problems,NLP)来求解,具有高精度、高效率和全局性的特点,适用于现代数字计算机运算,在轨迹优化领域有着广泛应用[5-7]。在伪谱法中采用网格自适应技术,根据某种误差准则自动调整网格细化方式和插值多项式次数,可用较少的计算代价获得较高精度的解,更适合状态变量和控制变量曲率变化明显的优化问题[8-9]。
由于计算误差、模型误差和外部干扰等因素的影响,导弹在实际飞行过程中的弹道有可能偏离预先计算的方案弹道。在实际飞行中,如何使导弹满足既定目标的问题称为导弹的再入制导问题,其核心是根据导弹的当前状态在线生成一条可行的再入飞行参考轨迹,然后设计一种跟踪此参考轨迹的强鲁棒性的控制方法,以克服模型误差、计算误差和飞行过程中的外部干扰[10-11]。由于复杂作战指标的要求,计算能力的提高,以及数值优化算法的改进,使得再入制导算法朝着实时在线、自适应的方向发展。
本文中对某型号滑翔制导炮弹在滑翔段的轨迹优化和再入制导问题进行了研究。采用舵偏角变化率作为控制变量,以最短滑翔时间为性能指标,利用hp-RPM方法设计了按一定落角打击地面静止目标的方案弹道。根据实际飞行过程中由于测量不准和阵风干扰造成的误差,提出了一种基于hp-RPM方法的在线制导方案,实现了滑翔段最优控制律的在线生成。
2 滑翔弹道优化模型
为更好地描述滑翔段导弹的位置和姿态信息,同时为方便问题的研究,本文中仅考虑导弹在纵向平面内的运动,偏航平面内的运动可以用类似方法分析。在以上假设的基础上,建立导弹在滑翔段的质心运动方程组:
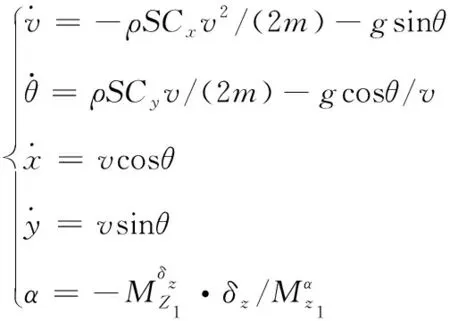
(1)
式中,(x,y)为导弹的位置坐标;v为导弹速度;θ为弹道倾角;S为参考面积;ρ为空气密度;α为攻角;δz为舵偏角;Cx和Cy分别为全弹阻力系数和全弹升力系数。
弹道优化本质上是在各种参数约束条件下,通过寻找最优控制方式u(t),使导弹从一个状态转移到另一个状态时的性能指标J最小(或最大)的非线性OCP,常用Bolza模型描述:
(2)
式中:x(t)∈Rn表示n维状态向量;u(t)∈Rr表示r维控制向量;f(·)∈Rn表示n维状态方程函数向量;J∈R是性能指标;Φ为终端性能指标;g为动态性能指标;φ为始端和终端约束函数;c为状态转移过程中参数约束。接下来,根据研究内容具体化Bolza模型中的各项参数和约束。
各种状态变量在导弹飞行过程中的约束称为状态约束,在弹道起点和终点处的约束称为端点约束。本文选取速度v、弹道倾角θ、水平距离x、飞行高度y和攻角α作为状态变量。具体而言,为了确保导弹对地面目标的毁伤效果,必须限制导弹在终点时刻的速度和弹道倾角:
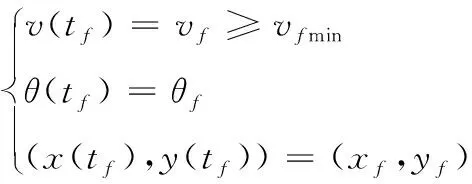
(3)
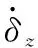
(4)
在滑翔过程中,除了状态参数和控制参数以外的其他自定义参数需要满足的约束都被称为路径约束。由于弹体强度有限,通常要求导弹的法向过载不超过限制值。此外,导弹的舵偏角也存在上限。路径约束见式(5)和式(6):
|ny|≤nymax
(5)
|δz|≤δzmax
(6)
本文探究能在最短滑翔时间内命中固定目标的最优舵偏控制方案,其性能指标采用Mayer型表示:
minJ=tf
(7)
3 基于hp-RPM法的带落角约束弹道优化
本文采用Radau伪谱法(RPM)将OCP问题转化为NLP问题求解[12],并用hp自适应方法自动调整子网格的数目及网格内多项式的阶数,既保证了计算精度,又提高了求解速度。
假定原OCP问题的定义域[t0,tf]被划分成K个网格子区间[tk-1,tk],k=1,2,…,K,设x(k)(t)和u(k)(t)分别代表第k个子区间中的状态变量和控制变量。因为Legendre方程的定义域是(-1,1),所以把变量t映射到τ∈[-1,1],转换公式为:
(8)
3.1 牛顿迭代法求LGR离散点
分别用Nk+2次和Nk+1次Lagrange多项式插值来近似状态变量和控制变量,即:
(9)
(10)
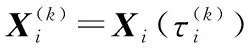
(11)
(12)
对式(9)求导以逼近原状态方程的导数,有:
(13)
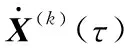
(14)
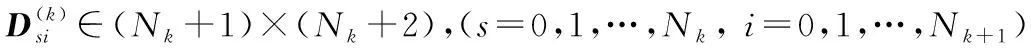
(15)
状态变量在区间[t0,tf]内的边界约束为:
(16)
状态变量在飞行过程中的路径不等式约束为:
(17)
3.2 hp网格自适应配置
本节给出一种hp网格自适应调整策略,该策略根据自定义的误差评估准则来判断网格是否需要细分或增加多项式阶数。当网格子区间的误差超出允许范围时,需要调整网格的数目、网格的长度或多项式阶次,以提高求解精度。
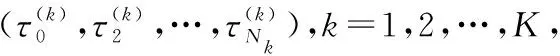
(18)
(19)
则动态约束方程和过程约束方程在上述采样点的近似误差估计为:
(20)
(21)
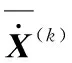
(22)
(23)
定义第k个网格内的误差最大值为:
(24)
各项目单位每月至少开展1次活动,一年开展不少于12次活动;活动类型不少于3种;每种类型活动不少于4次;每个小组活动不少于4节。
若第k个网格内精度不满足要求,需根据曲率决定是否细分该网格或增加其中的多项式阶数,定义第k个网格子区间内各点的曲率为[15]
(25)
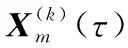
(26)
设置rmax>1为用户自定义的容忍相对曲率,若r(k)≥rmax,说明这一段网格内的曲率变化较大,需将该网格划分成更小的子区间,将第k个网格分成nk个更小的网格子区间的计算方法为:
(27)
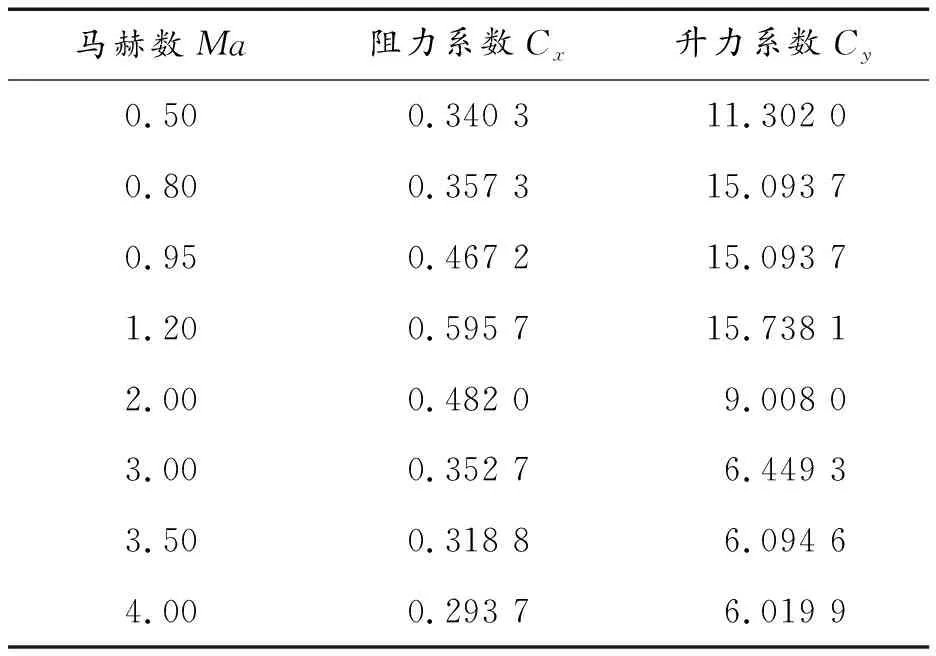
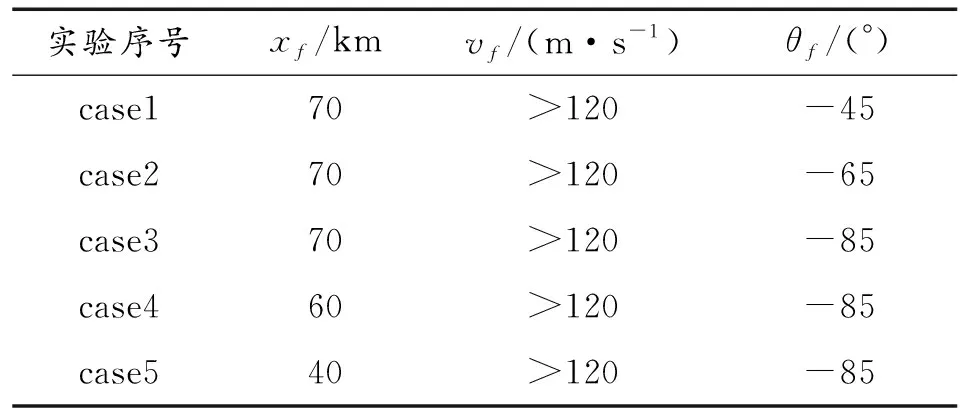
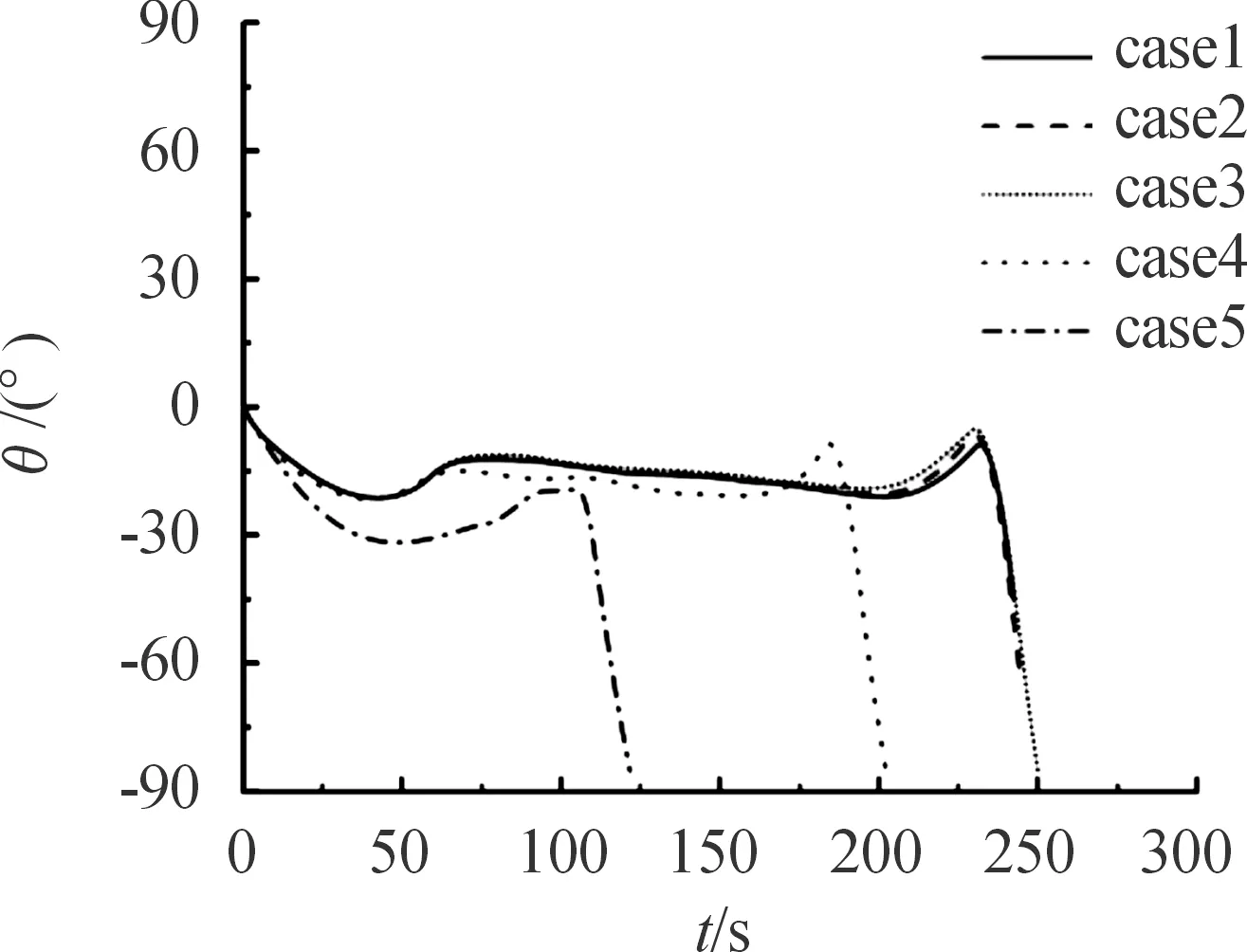
如果r(k) (28) 根据战术指标和发射条件,可以离线求解导弹的最优轨迹和控制量变化规律。导弹在实际飞行过程中直接依据离线控制律进行导引的方法称为开环制导。但是由于模型参数误差和外部干扰等不确定性因素的影响,导弹的实际轨迹和各项弹道参数往往会偏离基准弹道。本文提出的在线闭环制导策略中,测量系统获得当前制导周期初始时刻的实际弹道参数,并以此为初始值在线生成下一个制导周期的控制规律,当前制导周期的长度由hp-RPM算法的运行速度决定,反馈制导的具体步骤如下: 1) 假设t0为初始时刻,x0=x(t0)为初始状态变量,选定初始迭代网格数目和多项式次数后,利用hp-RPM方法离线计算出开环最优控制律u0。 3) 假设ti为测量系统第i次采样时刻,在时间[ti-1,ti](i=2,3,…)内,用控制律ui-1控制导弹的飞行,并记录ti时刻弹丸各项状态变量为xi=x(ti)。以xi作为新的初始状态,利用hp-RPM方法更新剩余弹道的控制律ui,假定优化程序的运行时间为Δti,则下一次测量系统采样时间即为ti+1=ti+max[Δti,1],令i=i+1。 4) 判断导弹是否击中地面某目标,若未击中,则返回步骤3);否则,退出循环。 以某型号滑翔制导炮弹为例,采用hp-RPM方法设计了带落角约束方案弹道。导弹的质量为50.31 kg,参考面积S=1.327×10-2m2,发射的初速度v0=400 m/s,投放坐标(x0,y0)=(0 km,20 km),弹道倾角θ0=0 rad,攻角α0=0 rad。该型号导弹部分气动参数如表1所示。 表1 气动参数 表2 终端约束 实验结果如图1~图6所示。根据传统最大升阻比法可计算得到相同发射条件下,该型号导弹的最大射程为7.526×104m,由图1~图3,在导弹最大射程范围内,hp-RPM方法适用于以不同落角精确打击不同距离处地面静止目标的优化弹道设计,同时能满足飞行过程中的过载限制。 图1 不同终端约束下基准弹道的轨迹曲线Fig.1 Trajectory curve of reference trajectory under different terminal constraints 图2 不同终端约束下基准弹道的弹道倾角曲线Fig.2 Trajectory inclination angle of reference trajectory under different terminal constraints 图3 不同终端约束下基准弹道的过载曲线Fig.3 Overload of reference trajectory under different terminal constraints 控制系统在导弹的滑翔段操纵舵翼偏转,实现对飞行姿态的有效控制,图4为理想状态下基准弹道的舵偏角的变化曲线,由于实验中以最短滑翔时间为性能指标,故舵翼在进入滑翔段后立刻充分偏转,使导弹获得较大攻角,极大减缓导弹速度的衰减速度,使导弹按较小的弹道倾角和较大速度迅速逼近目标,达到短时间内击中目标的目的。在滑翔段的中期,舵偏角变化平缓,有利于方案弹道的实现。由于对弹道末端的落角存在约束,在导弹接近目标时,舵翼产生反向舵偏角,使弹头向下倾斜,从而获得较大落角,如图4~图6所示。 图4 不同终端约束下基准弹道的舵偏角曲线Fig.4 Rudder deflection curve of reference trajectoryunder different terminal constraints 图5 不同终端约束下基准弹道的速度曲线Fig.5 Velocity curve of reference trajectory under different terminal constraints 图6 不同终端约束下基准弹道的攻角曲线Fig.6 Attack angle curve of reference trajectory under different terminal constraints 假设导弹的升力系数和阻力系数由于模型误差的存在±10%的波动,且导弹在发射后50~100 s内受0~50 m/s的阵风干扰。导弹的发射条件和路径约束与4.1节中的实验相同,终端约束为αf=-85°,定点打击坐标位于(60 km,0 km)处的静止目标。分别采用开环控制和本文提到的闭环制导方式进行仿真实验,硬件环境为Core i7处理器,16.0GB RAM,软件环境位64位Win10操作系统,Matlab R2018a软件,实验结果如图7~图10所示。 图7 开环和闭环控制下的弹道轨迹Fig.7 Trajectory under open-loop and closed-loop control 图8 开环和闭环控制下的速度曲线Fig.8 Velocity curves under open and closed loop control 图9 开环和闭环控制下的弹道倾角曲线Fig.9 Trajectory inclination curves under open-loop and closed-loop control 图10 开环和闭环控制下的过载曲线Fig.10 Overload curves under open and closed loop control 由实验结果可知,相比于阵风影响,±10%的气动参数波动对弹道各项参数影响不大。若采用开环控制,将离线设计的最优控制律u0直接应用于控制系统,导弹在50~100 s间由于受到阵风影响,将明显偏离基准弹道,弹道倾角显著减小,导弹提前击中地面,无法准确命中目标。 表3中为开环控制和闭环控制仿真实验的终端参数,发现由于模型参数误差和阵风干扰的存在,使开环控制下的导弹在终点时刻,与目标水平相距1.977 km,且落角为-23.23°,不能满足作战需求。若采用基于hp-RPM的闭环制导方式,则导弹在终点时刻的位置横坐标为59 981.06 m,与目标近相差18.94 m,打击精度得到很大提高,能满足一般作战需求。闭环制导下的实际弹道落角为-85.46 °,飞行时间为202.23 s,与基准弹道的落角和滑翔时间相差不大,基本可以实现预设的快速、大落角、精准打击的作战指标。 表3 开环和闭环控制下的终端参数 采用hp-RPM方法设计在不同作战指标下的制导炮弹滑翔段的方案弹道和在线制导策略。通过仿真实验分析了滑翔弹最短滑翔时间和落角控制的作用机制,证实了基于hp-RPM方法的闭环在线制导策略能有效抑制模型误差和外部扰动,实现既定的作战指标。由于系统的控制周期由程序优化计算时间决定,所以对误差的抑制能力与计算机的计算能力相关。 本文中的研究结果可为滑翔制导炮弹制导律设计提供参考,具有工程应用价值。4 基于hp-RPM的在线制导策略
5 仿真实验结果
5.1 方案弹道实验

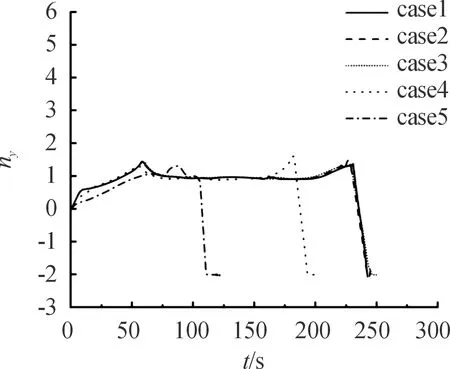
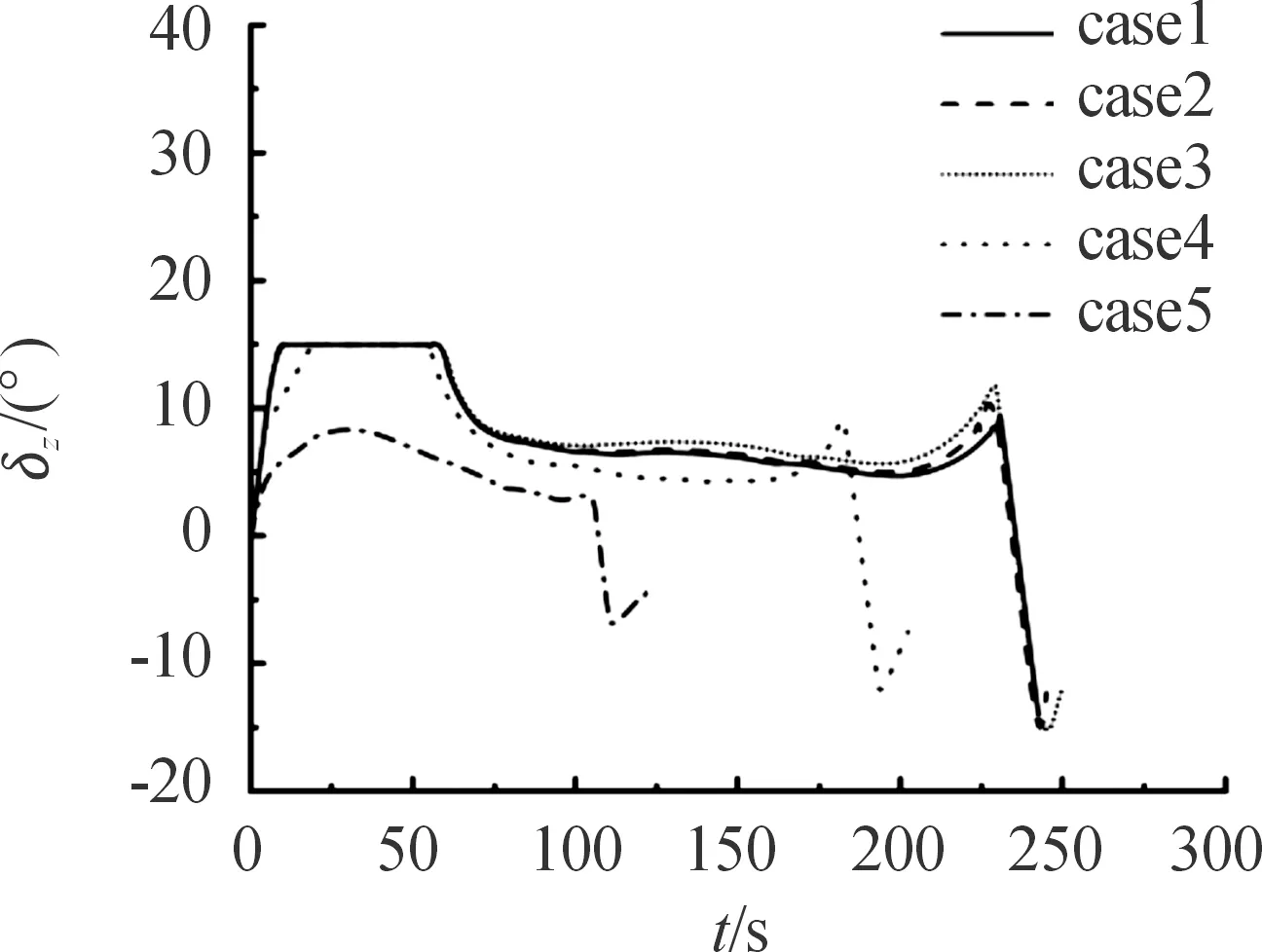
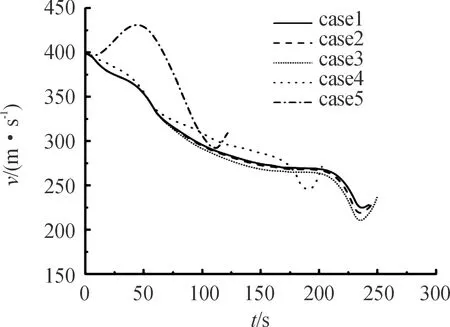
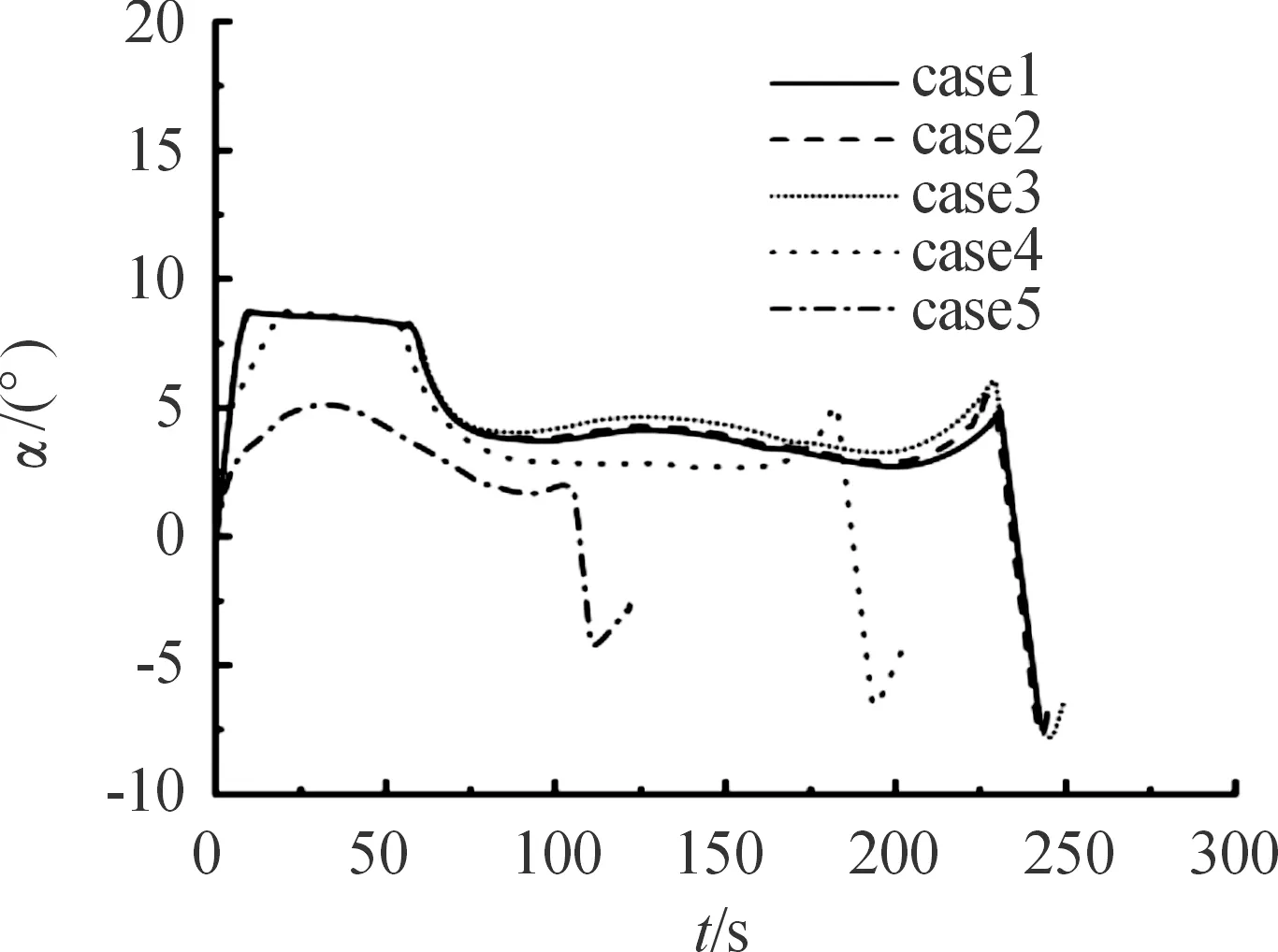
5.2 滑翔弹道再入制导

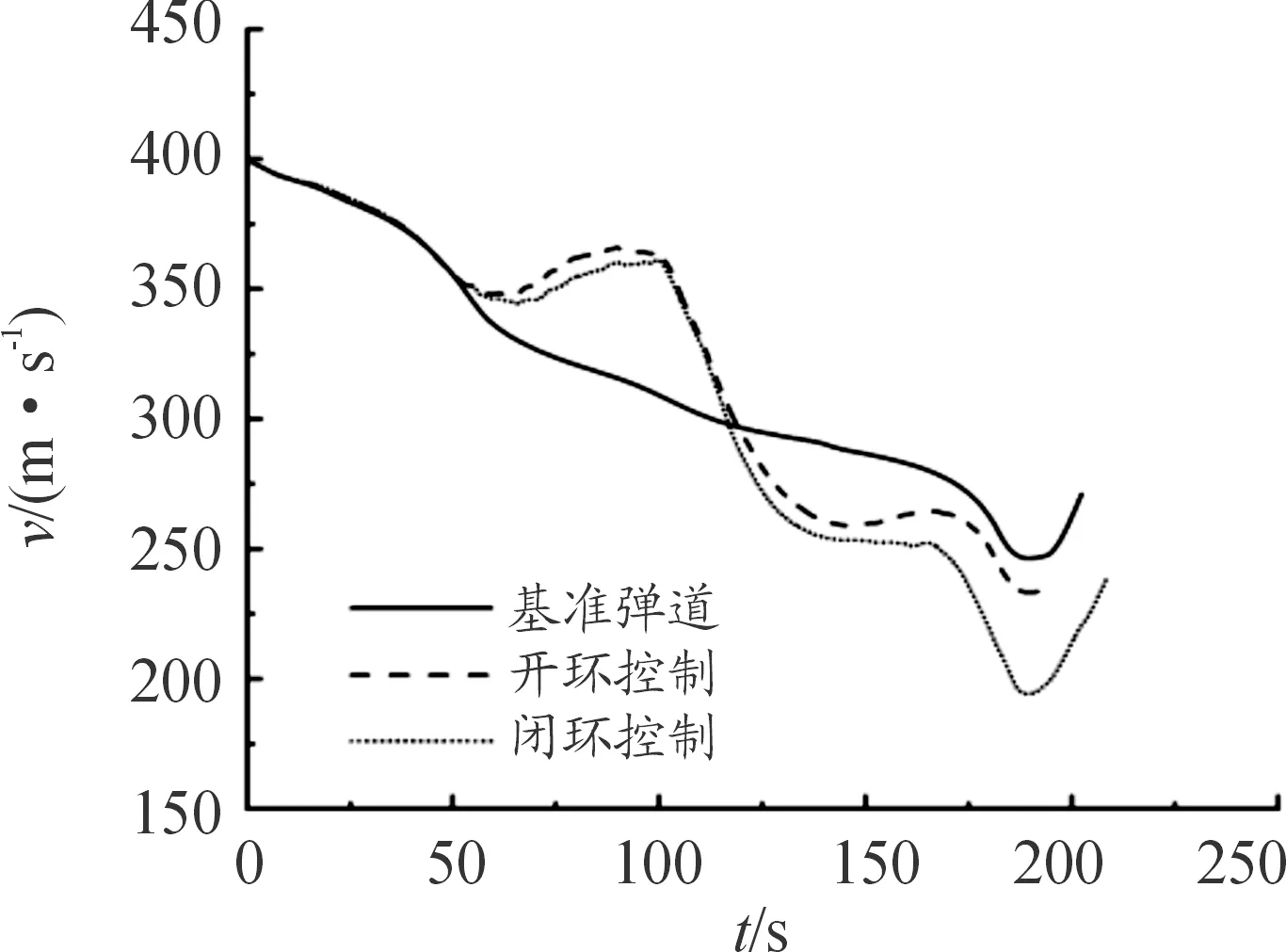
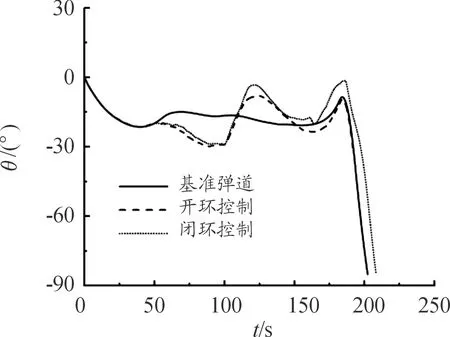

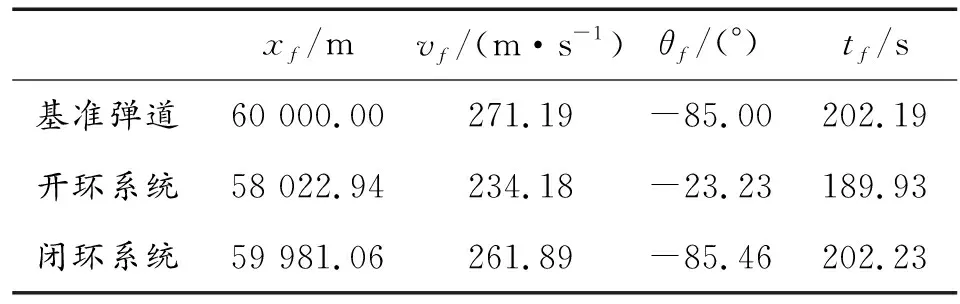
6 结论
