基于振动频率与自适应模糊神经网络的索力计算研究
2021-10-15陈跃华宁波大学海运学院浙江宁波315211
王 振 闫 伟 张 刚 陈跃华(宁波大学海运学院 浙江 宁波 315211)
0 引 言
斜拉索是斜拉桥的主要受力构件,索力的准确测量不仅关系到桥梁工程能否安全实施,更影响到建桥后主梁、主塔的线形是否符合工程要求。因此,准确测量拉索索力是研究学者及桥梁建设者共同关注的问题。目前,对于拉索索力的测量方法包括振动频率法、传感器测量法、垂度测量法、拉索静态线形测量法等。振动频率法实测拉索的固有频率,利用索的张力和固有频率的关系计算拉索索力;传感器测量法通常采用压力传感器测量索力,需要在每根拉索上安装压力传感器,经济成本过高;而垂度法是依据拉索测量段的倾斜角、索长和最大垂度推导出的索力公式计算拉索的平均索力值,考虑索力差值和索段位置来确定整个拉索的索力。因此,频率法测量索力仍然是最为经济实用且测量较为准确的方法[1-5]。
基于频率法来测量索力,主要是利用数据采集仪器测量斜拉索的振动频率,再建立拉索频率与索力之间的函数式,从而由频率计算出拉索索力[6-9]。Ren等[10]基于能量法以及数据曲线拟合方法,考虑抗弯刚度和垂度对斜拉索振动特性的影响,推导出可以计算斜拉索的索力公式,并主要考虑一阶频率进行研究,采用基频来计算其索力。Fang等[11]基于拉索的横向振动理论知识,采用曲线拟合技术,避免了采用迭代法求解非线性方程,得到了求解索力的实用公式,但该索力公式只考虑了抗弯刚度影响,忽略了拉索垂度作用的影响。Sun等[12]建立了灵活约束条件下拉索索力实用计算模型,提高了弹性约束条件和抗弯刚度下的拉索索力求解精度。Ma[13]提出了一种精确确定边界条件未知的斜拉索张力的方法,该方法可以同时识别弹性边界条件下的多个参数。但在实际应用中影响拉力的因素过多,在较为准确计算、检测频率的基础上,需要对基频-索力函数关系进行修正。甘泉等[14]基于斜拉索横向振动方程的通解,通过在弦振动理论公式的基础上,引入刚度修正系数,并且提出了可用于两端固支条件下的拉索索力计算的统一公式。Sun等[15]针对求解过程中忽略边界条件及抗弯刚度对拉索的索力精度的影响,提出计算修正公式。Dan等[16]基于数值模拟方法对张力误差进行研究,并给出了经验误差修正公式用来拟合索力误差之间的关系。
综上,基频的准确计算与测量、频率-索力求解方程的正确修正是索力测量的关键问题。本文考虑弹性边界条件并基于弦振动原理与切比雪夫级数方法建立频率与索力之间的函数关系,并利用自适应神经模糊网络与实验数据结合的方式,修正频率-索力关系式以保证索力的准确计算及测量。
1 弹性边界下拉索的频率特性及索力切比雪夫级数求解
1.1 弹性边界下拉索的频率特性求解
本文将任意边界条件等效为拉索的左右两端分别连接拉伸约束弹簧K1和K3、扭转约束弹簧K2与K4,建立的弹性边界条件拉索振动模型如图1所示,其中L为拉索的长度。
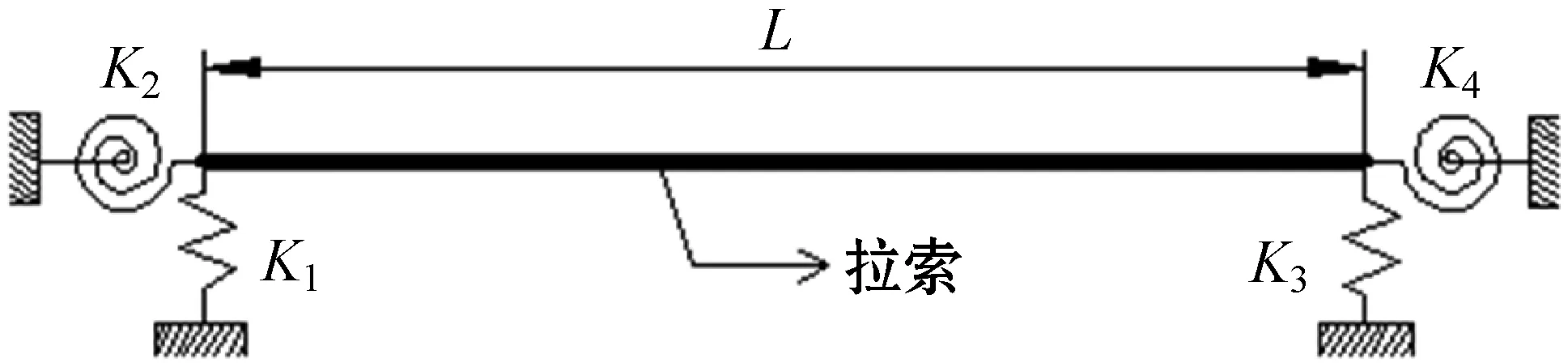
图1 弹性边界条件下拉索振动模型
通常,拉索的振动微分方程可表述为[17]:
(1)
式中:EI为拉索抗弯刚度;T为拉索索力;ρΑ为拉索线密度;u(x,t)为拉索振动位移函数。则拉索的弹性边界约束表述为:
(2)
式中:k1=K1/EI,k2=K2/EI,k3=K3/EI,k4=K4/EI。
基于分离变量法,将拉索振动函数分解为时间序列函数与振型函数Y(x)的乘积:
u(x,t)=Y(x)sin(ωt+φ)
(3)
式中:ω为拉索固有频率;φ为相位角。将式(3)代入式(1)可得:
EIY(4)(x)-TY″(x)-ρAω2Y(x)=0
(4)
式(4)为振型函数的微分方程,将振型函数采用切比雪夫级数[18]进行展开,设:
(5)
式中:ai为待定常数。式(5)中切比雪夫级数为:
将上式代入振动函数式(3),为使振动函数满足边界条件,构造辅助函数h(x)和g(x)分别为:
(6)
式中:
若令:
Φi(x)=h(x)Ti(x)+g(x)
(7)
则满足边界条件式(2)的振型函数为:
(8)
由式(8)给出的振型函数不是式(4)的真实解,因此代入式(4)时,式(4)并不等于零。但根据虚位移原理,可以使其在虚位移上所做的功为零,即:
(9)
展开可得:
(10)
由于δaj是任意的,整理可得频率方程为:
(11)
式中:
写成矩阵的形式:
|D-ω2Ms|=0
(12)
显然,求解矩阵形式的频率方程式(12),得到对应的特征值与特征向量,即可得到振动系统前n阶的固有频率。
1.2 弹性边界条件下拉索的索力计算及分析
考虑图1所示拉伸约束与扭转约束共同作用弹性边界条件下,推导拉索索力-频率计算公式。根据所得计算公式,简化边界条件,进一步推导固支和铰支条件下索力计算公式。
为求解弹性边界条件下的索力计算公式,设振动函数解如下:
u(x,t)=Y(x)ψ(t)
(13)
ψ(t)=A1sinωt+A2cosωt
(14)
Y(x)=a1sinαx+a2cosαx+a3sinhβx+a4coshβx
(15)
式中:ψ(t)为时间序列函数;Y(x)为振型函数;a1、a2、a3、a4为待定系数;ω为索自振频率。α和β计算为:
(16)
将式(15)振型函数代入式(2)可得一般边界条件下拉索的频率-索力表达式:
(17)
欲使式(17)有非零解,则其方程组系数行列式应为零,即可得:
(18)
将式(18)简化计算处理得到:
(19)
式(19)为一般边界条件下索力-频率的关系式。显然,若将拉索边界条件简化为简支-固支,则式(19)会大大简化,可得出弹性边界条件下简化的索力表达式。
若拉索为简支约束条件,此时K1=K3=0,K2=K4=∞,则式(19)变为:
(EI)2(α2+β2)2sinαLsinhβL=0
(20)
显然,(EI)2(α2+β2)2和sinhβL不为零,因此有sinαL=0,即:
αL=nπn=1,2,…,n
(21)
将式(21)代入式(19)且忽略抗弯刚度影响,可得两端简支边界条件下拉索的频率与索力之间的关系式:
(22)
式中:L为拉索的长度;fn为第n阶自振频率。
若拉索为固支约束条件,此时K1=K3=K2=K4=∞,若省略式(19)中边界条件的低次项,整理式(19)可得:
2αβ[1-cos(αL)cosh(βL)+(α2-β2)sin(αL)·
sinh(βL)]=0
(23)
由于式(23)是一个超越方程,不能直接得到索力-频率的关系式。根据文献[19]中的超越方程求解方法并且忽略抗弯刚度对拉索的影响,可得索力-频率的关系表达式:
(1) 当使用第一阶振型的固有频率时:
(24)
(2) 当使用第二阶振型的固有频率时:
(25)
(3) 当使用第高阶(三阶及以上)振型的固有频率时:
(26)
显然,简单边界条件下索力计算公式是弹性边界下索力计算公式的简化。而且弹性边界下索力公式计算复杂,弹性边界参数往往不可得,因此在计算拉索频率与索力之间的表达式时存在很大难度。一般国内外学者对斜拉索的索力计算公式均将弹性边界约束条件下的索力表达式写成对简支公式乘以修正系数,即:
(27)
式中:Δ为修正系数。在理论计算中,弹性边界条件下的索力计算公式的修正系数很难求解得到,需要依靠实验数据来确定Δ的大小。因此,本文采用自适应模糊神经网络拟合实验室数据方式对式(27)进行修改。
2 实 验
2.1 数频率特性实验验证
基于前面的理论部分的公式和结论,在实验室搭建拉索振动实验平台来验证,左右两端采用2个基座用地脚螺栓连接固定在地面上,拉索两端采用螺纹卡扣进行固定。利用激励力锤作用于拉索某一位置获得其振动数据信号,通过在L/4索长处安装压电式加速度传感器(YBY-10KN型)测量振动信号。拉索的张紧力采用拉压传感器测量,拉索张紧力采用数据采集器(东华测试技术有限公司DH3820型)进行数据采集,拉索振动模态测试采用采集器(DH5922型)进行数据采集。将采集仪采集到的振动信号传输到连接好的电脑上,通过软件进行分析,测试仪器及分析软件如图2所示。

(a)
(b)图2 DH3820型采集器及分析软件界面
实验对象选择型号304不锈钢拉索,拉索的基本参数如下:拉索单位长度质量m=0.081 kg·m-1,拉索直径d=4 mm,拉索弹性模量E=1.93×108Pa,拉索截面惯性矩I=1.257×10-11m4,T=3 960 N,拉索长度L=6.8 m。分别在两端固支和两端固支-简支两种边界条件下进行实验。
表1给出了两端固支边界条件下实验结果与本文频率特性求解方法得到的计算结果前十阶固有频率进行对比分析的结果。可以看出,其最大相对误差为3.388%,最小相对误差为-0.989%。
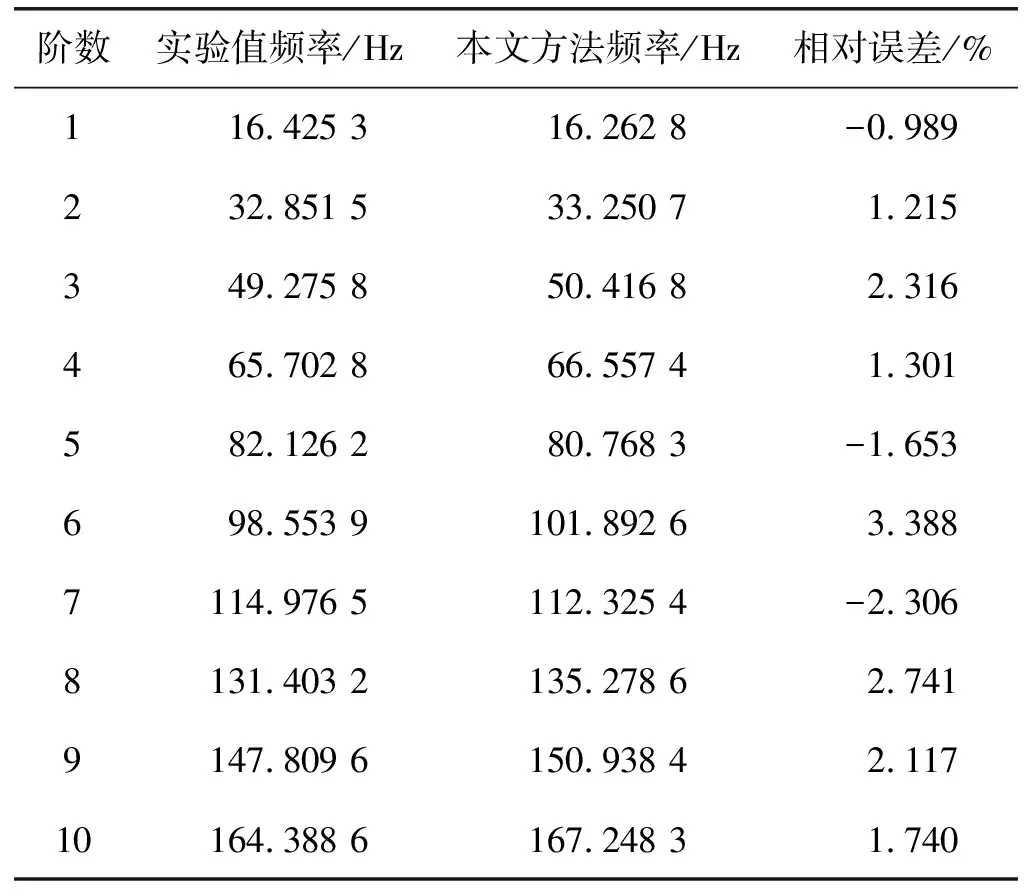
表1 固支-固支边界条件下拉索固有频率
表2给出了固支-简支边界条件下实验结果与本文频率特性求解方法计算结果前十阶固有频率进行对比分析的结果。可以看出,最大相对误差为3.284%,最小相对误差为0.709%。通过对比分析再次验证本文边界模拟方式与理论模型的正确性。在两种边界条件下估算出的Tmin均为3 780 N,Tmax均为4 210 N,索力相对误差均为-4.545%-6.313%,由此可见本文方法可用于有效估算拉索索力。
通过搭建拉索振动实验平台,在两端固支和两端固支-简支这两种边界条件下对拉索进行模态实验,与计算结果进行对比,其相对误差小于3.388%,表明本文方法在计算弹性边界条件下拉索振动模态是有效的,为后续拟合基频-力的关系提供较为准确的理论依据。
2.2 索力自适应神经模糊网络修正及实验验证
理论上可以利用基频求解拉索索力,但是存在如下问题:(1) 拉索的索力计算公式没有具体统一的形式,应用条件限制较多。(2) 为简化索力计算公式,通常忽略抗弯刚度及垂度的影响,造成理论上很难保证计算的索力精确度。(3) 为提高索力计算精度,通常会在索力计算公式中添加补偿项,计算形式较为复杂,很难进行工程应用。从上文推导频率-索力计算公式中也可以看出,计算公式比较复杂,在计算过程中忽略较多因素(如抗弯刚度、索力增量等),因此降低了索力的求解精度。弹性边界一般在实际应用中难以确定,导致索力求解难度增大。因此,对于基频法求解拉索的索力时计算公式存在的问题,可以利用自适应神经模糊网络结合实验数据的方式,在较为准确计算和测量基频情况下,采用实验方法(在一定条件下)来拟合基频-力关系。
通过对自适应神经模糊网络方法的学习和实践,学习到自适应神经模糊网络(ANFIS)最大的优点是基于I/O数据驱动的建模而不需要建立实际的理论模型,通过数据学习逼近,最后更加逼近于实际数据输出。该方法不是通过经验得来的,因此对于那些认识还存在模糊不清晰或者是非常复杂的系统,应用自适应神经模糊网络的方法,通过获取实际数据,再进行数据学习逼近输出,该方法具有的优势显得尤为突出。本文采用五层结构ANFIS,其示意图如图3所示。
第一层为输入层,设有三个输入:拉索长度L、拉索基频w、拉索单位质量m。
第二层为输入变量隶属度函数层,对于第j组训练数据对(Lj,wj,mj),数据训练前采用高斯函数进行输入函数的模糊化,即:
(28)
式中:i表示模糊子集数;cij、σij分别表示隶属度函数的中心和宽度。
第三层为规则层,进行模糊运算,输出各神经元输入取积后的归一化值,即各条规则的激励强度归一化,各节点输出为:
(29)
第四层为自适应运算层,该层结合27条控制规则完成自适应运算计算出每条规则的输出,节点结果输出为:
(30)
式中:pi、qi、ri(i=1,2,…,27)是该节点的结论参数。
第五层为输出层,其结果为自适应运算层中各节点之和:
T=C1+C2+…+C27
(31)
在第四层与第五层中,使用最小二乘法单独辨识结论参数可省掉求导的过程,相比梯度法效率更高。因此ANFIS将最速下降法与最小二乘法结合用来调整网络参数。
2.3 实验设置及结果
搭建拉索振动实验平台,搭建方式与2.1节中弹性边界条件下频率特性实验相一致。利用激励力锤作用于拉索获得其振动信号,通过在1/4索长处安装压电式加速度传感器测量该位置处的振动数据信号,再将采集仪采集到的振动信号传输到电脑中,通过软件对测量的数据进行分析,拉索的索力测试系统如图4所示。实验对象选择型号304不锈钢拉索,其基本参数与拉索频率特性求解中的参数一致。

(a)

(b)图4 拉索的索力测试系统
本文中的数据为实验实测数据,其中用于仿真研究的训练数据及测试数据如表3所示。分别测得不同长度和不同索力下的拉索的频率,从而利用自适应神经模糊网络来进行仿真研究频率和索力的关系。
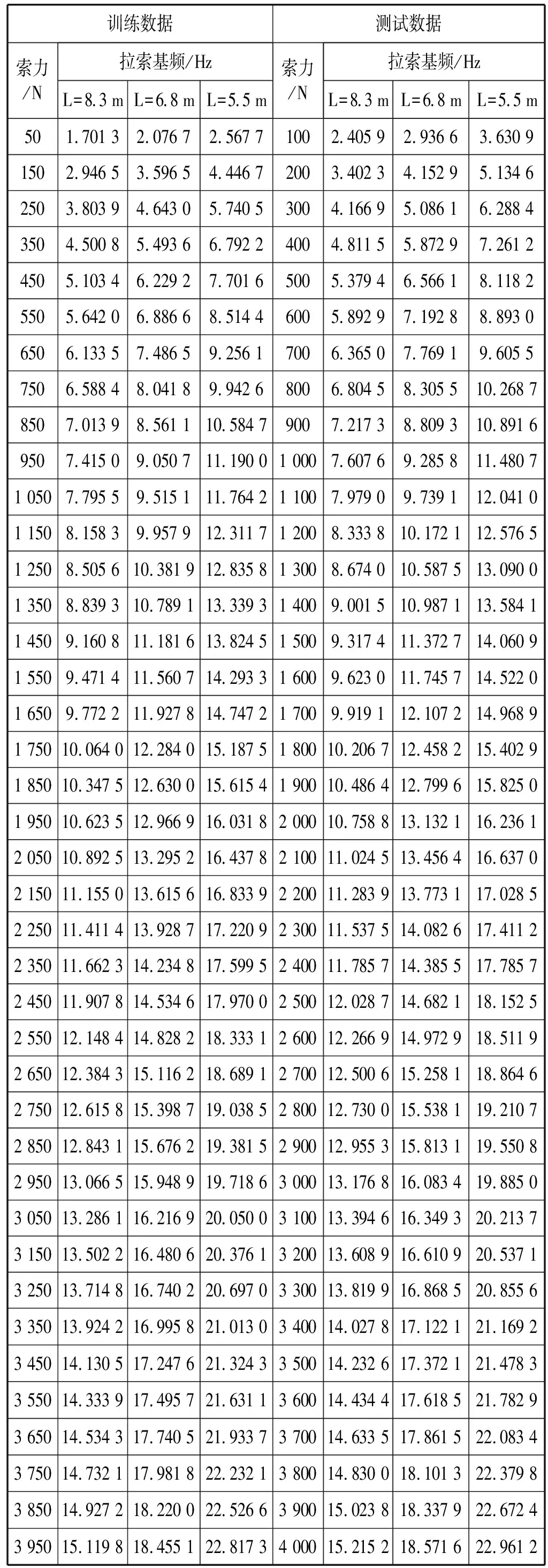
表3 拉索的索力训练数据及测试数据表
利用MATLAB中提供的自适应神经模糊推理系统的图形用户界面编辑器(Anfis Editor),将实验测得的数据分别加载到编辑器中的训练数据和测试数据中,通过网格分割法自动生成自适应神经模糊推理系统。在索力计算中,神经网络的输入参数为3个,即:拉索长度,拉索基频,拉索单位质量。为实现自适应神经模糊系统的推理功能,输入的3个参数对应的模糊隶属度函数数目设定为3,模糊隶属度函数类型设定为钟型。生成初始的模糊推理系统后本文选择优化方法为混合算法,训练次数为40次。
搭建的实验平台可靠性及准确性在上一部分中已得到验证。为验证本文方法的正确性与有效性,保证本次实验测得数据的可靠性及准确性。分别在两端固支和固支-简支两种边界条件下进行仿真实验,图5为两种边界条件下拉索基频与索力关系图。
实验数据经过40次对自适应神经模糊系统的训练及测试后,可得训练模糊推理系统及测试模糊推理系统的误差,图6为自适应神经模糊推理系统的训练结果及训练误差,训练平均误差达到0.138 92 N,相对误差为0.003 47%。
图7为自适应神经模糊推理系统的测试结果,平均测试误差达到0.291 1 N,相对误差为0.007 27%,结果理想。
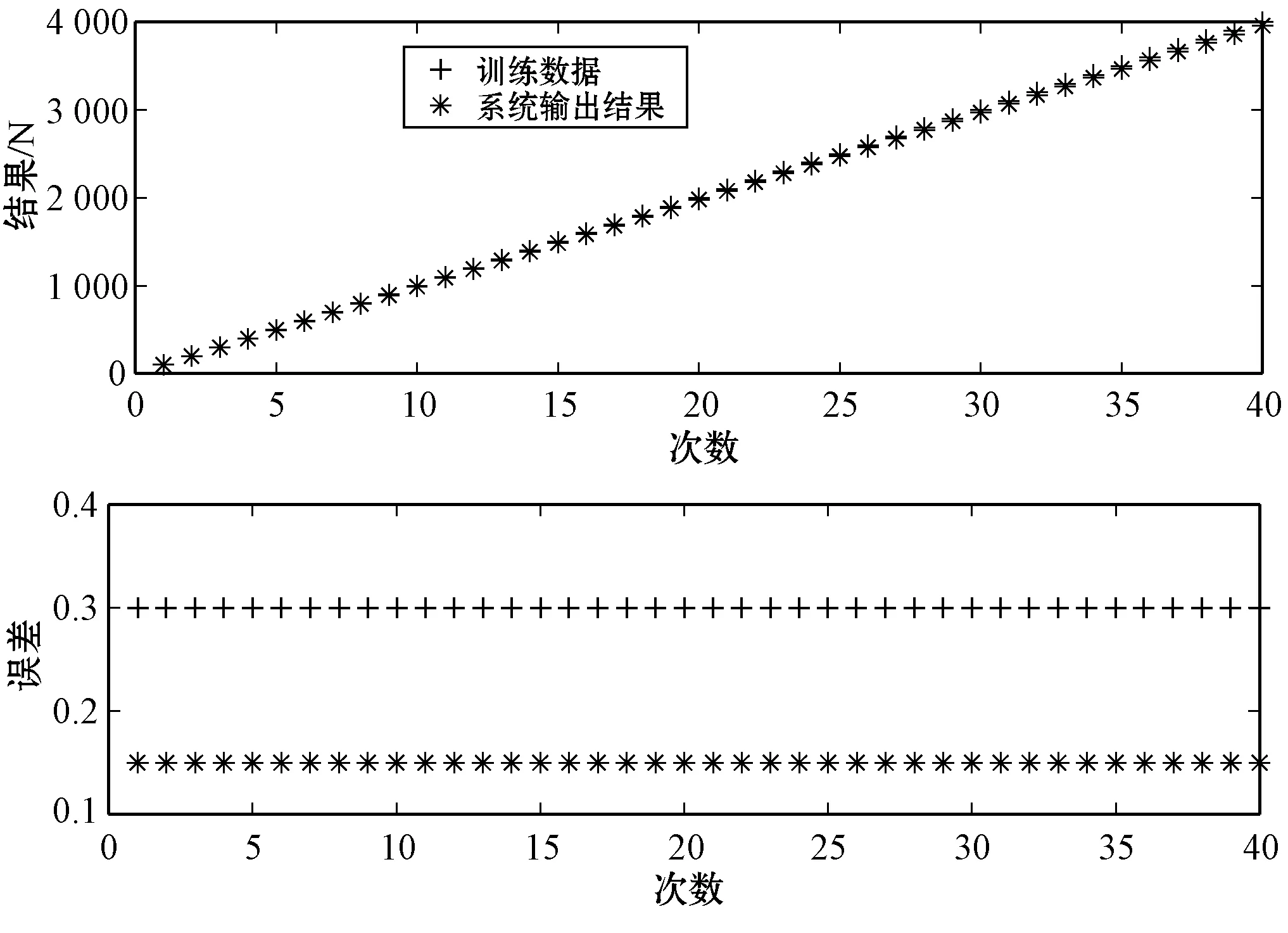
图7 自适应神经模糊推理系统的测试结果和测试误差
通过上述分析可以得出,本文设计的自适应神经模糊推理系统可以保证推理系统的准确性。实测实验数据与自适应神经模糊推理系统相结合,提高了拉索基频与索力关系的精确度,减小了因理论模型误差、计算公式误差等带来的索力计算精度无法满足工程需要的不良影响。
3 结 语
(1) 基于弦振动原理,分析了更加符合实际工程要求的拉索边界,建立频率与索力之间的关系函数,利用实测实验数据与拉索基频相结合的方法,求解拉索基频与索力的关系,提出的索力计算方法及研究结果可以为工程应用中的索力估计提供有效的解决途径。
(2) 以实测实验数据为基础,自适应神经模糊系统结合基频-索力求解公式推理出拉索基频与索力的关系,简化了拉索理论数学模型建立的复杂度及繁琐的索力计算公式。
(3) 经过自适应模糊推理系统得到的训练平均误差在0.138 92 N,测试误差达到在0.291 1 N,相对误差分别为为0.003 47%和0.007 27%。表明拉索基频与索力关系的准确度较为理想,也表明本文方法能达到工程应用中计算索力的要求。
