时空图法解运动介质表面的反、折射问题

许广智，李一杰

(辽宁大学 物理学院，辽宁 沈阳 110036)

各向同性均匀介质运动后显现各向异性，光在其中传播时波法线(波矢)方向与光线方向分离，具有独特的反、折射规律及频移关系[1-7].利用边界关系结合几何方法[1]、四维波矢量协变关系[2-5]等均可对此开展研究.文献[7]给出用介质静止系中角度参数表示的任意角入射情况反、折射中频率、波矢量、光速矢量的普遍公式，可以应用不同参考系中角度变换公式将公式转化为实验室系下可测量表示，但较为繁琐.本文应用时空图法研究光以任意角度入射到介质表面沿光线方向的反、折射规律及其相对入射波的频移，易得到可测量表示的结果.

1 应用时空图进行解析求解

两介质相对S系以速度v共同运动，其界面法线(单位矢量n)与v夹角为αn，以v方向为x轴正向，建立右手坐标系，使得n在xOy平面中，即n=(cosαn,sinαn,0).入射、反射、折射光线所在方向的单位矢量ni、nr、nγ由各自方向余弦定义为nq=(cosαq,cosβq,cosγq),q=i、r、γ.介质固联的S′系中，用带撇符号定义相对应的量.S′系坐标原点在界面上,t(t′)=0时刻，与S系坐标原点重合.S′系中，界面两侧介质内各向光速相等，入射、反射光速为v1，折射光速为v2，界面处光线遵循一般的反、折射定律，反、折射光线所在方向单位矢量满足

(1)

反、折射单位矢量各分量大小由此写出

(2)

n、n′分量间大小关系由x方向尺缩关系得到

(3)

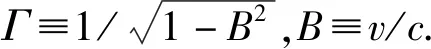
t(t′)=0时刻，光线由原点位置入射.四维时空图下，此入射光线(光子)在S′系-cΔt′时刻的时空坐标对应事件点a，经界面反射、折射后，cΔt′时刻反、折射光线(光子)所处时空坐标分别对应事件点d、f.仅需要绘制xOct(x′Oct′)面的二维时空图(图1)，A、D、F分别是a、d、f在此面的投影点.OE是入射点处界面的世界线，也是S′系中时间轴ct′，OC是x′轴，OE//AC//DI//FJ，有∠EOct=∠COx=∠BOC=∠HDI=∠GFJ=η，tanhη=B，coshη=Γ.AO、OD、OF分别是入射、反射、折射光子世界线在xOct面的投影，AC=DI=FJ=cΔt′.随着介质界面与运动方向夹角变化，D、F将在FD线上移动.

图1 xOct(x′Oct′)面投影的反、折射过程二维时空图

S系中，光速各向异性，入射、反射、折射光速vi、vr、vγ待求.如图中定义ξ、τ、ζ角，根据A、D、F三点处几何关系可列出对应入射、反射、折射过程的3个方程组[8].注意到

Δy=Δdcosβ=Δttanhηcosβ,

这里Δyi对应a世界点y(或y′)坐标大小，则写出入射部分方程如下式

(下文中定义Bq≡vq/c,q=1、2、i、r、γ)

(4)

(5)

(6)

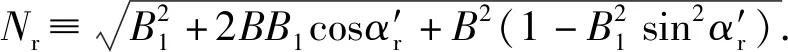
低速(B→0)情况下,得到近似结果如下：

(7)

其中

(8)

式(7)中第一式光速一级修正中负号来源于入射光方向与ni定义反向.反射的一级修正使得光线方向向界面法线方向偏移.折射的一级修正较复杂，除了入射面上光线方向偏移外，还有向介质运动方向的偏移.

2 数值结果

为考察介质运动速度、界面角度、入射角度对反、折射光线方向的影响，选取不同参数绘制图2.图2(a)-(e)对应反射过程，(f)-(j)、(k)-(o)分别对应光疏到光密(以下简称疏密)、光密到光疏(以下简称密疏)的折射过程，3组过程分别选取5种情况,界面法线与介质运动方向(图中用箭头标出)夹角αn=0、π/4、π/2、3π/4、π.反射、密疏折射入射角选为θi=π/6，疏密折射入射角选为θi=π/3.每图中φi=0、3°、6°、…、357°(φi是以n为轴方向建立球坐标系的方位角)，绘制入射、反(折)射光线(图中仅显示入、折射光线上与坐标原点距离1的点，反射光线与原点距离1.2的点，相应光线可由这些点与原点连线得到.用i标记入射，用B的数值来标记不同介质运动速度时的反、折射).具体参数选取详见图中标注.

图2 不同参数对反、折射光线方向影响(a)—(e)对应反射过程，(f)—(j)、(k)—(o)分别对应光疏到光密、光密到光疏折射过程.

除αn=0、π或φi=0、π之外，一般情况下，S系中的反(折)射光线不在由入射光线及界面法线确定的入射面上.αn=π/2(界面精确平行介质运动方向时)的反射过程与静止时有相同的反射定律，反射光线方向不随介质运动速度变化.随着介质运动速度的提高，反射光线及疏密折射光线的方向总体上向介质运动方向趋近，密疏折射光线方向向介质运动方向(αn>π/2)或反方向(αn≤π/2)趋近.高速情况下，随着速度持续提高，一定角度的反射光线方向大幅变化，先远离再趋近介质运动方向(参见图2(d)中B=0.6→0.85)；密疏过程中，一定角度范围内不发生折射.从具体表达式可知，在极限情况下(反射B→B1,B1→1，折射B→1)，所有反射、疏密折射光线沿介质运动方向，密疏折射光线沿运动方向(αn>π/2)或反方向(αn≤π/2)(极限速度下，密疏过程消失的折射再次出现).

3 反、折射中的频移

利用文献[8]中的方法，通过时空图法可求出运动介质中沿光线方向的多普勒频移公式为

(9)

这里θ是S系中光线出射方向与运动方向夹角.注意到S′系中，反、折射过程不发生频移，利用前文的结果可得到用可测量表示的频移公式.低速近似下，有

(10)

(11)

反射过程发生在真空中的特殊情况时，有

BΓ2[4cosαicos2αn+2Γ-2sin2αncosβi+

B(2-Γ-2)cos2αn]}

(12)

如将入射光线限定在xOy面(界面法线与介质运动方向共同确定平面)上，可验证调整为文献[4]相同的参数设置后与其结果一致.

4 结语

光入射到运动介质表面出现各向异性的反、折射特性来源于光在介质中的光行差.波矢方向与光线方向具有不同的光行差公式，导致它们有不同反、折射特性(比如折射过程中αn=π/2时，与光线方向的折射规律不同，波矢方向遵循静止时的折射定律[3]).光行差公式的差异源于介质中波矢(k0,k)是类空矢量，光线方向速度矢量Γ(c,u)是类时矢量，有k0/|k|=|u|/c.此时，对于运动介质中反、折射过程中波矢方向的求解，只需要将式(4)—(6)中Bq→1/Bq,q=1、2、i、r、γ，对于光行差公式也是如此.

感谢石薇、张成园老师对相关问题的有益讨论.