基于路径形态学和正弦函数族匹配的电成像测井缝洞自动识别与分离方法研究

王磊 ，沈金松 *，衡海亮 ，魏帅帅

1 中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249

2 中国石油大学(北京)CNPC物探重点实验室，北京 102249

0 引言

碳酸岩盐储层在各种类型的岩性储层中的占比较大，从已公布数据来看，碳酸岩盐储层的开采产出可达全球范围内油气产出的六成左右[1-4]。该类型油气藏裂缝较发育，因此对缝洞型碳酸盐岩储层的研究至关重要。该类型储层的油气主要存在交错的裂缝、经风化腐蚀和流体经过形成的孔洞之中，其构成成分有原生基质孔隙及次生裂缝、溶孔、溶洞[5]。孔隙型、溶洞型、裂缝型为基本储集类型，孔洞型、缝洞型、孔缝型、孔缝洞复合型为过渡类型[5-6]。正是由于缝洞型储层的复杂性，缝洞的测井识别与评价仍存在多方面的难题，例如，缺乏储层类型准确识别和划分有效方法，缺少储集空间定量表征的高精度方法。因此，实际生产亟需研究缝洞自动识别与分离算法。

缝洞型储层并非今天才进入人们的视线。李瑞、陆云龙等通过井口直径的计算方法结合RLLD/RLLS理论，归纳出裂缝出现的可能性的值，并以此作为储层含油性评价的标准[7-8]。杨辉廷等利用测井及钻井数据对塔里木盆地裂缝和溶蚀孔洞信息进行了较为准确的计算，对与水平地层呈不同角度的裂缝进行了提取，对孔洞饱含油、气、水的分类通过自然伽马算法进行了划分[9]。陈科贵等从岩层内电流经过缝洞和非缝洞部分的串并特征进行分析，试图以此来计算岩层的渗透率，并认为岩层的渗透率不是一成不变的[10]。

电成像测井对碳酸盐岩缝洞型储层的评价作用在油气业界逐渐获得越来越多的关注，国内外学者和油气服务公司发表了许多成果。为了将裂缝和孔洞从基质中区分开来并计算获得参数，斯伦贝谢公司的Delhomme首先发表了成像的阈值法，这可以将缝洞的外形显示出来，同时指出裂缝所在深度段[11]；Hall等尝试使用Hough变换计算正弦型的裂缝信息和地质走向数据，就符合正弦分布的连续裂缝取得了较好效果[12]。景建恩等针对塔河油田碳酸盐岩储层的裂缝，通过对FMI测井图像数据使用R型聚类算法，建立了裂缝指标数据集合，并对裂缝出现可能性做出了客观评价[13]。李曦宁、李振苓和沈金松等提出了基于二值图的完备路径形态学算法，用于分离地层层理与裂缝[14-15]。除此之外，人工智能算法在测井领域的应用实例也越来越多[16-22]。针对电成像测井，XUEYongchao等[19]利用遗传算法与神经网络结合对多种测井资料进行处理进而实现裂缝识别。Azim[20]提出一种鲁棒性高的神经网络算法(ANN)，利用Fortran语言建立以后向传播为基础的训练过程，引入5口井的微电阻率成像及传统测井曲线数据的80%作为训练集，20%作为测试集，以此来估计裂缝密度和分形两个维度上的裂缝性质，预测储层段井壁附近的三维裂缝分布图。李冰涛等[21]提出基于TensorFlow的图像语义分割模型DeepLabv3+来对经由Labelme工具标定后的裂缝数据进行像素分割和提取，效果较好。邹文波对人工智能在岩性识别、低电阻率油层识别、储层参数评价、储层裂缝孔洞识别等4个测井重点方向的研究现状进行了分析和总结[22]。然而，由于受复杂地质环境和井孔干扰的影响，电导率图像的缝洞自动识别和定量评价仍存在诸多困难，例如受地层或极板切割的裂缝或孔洞因为其不连续性，对其进行定量评价仍较为困难。

本文根据数学形态学基本理论和不完备路径算子适应于弯曲线性结构追踪以及对间断有较强容忍度的特点，将不完备路径形态学算法、正弦函数族算法和二阶矩椭圆拟合算法应用于电导率测井图像，通过给定长度的路径算子、容忍算子和正弦函数族数据集完成对裂缝参数的准确计算，形成了一种不完备路径形态学算法与正弦函数族结合计算裂缝参数信息以及用二阶矩自动对溶蚀孔洞进行椭圆拟合并计算孔洞参数信息的方法。为测试和验证该方法的有效性和适应性，将所研究方法应用于某油田多口井的实测电成像数据，初步证实了算法的高精度和有效性。

1 用于电导率图像基质和缝洞电导率异常自动分离的Otsu算法

在这一部分，应用大津法(Otsu)从井壁采集获得的FMI图像中自动分离裂缝和孔洞[23]。Otsu算法的基本思想是指定一个阈值，该阈值可以参考图像灰度图的像素分布柱状图以便将图像分成两部分，且两部分的方差达到最大。

如图1所示，设计了一个图像G，它是Q×R像素大小的图像，

设g(x,y)是分布在(x,y)范围内的图像的灰度函数。通过在灰度图的像素值区间里测试不同的阈值来获得最优的图像分割阈值thresh，该阈值可以让被分割成两部分的方差σ2(thresh)达到最大，该算法的具体实现如图1所示。

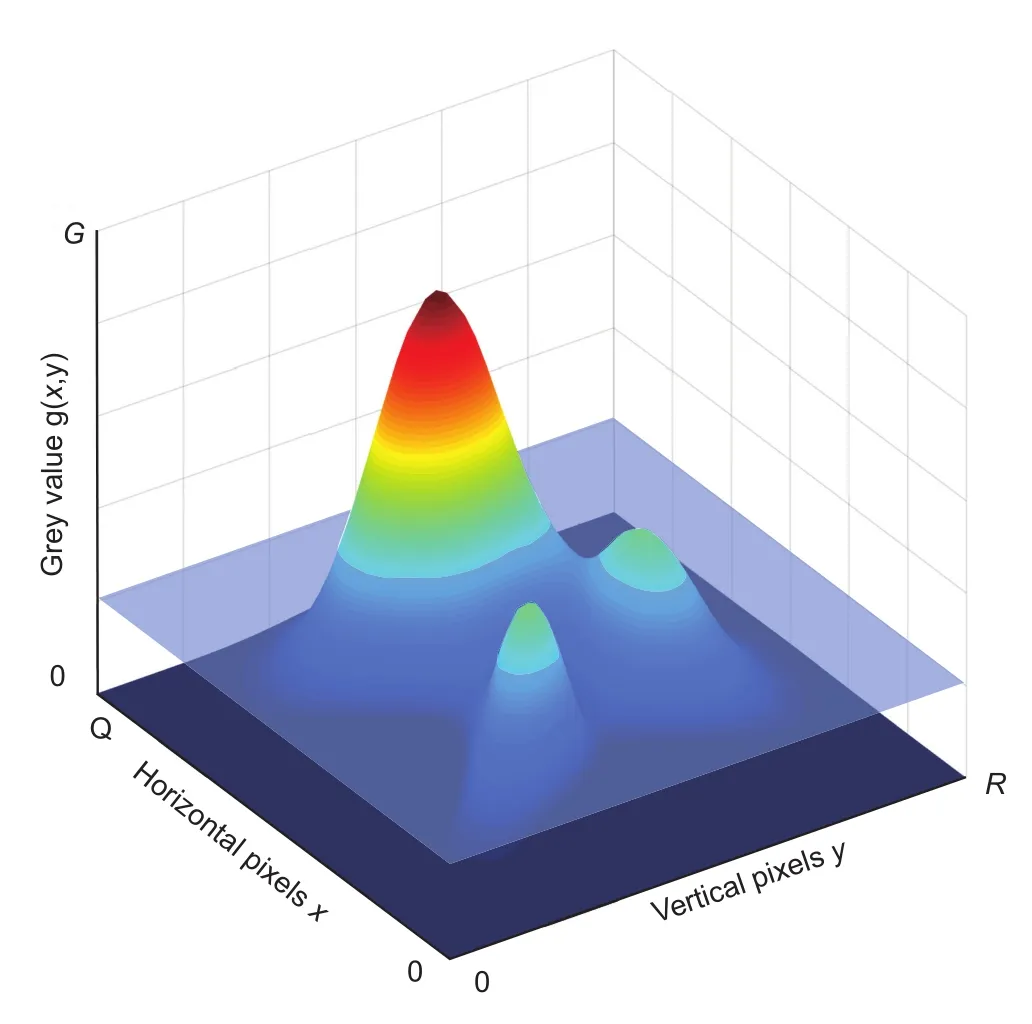
图1 Otsu算法示意图Fig.1 A schematic diagram of Otsu method

对于二维电导率图像来说，可以把阈值thresh作为分割的参照。高于thresh的所有像素点设定为1，该像素点对应于井壁岩石的基质部分，低于thresh的所有像素点设定为0，该像素点对应于井壁岩石的裂缝、溶蚀孔或洞部分。通过这一过程，灰度电导率测井图像矩阵变成了0-1二值矩阵。图2a是原始灰度缝洞成像图，图2b是基于小波变换与快速行进算法插值后的图像[24]；图2c是Otsu分割后的裂缝、溶蚀孔或洞图像。图中可以看出，裂缝、溶蚀孔或洞可以较好地与基质部分实现分离。

2 不完备路径形态学缝洞识别方法

图2所示的电成像测井电导率图像中暗色或黑色斑块或条带显示了可能存在的裂缝或溶蚀孔洞，如何从这些图像中识别和分离出该类电导率异常是电成像测井缝洞储层识别与评价的首要任务。下文首先简单介绍从电导率图像中提取高电导率异常并分离缝洞的方法原理。

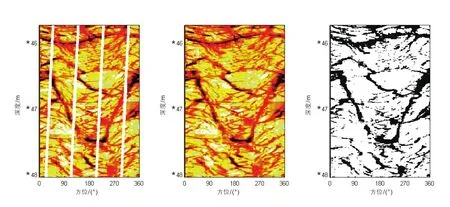
图2 (a)原始灰度缝洞成像图；(b)基于小波变换与快速行进算法插值后的图像；(c)Otsu分割后的缝洞图像Fig.2 (a) Original electric imaging logging image; (b)Electric imaging image interpolated by means of wavelet transform and fast matching method; (c) Fracture-vug image separated by the Otsu method

2.1 基于二值图路径开的裂缝识别

路径形态学与传统的数学形态学开闭运算不同，包含了诸多与路径相关的概念。首先是带方向的临近关系的概念。设E是一个已知节点的集合，代表像素点的位置。使用二元的临近关系“↦”来定义一个在这些节点之上的有向图。具体地，x↦y表示存在一条从x到y的路径。如果x↦y，就称y是x的后继节点，x是y的前驱节点。这个概念在图3中有展示。b1、b2、b3是a的前驱节点，a1、a2、a3是b的后继节点。图3中可以看到，箭头表示的临近关系规定了节点与节点之间的继承方向是从左至右，分别为45°，0°，-45°，而临近关系的角度并不局限于45°的倍数，可以任意选择。在FMI图像中应用该方法时，通过事先定义临近关系，可以把结点间以不同的方向串连起来，提取与实际测井资料相符的图像特征。

图3 邻接关系示意图，b1、b2、b3是a的三个前驱节点，a1、a2、a3是b的三个后继节点Fig.3 Adjacency relation of set a and b, where a is the successor of b1, b2, b3, and b is the predecessor of a1, a2, a3.

如果存在一个空间分布结构恒定不变的二维节点图，当若干节点满足图4所示的临近关系，那么其中会包括多条不同形状的长度为L的路径。由于每个点的前驱结点与后继结点的数量均为3个，以任一结点为起始点的长度为L的路径会有3L-1种情况，因此，路径形态学算法的耗时与L呈指数型上升，同时对内存的要求也会逐步提高。针对这一问题，Talbot等提出了一种新的快速算法[25-28]。假设存在东西方向的二维临近关系节点集合E，X是节点图E中的任意子集。给定函数b：

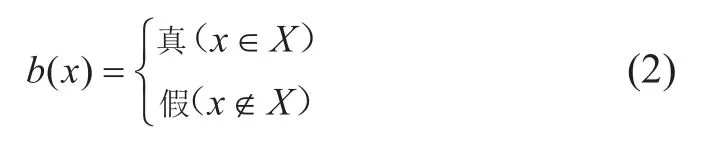
对于二维临近关系节点集合E，在每个像素点p存储两个值：起始点为p且方向为右的最长路径的长度λ+[p](该长度不包含点p自身)，以及起始点为p且方向为左的最长路径的长度λ-[p](该长度不包含点 自身)，其计算公式如下：

其中，p1，p2表示二维节点图中点p的横纵坐标。

当二维临近关系节点图满足图4(a)且b[p]=真时，可以通过对每个符合条件的路径上的节点重复利用式(3)和(4)的关系，分别计算得到节点图中每个像素点p(p1,p2)的向右最长路径节点数λ+[p]、向左最长路径节点数λ-[p]，进而根据式(5)求得包含节点p的最长路径总的节点数λ[p]：

图4 四种邻接关系的组合Fig.4 Four kinds of adjacency relations.

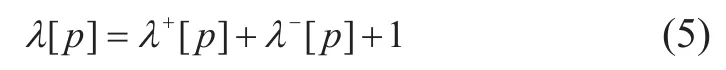
如果点p自身是空缺态，即b(p)=假，那么穿过点p的最长路径不存在，设为λ[p]=0。

图5a～e是一个路径形态学算法在一个8×9的二维临近关系节点矩阵中的示意图。图中黑色节点表示b[p]=真，灰色节点表示b[p]=假，临近关系满足图4a。图5a表示从右侧第一列开始计算经过该列节点的最长路径长度，并逐列向左推进直至最左列(如绿框所示)，所有符合临近关系的黑色节点都用绿色箭头连接起来并在图5c中统计经过各节点的右向最长路径长度λ-[p]。图5b表示从左向右计算图5d中λ+[p]的过程(如蓝框所示)。图5e按式(5)计算路径开的值λ[p]。此时如想获得长度大于L的路径，只需从图5e中找出符合条件的节点，这就是路径开运算追踪裂缝分布的原理。

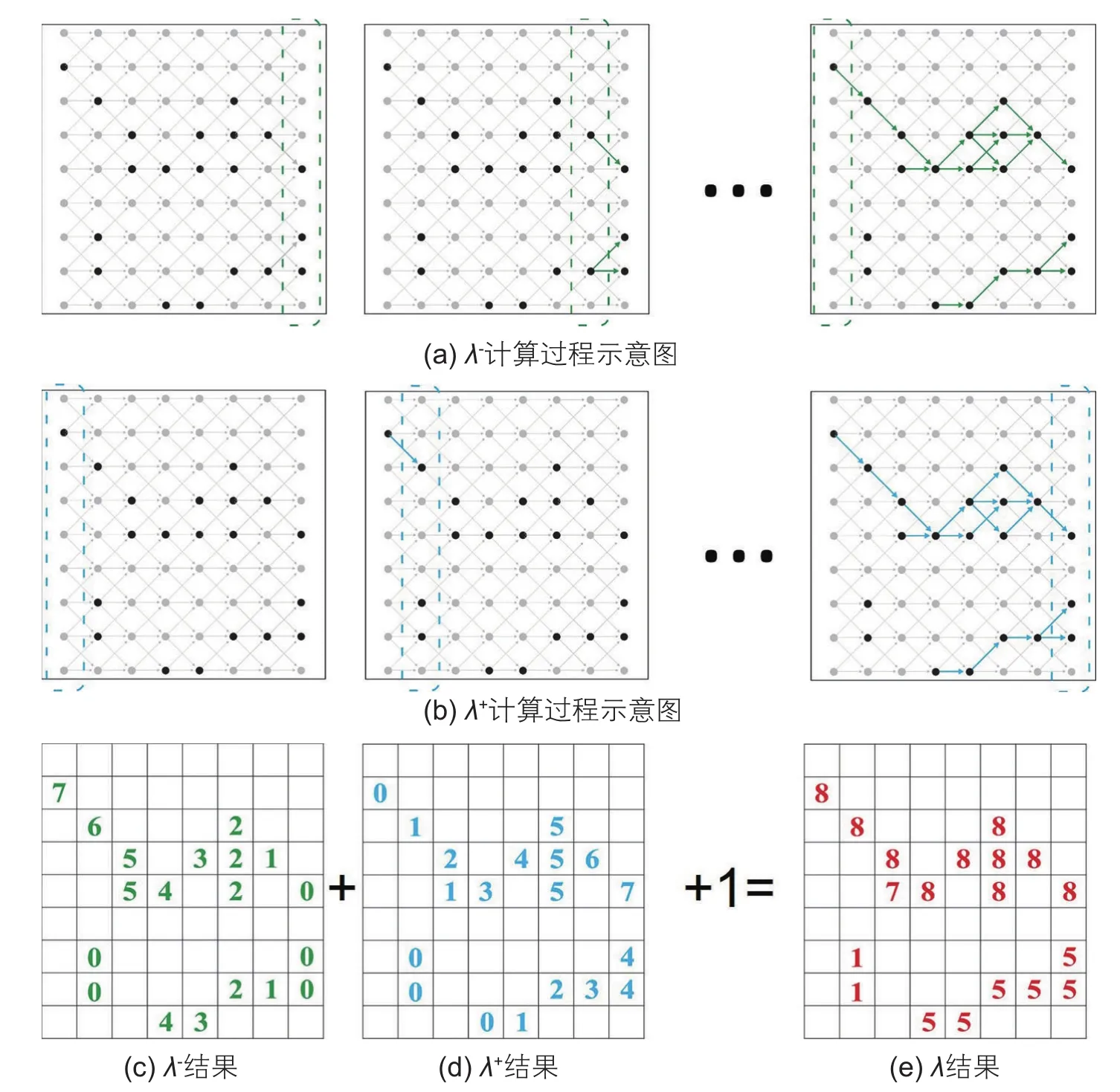
图5 二维临近关系路径开运算示意图Fig.5 The diagram of the path opening algorithm in a 2-D adjacency relations

2.2 基于二维节点图的不完备路径开的裂缝识别运算

在二维节点图中使用长度因子L进行路径开运算时，各节点间的临近关系是逐点相连的，路径中不存在节点缺失的情况，而实际的裂缝常因地层运动、仪器与井壁耦合性不良或含有不规则噪声导致测井图像中某一条裂缝从中间断开，形成多条路径长度较短的小裂缝。因此若只使用长度因子进行裂缝的提取，当L取值较大时，会大大降低对有间断裂缝的提取效果。

针对这一问题，可以从Talbot等改进的不完备路径形态学算法获得借鉴，该算法引入了容忍因子K，当某一条路径上有K个节点丢失时(b[p]=假)，使用路径长度因子L仍可以对间断路径进行有效识别和提取，尤其是对背景包含较多点状噪声的路径提取效果较好。容忍因子的使用示例如图6所示。图6a是包含间断的裂缝，可以看到裂缝右侧有2个节点丢失；图6b是L=6时的完备路径开的提取结果，右侧裂缝的路径长度为5，不符合路径长度条件，无法有效提取；图6c是L=6，K=3时的不完备路径开的提取结果，由于容忍因子K的存在，丢失的2个节点没有影响到裂缝右侧部分的提取。由此可见路径长度因子L与容忍因子K同时使用可以提高间断裂缝的识别效果。

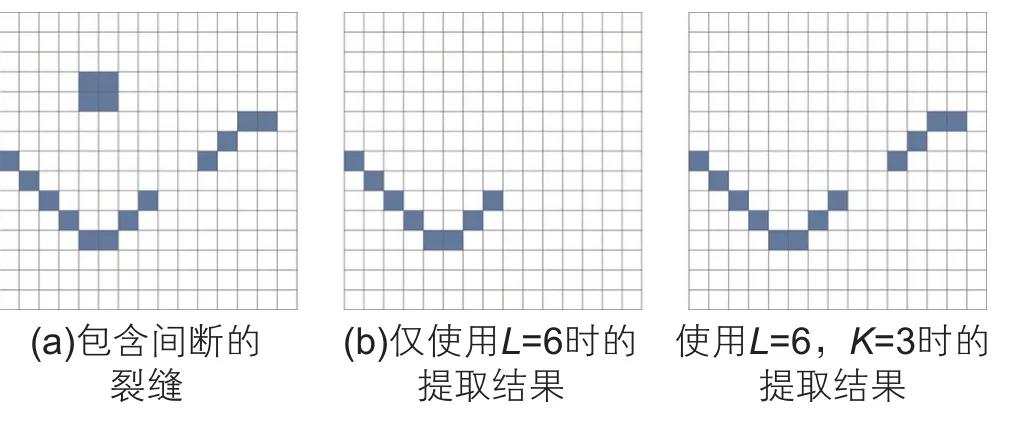
图6 基于不完备路径的裂缝提取示意图Fig.6 The diagram of the fracture extraction based on the incomplete path opening method

用λ[p,k]表示节点p在缺失路径长度为k即路径容忍因子K=k情况下通过该点的最长路径长度。需要注意的是，缺失路径长度k表示多个连续节点的缺失，而不是某一条路径中多处缺失节点的个数之和，如图6c中缺失的2个节点必须连在一起。类似完备路径开运算的过程，不完备路径开同样是先左向逐列计算λ-[p,k1]，再右向逐列计算λ+[p,k2]。当b[p]=真时，k1+k2=k；当b[p]=假时，k1+k2+1=k。如果经过该节点的路径在这里存在长度为k的间断，需要利用上一个间断长度为k-1的符合临近关系的最长路径来辅助计算，详细公式在下面给出。

若b[p]=假：

若b[p]=真：

根据公式(6)～(10)对每个节点p(p1,p2)递归计算λ-[p,k]和λ+[p,k]。

2.3 不完备路径形态学对模拟含噪声电成像数据的处理分析

为了考查不完备路径形态学与Otsu算法对模拟含噪声电成像数据的适应能力和处理效果，设计了含噪且溶蚀孔洞与多条相交裂缝共生的缝洞储层电成像响应模型。下文将测试不同参数对去噪和缝洞分离的效果。

如图7a所示，设计两条相交裂缝和两个不同尺度溶蚀孔洞的组合模型，大小是552×314像素。图中可以看到两个正弦裂缝均被断成了多个部分，还有两个线段表示直线型裂缝或者雁阵型诱导缝，两个椭圆表示不同直径和纵横比的孔洞，并给图像加上方差为0.005的二维高斯噪声。图7b针对图7a进行了彩色图转换成灰度图的操作，图7c利用了Otsu算法对图7b进行了二值化分割，其中白色部分像素值是1，黑色部分是0。可以看到图像的背景都被去掉了，仅剩裂缝、孔洞和噪声，正弦型裂缝中存在间断的最长距离小于15个像素长度。

图8是利用不同的不完备路径形态学参数组合对图7c两条裂缝图像提取的效果。其中，图8a是L=90，K=0时的提取效果，即完备路径形态学下L=90的效果。此时因为背景噪点的路径长度都小于90，所以噪点被去除了，同时被去除的还有一条直线型小裂缝和两个椭圆状孔洞。图8b是L=90，K=15时的提取效果，此时图7c中一个较大的孔洞较长的一部分再次出现，另一个直线型小裂缝亦然。图8c是L=150，K=0时的提取效果。此时小的直线裂缝和孔洞都被去掉了，但是因为此时是完备路径形态学提取，所以两条正弦型裂缝中间断型存在的部分就被略去了，这无法满足要求。

图7 两条正弦型裂缝示意图Fig.7 A schematic diagram of two sinusoidal curves

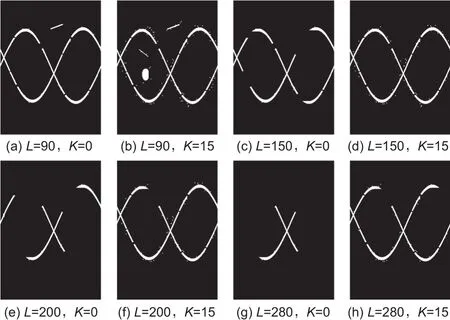
图8 不完备路径形态学算法不同参数组合的提取效果Fig.8 Different extraction results of combinations of parameters by incomplete path opening operation

由于正弦型裂缝中存在间断的最长距离小于15个像素长度，所以选择容忍阈值15。图8d是L=150，K=15时的提取效果。在增加了容忍阈值的设置后，两条正弦型裂缝被完整提取出来，对比图8c，可以看到不完备路径算法的优势。

继续增大L，图8e是L=200，K=0时的提取效果，此时两条正弦型裂缝中的大部分被略去了。图8f是L=200，K=15时的提取效果，增加容忍阈值的设置，正弦型裂缝中仍然有一小部分缺失，这表明L设置过大。图8g～h是L=280时的提取效果，作为L设置过大的极端情况，无论K值是否是0，裂缝都无法被完整提取。综上，可以看出使用不完备路径形态学在参数组合L=150，K=15的时候，两条正弦型裂缝的提取效果最好。

3 密度聚类算法以及正弦函数族算法对相交裂缝的分离

在实际的测井资料中多是如图7a那样两条甚至多条交织在一起的正弦曲线，为了把这两条正弦曲线分开，本文在使用不完备路径形态学算法的基础上结合密度聚类算法以及正弦函数族匹配的算法来完成。

3.1 密度聚类算法对多条相交裂缝的提取

图9a是对图8c使用L=150，K=15的路径形态学算子提取的结果，之后进行去噪，采用长和宽均是4的disk型结构元素对图像进行开运算操作，即对原图像先腐蚀后膨胀，图9b是去噪后的结果，图中可以看到白色噪点被去除，而两条正弦曲线几乎没有受到破坏，去噪效果良好。下边分析对图9b进行两个方向的路径形态学分离。

仍然使用容忍阈值L=150，K=15的不完备路径形态学算子对图9b进行提取，但不再是如图4所示的四个方向的提取，而是选取了其中的两个方向，以方便后续讨论。图10a是算子“下-右下-右”的示意图，图10b是用该算子提取的结果；图10c是算子“上-右上-右”的示意图，图10d是用该算子提取的结果。可以看到图10b和图10d分别提取出了带有间断的裂缝的一部分。虽然在每一条裂缝上还留着与之接近垂直方向的裂缝的“刺”，但它对下一步的分离效果几乎没有影响。为了完成缠绕裂缝的分离，选用聚类方法来实现。

图9 开运算去噪效果图Fig.9 A denoising result by open mathematical morphology method

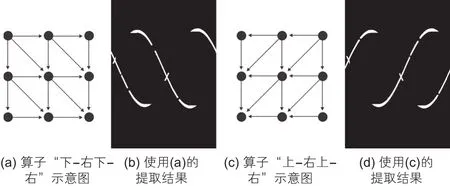
图10 使用两个不同方向的不完备路径形态参数组合提取的结果Fig.10 Results by using two different directions of incomplete path opening parameter combinations

基于聚类的算法是机器学习中涉及对数据进行分组的一种算法，通过分析给定数据集在不同域的分布规律，可以把数据分成多组，同一组内的数据具有相同或类似的特征，而不同组之间的数据特征不一致。常见的聚类算法有K-means聚类、Mean-Shift聚类、基于密度的带噪声的空间聚类(DBSCAN)等[29]。本文使用的是DBSCAN算法，它包含两个重要参数：ε(邻域距离参数)和minPts(邻域最少样本点参数)，该算法用这两个参数来寻找数据集内各点在某一坐标域内具有较高密度的数据点的组合，并把组合划归成不同的簇，具体运算关系可以用下列式子表示：

样本数据集D= {x1,x2,...,xm}。

定义以下概念：

ε-邻接距离

设xj∈D，其ε-邻接距离指的是在数据集D中与点xj不远于ε的数据，用Nε(xj) = {xi∈D|dist(xi,xj)≤ε}表示；

核心有效数据点

若xj的邻域具有不少于minPts个数据点，满足Nε(xj)≥minPts的条件，那么xj被认为是核心有效数据点，minPts数包含了xj自身。

直接触及关系

对xi与xj，若xi是核心有效数据点且xj与xi的距离不大于ε-邻接距离，则称xj由xi构成直接触及关系；

触及关系

对xi与xj，若存在xk使得xi与xj均与xk构成直接触及关系，则称xj由xi构成触及关系；

图11是一个简单的算法示意图，图中minPts=3。图中各个圆环表示ε-邻接距离，核心有效数据点是x1，可以看到x2、x4与x1均构成直接触及关系，而x3与x1构成触及关系，因此x3与x4也构成触及关系。

图11 DBSCAN算法示意图Fig.11 A schematic diagram of DBSCAN algorithm.

从上述定义出发，基于密度的带噪声的空间聚类的应用算法给出了“簇”的定义，即一定区域内最大数目的多个互相构成触及关系的数据点连接到一起的集合。若x为核心有效数据点，那么找到所有与之有触及关系的集合为X={x'∈D|x'由x密度可达}，X满足簇的连接性与最大性的性质。

按(ε，minPts)参数重复上面的过程，直到数据集内所有点都被该算法扫描完毕。

对于有间断的两条正弦曲线，选用不同的聚类参数组合会得到不同的结果。图12是在ε=3，minPts=3的情况下获得的结果。

图12b和e分别是用两条带有间隔的正弦曲线通过不完备路径形态学在图12a和图12d方向的提取结果。对图12b和e进行密度聚类，参数设定为ε=3，minPts=3，这时如果3个及以上的像素点每两个像素点周围不大于3，它们都会被划入同一个聚类簇，得到的结果如图12c和f所示。由于间隔的存在，同一条正弦曲线中间隔都大于3个像素距离，可以看到图12c和f均被DBSCAN算法自动分成了7种颜色对应的7部分，本应该通过密度聚类算法分到一起的正弦曲线段因为间断的存在而被分割成多个部分，这没有达到做密度聚类的初衷。

图12 两条带有间隔的正弦曲线使用不完备路径形态学提取后密度聚类的结果。(a)不完备路径形态算子的提取方向一；(b)使用a获得的提取结果；(c)对图b的密度聚类结果；(d)不完备路径形态算子的提取方向二；(e)使用d获得的提取结果；(f)对图e的密度聚类结果Fig.12 Results by DBSCAN after using incomplete operation on two sinusoidal curves with several intervals.(a)First direction of incomplete path opening operator; (b)The result by using operator a; (c) The result of DBSCAN on b; (d)Second direction of incomplete path opening operator; (e)The result by using operator d; (f) The result of DBSCAN on e

尝试使用另一组聚类参数组合。图13是在如果ε=30，minPts=3的情况下获得的结果。

图13b和e分别是用两条带有间隔的正弦曲线通过不完备路径形态学算法在图13a和d方向上的提取结果。对图13b和e进行密度聚类，参数设定为ε=30，minPts=3，这时如果3个及以上的像素点每两个像素点周围不大于30，它们都会被划入同一个聚类簇，得到的结果如图13c和f所示。由于同一条正弦曲线中间隔都小于30个像素距离，所以可以看到图13c和f被分成了3种颜色对应的3部分，原来属于一条正弦曲线的部分被归为一类，因此密度聚类的结果是正确的。

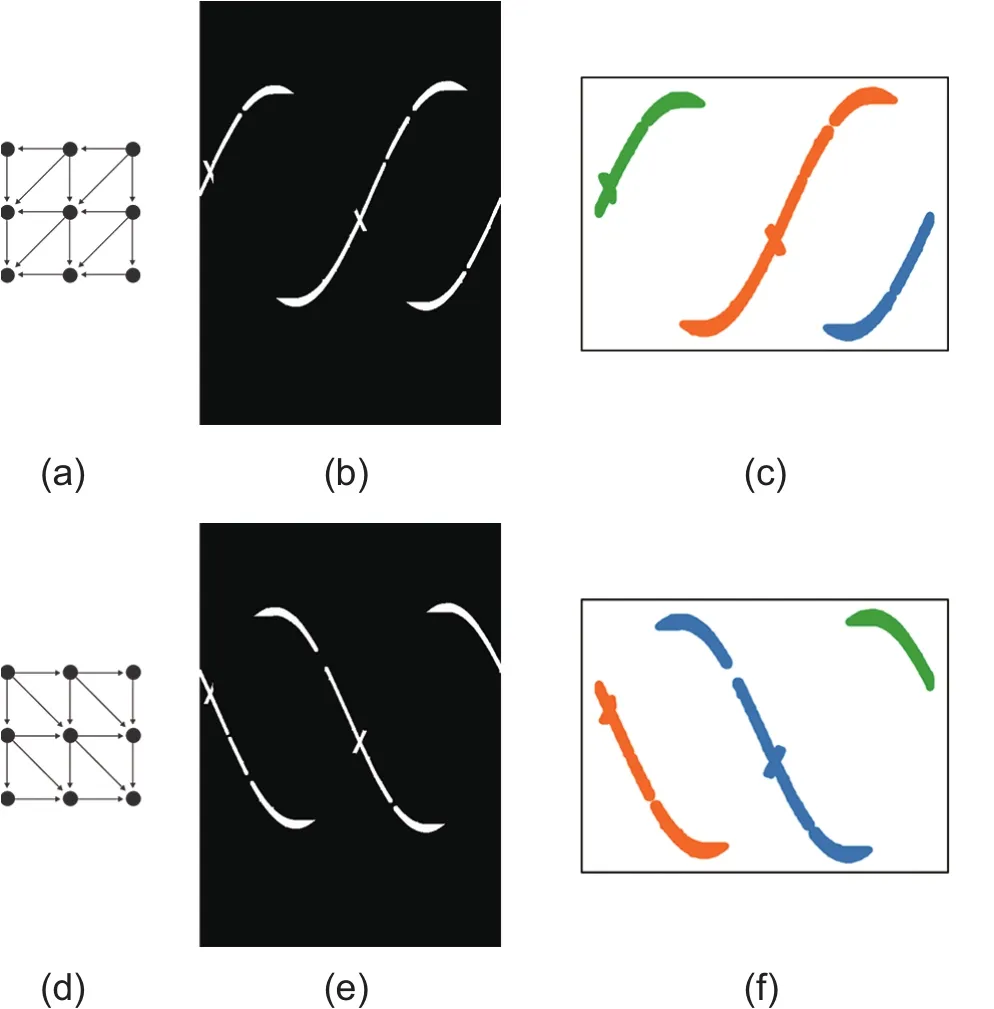
图13 两条带有间隔的正弦曲线使用不完备路径形态学提取后密度聚类的结果(a)不完备路径形态算子的提取方向一；(b)使用a获得的提取结果；(c)对图b的密度聚类结果；(d)不完备路径形态算子的提取方向二；(e) 使用d获得的提取结果；(f)对图e的密度聚类结果Fig.13 Results by DBSCAN after using incomplete operation on two sinusoidal curves with several intervals (a)First direction of incomplete path opening operator; (b)The result by using operator a; (c) The result of DBSCAN on b;(d) Second direction of incomplete path opening operator; (e)The result by using operator d; (f) The result of DBSCAN on e

3.2 基于正弦函数族的裂缝参数提取算法

由电导率图像提取和分离裂缝与溶蚀孔洞后，下一个关键任务是裂缝和溶蚀孔洞参数的定量评价。对于规则裂缝与井孔相交在电导率图像上呈一条有初始相位角的正弦曲线，非规则裂缝则呈现变形的曲线。溶蚀孔洞则在电导率图像上大多呈椭圆形，也有不规则形状。因此，根据分离的裂缝与溶蚀孔洞分别拟合，求取裂缝开度、方位倾角以及溶蚀孔洞的长短轴、纵横比和面孔率等参数。下面针对不同缝洞的组合形状，分析相应的拟合方法。

Hough变换可以针对电成像测井图像中的正弦型裂缝进行提取，方法是把图像变换到参数域后计算出裂缝的振幅和相位参数[30]。在转换的过程中，如果图像中的裂缝曲线归属于同一个正弦曲线，那么在参数域会叠加在一点上。在测井解释中，Hough变换参数域是作为一个投票器来对图像中的各点变换后的信息进行投票。在投票结束后，参数域中较高的那一点会分别显示出图像中对应曲线的振幅和相位。

Hough变换的优势是能快速提取微电导率测井成像中的裂缝信息，但它也有缺点。第一，噪音的存在影响了正弦曲线的提取；第二，对高角度裂缝拟合容易出现较大误差。

从前面的描述中，知道电导率测井成像中的裂缝信息可以用正弦函数来表示，因此可以尝试使用模式识别的方式来提取裂缝。在本文中，构建了一个正弦函数族来进行实际图像的裂缝提取。所有接近正弦型的裂缝理论上都可以用正弦函数族来进行拟合。拟合的原理为2-D相关算法[11]：

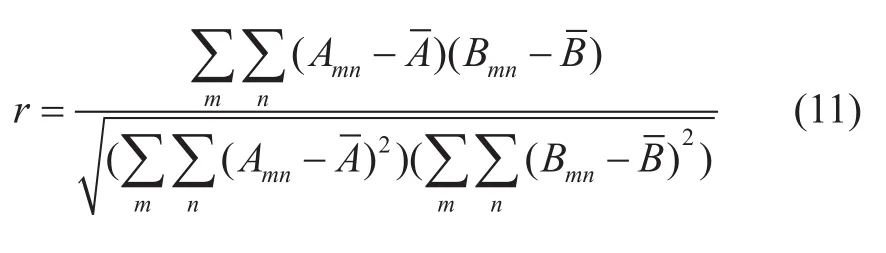
其中，r表示2-D相关系数，A表示实际的裂缝成像数据，B是正弦函数族。和分别表示A和B的平均值。

为了对比Hough变换和正弦函数族拟合提取裂缝的优势，这里分别考虑低角度和高角度的裂缝(水平裂缝和竖直裂缝也可以按照类似的方法处理)。正弦函数族的基本参数设置如下：倾角区间设为-75o～75o，相位区间设为0o～360o。在井径已知的情况下，正弦函数的振幅可以通过倾角计算出来，深度可以通过实际的FMI成像资料获得。基于这样的设定，正弦函数族就可以被建立起来。在实际的计算过程中，倾角区间和相位区间的步长应该根据测井数据的大小和粗细等情况斟酌，因为当单位步长太小时，正弦函数族的计算代价会非常高；当单位步长太大时，最后的匹配计算精度会变差，因此应寻找一个计算代价与精度的平衡点。

图14a展示了三条残缝，本节试图用不同的方法来重建原始的正弦曲线。从图14b～c重建结果和图14e轮盘的对比结果可以看到正弦函数族匹配的结果精度更高，更接近残缝原始的振幅，而使用Hough变换重建的正弦曲线振幅超过了原始模型的振幅，同时从图14d看到Hough变换域也并不是全部收敛到某一个“亮点”上。因此当原始残缝的信息不够多时，使用Hough变换提取的结果精度较低。

图15是使用正弦函数族对图13b和13e聚类后的一共6部分分别进行重建恢复的结果。文中使用了32GB的内存RAM来进行重建工作，匹配精度较高。可以看到各部分的重建裂缝与模型最初的正弦型很接近，但有一些振幅出现了偏差，这是由于残缝提供的信息太少导致的。该匹配过程可以在更高内存的工作站上使用相位、振幅和深度间隔步长更小的正弦函数族来进行匹配，精度更高，但会花费更多的时间和内存计算成本。

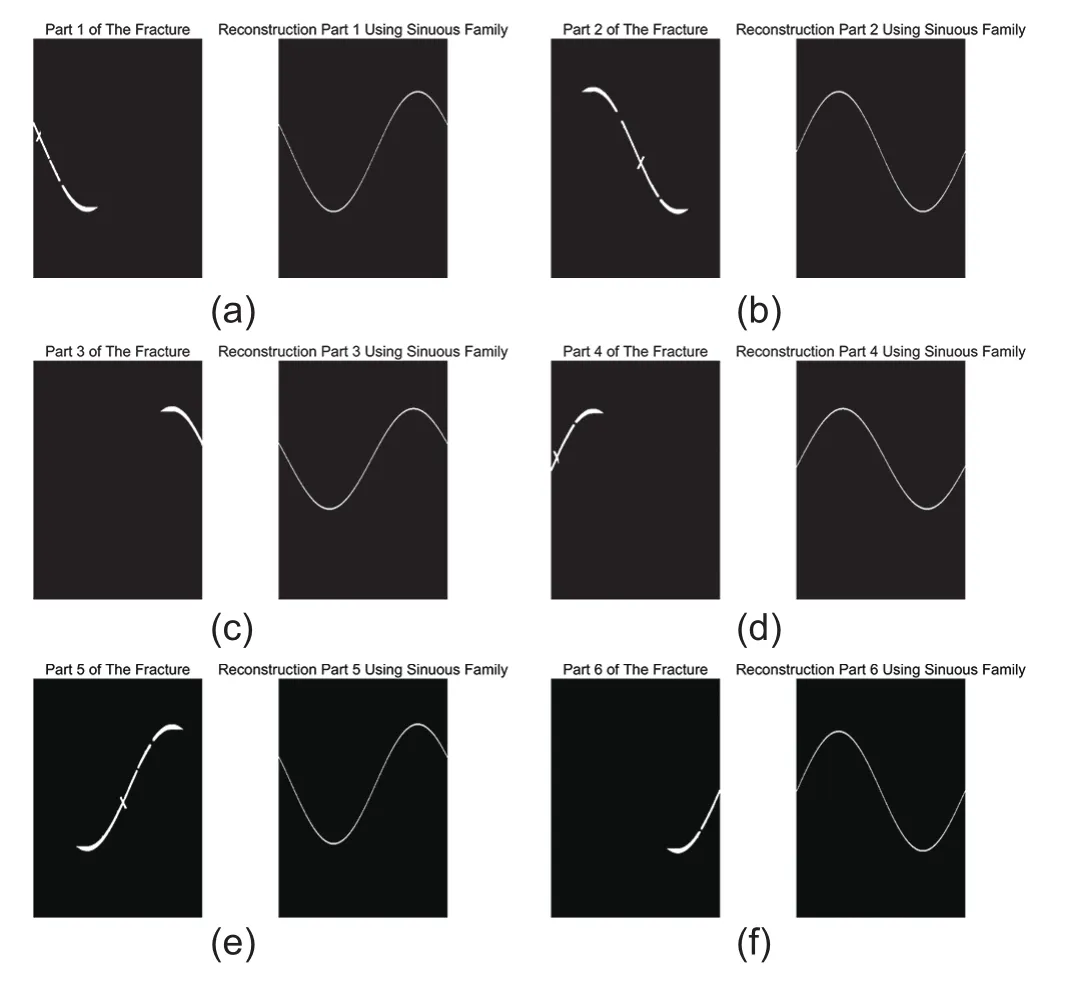
图15 使用正弦函数族对图13b和图13e聚类后的各部分分别进行重建恢复的结果Fig.15 The reconstruction results of every part after DBSCAN in Fig.13b and Fig.13e

接下来对恢复重建的正弦函数进行归类，假定恢复后的两个正弦函数的相位差及深度差满足：

(1)φi-φj＜π/4,1 ≤i≤ 6 ,1 ≤j≤ 6且i≠j；

(2)Depthi-Depthj＜ 0.2,1 ≤i≤ 6 ,1 ≤j≤6且i≠j。

即可以认定这两个正弦函数属于同一条裂缝，那么它们对应的原来的残缝也隶属于同一条裂缝。这是因为在实际地层中，深度间隔小于0.2 m的任意两条残缝的相位如果小于π/4，那通常是由于地层挤压或拉伸造成同一个地层发生了错位导致的。基于该思想，把图15a～f中所有隶属于一条裂缝的残缝叠加到一起，可以得到如图16的结果，图中可以看到，两条正弦曲线被较好地分离开来。

图16 (a)使用形态学算法去噪后的电导率测井图像；(b)从a中分离出来的第一条裂缝；(c)从a中分离出来的第二条裂缝Fig.16 (a)The electric imaging logging image after denoising by mathematical morphology; (b)The first separated fracture from a; (c) The second separated fracture from a

4 基于二阶中心矩的溶蚀孔洞拟合与参数提取算法

上一节对碳酸盐岩缝洞型储层的电导率图像利用不完备路径形态学和正弦函数族算法实现了缠绕裂缝的分离，但仅分离了裂缝，为了后续测井处理时计算渗透率、饱和度，同深度段的溶蚀孔洞信息需要被进一步计算，例如孔隙纵横比、准确的深度分布等。本节将围绕该主题，使用基于二阶中心矩椭圆的孔洞拟合和参数提取算法得到溶蚀孔洞在空间上的分布及特征。本节先对二阶矩拟合算法进行公式推导，然后展示模型数据的计算结果。

4.1 二阶中心矩溶蚀孔洞椭圆拟合算法

传统文献关于椭圆拟合的思路分为两个路线：最小平方拟合[31]和聚类算法[32]。与传统的基于散点图的椭圆拟合不同，孔洞在图像上是一块区域，不是多个边缘散落点的组合，提取更为复杂，涉及的参数也更多，且孔洞结构的复杂性又增大了其参数提取的难度。为了便于实际应用，文中用不同尺度与偏心率的二阶矩椭圆形函数来拟合孔洞。

一般来说，可以对一个实际物体在任意维度上通过定义一个矩来获取它的有效信息。对实际物体可以认为它有一个总的质心，这对应的是一阶矩。在图像中，二阶矩可以被用来决定与该物体对应的椭圆，从中可以找出长轴和短轴的长度及方向。

图像的矩通过图像中像素的密集程度来定义。在一个像素密度为I(i,j)的灰度图中，简单的二维(p+q)矩Mp,q按如下给出：

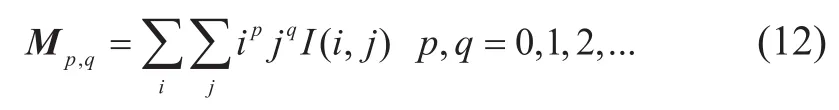
在下面的讨论中，灰度图像矩的计算对图像的局部对比度有较强依赖，因此处理起来更加困难。所以在进行计算前，先把图像变成二值图，即图像中物体的像素值变成1，而背景值变成0。对于一个二值图，(p,q)矩Mp,q可以被定义如下：

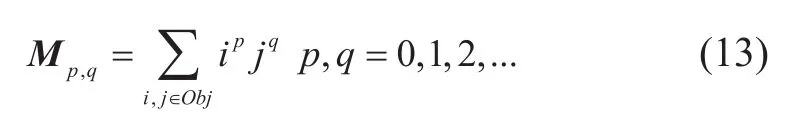
零阶矩M0,0给出了物体的总像素点数，可以理解为其面积。一阶矩M1,0和M0,1可以理解成该物体分别在水平和垂直方向的重心：

从这里开始，算法就变得复杂起来，从二阶矩M2,0，M1,0和M0,2中提取等效椭圆的参数不是最简便的方法，因为必须使用二阶中心矩，这与计算物体的刚度二阶矩不同。它们的表达式如下：

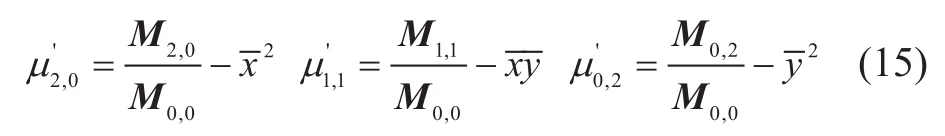
经过上述计算，二值图像中物体的协方差矩阵变成

该协方差矩阵的特征向量对应了物体等效椭圆的长轴和短轴方向。如图17所示，等效椭圆度的长轴与x轴的夹角θ、长轴长度l和短轴长度w的最终形式为：

图17 拟合后的椭圆示意图Fig.17 The schematic diagram of ellipse approximation

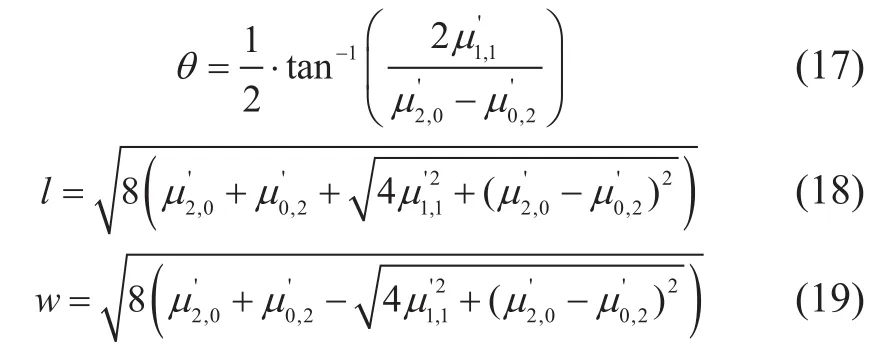
确定椭圆中心位置后，还需统计目标区椭圆的面积，以便定量计算面孔率。椭圆面积计算公式为：

椭圆对应的三维空间的椭球体积计算公式为：

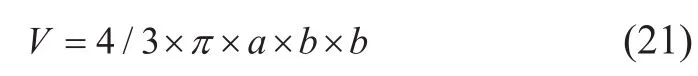
其中，a、b分别对应了椭圆的长、短轴长度的一半。

椭圆的纵横比计算公式为：

4.2 模拟数据测试

为了测试前文椭圆拟合算法的有效性，本文选取了散列的硬币图像进行二阶矩椭圆拟合，并给出了椭圆的中心点，效果如图18所示，可以看到二值图中每枚硬币使用二阶中心矩椭圆拟合后找到了对应的椭圆及中心。

图18 (a)原始硬币图像；(b)用二阶中心矩拟合各硬币的椭圆Fig.18 (a)The original images of coins; (b)Enclosing ellipses of these coins based on the second-order centric moments method

5 测井数据计算与缝洞储层评价应用

5.1 不完备路径形态学和正弦函数族算法在提取裂缝参数过程中的应用

图19是对正弦函数族方法与改进的Hough变换方法在实际电成像测井资料中的效果进行比较。

图19a中包含三条断裂的裂缝，其中上下两条缝发育较好，但中间的裂缝被岩层的基质切断。图19b是使用不完备路径形态学算子L=40，K=5对二值化后的图像提取的结果，基质、孔洞等被剔除，只剩下三条较大的裂缝。图19c是用改进的Hough变换重建的裂缝，图中上下两条裂缝被较好重建出来，但中间的裂缝由于原来电导率图像中只有部分信息，因此用Hough变换重建出现了错误。图19d是用正弦函数族进行模式识别的结果，可以看到三条裂缝都获得了较好的恢复效果，中间残缝的重建结果与原电导率图像吻合。图19e为实际电成像测井资料用两种方法得到的参数的罗盘图，可以清晰看到正弦函数族得到的参数和模型参数基本吻合，而Hough变换则存在较大误差。因此可以断定，当初始模型有效信息较少，裂缝不完整的情况下，正弦函数族提取的裂缝参数比Hough变换得到的结果更准确。

图19 (a)原始的电导率测井图像；(b)使用不完备路径形态学算子L=40，K=5提取的空白条带插值后的结果；(c)使用Hough变换重建的裂缝；(d)使用正弦函数族重建的裂缝；(e)Hough变换和正弦函数族重建的结果对比Fig.19 (a) The original electric imaging logging data; (b) The extraction by incomplete path opening operation with L=40 and K=5 of the blank area interpolated data; (c) The reconstruction fractures using Hough transform; (d) The reconstruction fractures using the cluster of sinusoid; (e) The comparison of Hough transform and the cluster of sinusoid results

接下来使用正弦函数族与不完备路径形态学方法结合，对实际的微电导率成像中存在缠绕现象的裂缝进行分离。

首先使用不完备路径形态学路径算子和容忍算子来进行裂缝的提取。

图20a是原图，大小是735×441，图中可以看到有两条相交裂缝，在裂缝周围分布着各种溶蚀孔洞。图20b是原图先使用Otsu算法进行二值化之后用开运算处理的结果。图20c是L=30K=5的提取效果，可以看出因为路径长度因子较小，且容忍因子K非0，所以一部分溶蚀孔洞仍然得以保留。图20d是L=56，K=0的提取效果，可以看出路径长度因子变大使一部分溶蚀孔洞被剔除，但构成裂缝的长度较短的部分由于容忍因子为0，没有被提取出来。图20e是L=56，K=5时的提取效果，可以看出连通图20d遗漏部分的两条裂缝被较好提取出来。图20f是L=56，K=15时的提取效果，由于容忍因子K过大，导致裂缝周边的孔洞信息重新出现。综上，提取目标裂缝最好的参数是图20c中的L=56，K=5。

图20 (a)原始电阻率测井图像；(b)使用Otsu算法二值化后的图像；(c)L=30 K=5的不完备路径形态学提取结果；(d)L=56 K=0的不完备路径形态学提取结果；(e)L=56 K=5的不完备路径形态学提取结果；(f)L=56 K=15的不完备路径形态学提取结果Fig.20 (a) The original electric imaging logging image; (b)The binary image after using Otsu method; (c) The extraction result by incomplete path opening operation with L=30 and K=5; (d) The extraction result by incomplete path opening operation with L=56 and K=0; (e) The extraction result by incomplete path opening operation with L=56 and K=5; (f)The extraction result by incomplete path opening operation with L=56 and K=15

下面分别使用“下-右下-右”方向的路径形态学算子和“上-右上-右”方向的路径形态学算子对图20c采用L=56，K=5的参数进行提取，得到如图21(b)和21(d)的结果，然后对这两图使用ε=30，minPts=3的密度聚类参数组合，可以获得图21c和21e的聚类分组，图中可以看到，对用两个方向的路径形态学算子提取的数据分别进行聚类后，数据被分成了4部分，每部分用不同的颜色表示，其中两图右下角的部分是无效数据。

对图21c和21e有效数据使用正弦函数族进行提取和拟合。每部分对应的正弦曲线如图22所示，且每部分对应的正弦曲线的参数列在表1中。

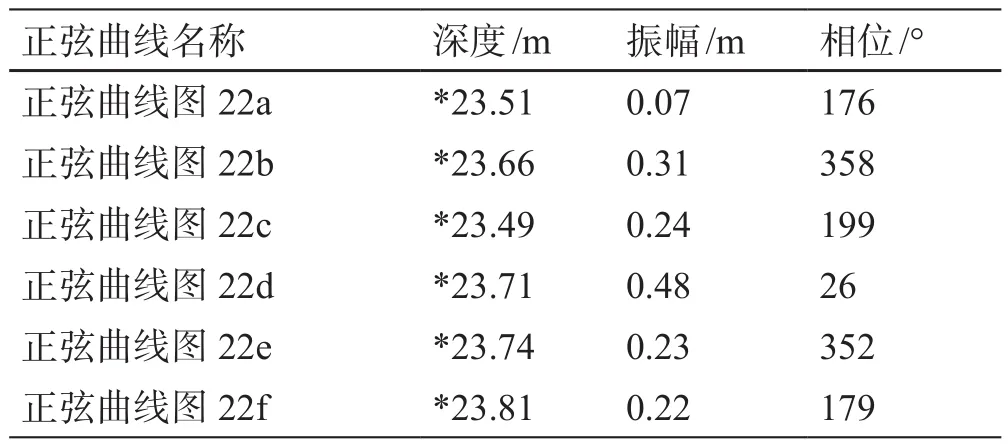
表1 6条拟合得到的正弦曲线的参数Table 1 The parameters of 6 sine curves.

图21 两条裂缝使用不完备路径形态学提取后密度聚类的结果 (a)不完备路径形态算子的提取方向一；(b)使用a获得的提取结果；(c)图b的密度聚类结果；(d)不完备路径形态算子的提取方向二；(e) 使用d获得的提取结果；(f)图e的密度聚类结果Fig; 21 Results by DBSCAN after using incomplete operation on two fractures (a)First direction of incomplete path opening operator; (b)The result by using operator a;(c) The result of DBSCAN on b; (d) Second direction of incomplete path opening operator; (e)The result by using operator d; (f) The result of DBSCAN on e

图22 使用正弦函数族对图21b和图21e聚类后的各部分分别进行重建恢复的结果Fig.22 The reconstruction results of every part after DBSCAN in Fig.21b and Fig.21e

上文中在对恢复重建的正弦函数进行归类时，假定两个正弦函数的相位差和深度差满足一定条件即可以认定这两个正弦函数属于同一条裂缝，那么它们对应的原来的残缝也隶属于同一条裂缝。基于该假设，把六部分残缝进行叠加，获得图23的结果。图中可以看到，两条裂缝被较好地分离开来，且两条裂缝的深度、振幅及相位如表2所示。

表2 两条分离后的裂缝参数Table 2 The parameters of 20 separated fractures.

图23 (a)使用不完备路径形态学提取结果；(b)从a中分离出来的第一条裂缝；(c)从a中分离出来的第二条裂缝Fig.23 (a) The extraction result by incomplete path opening operation; (b) The first separated fracture from a; (c) The second separated fracture from a

5.2 二阶矩椭圆拟合算法在提取裂缝参数过程中的应用

对上节中图21a的微电导率测井图像，使用不完备路径形态学、密度聚类和正弦函数族算法分离出裂缝后，对剩余的孔洞部分使用二阶矩椭圆拟合算法，效果分别如图24所示。

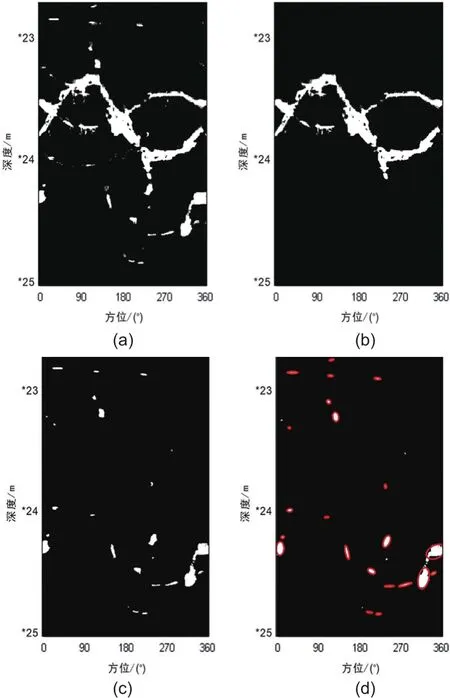
图24 (a)对图19a使用Otsu算法二值化后的图像；(b)从a中分离出来的裂缝；(c)从a中分离出来的孔洞；(d)孔洞基于二阶矩椭圆拟合的结果Fig.24 (a) The binary image to Fig.19 after using Otsu method; (b) Fracture separated from a; (c) Vugs separated from a; (d) The equivalent ellipses of the vugs based on the second-order moments method

对图24中的缝洞参数进行纵横比和面积(像素意义)统计，得到的结果显示在表3中。

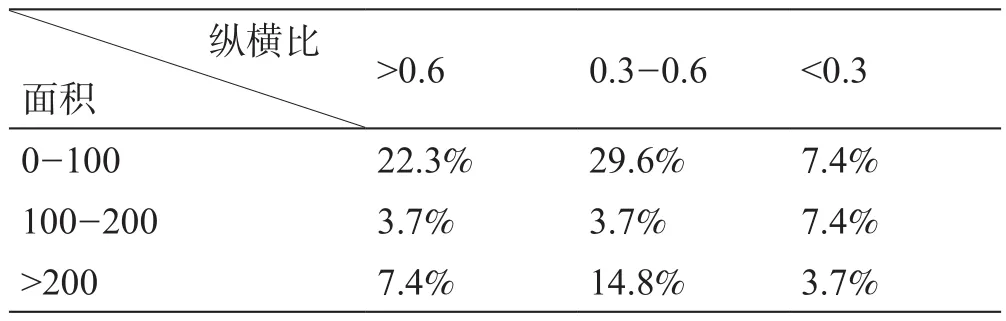
表3 图23孔洞参数统计Table 3 The parameter statistics of vugs in Fig.23

6 结论

本文提出了一种基于不完备路径形态学、正弦函数族和二阶矩椭圆拟合算法由电成像测井电导率图像自动提取和分离裂缝和溶蚀孔洞的方法，通过缝洞模型的模拟数据和实测数据初步验证了方法的有效性，并得到了如下认识：

(1) 路径形态学算法应用于电成像测井电导率图像的去噪、缝洞边缘点检测与分离，可有效地提取裂缝和溶蚀孔洞的信息，实现缝洞自动识别、分离和定量表征。

(2) 文中研究的不完备路径形态学处理算法完全由数据驱动，算法自身具有去噪能力，可以通过扫描路径算子长度和容忍度参数，构造适合处理数据体噪声特点的路径算子，从而可直接对有噪声的成像测井资料进行处理，检测缝洞发育带；对孔洞区域进行二阶矩椭圆拟合的算法可以获得孔洞在像素意义下的面积和纵横比，可以为后续估计对应深度段的孔洞的孔隙度和连通性、渗透率提供支撑，且有助于估计目的层段的含油储量。

(3) 文中算法在成像测井资料处理中的应用仍处于探索阶段，例如，不同形态和尺度的缝洞，在边缘检测时要用不同的路径算子尺度和容忍度。因此，如何在成像测井资料处理中根据地质特征自适应确定合理的算子长度与容忍度参数，仍是一个需要深入研究的课题。