五元联系数的效应全偏联系及其在水问题趋势分析中的应用

金菊良，许继荣，陈梦璐*，张浩宇，宁少尉，陈鹏飞

▪区域农业水管理▪

五元联系数的效应全偏联系及其在水问题趋势分析中的应用

金菊良1,2，许继荣1,2，陈梦璐1,2*，张浩宇1,2，宁少尉1,2，陈鹏飞1,2

（1.合肥工业大学 土木与水利工程学院，合肥 230009；2.合肥工业大学 水资源与环境系统工程研究所，合肥 230009）

【】阐明五元效应全偏联系数的定义，确定其表达公式，刻画其物理内涵，明确其用于解决相关水问题的实际应用价值。采用类比分析的方法，通过分析三元效应全偏联系数的已有成果，确定五元效应全偏联系数的计算公式，借助偏联系数趋势曲线的面积进一步解释五元效应全偏联系数的物理内涵，并将其运用于实际的水问题分析中。①五元效应全偏联系数与五元四阶全偏联系数用于四川省水资源承载力动态评价的结果具有一致性，同时五元效应全偏联系数具有评价对象发展趋势更加清晰、计算过程更加简便、评价结果更合理和更符合偏联系数物理内涵的优势；②五元效应全偏联系数对农业旱灾脆弱性指标的诊断结果与实际情况相符，诊断出的4个评价指标年际变化较大，且对旱灾脆弱性综合评价结果的影响较为明显。五元效应全偏联系数的提出扩展了效应全偏联系数的研究广度，应用在不同实例中得出了较为合理的计算结果，在解决自然风险研究中的类似问题有较大的应用前景。

水问题；趋势分析；联系数；五元效应全偏联系数；偏正联系数；偏负联系数；趋势曲线

0 引言

【研究意义】受气候变化的自然因素和需水量增加的人为因素双重影响所导致的水旱灾害、水环境污染等水问题日益凸显，相关研究方法和模型定量化的方法，可为科学有效地解决一系列水问题提供科学指导。【研究进展】葛岩等[1]在研究修正后指数方法的基础上，耦合克里金空间插值法和小波分析法分析了辽西北地区的干旱时空特性；徐东梅等[2]提出了基于改进灰色聚类的农业旱灾脆弱性评价模型，对湖南省多个地区农业旱灾脆弱性的评价等级进行排序；张向明等[3]分别以和为水文干旱指标，识别出的干旱历时、干旱强度和干旱强度峰值为干旱特征变量，用Copula函数对黑河流域的水文干旱做了研究。以上方法的提出取得了有益成果，同时存在一些不足之处，如上述方法尚不能同时描述研究对象的确定性和不确定性特征及其发展趋势。【切入点】集对分析[4]是通过对立统一的关系描述事物确定性不确定性特征的一种新颖系统分析方法，经过相关学者不断努力取得一系列研究成果，周戎星等[5]用集对分析方法对山东省水量进行预测；徐建新等[6]用集对分析方法评价了城市节水型社会建设规划；HOU等[7]构建了基于集对分析的集成代理模型，并应用于重非水相液体污染含水层修复策略优化比较中；LI等[8]建立了集对分析和均值聚类分析的综合评估模型，并用于水污染风险评估；YU等[9]用改进的五元联系数方法对水质做了综合评价；潘争伟等[10]用集对分析法建立了水资源环境系统脆弱性分析方法。上述研究成果是集对分析方法研究事物在宏观层面上的相对变化，而为研究事物在微观层次上的变化，赵克勤在2005年提出了联系数[4]的伴随函数——偏联系数[11]，可通过研究微观因子的作用和变化来研究评价对象发展趋势，这些趋势是由偏正联系数和偏负联系数共同作用的结果。偏正联系数表征研究对象正向的发展趋势，偏负联系数表征负向的发展趋势，全偏联系数表征集对事件整体的发展趋势[11]。目前偏联系数在多个领域取得重大发展：赵克勤等[11-12]利用偏联系数描述发展趋势，提供了一种研究系统发展观的理论模型。蒯仂等[13]将偏联系数应用于寻常型银屑病对症用药优选问题中，为提高治疗效果提供了新方案。李辉等[14]采用偏联系数对安徽省水资源承载力进行了动态诊断研究，识别出水资源承载力的脆弱性指标。晏燕等[15]以五元偏联系数为基础，构建了集对分析的隐私风险评估模型，有效克服了动态指标在评价过程中的不确定性、随机性和模糊性等问题。杨红梅等[16]阐述了常用的二元至五元联系数的偏联系数的最新算法思路。金菊良等[17]研究了联系数的一阶偏联系数和减法集对势的现有成果，并考虑偏正联系数与偏负联系数中差异度系数具有方向性，在此基础上提出了三元联系数的效应全偏联系数。三元效应全偏联系数根据比例取值法确定的取值，偏正联系数中取正值，表示“正效应”，偏负联系数中取负值，表示“负效应”[17]。若三元效应全偏联系数值大于0则表示集对事件有正向发展的趋势，小于0则表示集对事件有负向发展的趋势，等于0则表示集对事件处于临界发展的趋势。现有的研究多采用多阶（2阶或2阶以上）的偏联系数分析集对事件的发展趋势[13,16]、认为多阶求导可消去差异度系数，然而正是由于差异度系数的存在，集对事件才会隐涵正负发展方向不确定的重要信息，所以现有偏联系数计算方法中以多阶偏联系数判断集对事件的发展趋势缺乏合理性。【拟解决的关键问题】一阶全偏联系数的结果表示集对事件的发展趋势，二阶全偏联系表示集对事件往正向/负向发展趋势的速率，阶全偏联系数的含义依次类推。五元联系数目前在系统综合评价中应用广泛，为此本文重点研究五元联系数的一阶效应全偏联系数，类比三元效应全偏联系数的基本理论和公式，推导出五元效应全偏联系数的计算公式和物理内涵，同时用一阶效应全偏联系数的趋势曲线的面积加以解释效应全偏联系数。效应全偏联系数可较为充分地揭示集对事件趋势的发展，可为集对事件后续的防控与管理做好前期准备，同时在其他类似的趋势分析问题中也有广泛的应用前景。

1 效应全偏联系数

1.1 三元效应全偏联系数

鉴于三元联系数的效应全偏联系数已有研究[17]，所以这里以三元效应全偏联系数为基础进行阐述。从事物不断发展变化的观点来看，三元联系数=++中假设差异度原本也是处在对立度上，是对立度往正向发展而来，用∂B=/（+）表示原本处在对立度上的事物正向发展到差异度上的比例；同理可用∂A=/（+）表示原本处在差异度上发展到同一度上的比例；三元联系数=++的效应偏正联系数可定义为[11,16-17]：

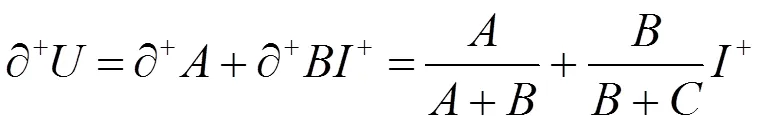
式中：+的取值一般按比例取值法[10,17]。+=∂A/(∂A+∂B)，+∈[0,1]。偏正联系数表明集对事件往正向的发展趋势，数值越大表示事件往正向发展的趋势越显著，I表示在偏正联系数中起“正效应”的作用[10]｡

由对立统一的观点知事物具有辩证性，可参照偏正联系数来定义偏负联系数｡假设差异度原本是处在同一度的层次上，是同一度向负向发展而来，用∂B=/(+)表示原本处在同一度上的事物发展到差异度上的比例；同理可用∂C=/(+)表示原本处在差异度上的事物发展到对立度上的比例；三元联系数=++的效应偏负联系数∂U可定义为[17]：

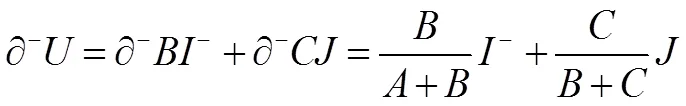
式中：=-1，-的取值一般按比例取值法[10,17]取-= -∂C/(∂B+∂C)，-∈[-1,0]，偏负联系数表明集对事件往负向的发展趋势，数值越小表示事件往负向发展的趋势越大，I表示在偏负联系数中起“负效应”[10]的作用｡集对事件的发展方向一般是由整个系统内各个方面综合作用决定事件的发展趋势，据此可得出效应全偏联系数为[17]：

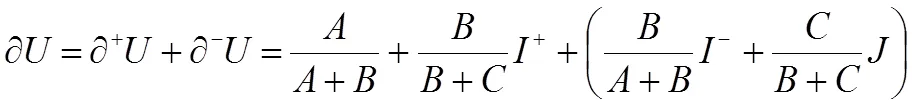
式中：当>0时，集对事件有正向发展趋势；当<0时，事件有负向发展趋势；当=0时，事件的发展趋势是不确定的，处于临界状态，可能往正向也可能往负向发展[17]。式（3）中差异度系数一般按照比例取值法取值，故进一步化简得[17]：

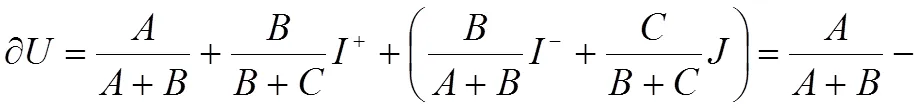
1.2 五元效应偏联系数

类似式（1），可得五元联系数的效应偏正联系数为：

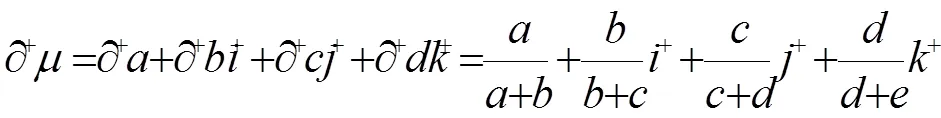
式中：+=∂a/(∂a+∂b)，+=∂a/(∂a+∂c)，+=∂a/(∂a+∂d)，+、+、+∈[0,1]。

类似式（2），可得五元联系数的效应偏负联系数为：

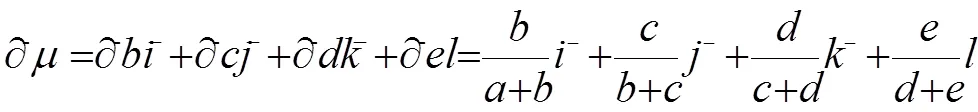
式中：-=-∂e/(∂b+∂e)，-=-∂e/(∂c+∂e)，-= -∂e/(∂d+∂e)，-、-、-∈[-1,0]，=-1。

类似式（3），可得五元联系数的效应全偏联系数为：

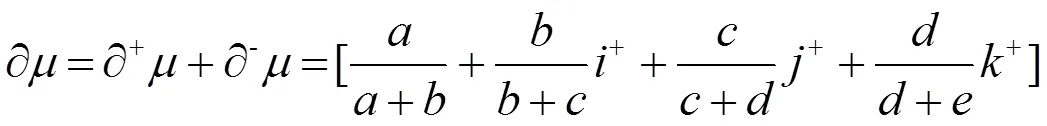
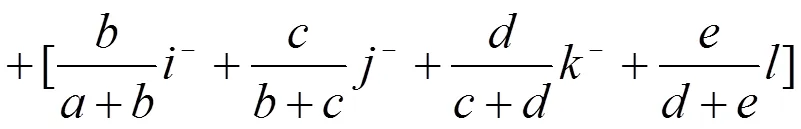
1.3 三元与五元效应全偏联系数间的关系

三元效应全偏联系数（式（3））与五元效应全偏联系数（式（7））的相同点是在结构形式上是一致的，其都是综合偏正联系数和偏负联系数得来，差异度系数都是按比例取值法确定；不同点主要是三元和五元表示的维度不一样，三元联系数只有1个不确定度，五元联系数有3个不确定度，五元是在三元的基础上按照同异反的思路推演而来的。针对不同的问题，我们可以按照三元和五元的效应全偏联系数的性质和特点选取适当的方法。在一定程度上，三元表达的形式更简单一些，计算更加方便；五元虽然相对比较复杂，但是刻画的问题也会更加细致。

1.4 效应全偏联系数的趋势曲线

综上1.1、1.2小节所述，按照效应偏正联系数与效应偏负联系数在不同层次发展趋势的基础上，相加得到元效应全偏联系数，同时差异度系数均按照正、负效应取值。为全面准确直观地表述效应全偏联系数，以五元效应全偏联系数为例，可用趋势曲线的面积表示集对事件的发展趋势[18]，如图1所示。

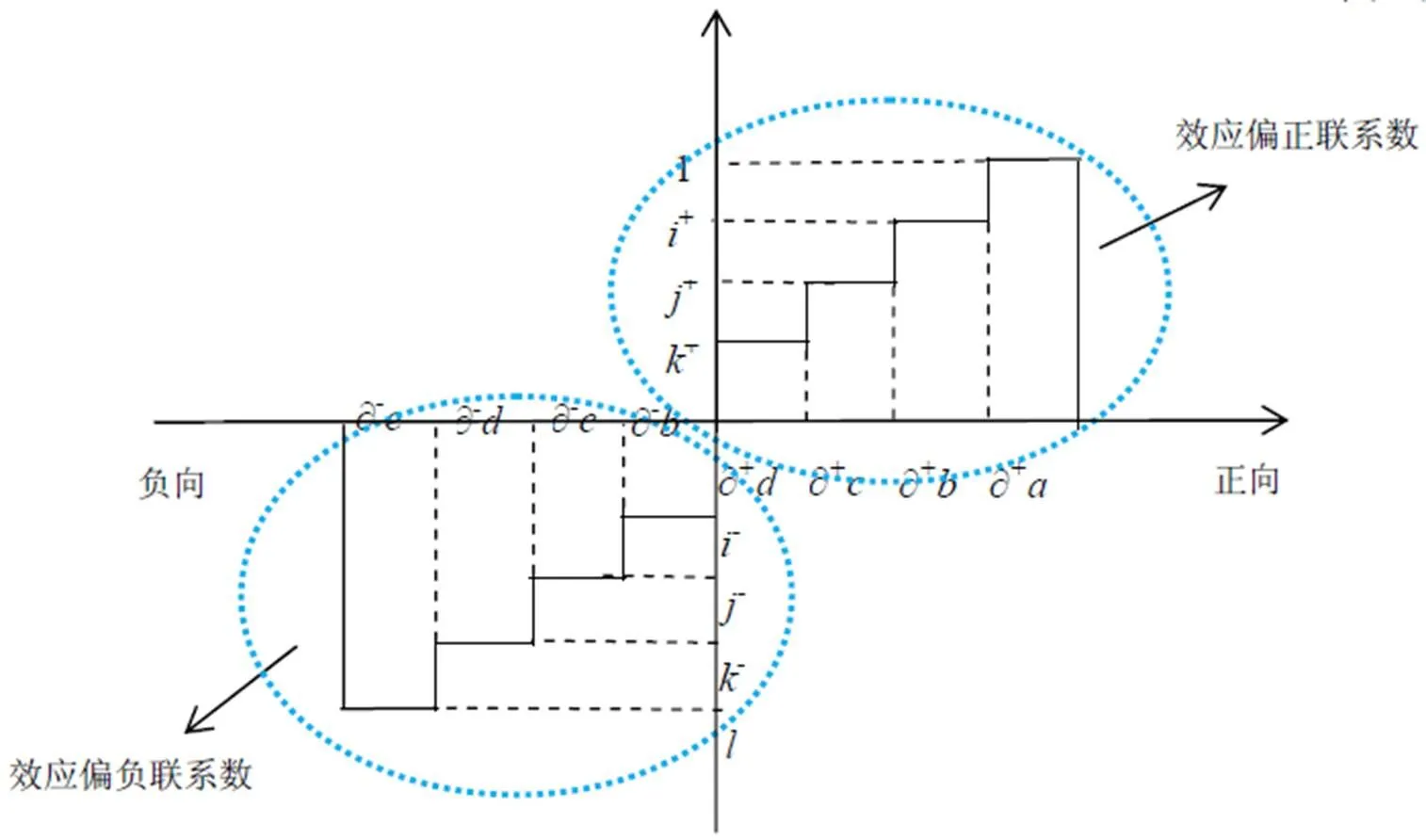
图1 效应全偏联系数的趋势曲线面积

图1中，坐标原点表示正负方向发展趋势的初始点，横坐标中“正向”表示集对事件往正向发展的趋势，“负向”表示事件往负向发展的趋势，正负仅仅表示事件发展的方向。横坐标上的数字全为正数，∂a∂b∂c∂d表示正向发展趋势的程度大小，它们之间无固定的大小关系，仅与各联系度分量本身的大小有关，1、i、j、k分别表示对应的正向发展趋势的确定度，表示正效应强度，强度越大距离原点越远，i、j、k之间无固定的大小关系，但都在0到1之间，1的正效应强度最大；∂e∂d∂c∂b表示负向发展趋势的程度大小，它们之间无固定的大小关系，仅与各联系度分量本身的大小有关，、k、j、i分别表示对应的负向发展趋势的确定度，表示负效应强度，强度越大距离原点越远，i、j、k之间无固定的大小关系，但都在-1到0之间，的负效应强度最大。第一象限内实线与坐标轴所围成的面积（∂a+∂bi+∂cj+∂dk）表示效应偏正联系数的值，第三象限内实线与坐标轴所围成的面积（-∂e+∂dk+∂cj+∂bi）表示效应偏负联系数的值，二者之和就是效应全偏联系数的趋势曲线面积、该面积表示效应全偏联系数的值。

1.5 效应全偏联系数与减法集对势的关系

五元联系数的减法集对势为[19]：

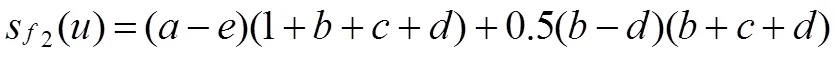
式中：当====0、=1时，（）min=-1，当====0时、=1时，（）max=1，()∈[-1,1]。五元减法集对势同样可以分为5个势级[19-20]：反势()∈[-1,-0.6)，偏反势()∈[-0.6,-0.2)，均势()∈[-0.2, 0.2]，偏同势()∈(0.2, 0.6]，同势()∈(0.6,1]。

效应全偏联系数与减法集对势二者具有相一致的物理内涵｡从微观层次上看，效应全偏联系数通过考虑联系数分量在微观层次上的演变关系，运用偏正联系数与偏负联系数之间的相对大小判断集对事件发展的整体趋势。从宏观层次上看，减法集对势通过联系数中同一度与对立度之间的关系，直接确定不确定性系数的取值方式，从宏观的角度得出集对事件发展的趋势。当和都等于0时，减法集对势仍然考虑差异度子项对于趋势的影响作用，而效应全偏联系认为无正负发展趋势，在一定程度上减法集对势表示得更准确些，但是当和等于0认为集对事件近似处于临界状态也是可行的，因为差异度对变化趋势的影响相比同一度和对立度要小。

2 应用实例

2.1 五元效应全偏联系数在水资源承载力评价中的应用

对收集到的四川省水资源承载力指标数据[21]用式（5）—式（7）计算得效应全偏联系数的计算结果（见表1）。

表1 水资源承载力联系数

为便于比较表1中2种偏联系数计算方法的差异，将表1的计算结果绘成趋势曲线图，如图2所示。

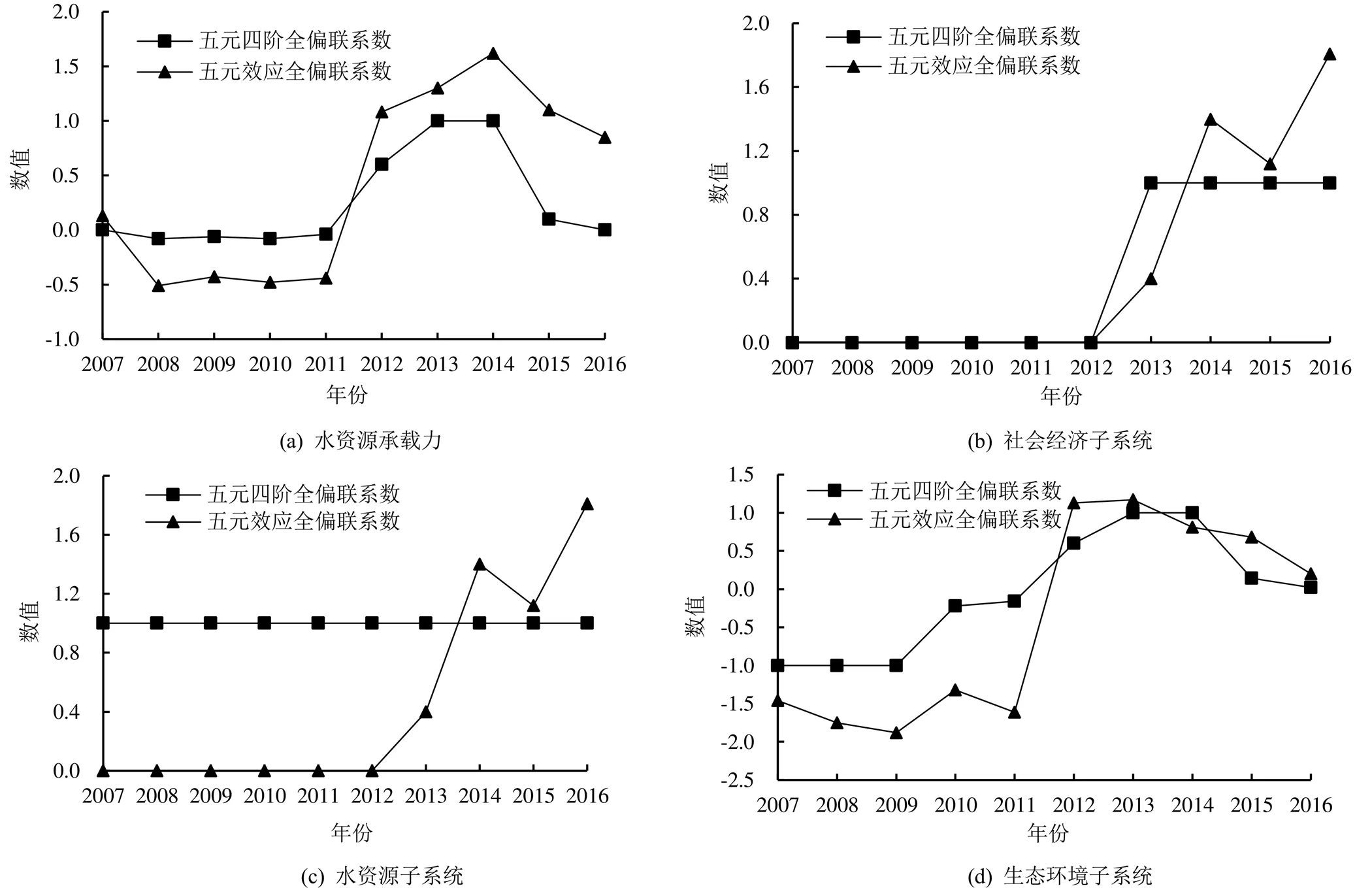
图2 水资源承载力及其子系统的趋势曲线

由表1计算结果和图2的趋势曲线可知，本文的五元效应全偏联系数计算结果和文献[21]中的五元四阶全偏联系数的计算结果的变化趋势基本一致：社会经济子系统在2007—2012年处于临界状态，2013—2016年处于正向发展趋势；水资源子系统从2007年到2016年全部处于正向发展趋势；生态环境子系统在2007—2011年处于负向发展趋势，但在2012年以后处于正向发展趋势；水资源承载力在2007—2011年大多处于负向发展状态，2012—2016年基本变成正向发展趋势，且同一度由2007年的0.19发展成为2016年的0.43，对立度由2007年的0.16降低为2016年0.07，故判断总体是呈正向发展的趋势是合理的。由社会经济子系统2007年到2012年的评价结果可知：当同一度=0时，效应偏正联系数计算的结果为0；当对立度=0时，效应偏负联系数计算的结果为0；当同一度和对立度同时为0时，计算的效应全偏联系数为0，表明这些年的社会经济子系统处于临界状态，这也是符合实际情况的。

五元效应全偏联系数和文献[21]中的五元四阶全偏联系数的不同点主要在于：

1）文献[21]中的五元四阶全偏联系数是通过逐次偏联系数的方式消除差异度系数，虽然从数学运算上看求偏消除差异度系数的思路符合数学中的求偏定理，但是差异度系数是反映联系数表达不确定性的重要方面，通过求偏消除差异度系数与联系数同时考虑确定性不确定性、确定性不确定性可以相互转换的重要思想不一致，不能有效表达和利用集对事件的不确定性信息。而五元效应偏联系数是通过三元效应偏联系数推广而来，只需对联系数求一次偏联系数，再通过比例取值法确定各差异度系数即可求解五元联系数的发展趋势，能有效表达集对事件的确定性和不确定性，思路清晰，计算简便，评价结果合理，也更符合联系数的求偏的基本定义和物理意义。

2）五元四阶全偏联系数的取值范围在-1到1之间，最小等于-1，最大等于1；五元全偏联系数计算结果突破了这个范围的限定，可更细致地对各评价样本的发展趋势进行比较和排序，例如对于表1中水资源承载力的2013年和2014年2个样本，五元四阶全偏联系数得计算结果都等于1，而五元效应全偏联系数计算结果分别为1.30和1.62，说明2014年水资源承载力正向变化趋势大于2013年的变化趋势。由此可见，五元效应全偏联系数可比五元四阶全偏联系数更细致地表达集对事件的发展趋势。

3）在水资源承载力评价中，2种方法对2007年和2016年的评价结果有一定差异，五元四阶全偏联系数对这2 a的评价结果为临界发展状态，而五元效应全偏联系数对这2 a的评价结果为正向发展状态。2016年的联系数2016=0.43+0.16+0.18+0.16+0.07，（+）明显大于（+），在此样本中，联系数分量既不是对称的形式，也不符合上述所说的同一度和对立度=0的情况，但是五元四阶全偏联系数的偏正联系数为0.50、偏负联系数为0.50，全偏联系数为0，综合评价结果处于临界状态，这明显与实际情况不符合；而用效应偏联系数计算的偏正联系数为1.68，偏负联系数为0.83，全偏联系数为0.85，综合评价结果为正向发展趋势，显然更符合实际情况。

综上所述，本文提出的五元效应偏联系数评价方法是合理的，且相比文献[21]中的评价方法更简便合理，适用性更强。

2.2 五元效应全偏联系数在农业旱灾脆弱性趋势分析中的应用

采用文献[22]计算的蚌埠市2001—2010年4个农业旱灾脆弱性评价指标的五元联系数各联系数分量的计算结果如表2所示。

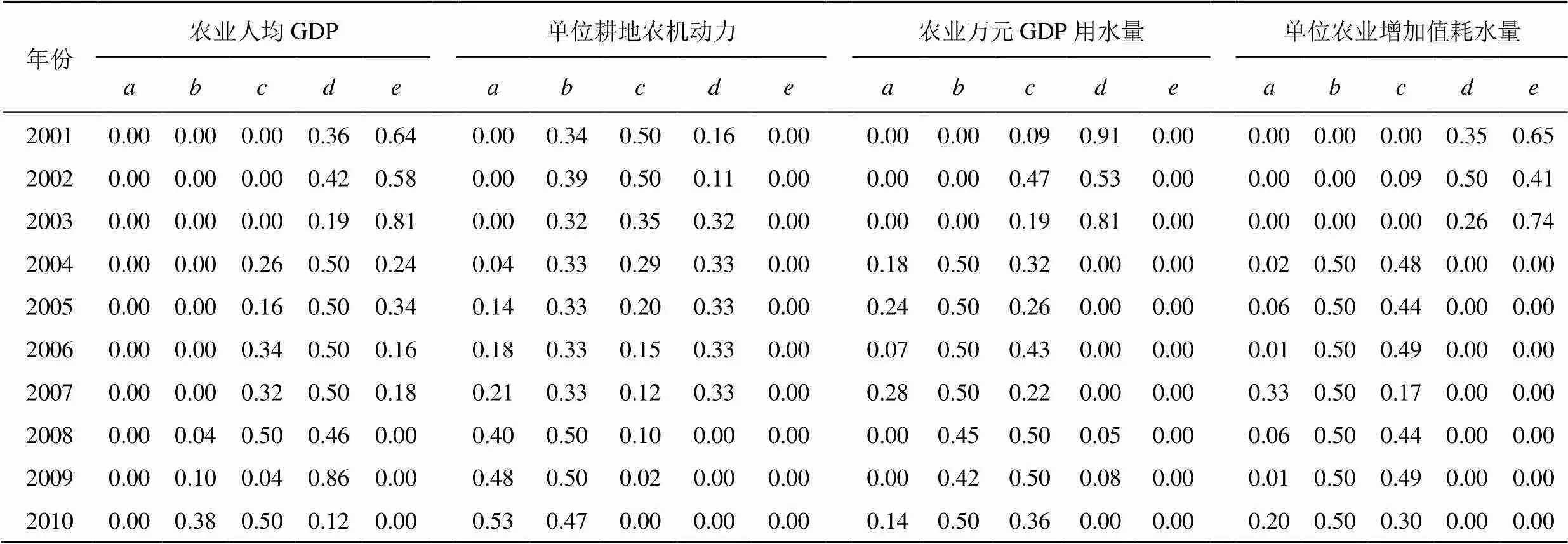
表2 4种旱灾脆弱性指标的联系数分量[22]

根据表2中4个旱灾脆弱性指标各年的联系数值，运用式（5）—式（8）计算各指标的效应全偏联系数、减法集对势值，用文献[6,21]中的方法计算五元四阶全偏联系数值，将计算的结果绘成折线图并进行相互比较，如图3（a）—图3（d）所示。

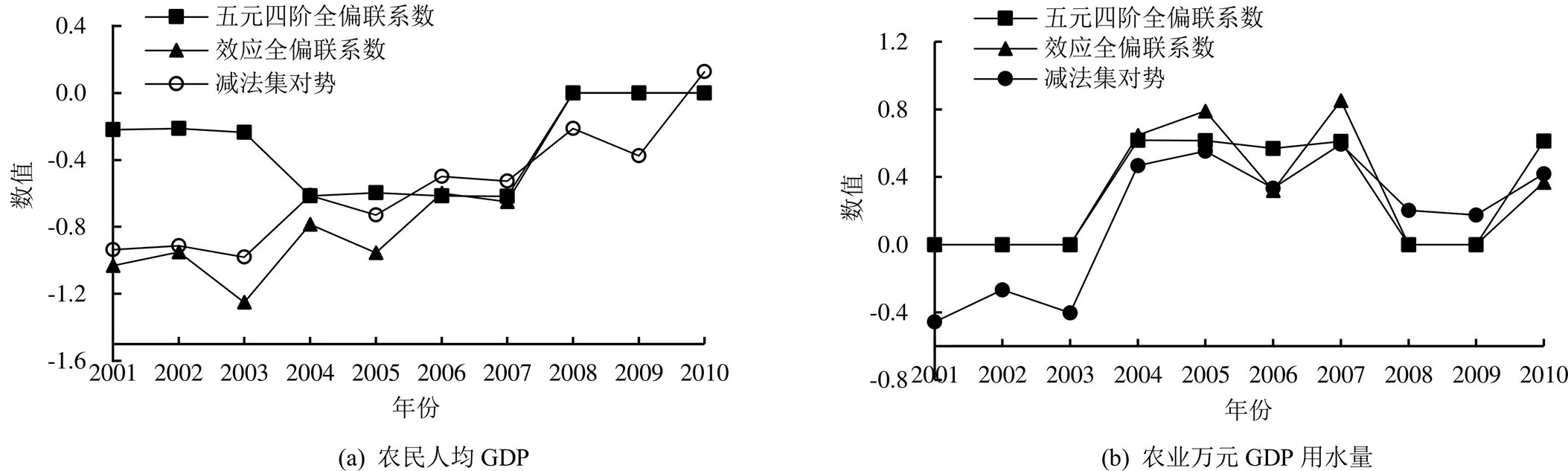
由图3（a）—图3（d）可知：

1）4种农业旱灾脆弱性诊断指标的效应全偏联系数、五元四阶全偏联系数和减法集对势结果值在变化趋势上基本一致，如：指标“单位耕地面积农机动力”随着时间的推移整体呈递增趋势；指标“农业万元GDP用水量”和“单位农业增加值耗水量”随着时间的推移整体在波动中呈递增趋势；指标“农民人均GDP”的效应全偏联系数和减法集对势在时间序列上呈递增趋势，五元四阶全偏联系数诊断结果在2001—2003年与另外2种方法的结果虽然不太一样，但是3种方法对该指标的诊断结果表现为负向发展趋势，只是变化程度存在一些差异。

2）对于2001—2003年的指标“农民人均GDP”和2001年的“单位农业增加值耗水量”五元四阶全偏联系数的评价结果相比其他2种方法的负向发展趋势要小得多，但是这些年份指标的联系数分量===0，和的值都比较大，表现出明显的负向趋势，所以效应全偏联系数和减法集对势的诊断结果更符合实际情况。

3）效应全偏联系数的评价结果的取值范围相比其他两种方法的结果一般更大些，可更明显地反映出指标的变化趋势，评价结果更直观可信。

4）4种农业旱灾脆弱性诊断指标中有3种指标的效应全偏联系数值略大于减法集对势计算的结果，且在某些年份相差较大，五元四阶全偏联系数与其他两种方法没有确定的大小关系，但是在各指标的各年评价中，3种方法计算结果判断集对事件发展的正负趋势基本是相一致的，说明3种方法对于指标诊断的发展趋势是基本一致的。

5）对于2001—2003年指标“农业万元GDP用水量”效应全偏联系数和五元四阶全偏联系数的诊断结果为临界状态，而减法集对势诊断结果为负向发展趋势，在减法集对势的式（8）中，当==0时仍然考虑差异度子项对于趋势的影响作用，而效应全偏联系数和五元四阶全偏联系数在==0的情况下认为无正负发展趋势，在一定程度上减法集对势表示得更准确些，但是当==0时可认为集对事件近似处于临界状态也是合理的，因为差异度对变化趋势的影响相比同一度和对立度要小很多。

6）指标“农民人均GDP”的效应全偏联系数值逐年增加趋势显著，这样的计算结果与农民实际GDP的增长情况相吻合，未出现矛盾情况。指标“农业万元GDP用水量”在2003年以变化趋势相对稳定，2003年以后显示出较强的正向发展趋势，且数值波动性较大，对于总体趋势的判断无明显影响。指标“单位耕地面积农机动力”数值始终≥0，2003—2009年有断崖式增长，说明在此期间农业机械自动化程度有了较大提升，计算结果与指标的逐年向好性保持一致。指标“单位农业增加值耗水量”在2004年以前始终＜0，2004年以后数值虽然＞0，但数值未呈现出较大增长，表明此指标各年的稳定性较差，未出现明显的正向发展趋势。

3 讨论

3.1 本文研究的突破点

①本文在三元效应全偏联系数的基础上研究五元联系数的效应偏联系数，计算的结果符合实际情况，将其用于四川省水资源承载力的诊断评价中，得出五元效应全偏联系数评价结果与五元四阶全偏联系数的评价结果基本一致，五元四阶全偏联系数需要通过四次求偏联系数来消除差异度系数，而五元效应全偏联系数只需对联系数求一次偏联系数，再通过比例取值法确定各差异度系数即可求解五元联系数的发展趋势。②进一步将五元效应全偏联系数用于蚌埠市农业旱灾脆弱性4种指标的诊断，得出五元效应全偏联系数与减法集对势的诊断结果、变化趋势基本一致，有效分析诊断了蚌埠市农业旱灾脆弱性指标的变化趋势并与实际情况作对比，减法集对势在==0时仍然考虑差异度子项对于趋势的影响作用，而效应全偏联系数和五元四阶全偏联系数在==0时认为无正负发展趋势，在一定程度上减法集对势表示得更准确些，但是当和等于0时可认为集对事件近似处于临界状态也是合理的，因为差异度对变化趋势的影响相比同一度和对立度要小很多，五元效应全偏联系数反映的变化趋势更加明显，更加直观。

3.2 本研究说明的问题

五元效应全偏联系数相当于联系数的一阶导函数，计算值反映的是事物变化趋势，可用于集对事件在微观上的诊断识别，可以试图在一阶求导的基础上进行二次求导来研究事物的变化的快慢，相当于速度的导数，即加速度，可以用来描述引起集对事件变化作用力的大小。

4 结论

本文在对三元效应全偏联系数进行深化研究的基础上，引入偏联系数的趋势曲线概念，更加系统清晰地阐述了效应全偏联系数的内涵，同时进一步深入分析了差异度系数的正、负效应及集对事件正、负方向发展趋势判别问题，从而推广到五元效应全偏联系数的研究中，并将研究成果进行实例分析，将评价结果与五元四阶全偏联系数和减法集对势的评价结果相比较，结果表明：①效应全偏联系数计算过程更简便，评价结果更合理；正是由于差异度系数的存在，集对事件才会隐含正负发展方向不确定的重要信息，所以用五元四阶偏联系数判断集对事件的发展趋势缺乏合理性，而五元效应全偏联系数通过比率取值法确定差异度系数更能细致地反映各评价对象之间的差异性，也更符合偏联系数的物理内涵。②五元效应全偏联系数和减法集对式各有优势，在研究集对事件的发展趋势时，可以同时用两种方法综合评价，对比分析。③效应全偏联系数能深刻地刻画集对事件的整体发展趋势，取得的结果值变化幅度相对较大，这样更能凸显连续年份间不同的变化趋势，对于不同情况下多种多元联系数可相互转化计算，适用范围更广且结果值较为针对性地显示出集对事件的发展趋势。

[1] 葛岩, 李趋, 褚丽妹, 等. 基于修正Z指数辽西北地区干旱时空特性分析[J]. 灌溉排水学报, 2013, 32(5): 133-136.

GE Yan, LI Qu, CHU Limei, et al. Temporal and spatial analysis on drought events in northwest of Liaoning based on adjusted Z-index[J]. Journal of Irrigation and Drainage, 2013, 32(5): 133-136.

[2] 徐冬梅, 李璞媛, 王文川, 等. 基于改进灰色聚类方法的农业旱灾脆弱性分析[J]. 灌溉排水学报, 2016, 35(8): 87-91.

XU Dongmei, LI Puyuan, WANG Wenchuan, et al. Analysis on vulnerability of agricultural drought disaster based on the improved grey clustering method[J]. Journal of Irrigation and Drainage, 2016, 35(8): 87-91.

[3] 张向明, 粟晓玲, 张更喜. 基于SRI与Copula函数的黑河流域水文干旱等级划分及特征分析[J]. 灌溉排水学报, 2019, 38(5): 107-113.

ZHANG Xiangming, SU Xiaoling, ZHANG Gengxi. Classifying drought in Heihe basin using SRI index and copula function[J]. Journal of Irrigation and Drainage, 2019, 38(5): 107-113.

[4] 赵克勤. 集对分析及其初步应用[M]. 杭州: 浙江科学技术出版社, 2000.

ZHAO Keqin. Set pair analysis and its preliminary application [M]. Hangzhou: Zhejiang Science & Technology Press, 2000.

[5] 周戎星, 潘争伟, 金菊良, 等. 集对分析相似预测在用水量预测中的应用[J]. 华北水利水电大学学报(自然科学版), 2016, 37(6): 67-71.

ZHOU Rongxing, PAN Zhengwei, JIN Juliang, et al. Application of the method of set pair analysis based on similarity forecast model in water consumption prediction[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2016, 37(6): 67-71.

[6] 徐建新, 赵鹏, 陆建红, 等. 城市节水型社会建设规划评价的集对分析[J]. 华北水利水电学院学报, 2010, 31(3): 1-4.

XU Jianxin, ZHAO Peng, LU Jianhong, et al. Set pair analysis method applied to evaluate water-saving society planning[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power, 2010, 31(3): 1-4.

[7] HOU Z Y, LU W X, XUE H B, et al. A comparative research of different ensemble surrogate models based on set pair analysis for the DNAPL-contaminated aquifer remediation strategy optimization[J]. Journal of Contaminant Hydrology, 2017, 203: 28-37.

[8] LI C H, SUN L, JIA J X, et al. Risk assessment of water pollution sources based on an integrated k-means clustering and set pair analysis method in the region of Shiyan, China[J]. Science of the Total Environment, 2016, 557: 307-316.

[9] YU F R, QU J H, LI Z P, et al. Application of set pair analysis based on the improved five-element connectivity in the evaluation of groundwater quality in Xuchang, Henan Province, China[J]. Water Science and Technology: Water Supply, 2017, 17(3): 632-642.

[10] 潘争伟, 周戎星, 戚晓明, 等. 水资源环境系统脆弱性分析及评价方法研究[J]. 华北水利水电大学学报(自然科学版), 2018, 39(4): 72-78.

PAN Zhengwei, ZHOU Rongxing, QI Xiaoming, et al. Evaluation method research and vulnerability analysis of water resources environmental system[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2018, 39(4): 72-78.

[11] 赵克勤. 偏联系数[A]. 中国人工智能进展 2005[C]. 北京: 北京邮电大学出版社, 2005: 884-885.

ZHAO Keqin. Partial connection number[A]. Progress of artificial intelligence in China 2005[C]. Beijing: Beijing University of Posts and Telecommunications Press, 2005: 884-885.

[12] 赵克勤, 张清河. 基于联系数的同异反系统和谐与发展理论探讨[C].厦门: 中国系统工程学会第十四届学术年会论文集, 2006: 215-220.

ZHAO Keqin, ZHANG Qinghe. Discussion on the theory of harmony and development of identical, different and opposite systems based on connection number[C]. Xiamen: The 14th Annual Meeting of Chinese Society of Systems Engineering, 2006.

[13] 蒯仂, 赵克勤, 李斌. 基于集对分析偏联系数的寻常型银屑病对症用药优选探讨[J]. 上海医药, 2018, 39(23): 9-14, 67.

KUAI Le, ZHAO Keqin, LI Bin. Optimization of symptomatic medication for psoriasis vulgaris based on set-pair analysis and partial correlation coefficient[J]. Shanghai Medical & Pharmaceutical Journal, 2018, 39(23): 9-14, 67.

[14] 李辉, 金菊良, 吴成国, 等. 基于联系数的安徽省水资源承载力动态诊断评价研究[J]. 南水北调与水利科技, 2018, 16(1): 42-49.

LI Hui, JIN Juliang, WU Chengguo, et al. Dynamic evaluation and diagnostic analysis for water resources carrying capacity in Anhui Province based on connection number[J]. South-to-North Water Transfers and Water Science & Technology, 2018, 16(1): 42-49.

[15] 晏燕, 王万军. 偏联系数隐私风险态势评估方法[J]. 计算机工程与应用, 2018, 54(10): 143-148.

YAN Yan, WANG Wanjun. Privacy risk situation assessment method based on partial connection numbers[J]. Computer Engineering and Applications, 2018, 54(10): 143-148.

[16] 杨红梅, 赵克勤. 偏联系数的计算与应用研究[J]. 智能系统学报, 2019, 14(5): 865-876.

YANG Hongmei, ZHAO Keqin. The calculation and application of partial connection numbers[J]. CAAI Transactions on Intelligent Systems, 2019, 14(5): 865-876.

[17] 金菊良, 张浩宇, 宁少尉, 等. 效应全偏联系数及其在区域水资源承载力评价中的应用[J]. 华北水利水电大学学报(自然科学版), 2019, 40(1): 1-8.

JIN Juliang, ZHANG Haoyu, NING Shaowei, et al. Effect full partial connection number and its application in evaluation of regional water resources carrying capacity[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2019, 40(1): 1-8.

[18] 许逊哲, 蒯仂, 茹意, 等. 基于集对分析疗效曲线与偏联系数的银屑病用药优选探讨[J]. 中华中医药学刊, 2018, 36(8): 1 822-1 825.

XU Xunzhe, KUAI Le, RU Yi, et al. Optimization of psoriasis medication based on set pair analysis, efficacy curve and partial correlation coefficient[J]. Chinese Archives of Traditional Chinese Medicine, 2018, 36(8): 1 822-1 825.

[19] 金菊良, 陈鹏飞, 张浩宇, 等. 五元减法集对势及其在水资源承载力趋势分析中的应用[J]. 华北水利水电大学学报(自然科学版), 2020, 41(2): 1-7.

JIN Juliang, CHEN Pengfei, ZHANG Haoyu, et al. Five element subtraction set pair potential and its application in trend analysis of water resources carrying capacity[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2020, 41(2): 1-7.

[20] 金菊良, 沈时兴, 郦建强, 等. 基于联系数的区域水资源承载力评价与诊断分析方法[J]. 华北水利水电大学学报(自然科学版), 2018, 39(1): 1-9.

JIN Juliang, SHEN Shixing, LI Jianqiang, et al. Assessment and diagnosis analysis method for regional water resources carrying capacity based on connection number[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2018, 39(1): 1-9.

[21] 刘童, 杨晓华, 赵克勤, 等. 基于集对分析的水资源承载力动态评价:以四川省为例[J]. 人民长江, 2019, 50(9): 94-100.

LIU Tong, YANG Xiaohua, ZHAO Keqin, et al. Dynamic evaluation of water resources carrying capacity based on set pair analysis: A case study of Sichuan Province[J]. Yangtze River, 2019, 50(9): 94-100.

[22] 金菊良, 张浩宇, 陈梦璐, 等. 基于灰色关联度和联系数耦合的农业旱灾脆弱性评价和诊断研究[J]. 灾害学, 2019, 34(1): 1-7.

JIN Juliang, ZHANG Haoyu, CHEN Menglu, et al. Evaluation and diagnosis of agricultural drought vulnerability based on grey correlation and connection number coupling[J]. Journal of Catastrophology, 2019, 34(1): 1-7.

The Effect Full Partial Connection of Five Element Connection Number and Its Application in Trend Analysis of Water Problems

JIN Juliang1,2, XU Jirong1,2, CHEN Menglu1,2*, ZHANG Haoyu1,2, NING Shaowei1,2, CHEN Pengfei1,2

(1. School of Civil Engineering and Water Conservancy Engineering, Hefei University of Technology, Hefei 230009, China; 2. Institute of Water Resources and Environmental Systems Engineering, Hefei University of Technology, Hefei 230009, China)

In previous work, we studied the results of the first-order partial connection coefficient and the subtraction set pair potential of the connection number, where we considered the directionality of the difference coefficientin the partial positive connection number and the partial negative connection number. 【】The aim of this paper is to clarify the definition of the total partial coupling coefficient of the five element effect, determine its expression formula, describe its physical connotation, and evaluate its practical application in solving real water problems. 【】This paper uses the method of analogy analysis to determine the calculation formula of the total partial coefficient of the five element effect by analyzing the existing results of the total partial coefficient of the three element effect, and further explains the physical connotation of the total partial coefficient of the five element effect with the help of the area of the trend curve of the partial coefficient, and applies it to the actual analysis of water problems.【】①the results of the dynamic evaluation of water resources carrying capacity in Sichuan Province are highly consistent with the results of the full deflection coefficient of five element effect, and the full deflection coefficient of five element effect has the advantages of clearer development trend of the evaluation object, simpler calculation process, more reasonable evaluation results and more consistent with the physical connotation of the deflection coefficient; ②The diagnostic results of the five element effect partial coefficient on the vulnerability index of agricultural drought are consistent with the actual situation. The four indicators have great intraannual changes, and the impact on the comprehensive assessment results of drought vulnerability is more obvious.【】The proposal of the five element effect total partial coupling coefficient expands the research scope of the effect total partial coupling coefficient, and the application in different cases has drawn more reasonable and credible calculation results, which has a great application prospect in solving similar problems in natural risk research.

water problems; trend analysis; connection number; five-element effect full partial connection number; partial positive connection number; partial negative connection number; trend curve

金菊良, 许继荣, 陈梦璐, 等. 五元联系数的效应全偏联系及其在水问题趋势分析中的应用[J]. 灌溉排水学报, 2021, 40(9): 93-101.

JIN Juliang, XU Jirong, CHEN Menglu, et al. The Effect Full Partial Connection of Five Element Connection Number and Its Application in Trend Analysis of Water Problems[J]. Journal of Irrigation and Drainage, 2021, 40(9): 93-101.

TV213

A

10.13522/j.cnki.ggps.2019457

1672 – 3317（2021）09 - 0093 - 09

2019-12-22

国家重点研发计划项目（2017YFC1502405）；山东省重点研发计划项目（2017GSF20101）；国家自然科学基金项目（51709071，51579060）

金菊良（1966-），男，江苏吴江人。教授，博士，主要从事水旱灾害研究。E-mail: JINJL66@126.com

陈梦璐（1990-），女，安徽安庆人。博士研究生，主要从事水资源系统工程研究。E-mail: 516792688@qq.com

责任编辑：白芳芳