不同榫卯板构造的装配整体式剪力墙有限元模拟与参数分析

2021-10-14陈国尧刘继良曹春利李祥宾初明进

北京建筑大学学报 2021年3期

陈国尧, 刘继良, 曹春利, 李祥宾, 初明进

(1.北京建筑大学北京未来城市设计高精尖创新中心，北京 100044； 2.大连理工大学土木工程学院，大连 116024)

榫卯连接装配整体式剪力墙(以下简称榫卯剪力墙)[1-3]是一种新型装配整体式混凝土剪力墙结构，其以榫卯板为基本装配单元，榫卯板侧边间隔设置横向凹槽，并与侧边位置设置的纵向孔洞相交形成榫卯构造。榫卯板相互连接形成榫卯接缝，连接时将榫卯板的榫卯构造相对布置，通过在横向凹槽内放置连接钢筋、纵向孔洞内插入纵向钢筋，绑扎形成钢筋骨架，最后浇筑混凝土实现榫卯板水平方向的连接(图1)。

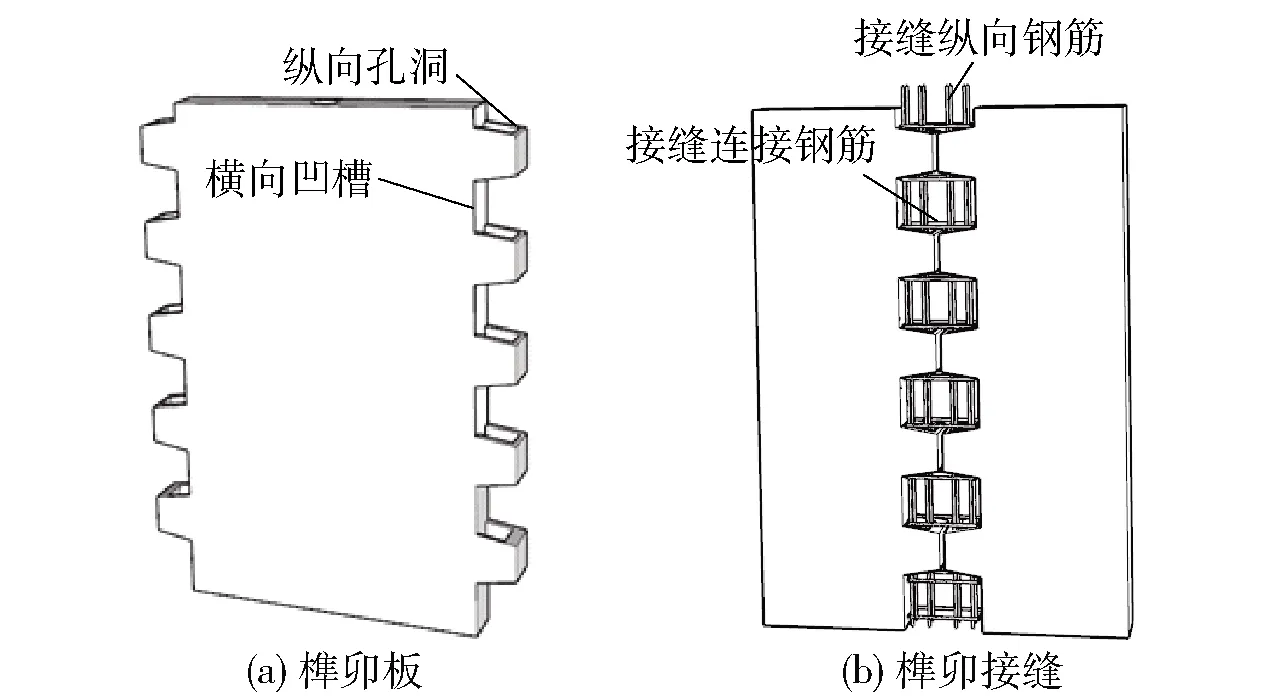
图1 榫卯剪力墙Fig.1 Monolithic precast integral concrete shear wall with mortise-tenon joints

榫卯板为不出筋构造，在构件生产、安装、运输等方面具备显著优势。试验结果表明，与后浇带连接技术相比，榫卯连接接缝具有更好的连接性能[4]。

接缝内后浇混凝土方柱与预制凸起部分的咬合作用影响着榫卯接缝的连接性能，而纵向孔洞的尺寸决定着方柱的体积及截面面积。文献[5]通过试验证明了榫卯板纵向孔洞内缘与横向凹槽内侧平齐的试件相比孔洞内缘深入预制板的试件在刚度及耗能上具有更好的表现，但未考虑孔洞内缘伸出预制板的情况。因此，在试验的基础上，采用有限元分析软件ABAQUS对榫卯剪力墙进行数值分析，研究不同纵向孔洞尺寸对榫卯接缝连接性能的影响，并对水平分布钢筋配筋率及轴压比与墙体性能的关系进行探讨。

1 试件设计

试件SPW- 1截面尺寸及配筋情况如图2所示。试验墙体截面尺寸为200 mm×1 500 mm，由榫卯板及中部榫卯接缝组成。榫卯板横向凹槽及横向凸起部分侧视图为等腰梯形，深度为150 mm，凹槽内、外侧长分别为200 mm、250 mm，凸起部分内、外侧长分别为200 mm、150 mm；纵向孔洞尺寸为130 mm×120 mm,内缘与横向凹槽内侧平齐。

图2 试件SPW- 1截面尺寸及配筋情况Fig.2 Specimen SPW- 1 geometric size and reinforcement configuration

试验混凝土平均抗压强度为：预制混凝土46.68 MPa，现浇混凝土31.71 MPa。实测钢筋屈服强度平均值fy,m、抗拉强度平均值fu,m和伸长率δm平均值见表1。

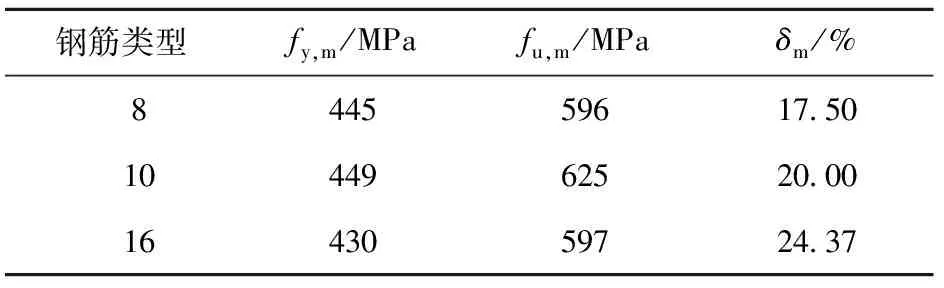
表1 钢筋材料性能

2 ABAQUS有限元模型的建立

2.1 单元及有限元模型

实体模型采用分离式微观有限元模型，对钢筋、预制混凝土、后浇混凝土分别建模。混凝土部分采用C3D8R实体单元，钢筋采用T3D2桁架单元，不考虑钢筋的黏结滑移作用，将钢筋嵌入混凝土中。试件模型及网格划分如图3所示。

图3 有限元模型Fig.3 Finite element model

2.2 本构模型

混凝土采用软件提供的混凝土损伤塑性模型。混凝土材料本构关系参照GB 50010—2010《混凝土结构设计规范》取用，边缘构件及中部现浇暗柱部分混凝土选用文献[6-7]提出的约束混凝土本构关系。

钢筋本构模型采用二折线模型及Vonmises准则，泊松比取0.3，屈服后弹性模量E′s=0.01Es(Es为弹性模量，取2×105N/mm2)。

2.3 结合面模拟

榫卯接缝连接性能对于榫卯剪力墙受力性能影响较大，接缝内存在的新旧混凝土结合面是墙体受力的薄弱环节，建立合理的新旧混凝土结合面模型是开展榫卯剪力墙数值分析的基础。剪切- 摩擦理论[8]将新旧混凝土结合面的界面剪力分为黏结力、界面钢筋销栓作用以及摩擦力。黏结力在结合面未分离时起主要作用，达最大黏结力时，结合面分离，产生摩擦力，同时钢筋随着界面相对位移的增加受拉，产生销栓作用提供销栓力[9]。

ABAQUS软件中“Surface to Surface”接触对中可进行黏性行为、损伤、切向行为及法向行为属性的定义，黏性和损伤可定义内聚力模型，切向可定义库伦- 摩擦模型，2个模型共同作用可形成内聚力- 摩擦模型[10]，该模型在初始时，内聚力模型弹性工作，结合面未发生分离，摩擦模型不参与工作。当达到损伤准则时结合面分离，摩擦模型介入，在结合面处按摩擦系数贡献剪应力，与内聚力模型共同工作。

黏性行为中由法向刚度Knn、切向刚度Kss、Ktt组成，各方向互不影响，在结合面接触受力曲线处于弹性段时满足τ=Kδ，其中τ为切向应力，K为刚度，δ为结合面分离量。新旧混凝土层在法向受压时不互相侵入，刚度理论上趋于无限大，根据文献[11]，Knn取值100 000 MPa/mm。

法向行为采用“Hard contact”，允许接触后分离。相关参数设置见表2。

表2 新旧混凝土结合面参数设置

3 基准模型

3.1 破坏形态对比

数值计算得到的最大主塑性应变云图与试件破坏形态对比如图4所示，其中破坏状态为水平荷载下降至峰值荷载85%时对应的状态点。对比可得：

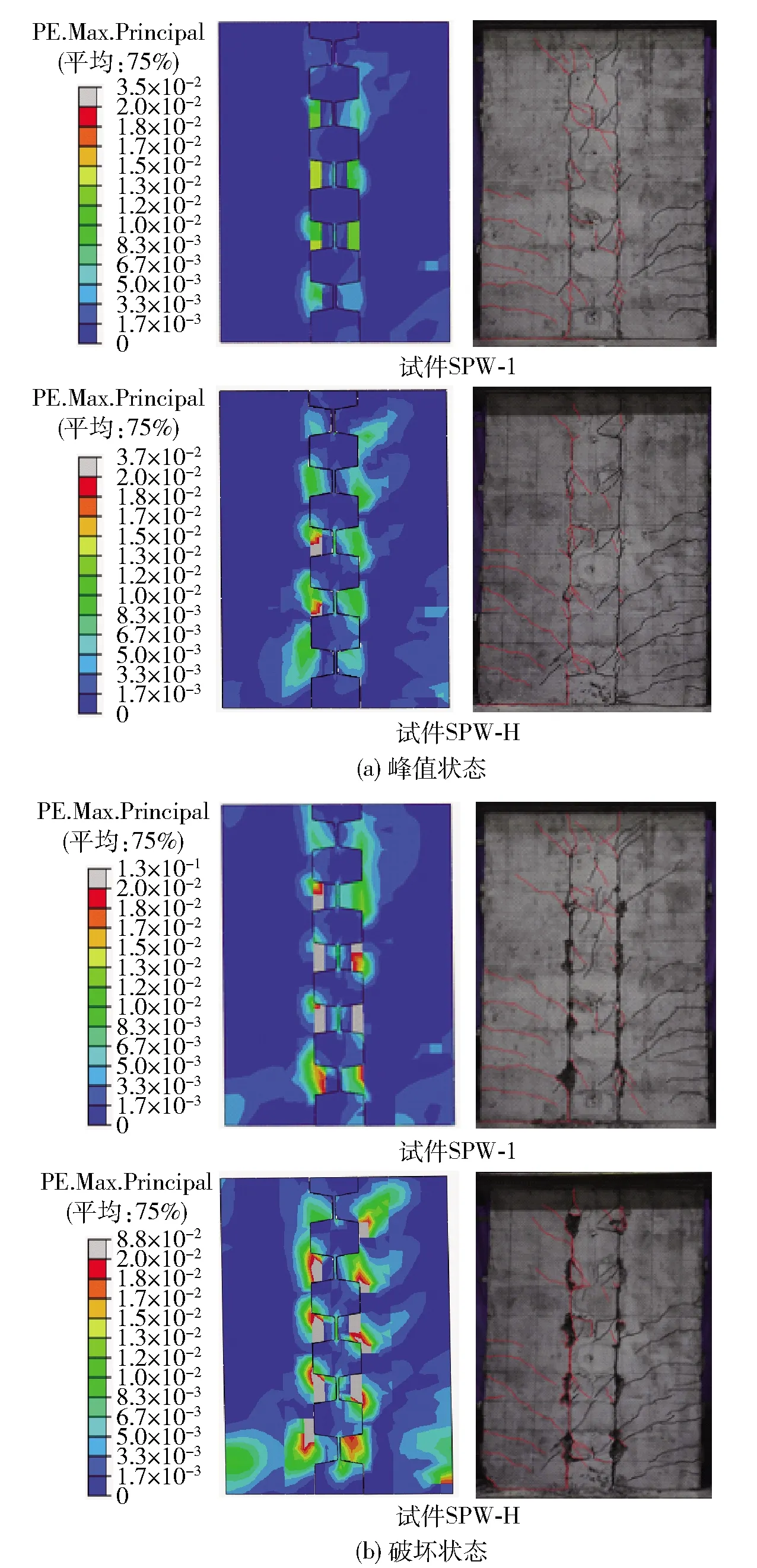
图4 数值分析与试验破坏形态对比Fig.4 Comparison of numerical analysis and test destruction form

1)峰值状态时，模型塑性应变主要集中于榫卯接缝横向凸起根部及受拉侧边缘构件下部，并在接缝上部向榫卯板扩散分布，与试验中试件裂缝开展吻合。破坏时塑性应变加剧，且从分布情况看，接缝上部凸起位置塑性应变数值较小，中下部凸起部分较大，与试验结果一致。

2)数值分析准确地模拟出试件SPW- H相比试件SPW- 1破坏程度加大的现象，同时破坏状态时试件SPW- H数值模型墙角塑性应变数值较大，与试验中仅试件SPW- H墙体根部发生较大混凝土压溃的现象相吻合。

图5为峰值状态时墙体钢筋Mises应力分布云图。钢筋应力分布表现出明显的分区特征，主要分布于试件对角线上部以及墙体根部区域，两侧竖向钢筋达到屈服应力，水平分布钢筋基本未屈服，与试验钢筋应力情况吻合。

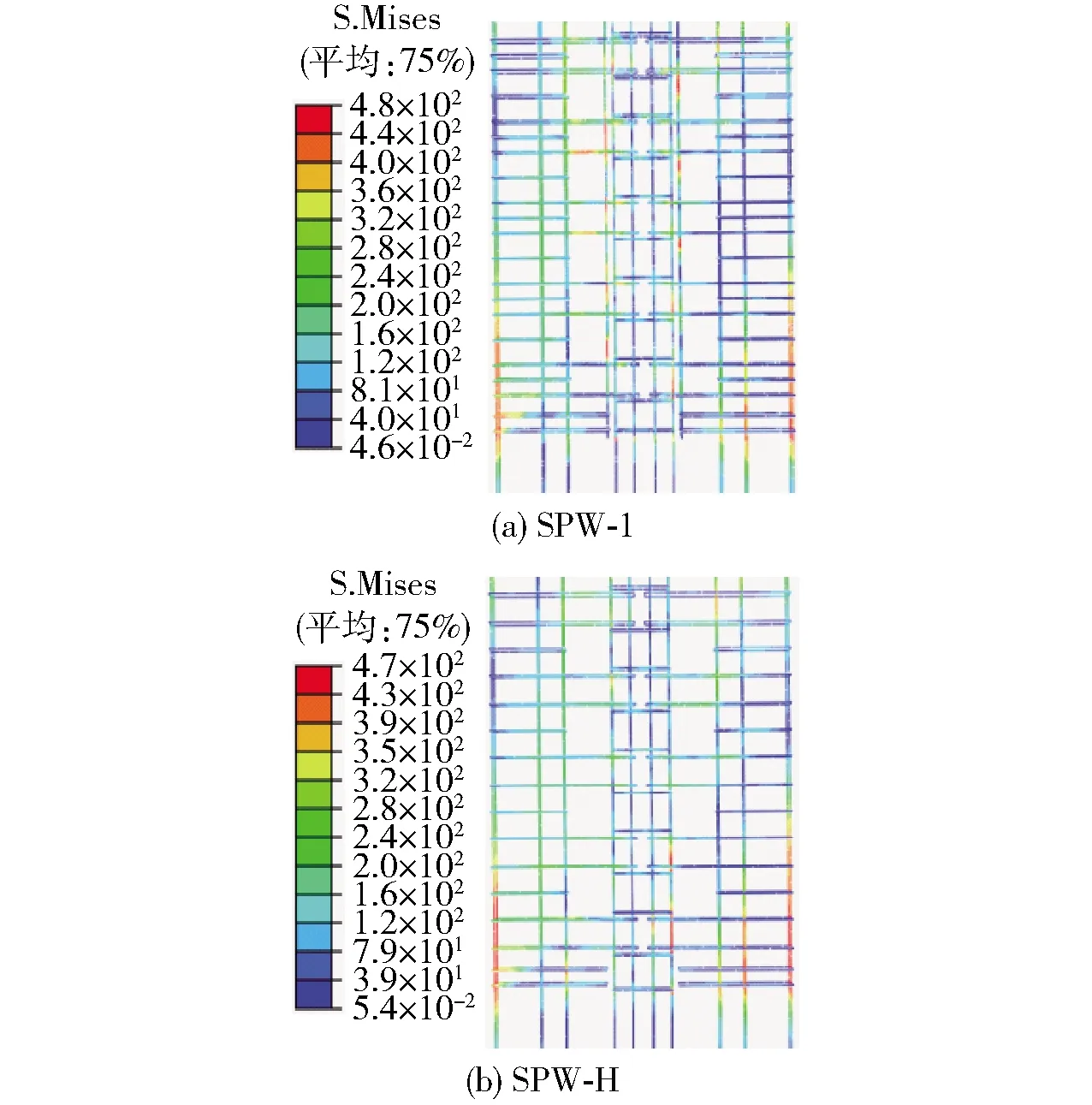
图5 钢筋Mises应力分布云图/MPaFig.5 Mises stress distribution of steel bar/MPa

3.2 骨架曲线及特征点对比

数值分析所得荷载- 位移曲线与试验骨架曲线对比如图6所示，试验结果与数值分析结果峰值状态特征对比见表3。数值分析所得荷载- 位移曲线与试验骨架曲线吻合，承载力以及下降段呈现基本一致的变化趋势，承载力误差在4%以内，数值模拟方法合理、可靠。

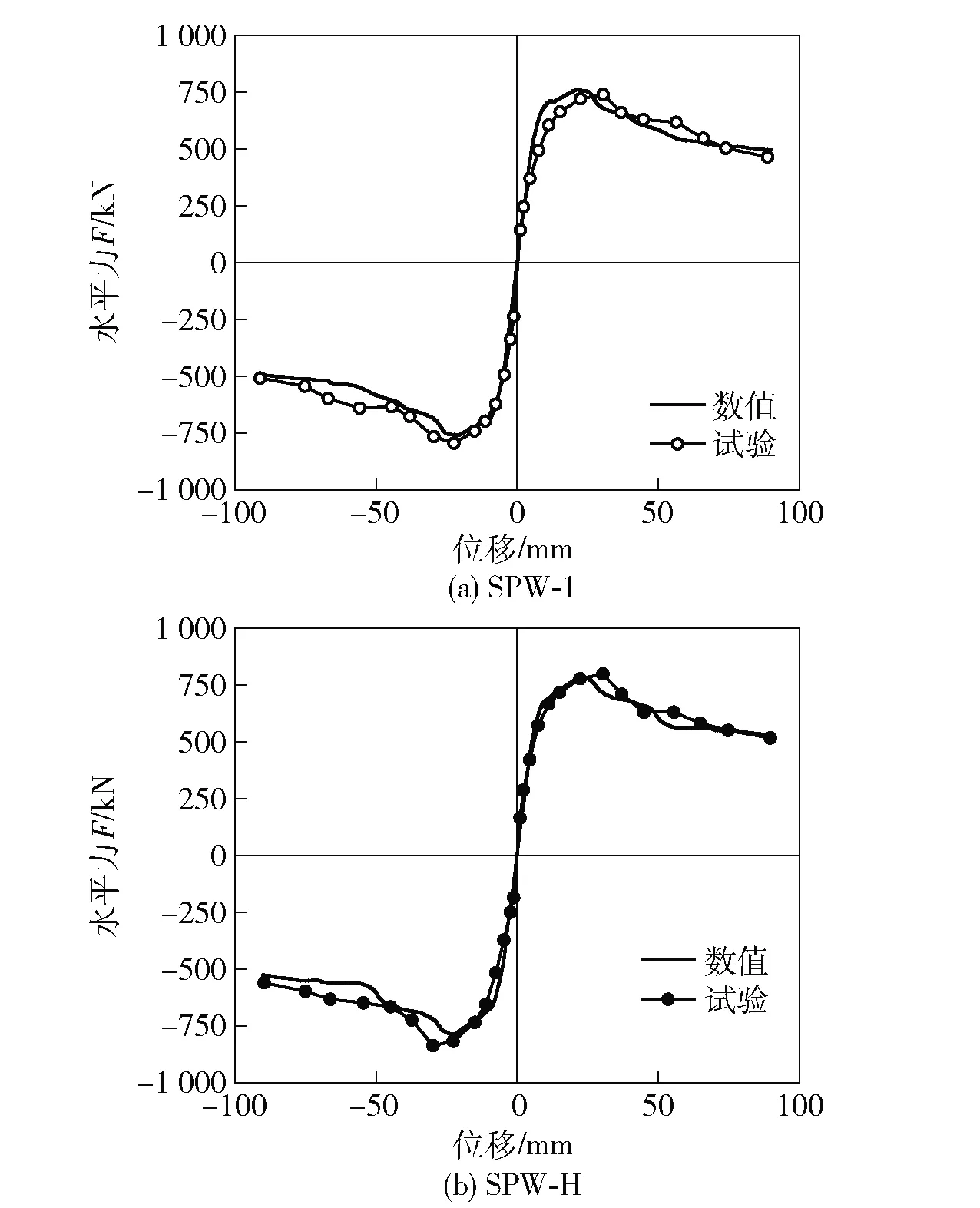
图6 荷载- 位移曲线对比Fig.6 Comparison of load-displacement curves

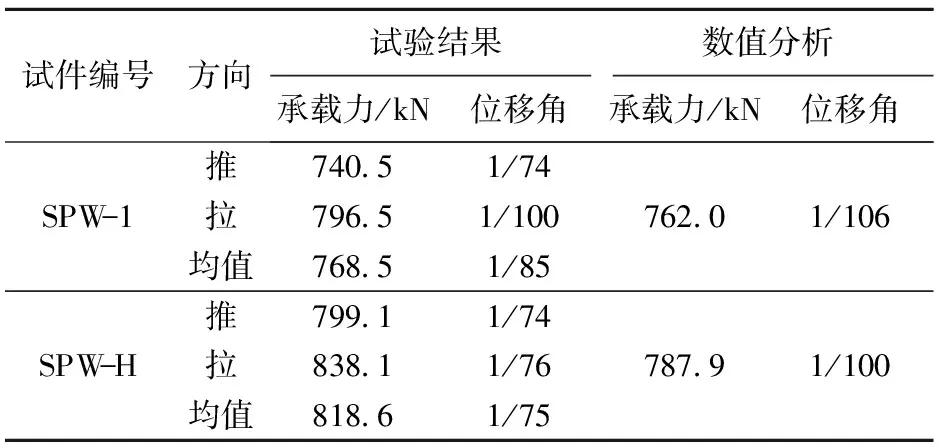
表3 试验结果与数值分析结果对比

4 参数扩展

4.1 构造尺寸

试验中试件SPW- 1与试件SPW- H纵向孔洞长边皆为130 mm，此时孔洞内缘与横向凹槽内侧平齐。为探究纵向孔洞尺寸对接缝连接性能的影响，建立了3个纵向孔洞长边分别为120 mm、150 mm及170 mm的有限元模型，其孔洞内缘分别伸出预制板10 mm、伸入预制板20 mm及40 mm，其余设计参数与试验模型SPW- 1相同。图7为不同纵向孔洞尺寸试件的荷载- 位移曲线，可以看出，四试件曲线弹性段斜率大致相同，纵向孔洞尺寸对榫卯剪力墙的初始刚度影响不大。当纵向孔洞长边由130 mm改为150 mm时，试件峰值承载力降低了3%，由150 mm改为170 mm时，承载力持平，故纵向孔洞内缘伸入预制板时，试件承载能力受影响较小；纵向孔洞尺寸由130 mm缩小到120 mm时，承载力下降了6%，纵向孔洞内缘伸出预制板时，试件承载能力降低。

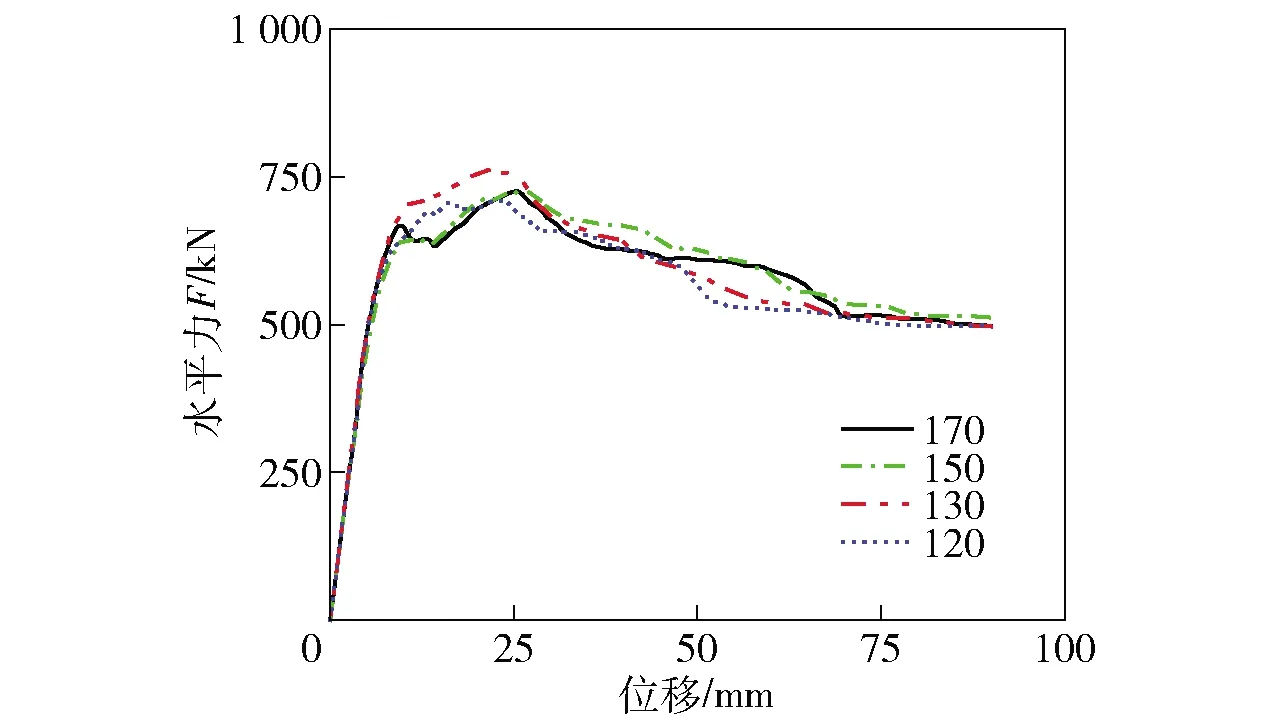
图7 不同纵向孔洞尺寸试件的荷载- 位移曲线Fig.7 Load-displacement curves of specimens with different longitudinal hole sizes

图8为各试件位移角为1/120时的塑性应变分布云图，可以看出，试件的破坏均集中于榫卯接缝凸起根部位置，且当纵向孔洞内缘与横向凹槽内侧平齐时(130 mm)，试件塑性应变较小，并集中于接缝处，预制墙板处较少塑性应变分布；当选取非平齐设计时，试件均出现塑性应变向墙板分布的现象，且塑性应变较大，同时在纵向孔洞尺寸较小时(120 mm)，接缝处塑性应变显著增大，产生此现象的原因在于试件采取非平齐设计时，其内作为竖向接缝处薄弱位置存在的新旧混凝土结合面总面积增加，使得接缝处破坏增大。综上所述，纵向孔洞内缘与横向凹槽内侧平齐为合理设计。

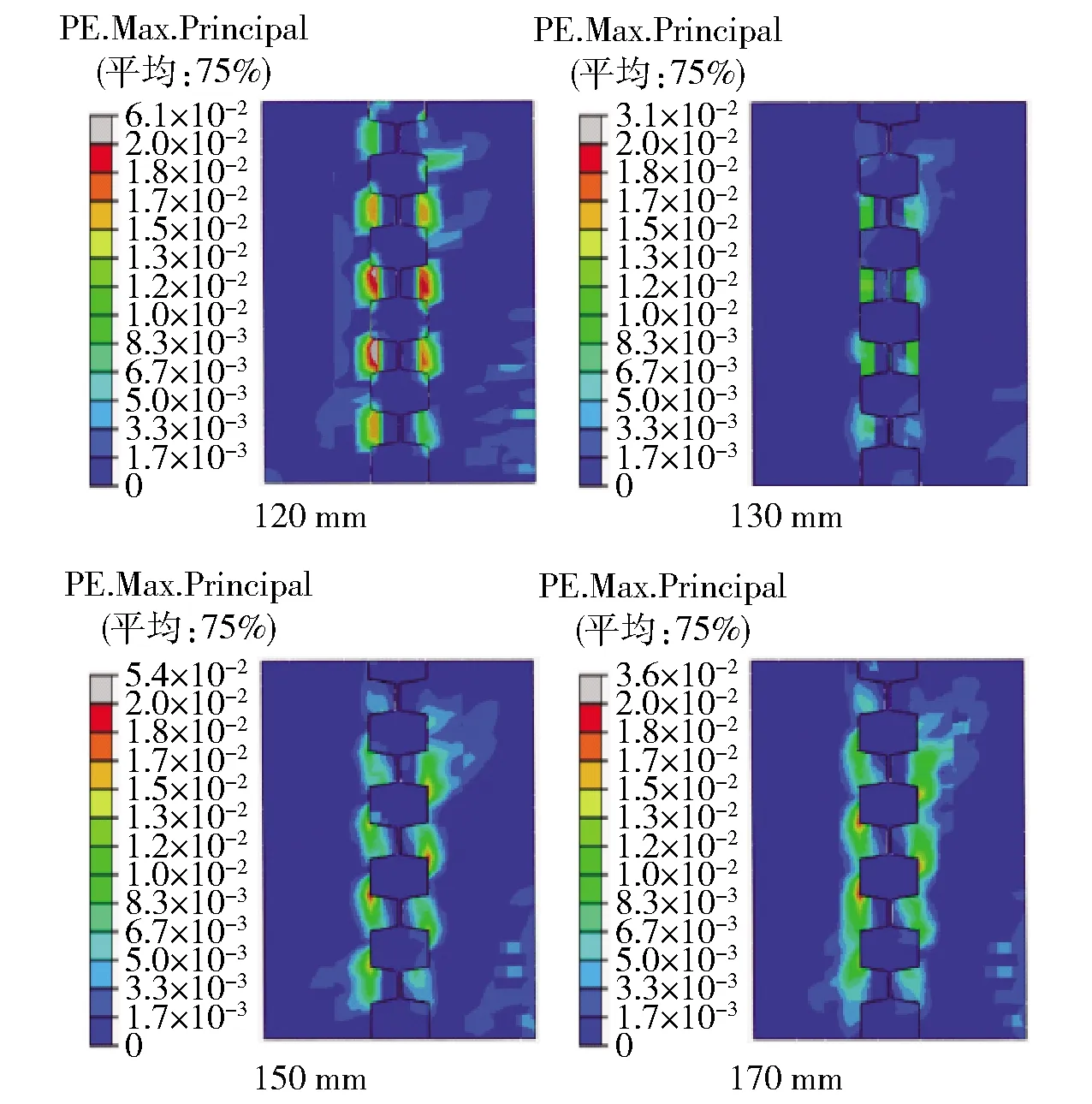
图8 不同纵向孔洞尺寸试件塑性应变分布云图Fig.8 Plastic strain distribution of specimens with different longitudinal hole sizes

4.2 水平分布钢筋

试验结果表明，水平分布钢筋配筋率的提升可少量提升试件峰值承载力，增大试件峰值位移角，对墙体的破坏形态影响不大。为进一步研究水平分布钢筋配筋率对榫卯剪力墙受力性能的影响，在确定板型为纵向孔洞内缘与横向凹槽内侧平齐的基础上，以试件SPW- 1为基准模型，建立了2片水平分布钢筋配筋率为0.89%及1.58%的有限元模型进行单调推覆分析，并与试件SPW- 1及SPW- H的模拟结果进行对比。

图9为模拟结果的荷载- 位移曲线，可以看出，水平分布钢筋配筋率提高对墙体初始刚度无影响，可提高试件峰值承载力及峰值位移角。图10为水平分布钢筋配筋率与试件变形能力的关系，随着水平分布钢筋配筋率的提高，剪力墙破坏位移及屈服位移随之增大，延性系数影响不大，基本保持在4.25左右。综上，提升水平分布钢筋配筋率对榫卯剪力墙受力性能影响不大，此是因为榫卯剪力墙为压弯破坏，原水平分布钢筋配置满足试件抗剪要求并具有一定的安全裕度。

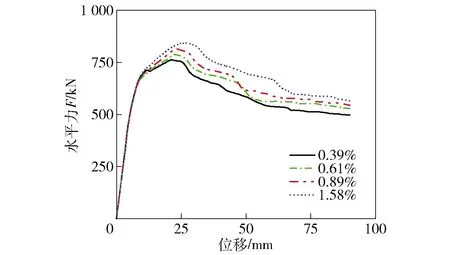
图9 不同水平分布钢筋配筋率试件荷载- 位移曲线Fig.9 Load-displacement curves of specimens with different horizontal reinforcement ratios

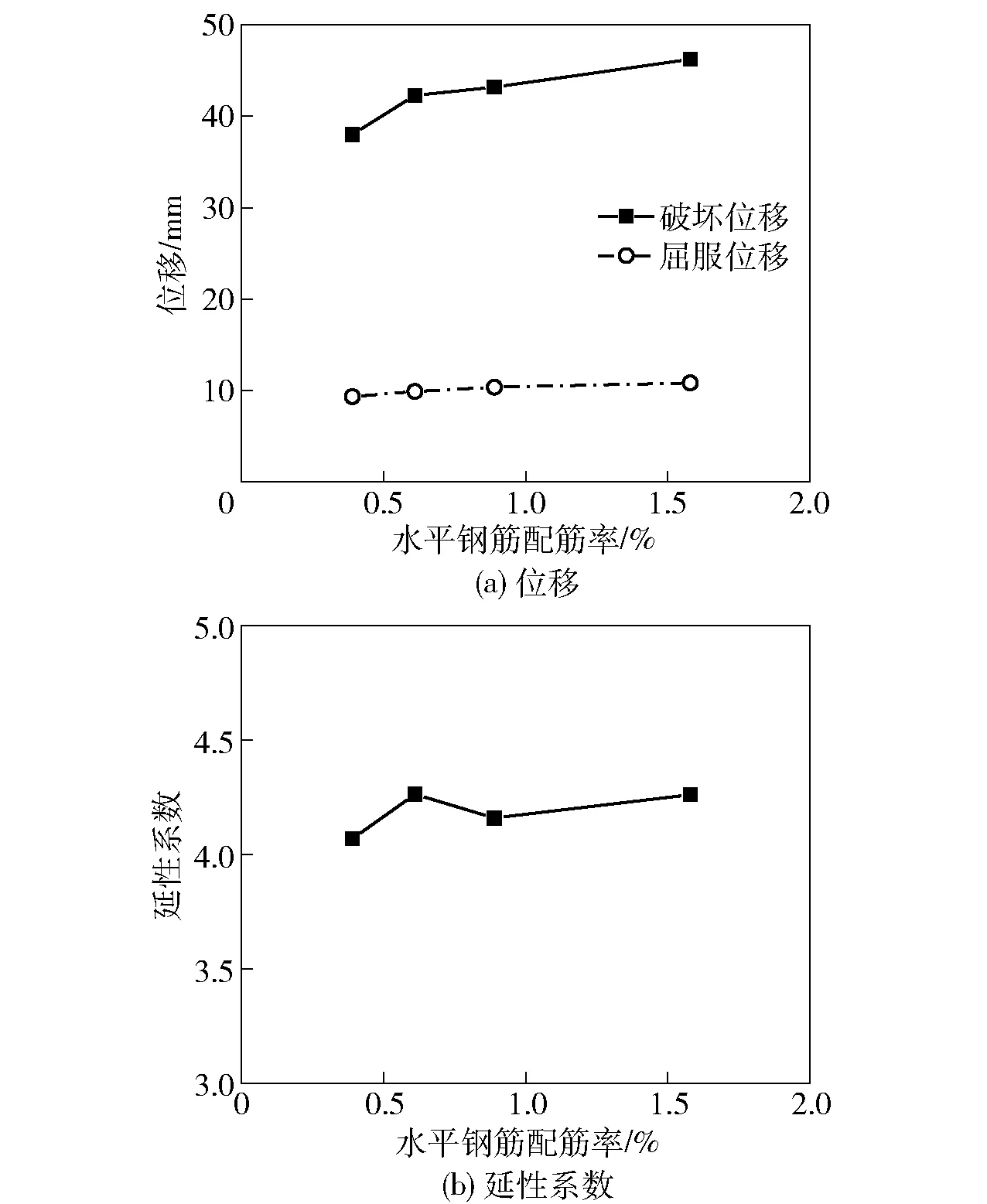
图10 变形能力影响曲线Fig.10 Influence curve of deformation capacity

4.3 轴压比

轴压比是影响结构性能的重要因素，轴压比增大，剪力墙承载力及刚度增大，但延性会降低[14-15]，合理的轴压比选用对剪力墙的抗震性能具有重要意义。图11为不同轴压比条件下试件数值分析结果提取的荷载- 位移曲线，可以看出，初始加载时，试件基本处于弹性阶段，不同试件曲线斜率大致相当，轴压比对初始刚度的影响较小；随着轴压比增大，试件达峰值荷载后，承载力下降显著加快，试件破坏提前，变形能力降低。

图11 不同轴压比下试件荷载- 位移曲线Fig.11 Load-displacement curves of specimens under different axial compression ratios

表4为各试件达屈服、峰值、破坏状态时对应荷载、位移角以及延性系数(μ=θu/θy)，可以看出，随着轴压比的增大，试件承载能力提高，轴压比为0.30的试件相比轴压比为0.10的试件峰值承载力提高了22%，但峰值位移角、破坏位移角均减小，延性降低，轴压比对试件屈服位移角影响较小，各试件达屈服状态时，位移角相当。