基于多目标的汽车前端框架拓扑优化

杨剑飞, 周超群，王建彬，李 飞

（1.安徽工程大学机械工程学院，安徽，芜湖 241000；2.芜湖恒信汽车内饰制造有限公司，安徽，芜湖 241000）

0 引言

汽车前端不但是车身外观造型的主要组成部分，也是汽车安全性能的重要保证。前端框架是汽车前端模块化和集成化安装平台的重要支撑，其结构优化对整车轻量化设计和操控性能提升至关重要。传统的汽车前端通过专门的骨架集成了100 多个散部件，不利于整车结构优化和操控性能提升。随着整车轻量化要求的提高，汽车前端的模块化和集成化趋势日益明显。前端框架作为前端模块各部件的安装和支撑平台，其结构和力学性能指标至关重要，也是汽车前端结构优化和轻量化设计的关键对象。

拓扑优化技术属于结构优化技术中的一种，可在给定的设计空间中找到最佳的材料分布以及结构的形状，从而在达到性能的要求下实现轻量化[1-2]。拓扑优化常用的方法有均匀化方法、各向正交惩罚材料密度法、变厚度法、拓扑函数描述方法等[3-5]。目前，常用的单目标拓扑优化主要针对连续体的研究对象，难以描述复杂的多工况场景[6-8]。研究人员采用加权组合将多目标问题转化为单目标问题。范文杰等以体积和频率作为约束，以承受扭转以及弯曲等多种载荷工况下对应的最小柔度作为目标函数，其扭转和弯曲的权重设为同等重要,将一阶频率和刚度进行多目标优化[9-10]。祝小元等利用Hyperworks 软件中的结构优化模块OptiStruc，采用多级容差序列算法对优化的过程进行分步处理，最终得到在多工况下的以柔度最小及震动频率最高结果[11]。刘林华等基于折衷规划法结合平均频率法建立了多目标拓扑优化的越野车车架数学模型，并通过优化得到了同时满足刚度和振动频率要求的车架拓扑结构[12-13]。

在多目标拓扑优化时，对其子工况下的权重比例选择是重要的。其子目标权重系数的选择方法有三种，其一是为不同目标函数分配权重，此方法是借助单目标函数求解方法来解决多目标问题。康元春等将多目标函数权重问题通过加权转化为单目标，则在各个目标之间进行协调权衡和折衷处理使各子目标均达到最优[14]。其二是子工况明显具有重要性或者有优先级的问题。胡启国等引用多级容差序列规划法，按照重要程度对静动态多优化目标进行分级处理，则避免了当子目标数量级不同时出现的载荷病态现象[15-16]。其三是适合于不同目标函数重要性的帕累托前沿计算问题。唐华平等利用Pareto 解集思想很好地兼顾多个优化目标间的均衡[17-18]。

本研究将原始汽车前端框架结构处的筋进行3D 网格填充，重新建立汽车前端的有限元模型，作为基础结构进行拓扑优化。由于动态模态特性需要考虑子目标函数的相对重要性，则通过层次分析法将前三阶模态固有频率进行加权[19]。对于静态特性权重系数的选择来说，由于子目标数量过多难以准确的判断相对重要性，则通过灰色综合关联法将四种不同工况下的子目标进行权重分配[20]。最后通过折衷规划法[21]将动静态分配的权重进行归一化处理，将公式进行拟合，通过Hyperworks 软件进行动静态多目标拓扑优化。根据优化后的结果对填充实体进行改进设计，对比原始结构的分析结果表明，改进后的汽车前端的整体刚度、强度性能和固有频率均有所提高且质量减轻，轻量化效果明显。

1 初始有限元模型建立与静态特性分析

1.1 有限元模型建立

汽车前端框架包括上下两个梁、左右两个立柱，上梁连接的两个固定钣金，梁与臂里面开设的加强筋。通过Hypermesh 对该模型进行抽取中面以及网格的划分。其非钣金区的设计材料为PP-LGF30（30%长玻纤增强，高刚性高强度，耐疲劳），其属性为弹性模量4800 Mpa，泊松比为0.34，密度为1.12 g/cm3,屈服应力为78 Mpa。钣金区的弹性模量为210 Gpa,泊松比为0.3，密度为7.85 g/cm3。抽取其中面后附属在其梁上面的筋所采用的厚度为2 mm，壁厚为2.5 mm，钣金的厚度为1.2 mm。网格的划分采用的是四面体网格的方法，利用Rbe2单元将上梁与钣金连接起来，共生成的单元数量为129050 个，原汽车前端框架质量为3.55 kg。建立起的有限元模型如图1 所示。

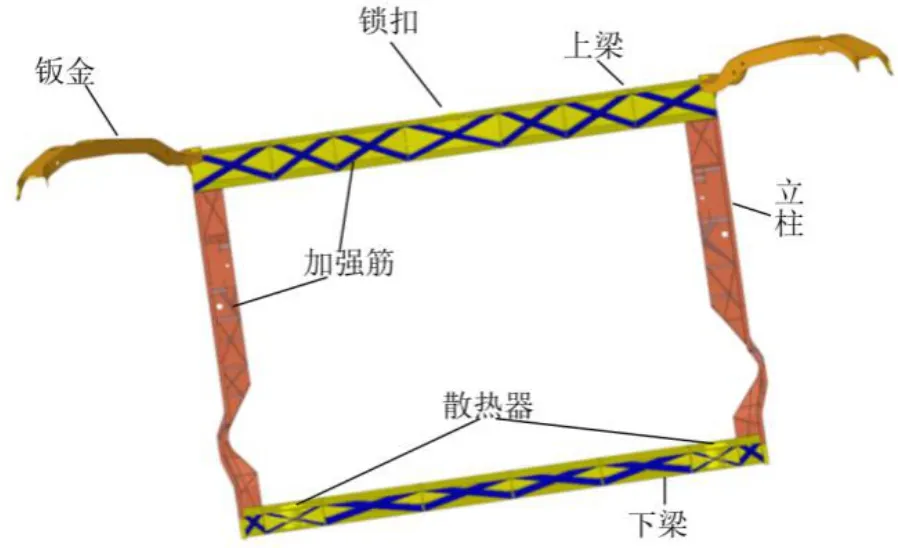
图1 汽车前端框架有限元模型Fig.1 Finite element model of automobile front-end frame

1.2 静力学分析与模态分析

基于对汽车前端框架一些典型的工况进行分析，结合重要部件处的受力分析所设置四种工况，受力点在锁扣处和散热器处。针对施加力边界条件设计如下：分别设置锁扣处+X 方向150N,-Z 方向300N，散热器处+Z 方向67.5N，+X 方向125N。针对约束边界条件，通过Reb2 在两个立柱处建立约束，此处是与车身防撞梁处连接，所以连接点处约束六个自由度方向，另两个钣金处也要建立约束，此处是与车身钣金处相连接，因此在连接处也需约束六个方向的自由度方向。针对这四种典型工况载荷，分别对该汽车前端进行静力学分析，以及在自由状态下，对该汽车前端进行模态分析，静力学分析结果如表1，模态分析结果如表2。

表1 初始汽车前端刚度和强度分析结果Table 1 Initial automotive front stiffness and strength analysis results

由表1 结果表明，汽车前端在锁扣Z 向处出现的最大变形量为2.69 mm 且最大应力表现为19.57 Mpa，明显其刚度以及强度过低，性能较差，有必要对该汽车前端进行优化设计改进。为了提高其整体的刚度性能可结合四个工况来对其优化改进。为减小汽车前端框架在某种工况下的整体变形，采用结构整体柔度为优化目标。柔度作为力学中的一个概念，表示为在力的作用下可以反应弹性变形的能力，柔度实为刚度的倒数[22]。

由表2 结果表明，在1 阶时固有频率为30.92 Hz，而土路和城市道路的不平度波长在0.77～6.3 m，汽车常用车速一般在80 km/h，根据在不同波长上的路面行驶的车辆速度和激励频率的关系计算[23]：

式中，f为激励频率；v为汽车行驶速度；λ为路面不平度波长。

计算出的路面激励频率范围为3.53～28.86 Hz，而一阶模态的定义是物体固有频率与外在的激励频率出现等值时的值，所以从表2 中可以看出第一阶时的固有频率接近路面的外在激励，有可能会发生共振。发生共振一般情况下是有危害，会引起机械和结构上很大的变形，因此需要提高一阶乃至低阶的固有频率。

2 综合目标拓扑优化方法

2.1 灰色综合关联法

灰色系统理论是由我国控制专家邓聚龙教授在20 世纪80 年代初创立的，在其关联分析中，每一种类的数据值的大小所反应的实际意义可能不同，但是各个数据的数值其关联度在实际意义上也有一定的关联。因此，将多个这类需要关联比较的序列作为关联序列Xi，将参考序列作为被比较的序列Xj，基于灰色关联分析理论将关联序列与被关联序列进行分析计算，得出关联度。

基于灰色综合关联法，将各个工况所进行的单目标优化柔度结果的数值列为关联序列记为Xi，然后在各个工况单目标优化的柔度数值中挑选该工况中最优解作为被比较的序列记为Xj。设四个工况所分析的数据形成以下矩阵[24]：

2.2 层次分析法

由于模态分析中一阶模态较其他模态更加重要，考虑到单目标优化模态时各阶模态具有明显的重要性，既不能忽略高阶模态的作用，也不能夸大低阶模态的作用，所以将单目标优化中的前三阶模态进行加权拟合。对于这种需要考虑目标函数的相对重要性问题，所采用的是运筹学中的层次分析法[26]。

表3 判断矩阵中因素的重要性比对表Table 3 Importance comparison table of factors in the judgment matrix

式中，0.1 为判断界值，若CR小于0.1 则表明该判断矩阵通过一致性指标，否则不通过则需要重新构造判断矩阵。平均随机一致性指标RI标准值如表4 所示。

表4 随机一致性参考标准值Table 4 Random consistency reference standard values

2.3 折衷规划法

通过上述分析，灰色综合关联法是用来计算四个工况的权重比例，层次分析法是用来求不同阶模态之间的权重比例。汽车前端在拓扑优化阶段考虑静态柔度特性以及动态频率特性，因此根据折衷规划法将多目标优化问题转化为单目标优化问题，利用带权重的综合目标函数[28]：

综上所述，基于折衷规划法、灰色综合关联法与层次分析法相结合的多目标拓扑优化流程如图2所示。

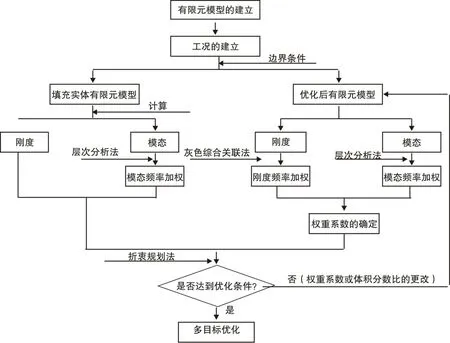
图2 多目标优化流程图Fig.2 Flow chart of multi-objective optimization

3 汽车前端拓扑优化

3.1 单目标拓扑优化

在Hyperworks 中对初始结构的上下梁进行填充，上梁与下梁是作为优化的设计区域，所以在优化之前将上梁与下梁进行实体填充，同时保留立柱的原有位置与空间，基于此基础上建立有限元模型。材料方面与之前相同，设计区域材料为弹性模量4800 Mpa,泊松比为0.34，密度为1.12 g/cm3，屈服应力为78 Mpa，如图3 所示。

图3 实体填充有限元模型Fig.3 Solid filling finite element model

在四个工况点受力处进行单目标优化和单目标前三阶模态优化，优化的目标是降低汽车前端在各个工况处的柔度值和提高汽车前端的固有频率值，优化所设计的要求约束为不超过体积分数的上限百分之三十。在进行单目标优时，优化中设置了最小成员尺寸以及最大尺寸。由于模型在划分网格时将平均网格尺寸设置为3 mm，根据最小成员尺寸一般设计为单元尺寸的2-3 倍而最大成员尺寸一般设计为3-4 倍，所以将最小成员尺寸及最大成员尺寸分别设计为6 mm 和12 mm。优化的结果如图4 所示。

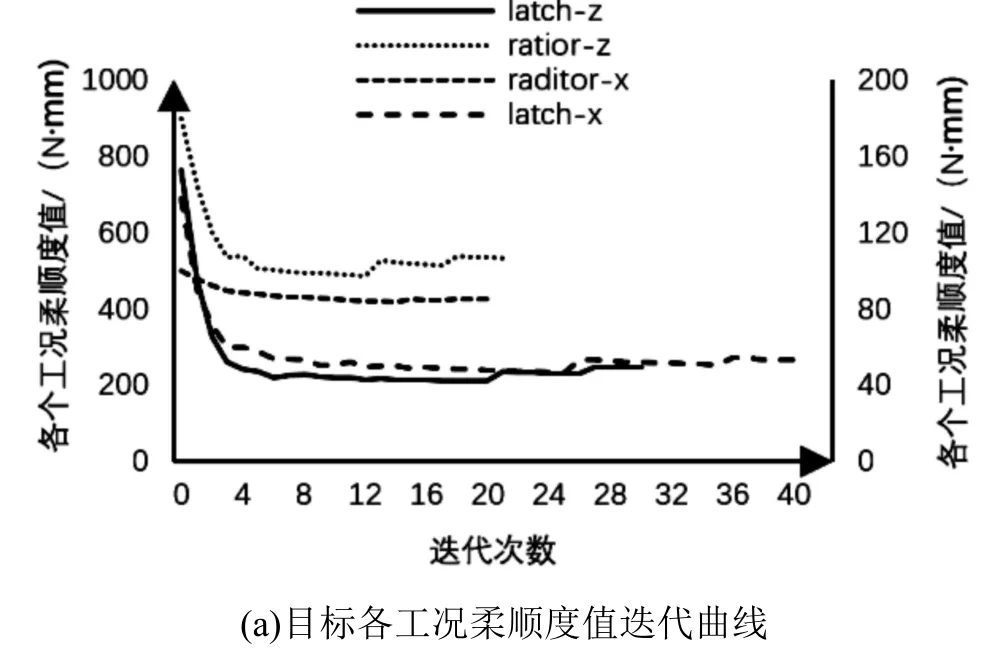
图4 单目标优化结果Fig.4 Single objective optimization results

图4(a)所示latch-z、latch-x、ratior-z、ratior-x所代表的是锁扣Z 向、锁扣X 向、散热器Z 向、散热器X 向的单目标优化结果，(b)所示moda11、modal2、modal3 所代表的是第一阶模态、第二阶模态、第三阶模态。由于Optistruct 软件所使用的是SIMP 插值的方法，并且设置了最小成员尺寸且该优化为壳单元，故该软件所定义的初始惩罚系数为3，优化中后面两个阶段都逐渐增加到4。因此计算机在设计阶段会重新进入一个新的阶段，所表现的形式如图4 所示有三段的迭代过程。

3.2 多目标拓扑优化

由上述分析可知，采用折衷规划法时需将各工况柔度及前三阶模态的各个权重比计算出，各工况柔度采用的方法是灰色综合关联法而前三阶模态采用的是层次分析法。对与各工况柔度而言，选择柔度单目标优化中的最小值作为优化结果值设其为被关联序，将各工况的优化结果形成的序列作为关联序，取分辨系数ρ为0.5，采用灰色综合关联法计算，其关联序与被关联序如表5 所示。

表5 关联序列与被关联序列Table 5 Correlation sequence and associated sequence

将关联序列与被关联序列的数据经过灰色关联法计算，经无量纲后通过式（5）计算可得其关联系数θn(k) ，则关联序权重经归一化后可知四工况下的权重比如表6 所示。

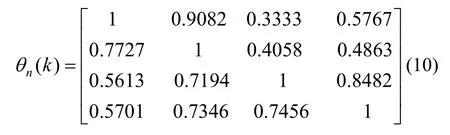
表6 四工况单目标优化权重比Table 6 Single objective optimization weight ratio in four working conditions

对于固有频率来说计算权重采用的是层次分析法，前三阶固有频率根据其两两之间的重要程度对比，参考表3 可构造出的判断矩阵Aij。

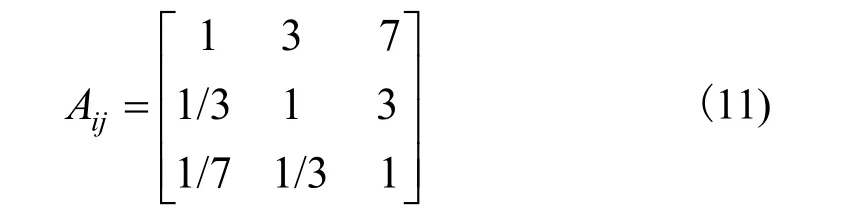
根据矩阵求其特征值得到最大特征值为3.007，由于所拟合的是单目标固有频率的前三阶模态,所以n取为3，通过表4 可知RI=0.58，根据式（8）可计算出CI=0.0035，在根据式（9）可计算出CR=0.006＜0.1，判定所构造的矩阵一致性是可以接受的。将判断矩阵Aij归一化得到Bij:

归一化后的矩阵Bij进行行向量相加并进行归一化处理后得到权重第一阶模态、第二阶模态、第三阶模态的权重比分别为0.67、0.24、0.09。本研究对汽车前端多目标静动态优化，并且结合实际要求在柔度和固有频率的权重比取为0.6、0.4。

在Hyperwork 中的optistruct 模块下dequations里输入上述基于折衷规划法计算出的公式进行多目标拓扑优化分析，综合目标为最小函数值结果，约束为不超过体积分数上限的0.35，经过计算机计算43 次迭代后收敛，结果如图5-7。

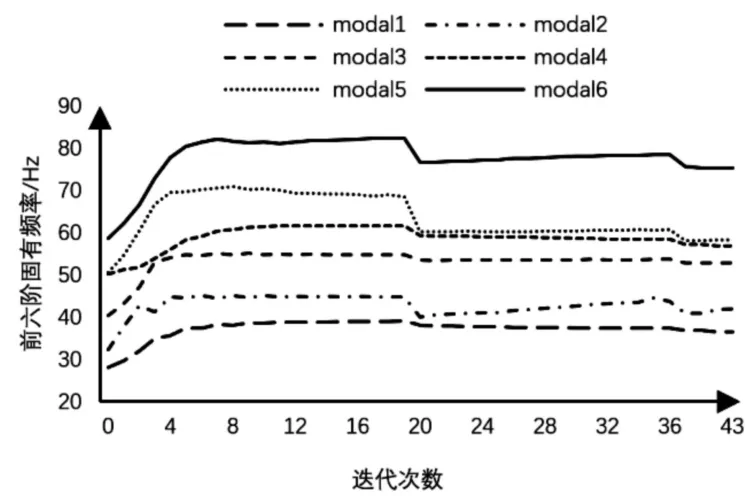
图5 多目标固有频率迭代曲线Fig.5 Multi-target natural frequency iteration curve

多目标优化迭代结果表明，综合目标函数迭代过程中，由于惩罚系数3，到后两个阶段4 的变化，虽经历三个阶段，最终迭代的结果依然为降低。前六阶频率均有提升且震荡现象不明显，整体上升趋势较平坦。柔顺度值中散热器Z 方向柔度虽有小幅度上涨，但占整体的比例不大。汽车前端经过多目标优化后的材料密度分布云图如图8 所示。

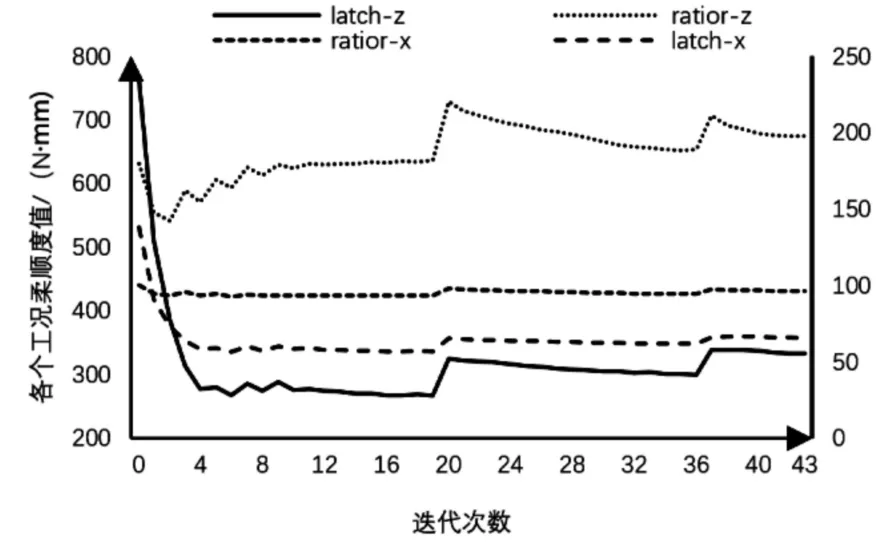
图6 多目标各工况柔顺度值迭代曲线Fig.6 Iterative curve of compliance values in various working conditions of multiple targets

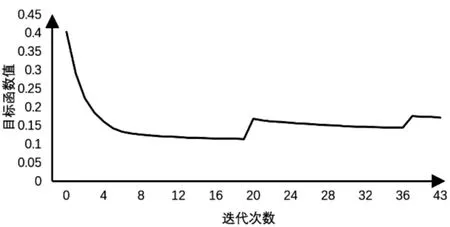
图7 综合目标函数迭代曲线Fig.7 Iteration curve of synthetic objective function

图8 多目标拓扑优化结果Fig.8 Results of multi-objective topology optimization

OptiStruct 拓扑优化中的材料模式使用的是SIMP 方法，即是单元密度与材料弹性模量之间的一种函数关系，取值在0～1 之间连续取值，若优化后求解单元密度越靠近1 表示该区域越重要不可去除，若单元密度越靠近0 则表示该区域越不重要可去除[30]。由HyperView 中结果可知，在上下梁中间加筋可根据该结果图进行设计，然后再结合工程需要考虑该部分是加筋还是挖空。

3.3 汽车前端上下梁改进与分析

以多目标分析的材料密度分布云图作为主要设计改进依据，然后结合工程需要进行改进设计，目的是使得汽车前端在满足各性能要求下，质量也相应地降低，以满足轻量化的需求。结合产品工艺性需求，由于该汽车前端是塑料件，要进行注塑环节则需在下梁里加一些薄筋，目的是在注塑期间保证下梁不变形。基于原结构改进设计后的汽车前端框架如图9 所示。

图9 汽车前端改进后结构Fig.9 Improved structure of automobile front end

改进后的汽车前端结构的质量为3.32 kg,相比原始汽车前端结构在质量上减轻了7%。该质量百分比减轻是包含非设计区域的，因此减轻比重效果良好，符合轻量化要求。对改进后的汽车前端框架再次进行静力学分析与模态分析，分析对比结果如表7、表8 所示。

由表7 可知，前三阶模态提高，而前三阶模态是参与多目标优化的对象，动态特性显著提高。

表7 汽车前端改进前后的前6 阶固有频率对比Table 7 Comparison of natural frequencies of the first 6 orders before and after automobile front end improvement

由表8 可知，改进后的汽车前端框架在锁扣Z向、锁扣X 向两个工况下的变形量和应变有大幅度的降低，而下梁由于刚度相比上梁小，即在多目标优化时下梁会先出现模态优化，这样则导致在散热器Z 向、散热器X 向最大变形量和应变有小幅度的上涨。但对整体比例来说，最大的变形由2.690 降低到2.107，最大的应力由19.57 降到12.84，即对于整体而言，刚度性能和强度性能提高。

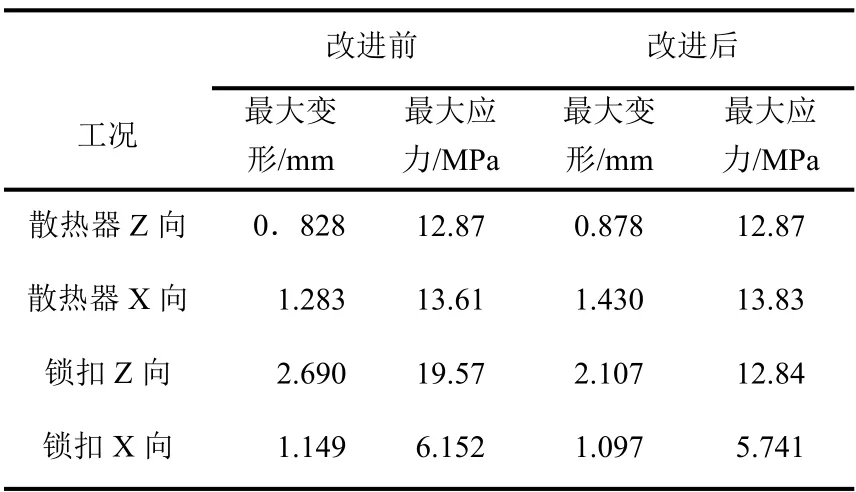
表8 汽车前端改进前后刚度和强度特性对比Table 8 Comparison of stiffness and strength characteristics before and after improvement of automobile front end

4 结论

1）基于带权重的折衷规划法建立起了以多工况下静态柔度和动态固有频率的综合目标函数，通过灰色关联法以及层次分析法两种侧重点不同的方法来计算子目标的权重系数，这样则在子目标权重的选择上更加合理，为工程中多目标拓扑优化设计提供了一种有效解决方法。

2）以某汽车前端框架为实例，运用该方法进行汽车前端的多目标拓扑优化。在多工况下的静态柔度权重分配上选择灰色关联法，由于低阶模态较高阶模态重要程度相对高点，则动态特性固有频率的权重分配采用层次分析法，将分配权重归一化后得到目标函数。优化后结果表明，该目标函数收敛速度更快，优化效果更好，并且在满足轻量化的要求下，刚度性能、强度性能以及动态特性均有所提高。

3）由于实验成本及条件的限制，本研究主要基于有限元仿真分析，并未对优化结果进行实车试验验证，后续需进一步深入研究，以确保优化结果的可靠性。