非均匀海水中水平电偶极子在空气中产生的电磁场

任英达， 王宏磊， 杨坤德

(1.西北工业大学 航海学院，陕西 西安 710072； 2.海洋声学信息感知工业和信息化部重点实验室(西北工业大学)，陕西 西安 710072)

由于声波在海水中具有较小的衰减，因此水声技术目前被广泛应用于水下探测和水下通信领域[1-3]。但水下声传播的速度低、延时大，特别是在浅海环境中，声学系统面临诸多挑战，如多径传播、来自空气界面和海底的回波、人造噪声等以及靠近海岸的复杂传播路径。此外，声波无法突破海洋界面直接传播，这也限制了水声技术的发展和应用。水下光通信的传输速率很高，但是光损耗很大[4-5]，其对海水的清洁度要求也很高。同时只有在收发设备都精确对准的情况下才能正常通信，因此实际动态海洋环境也限制了水下光通信技术的发展。电磁波在海水中传播时会产生较大的衰减，频率越高衰减越大。但同时水下电磁波传播速度快、传输延迟低、不受海洋环境噪声影响，尤其是能轻易穿透海水界面传播。近年来，电磁波在海水中传播时的诸多优点吸引了越来越多的中外研究人员的关注[6-7]，同时水下电磁场的相关应用也越来越广泛[8]。

对海水中电磁波传播的研究实际上是对分层导电媒质中电磁波传播的研究。长期以来，针对海洋分层媒质中电磁波传播的建模和特性分析，开展了多项理论研究。通常人们仅考虑空气-海水-海底3层介质，分析其中电磁波的传播。Wang等[9]基于3层媒质模型，研究了海水中的偶极子在空气中的辐射场，并采用快速傅里叶变换法将电磁场表达式中Sommerfeld形式的积分展开成离散傅里叶级数的形式，而后采用数值方法求解；该方法能够快速、准确地得到几个波长以内的结果。Qu等[10]基于3层媒质模型研究了浅海环境中上下界面对海水中电磁波传播的影响。然而传统的3层模型并没有考虑真实海水的非均匀性。真实海水中随深度变化的电导率对水下电磁波传播，尤其是跨海-空界面传播会产生较大的影响。

本文针对海水电导率随深度变化时，水下电偶极子在空气中辐射的场展开研究。在传统空气-海水-海底3层模型的基础上，将海水视为多层媒质，基于直接全局矩阵对海水中水平电偶极子在空气中产生的电磁场进行建模计算。并与广义反射矩阵计算得到电磁场分量进行了比较分析。

1 海水电导率对电磁波传播的影响

海水作为一种导电媒质，它的传播常数与波矢量的关联方程式[11]为：

(1)

式中：εe=εs-jσs/ω为海水中的复介电常数；εs=εrε0；σs为海水中的电导率；μs为磁导率；εr为相对介电常数。由γ=α+jβ与式(1)可以得出：

(2)

(3)

式中：α为导电媒质的衰减常数，表示电磁波沿传播方向衰减快慢的程度物理量；β称为相位常数，表示电磁波在传播过程中相位变化的物理量。由于σ/ωε≫1，所以可以认为海水为良导体，由此也可以将式(2)和式(3)进行近似简化得出：

(4)

PL=-20lg(e-αz)

(5)

由式(5)可以看出无限大海水中电磁波振幅随传播距离的增加而呈指数衰减。衰减速度的快慢与衰减常数α的大小有着直接的关系。衰减常数越大衰减速率就越快，反之则衰减速率变慢。而电导率与衰减常数正相关，电导率的大小将直接影响电磁波在海水中传播时的衰减。

实际分层海洋环境下，电磁波跨界面传播时虽然不再满足指数衰减的规律，但电导率依然对电磁波的传播具有较大的影响。

2 传播模型的建立与求解

2.1 电磁波跨海—空界面传播模型

通常，海水中的辐射源在空气中产生电磁场时的3层模型结构[12]如图1所示(这里以水平电偶极子为例)，其中各层媒质的电磁参数如表1所示。

图1 电磁波跨海—空界面传播的基本模型Fig.1 Basic model of electromagnetic wave propagation across sea-air interface

表1 图1中不同媒质中电磁参数Table 1 Electromagnetic parameters in different media in Fig.1

实际上，由于海水并非空间均匀媒质，其电磁参数会随时间、空间变化，这点在前期的实验中也有所发现。这些参数的变化，尤其是电导率，会影响海水中及跨界面电磁波的传播。由于海水中电导率随深度变化尤为明显，如图2所示，根据不同深度电导率变化，可以将变电导率的海水分为多层。这样，模型才更加符合实际海洋环境，得到的电磁场计算结果和传播特性分析才更加准确。

图2 变电导率海水中电磁波跨海—空界面传播模型Fig.2 Model of electromagnetic wave propagation across sea-air interface in seawater with variable conductivity

2.2 传播模型的求解

当电偶极子位于多层媒质中时，可以将其在媒质中产生的辐射场看作许多TE和TM波分量的线性叠加。设定所有分层区域中的介质都是各向同性的，其中偶极子天线位于第m层海水中，将柱坐标原点设置在偶极子的中心位置，则模型中任一接收点处电磁场的坐标为(ρ,φ,z)，其各分量强度计算公式为[13]：

(6)

(7)

当分层有N层时，根据介质交界处的边界条件上要求的切向电场分量在所有ρ和φ处连续可以得到4(N-1)个方程，由于没有波来自无限远处，所以未知量个数也是4(N-1)。选取Al、Bl分量，根据相邻两层之间电磁场分量幅度系数的递推关系式，使用矩阵形式表示并简化为：

(8)

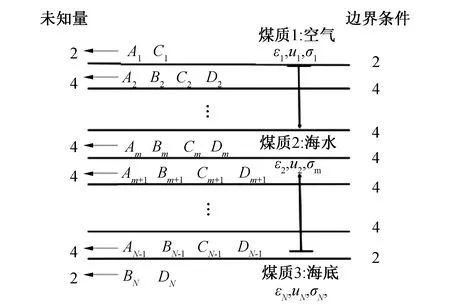
图3 多层模型中各参数分布Fig.3 Parameter distribution in multi-layer model

2.2.1 广义反射矩阵

通常，根据式(8)中相邻层幅度系数计算公式，可以逐层计算得到各层的幅度系数[14]:

(9)

由于水平电偶极子在第m层中，所以m层中电磁波的幅度系数还与电偶极子的激励幅度和结构相关，因此第m层中幅度系数应为：

(10)

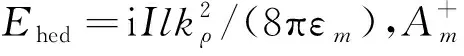
(11)

2.2.2 直接全局矩阵

直接全局矩阵多用于声场研究中多层传播媒质时对每层介质的声反射系数进行求解[15-16]，其主要原理是：根据相邻层之间的边界条件，构造矩阵将其结合起来组成方程组，对方程组进行求解后得到反射系数。这样保证了数值计算的稳定性，避免逐层误差传递。

由于界面处电场切向分量相等，相邻2层幅度系数之间关系如式(12)。其中，当分层厚度比较大并且所有层共用一个原点时，直接全局矩阵中的系数相差几个数量级。这将直接导致求解矩阵的奇异。但是通过将层的上界面作为下行波的原点，层的下界面作为上行波的原点，就确保了所有指数在介质层中都为负。且相互之间相差较小，避免了矩阵奇异的产生。

(12)

式中：

(13)

将(12)式和(13)式联立即可得到一个全局矩阵。求解后得到各层的幅度系数。在这期间也会产生一定计算误差η，其中空气中电磁场幅值系数为：

(14)

式中A1、B1为真实的幅度系数。对比式(11)与式(14)，直接全局矩阵计算得到幅值系数的误差相对较小，且不随海水分层累积传递。

3 仿真与结果分析

利用直接全局矩阵的方法，本文对真实海洋环境参数下水平电偶极子在空气中产生的电磁场进行仿真计算，其中设定海水中水平电偶极子的电偶极矩为1 Am，频率为15 kHz，发射深度15 m，仿真中空气接收高度20 m、接收角度均为φ=45°。

3.1 非均匀电导率对电磁波跨海—空界面传播的影响

图4中，海水垂直深度上的电导率为2018年夏季在南海某站位使用conductivity-temperature-depth system(CTD)实测数据。其中，在整个深度范围内，该站位海水电导率并非一个恒定值。在10 m深度范围内电导率基本不变，超过10 m后基本保持为负梯度变化，在30 m左右时再次出现拐点。其实测最大电导率为5.59 S/m，最小电导率为4.93 S/m。

根据不同深度的电导率将海水进行分层，并使用直接全局矩阵求解得到多层介质下海水中水平电偶极子在空气中产生电磁场分量如图5所示。除此之外，图5还给出了假设海水电导率恒定为4.93 S/m和5.59 S/m时的结果。经比较可以看出：当海水电导率非恒定时，得到的电磁场分量强度介于海水电导率恒定为最大和最小值时得到电磁场强度之间，与两者最大相差4.8 dB。由于本站位10 m深度范围内电导率基本保持为5.59 S/m，所以计算结果与恒定时近似。

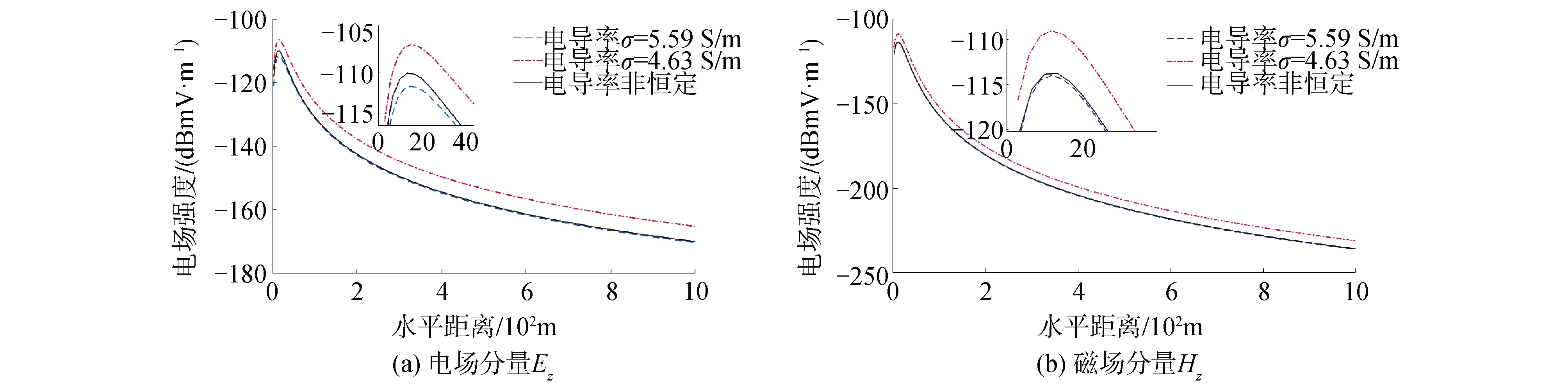
图5 空气中的电磁场分量强度Fig.5 The electromagnetic field components in the air

3.2 直接全局矩阵与广义反射矩阵对比

在2.2.1节中，分析了广义反射矩阵在计算多层导电媒质中电磁场时存在误差传递的现象，本节将通过仿真进行验证。

根据电导率变化，将海水分别设置为5层和10层，同时使用广义反射矩阵和直接全局矩阵对分层海水情况下电磁波跨海—空界面传播模型进行仿真。通过对图6中仿真结果对比，可以发现使用广义反射矩阵计算得到的电场分量在5层时与直接全局矩阵计算得到结果相近，但当层数升高到10层时电场分量曲线之间差距变大。这说明广义反射矩阵计算方法的确会随着介质分层数量的增加而误差增大。

图6 直接全局矩阵和广义反射矩阵计算得到的电磁场分量Fig.6 The electromagnetic field components in the air obtained by direct global matrix and generalized reflection matrix

为了进一步说明直接全局矩阵相比广义反射矩阵计算时的稳健性，对电磁场分量中的幅度系数B1随积分变量kρ的变化曲线画出如图7。理论上来说，由于本文给出的传播模型中空气为无限大上半空间，幅度系数B1=0。从图7中可以看出，直接全局矩阵得到的B1在所有kρ处都为0，与理论值相符；但广义反射矩阵得到B1不全为0，而且随着层数的增加，B1也在变大即误差也在变大。所以使用广义反射矩阵计算得到幅度系数相对于直接全局矩阵有较大误差。

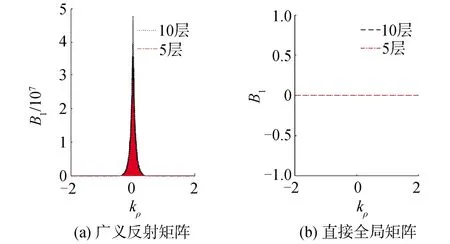
图7 电磁场分量的幅度系数B1变化曲线Fig.7 The amplitude coefficient B1 of electromagnetic field

4 结论

1)本文建立了垂直深度上电导率非均匀的海水中电磁波跨海—空界面传播模型，提出了基于直接全局矩阵的多层媒质中电磁波传播求解方法。并对变电导率海水中水平电偶极子在空气中产生的电磁场进行了建模和分析。结果表明，垂直深度海水电导率的非均匀性将对水下电磁波跨海—空界面传播带来影响，因此在理论建模过程中，需要将海水视为多层导电媒质。

2)文中定性对比了广义反射矩阵和直接全局矩阵的求解误差，分析了多层媒质中广义反射矩阵的误差累积过程。通过仿真获得了不同分层数量下电磁场强度和幅度系数，对比发现了采用直接全局矩阵求解多层媒质中电磁波传播将比广义反射矩阵更加准确和稳健。

3)文中提出的求解模型和方法对于利用电磁波实现水下目标探测和水下数据无线传输具有重要的理论价值，该模型和方法还可以应用到深地探测等涉及分层媒质中电磁波传播的领域。