基于不确定度理论改进的FKF 组合导航算法

魏德轩，曹 乐，韩学法

（上海工程技术大学 电子电气工程学院，上海 201620）

0 引言

随着无人机、无人车的发展，低成本组合导航系统的应用需求越来越多，对组合导航算法的精度、鲁棒性有了更高的要求。全球卫星导航系统（global navigation satellite system, GNSS）与捷联惯性导航系统（strapdown inertial navigation system,SINS）两种导航系统优势互补、成本低，在军用和民用领域有着广泛应用，是组合导航技术的热门研究方向。

目前针对GNSS/SINS 组合导航算法有基于人工智能领域的神经网络算法[1-2]和基于贝叶斯原理的传统信息融合算法。基于神经网络的组合导航算法，需要利用大量数据进行训练，效果受训练集数据影响较大。传统信息融合算法不需要大量数据进行训练，实时性好，其中卡尔曼滤波（Kalman filtering, KF）算法由于计算量小，对计算性能要求低，其应用更为广泛。在经典卡尔曼滤波组合导航算法中，综合利用了历史所有GNSS 的观测值，对SINS 进行校正，当滤波模型准确时，滤波的增益计算回路会逐渐收敛，新的观测值对状态估计的修正作用逐渐减小。因此，为了使状态估计能较好地适应观测值的变化，文献[3]开发了在线自适应遗忘因子滤波算法；文献[4]为了降低计算量，利用新息协方差计算渐消因子，提高了实时性；文献[5]为了提高滤波算法的精度和鲁棒性，设计了渐消记忆指数加权的新息协方差估计方法，并引入了多重渐消因子以实现对预测误差协方差阵的调节；渐消卡尔曼滤波（fading Kalman filter, FKF）效果较为依赖GNSS 观测值，然而GNSS 在城市高楼区、林荫道等场所易受干扰，噪声统计特性复杂[6]。为了降低GNSS 噪声的影响，文献[7]在低成本GNSS/INS 组合导航中，使用高精度实时动态差分（real-time kinematic, RTK）GNSS 定位，虽然有效提高了导航定位精度，但是RTK 定位需要基站，应用受到限制；为了能够实时获取GNSS 观测信息的噪声统计特性，文献[8]基于高斯白噪声假设，设计了基于χ2( )1 分布的滤波异常检测，对噪声的统计特性进行实时检测，实现了鲁棒渐消容积卡尔曼滤波算法；文献[9]利用最大相关熵的方法，对噪声进行预处理，得到了噪声的先验信息，在消除脉冲噪声的影响后，再进行鲁棒自适应滤波，提高了滤波精度；上述算法涉及大量矩阵运算，要求矩阵非奇异，计算复杂，对组合导航系统的运算性能要求较高。随着不确定度理论的发展，在导航定位领域也逐渐使用不确定度描述定位特性[10-11]，文献[12]结合测量不确定度理论，对GNSS模型进行了建模分析，利用3 个参数对7 个影响GNSS 信号质量的因素进行量化，得到相应的噪声统计特性，以此为基础改进了GNSS 观测噪声模型，提高了导航精度；但是这种方法需要事先采集大量GNSS 数据，对噪声统计特性进行建模分析，虽然实时应用受限，但是证明了GNSS 模型精度越高，导航定位精度越高。

基于上述分析，针对FKF 组合导航算法对于观测噪声突变而难以准确建模，从而导致定位精度较低、鲁棒性差的问题，本文以动态测量不确定度理论为基础，对GNSS 观测数据进行不确定度建模实时计算，定义了监测系数表示观测噪声先验信息，并据此对FKF 的组合导航算法进行改进，以提高滤波算法精度和鲁棒性。

1 基于FKF 的组合导航算法

1.1 组合导航系统方程

本文GNSS/SINS 导航系统采用松组合的结构方式，卡尔曼滤波器采用基于误差状态量的间接式结构，选用北东地坐标系为导航坐标系。低成本陀螺仪角度随机游走误差较大，使用互补滤波算法输出的姿态角进行导航信息融合，组合导航系统框图如图1 所示。

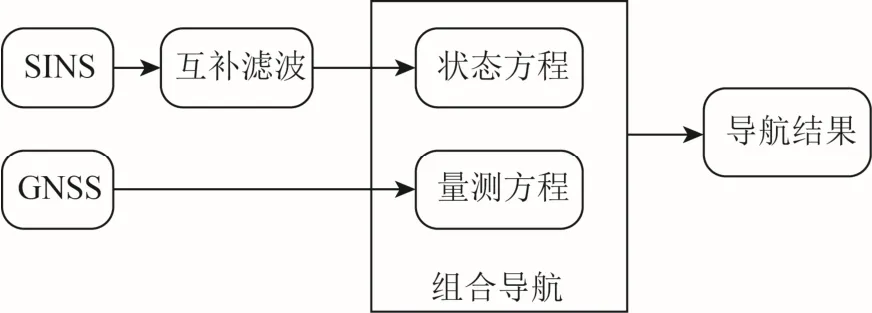
图1 组合导航框图

在k时刻，导航系统状态空间模型为

式中：Qk为非负的系统噪声序列方差阵；kR为正定的观测噪声序列方差阵；δkj为克罗内克（Kronecker）δ函数，当k=j时，δkj=1，当k≠j时，δkj=0。

误差状态卡尔曼滤波算法的预测和修正过程[13-14]为

1.2 渐消卡尔曼滤波算法

针对系统模型失准和噪声统计特性与实际环境不相符两种状况，FKF 的两种实现方式如图2 所示，分别是渐消因子法和膨胀系数法。

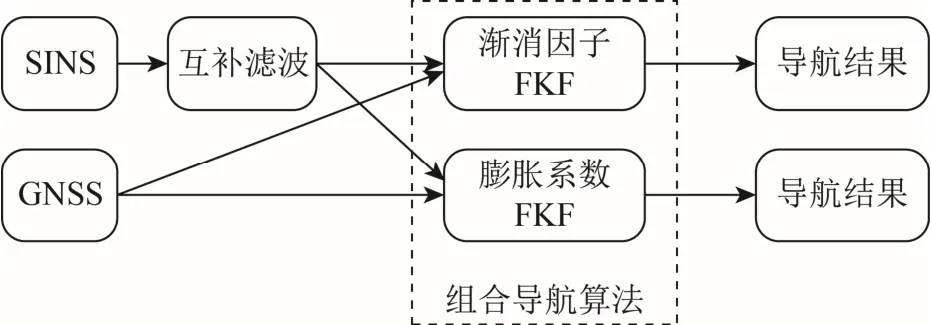
图2 FKF 实现方式

1.2.1 渐消因子法

通过增强k时刻GNSS 的量测值的权重，使得状态估计能更好地适应新的量测值的变化，此时渐消卡尔曼滤波算法的实现方式[3,5]为

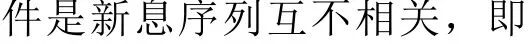
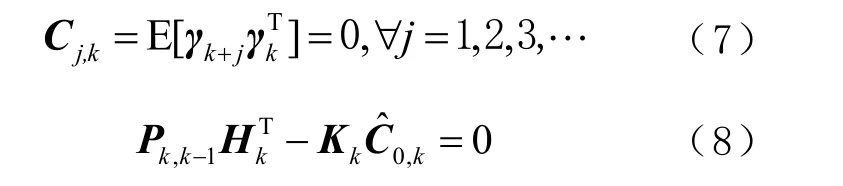
当系统模型失配时，实际的新息协方差矩阵与计算出的理论值不相等，致使式（8）不成立。此时通过式（5）计算得到kλ，实时调整Pk,k1-对Kk的影响，使式（8）保持成立，进而达到抑制滤波发散的目的。主要的思想是通过提高新观测量的权重抑制滤波发散，提高滤波精度。但是当观测噪声变大时，反而会导致导航误差增大，滤波精度降低甚至滤波发散。

1.2.2 膨胀系数法

针对噪声模型失配的问题，文献[15-16]提出了通过“膨胀”观测噪声矩阵来降低滤波增益的方案，当检测到量测噪声异常时，通过膨胀系数矩阵降低观测量的权重，调整公式为

式（13）意味着，当观测噪声的增大导致滤波精度下降时，新息矢量的协方差也会变大，对噪声矩阵进行“膨胀”，进而削弱观测量的修正作用，提高系统模型预测值的权重，避免因观测噪声的影响导致滤波发散，从而提高滤波器的鲁棒性。

2 基于不确定度理论改进的FKF 低成本组合导航算法

FKF 的两种实现方式原理不同：第一种算法是在系统模型失准、但噪声模型符合时，可以提高滤波精度；第二种算法是在系统模型较为准确、但观测值受到异常干扰时，可以在损失一定精度的条件下，保证滤波稳定，具有较强的鲁棒性。为了实现两种方式的有效结合，提高算法的自适应性、精度和鲁棒性，本文利用动态测量不确定度理论对GNSS 观测值建模分析。GNSS 定位信号的不确定度大小与接收机噪声、电离层效应、大气效应、星历误差、卫星时钟误差、多径效应和枝叶衰减等因素直接相关，直接测量这些误差因素的不确定度是不切实际的[12]，并且这些因素在车辆运动时，可能会发生较大的变化，无法将其作为静态常数。动态测量不确定度理论将GNSS 测量过程看做序列参数测量过程，可以按图3 所示分解为确定性成分与随机性成分[17]，分别利用多项式拟合和自回归模型（autoregressive model, AR）进行建模计算。

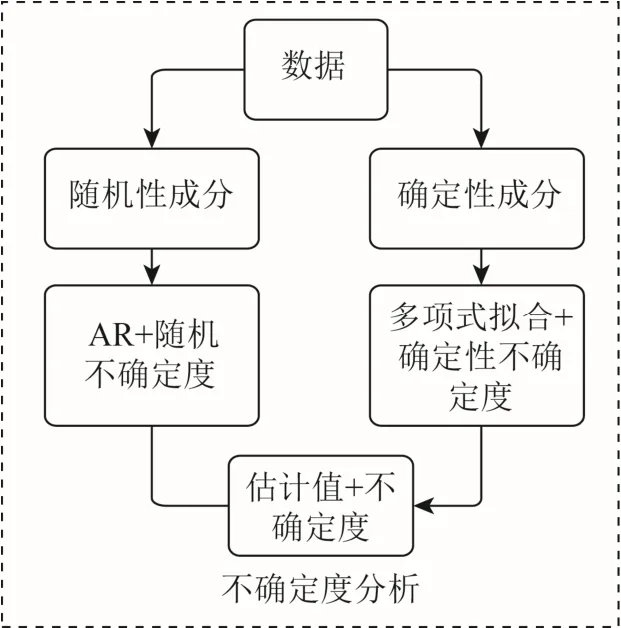
图3 不确定度分析框图

为了使算法既能在不确定度发生微弱扰动时保持稳定，又能同时敏感地检测到观测噪声的变化，本文定义了监测系数μ，结合变化量ΔS对不确定度进行分析后，选择FKF 的实现方式，改进后的组合导航算法实现过程如图4 所示。对GNSS 测量数据进行建模时，针对长为N的数据，观测数据X(i) 可表示为

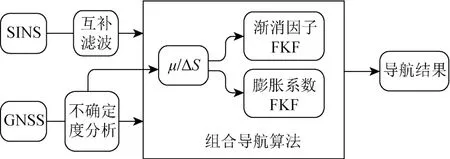
图4 改进后的组合导航算法系统框图

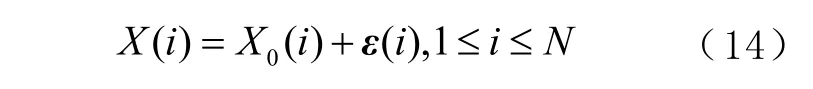
式中：X0(i)为真值；ε(i) 为测量误差。用不确定度的理论将X0(i) 和ε(i) 分别分解为确定性成分和随机性成分，即

式中：F0(i) 为确定性变化成分；Y0(i) 为随机性变化成分；εs(i)为系统误差；εr(i)为随机误差。各成分性质不同，根据图3 有

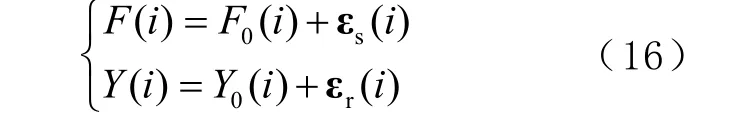
式中：F(i) 代表确定性成分；Y(i) 代表随机性成分。实际的测量数据通常由确定性成分和随机性成分组成，即

式中：0C、1C、2C为多项式拟合系数。确定性成分的A 类标准不确定度可根据式（19）计算。

计算随机性成分的不确定度时，将残差v(i) 记为新序列Y(i) ，由于残差v(i) 均值为零，可以看作是零均值的随机过程。序列Y(i) 长度固定且较短，本文选择AR 模型进行短期预测提取随机成分，其模型为

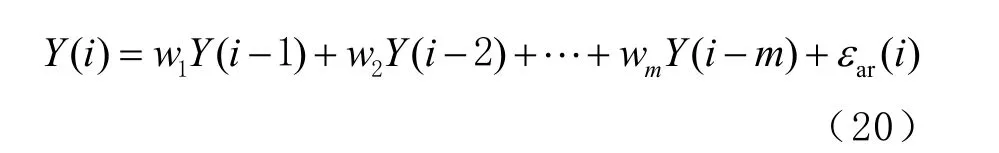
式中：m为模型的阶次；mw为待估计参数；εar(i)为估计的误差项，通常将其作为高斯白噪声，其均值、方差和相关性满足

式中：SN(i) 、SE(i) 、SD(i) 分别为北向、东向和地向测量值的不确定度；SGPS(i) 为GNSS 测量点的总不确定度；通过式（27）可得到GNSS 量测值的不确定度，为了降低观测数据中异方差的影响，对不确定度数据进行对数变换。相同噪声方差下的不确定度存在微弱扰动，仅通过不确定度的变化选择组合导航算法会降低算法鲁棒性。因此本文通过式（28）定义μ为相邻时刻不确定度的监测系数，ΔS为相邻时刻不确定度的变化量，即

3 实验与结果分析

3.1 数据集及数据处理

本文使用基蒂（Kitti）自动驾驶数据集中马拉加市区第二纪元的数据验证算法。路径轨迹如图5（a）所示，将RTK 校正修复后的全球定位系统（global positioning system,GPS）数据作为载体运动真值，输出频率1 Hz。惯性测量单元使用输出频率为100 Hz 的xSense MTi，3 轴加速度的静态误差偏差约为0.05 m/s2，3 轴瞬时角速度误差约为0.4 (°)/s[18]。载体坐标系为前左上，车载GPS 与惯性测量单元（inertial measurement unit, IMU）传感器在车体的安装位置如图5(b)所示，具体位置坐标如表1 所示。

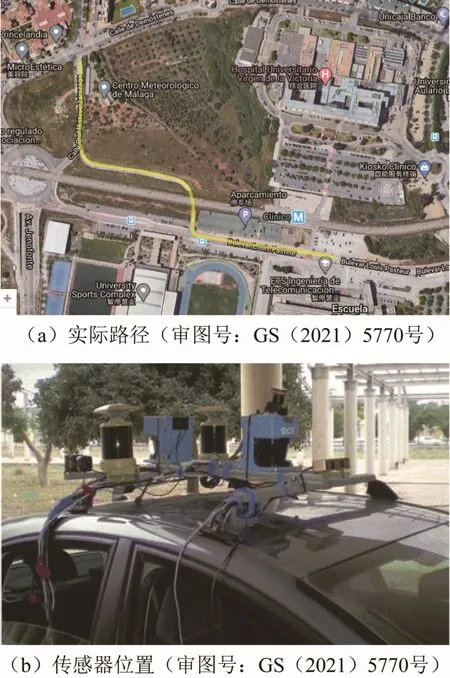
图5 数据集采集

为使GPS 数据与IMU 数据严格时间同步，对GPS 数据进行三次样条插值后按IMU 数据输出时刻抽取 GPS 数据，仿真时整体叠加方差为5 m 的高斯白噪声模拟GPS 信号精度，加入了两段方差为10 m 的高斯白噪声模拟突变噪声。图6为原始纬度、经度及海拔高度进行三次样条插值后，提取的频率为10 Hz 的数据。图7 为将GPS数据加噪声后转换为北向、东向、地向坐标系下的位置坐标。

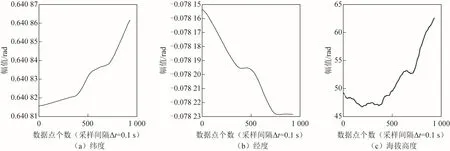
图6 原始数据

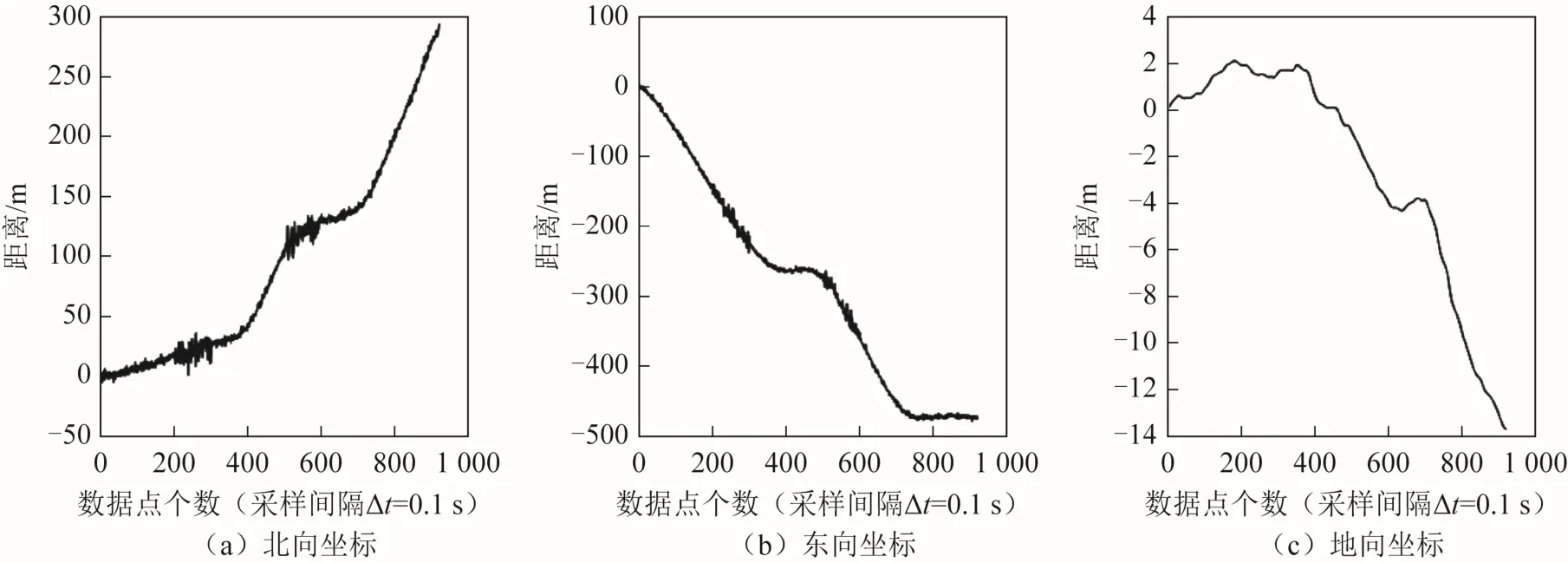
图7 噪声数据

3.2 结果分析

由式（27）可知，此时得到的不确定度为每个测量点的综合不确定度，数据中所加噪声及不确定度计算结果如图8（a）、图8（b）所示，进行对数变换后，计算得到的监测系数μ如图8（c）所示，能准确反映数据统计特性的突变。

图8 数据处理

由于低成本陀螺仪误差漂移较大，在组合导航系统中采用互补滤波进行姿态解算，此时姿态信息与比力、地磁关联较大，受GPS 量测噪声影响较小，无法体现本文中算法的效果。因此通过图9、图10 和表2、表3 列出各方向的位置误差和速度误差结果进行对比。

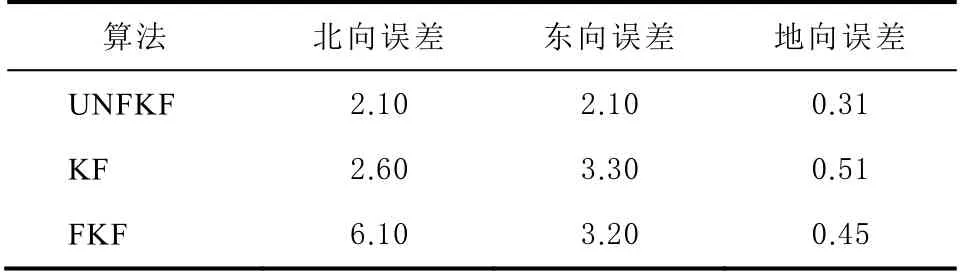
表2 三种算法位置最大误差单位：m

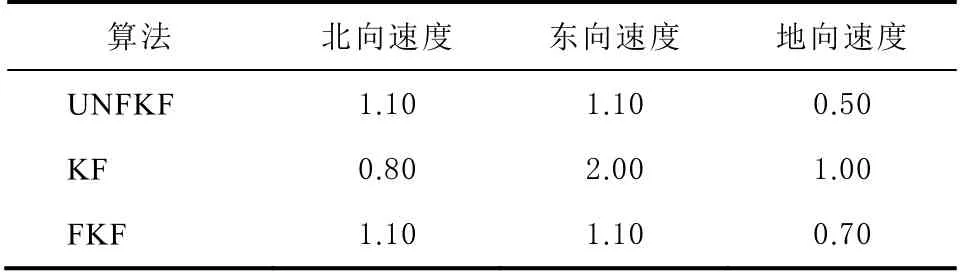
表3 三种算法速度最大误差单位：m/s

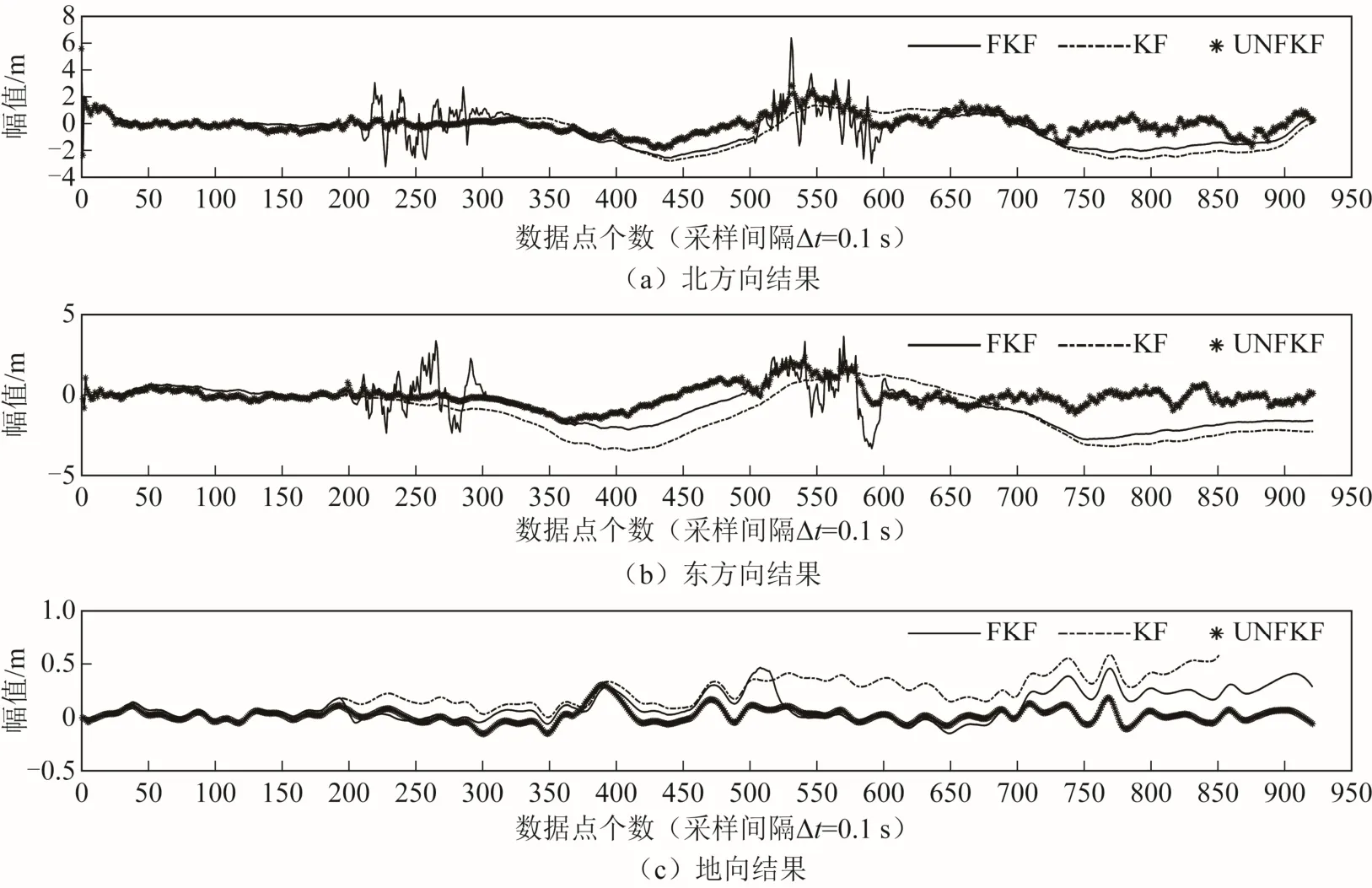
图9 位置误差

图10 速度误差

从图9 和图10 可以看出，误差状态KF 对噪声有一定的抑制作用，但是地向位置误差有发散的趋势，证明KF 算法鲁棒性不强且精度较低，最大误差约为3.30 m。当使用FKF 时，实际噪声与建模观测噪声匹配时精度有明显提高，但是当观测噪声增大时，反而更容易受到干扰，最大误差为3.20 m，鲁棒性较差。改进的UNFKF 在没有突变噪声干扰时，精度与FKF 相当。噪声突变时滤波精度降低，是因为噪声突变等价于观测信息的修正作用减小，IMU 的误差无法被校正，相比之下精度必然有所下降，最大误差为2.10 m，但滤波精度仍然比KF、FKF 高35%。当噪声稳定后，能继续保持滤波收敛，证明鲁棒性较高。在图10 速度误差图中，改进的算法在几种算法中北向、东向速度的最大误差没有明显降低，但是各向速度误差波动较小，并且载体总速度的最大误差相比KF降低了32%。

4 结束语

本文针对 FKF 算法在低成本组合导航应用中鲁棒性差、精度低的问题进行了研究，通过对FKF算法的实现方式进行分析，根据其原理的区别引入了动态测量不确定度建模的方法，对观测数据进行建模，实时计算不确定度，为了降低不确定度微小扰动的干扰，提高分析结果的准确度，定义了监测系数并结合不确定度变化量判断观测噪声统计特性的变化趋势，并根据观测噪声的变化选择FKF 的实现方式，最后使用Kitti 数据集进行仿真验证。结果表明：算法在异常量测噪声的干扰下能够保持较强的鲁棒性和自适应性，且收敛速度快，位置误差精度提高35%，总体速度误差降低32%。下一步将研究针对各个维度不同噪声统计特性下的不确定度的多渐消因子的自适应改进算法。