基于LSTM-GA的股票价格涨跌预测模型

刘瑜儒 周龙武 庞利

摘要：在量化金融领域中，如何对股票价格进行准确的预测，成为当前研究的重要问题。LSTM网络算法的出现，较好地解决了股票价格预测的复杂序列化数据学习问题。但是，当前研究结果表明，若是单一采用LSTM算法仍然存在预测不平衡、局部极值不准确等问题。GA（遗传算法）的解释在当前金融界中尚没有一定准确定论，但是其在解决调参问题上有着突出效用。在构建新型股票价格预测模型时，首先可以采用LST神经网络算法对收盘价进行预测，然后采用GA遺传算法保证模型预测的准确性，通过辨别机制，最终获取股票价格涨跌信号。基于此，文章针对现有LSTM模型的原理及应用进行了综合分析，并突出说明了LSTM-GA在股票价格预测领域中的应用。

关键词：LSTM记忆神经网络;GA遗传算法;股票;价格涨跌预测模型

随着金融市场的发展，股票价格的预测一直以来都受到人们的关注。然后，股票市场受到的因素较多，对其趋势预测的波动性较大，不仅预测算法较为复杂，还会受到现实情况的掣肘，从而导致预测结果不准确。传统股票价格预测技术大致可以分为技术预测和聚类预测两种类型。本文主要是基于技术预测的基础之上，探究当前LSTM长短期记忆神经网络在股票价格预测中的突出效用，然后充分采用ANN（人工神经网络）、时间序列模型、SVM向量机以及技术预测中的随机性算法来优化股票价格涨跌预测模型。

随着当前智能化技术的深入，ANN（人工神经网络）在处理复杂关系问题上面，被证实了有着突出的作用，但是，由于受到网络测试和人工速度的影响，计算效率较为缓慢。此外，由于ANN还存在陷入局部极小值、过渡拟合以及黑盒技术的缺点，并不能直接被用于股票价格涨跌预测之中;SVM支持向量机的特征是在选择过程中不能有效表现出最优的个数特征，这将严重影响到股票价格涨跌模型系统的精准度。当德国Krauss教授将随机森林算法融入到股票预测之中时，股票价格涨跌模型取得了良好的效果。在Fischer等人的研究中，是将任何一种机器学习模型作为随机算法的有力基准，充分采用了GARCH时间序列模型，并将之充分运用到股票价格涨跌算法之中。其主要是假设时间序列值是呈现线性的生成过程，因此，具有一定的局限性。毕竟在股票市场之中，其涨跌特点不可能呈现线性增长，其价格的涨跌是与运营商的政治经济条件和战略主张息息相关。因此，其中GARCH方法中假设金融时间序列将不能使用到LSTM长期记忆神经网络之中，这也让其时间序列算法更加复杂。Fischer等人再次通过LSTM 模型来针对每日股票数据集进行预测，并针对其收盘价格与开盘价格的分析，来预测其价格涨幅的规律。实验结果表明，采用LSTM结合SVM算法对股票价格涨跌得到预测准确率一般处于51%～54%之间，这样的算法虽然比随机算法更加优秀，但是，却无法准确地精算，依然受到局部极值的影响，计算出来的数值也存在精准度不高的情况。而在后来研究者中，有部分研究者对整体模型参数进行了调整，充分结合了多维度数据处理特征样本。本文就是基于这样的情况下，提出基于LSTM长短期记忆神经网络的机器随机算法来预测股票价格涨跌，并在此基础上加入GA基因算法来加以改进，从而提升预测准确性，充分弥补了采用LSTM网络技术的不足。

一、LSTM长短期神经网络技术的原理及应用

LSTM网络技术最早是由Hocketer等人提出来的，2000年，schmiduber等人对其技术进行了改进与提升，并提出了一种适用于连续性预测的遗忘门方法。Grave在之后的树种也提出了对LSTM 的改进方法，并解释了相关的许多问题，进一步推动了LSTM网络在量化金融领域中的应用。

神经LSTM网络的前身是循环神经网络。RNN（循环神经网络）主要是通过内部循环学习序列模式，在其中形成了多个网络回路，能对其参数进行自主学习和对权值进行调整，从而能不断传递相关信息，并通过反向传播来增加链式规则和数据分布。在反向传播过程中，返回的数值将激活sigmoid和tanh函数，当其火花函数呈现最小值或者是梯度消失梯度爆炸等问题的时候，将出现无法避免的数值丢失与预测问。而LSTM网络技术模型的应用，就是为了有效避免这些问题的发生。Hocker等人在充分研究之后，提出了储存单元和数据库的理念，从而让返回的数值能进行长时间储存，并对其信息进行分析，剔除一些不必要的信息。

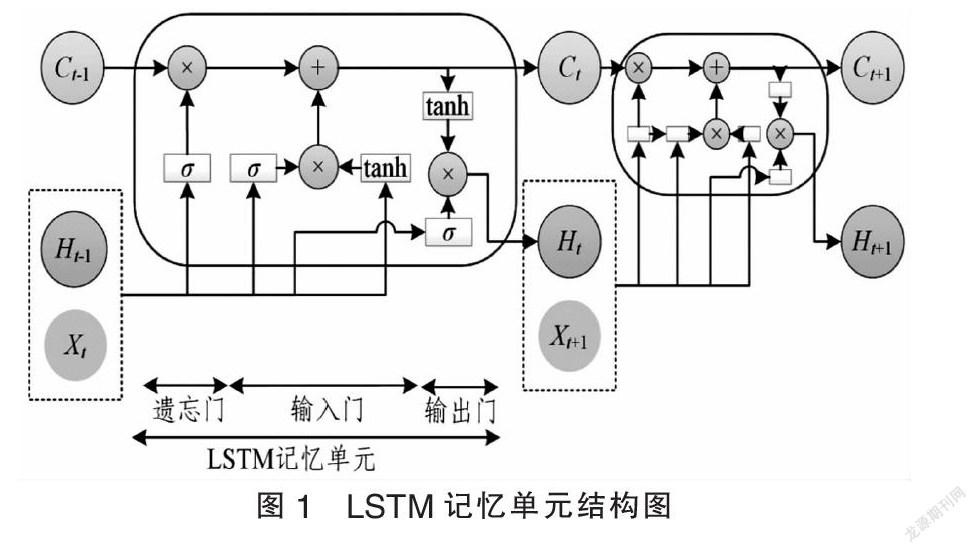
LSTM网络技术是一种允许神经元替换的方法。LSTM存储单元的具体结构如图1所示。LSTM单元由一个存储单元（Ct）和三个门组成，包括输入门（it）、遗忘门（ft）和输出门（ot）。这样的数据表明，在时间t，χt表示输出数据和ht隐藏位置时，符号“×”表示向量的外积，而“+”符号表示叠加操作。

具体运算公式如下：

ft=σ（Ufχt+Wfht-1+bf）

it=σ（Uiχt+Wiht-1+bi）

ut=tanh（Uuχt+Wuht-1+bu）

Ct=ft*ct-1+it*ut

Ot=σ（UOχt+Woht-1+bo）

ht=ot*tanh（ct）

在此公式中，W、U代表的是矩阵权重，而b代表的是偏移量，σ代表的sigmoid函数，符号*代表的是向量外积。

遗忘门的计算就是将χt，ht-1，bf进行权加和，然后再通过sigmoid函数得到ft（ft∈（0，1）），如式列ft=σ（Ufχt+Wfht-1+bf）。而其中ft表示的是上一个记忆细胞在（Ct-1）中需要被遗忘的信息权重。换句话说，就是通过遗忘门来对上一个记忆细胞中保留的信息量加以控制，同时运用Ct=ft*ct-1+it*ut式子来计算。而其中输出门中的（Ct）则决定了其可以接受到多少量级的记忆细胞信息，用it=σ（Uiχt+Wiht-1+bi）来进行计算。最后将采用Ot=σ（UOχt+Woht-1+bo）输出门来过滤（Ct）。待原来记忆细胞过滤完全之后，将通过ht=ot*tanh（ct）来获得当前ht的状态，最后进行反向传播，而LSTM模型就是由这些储存块相互计算而得出来的。