激光冲击下CoCrFeMnNi 高熵合金微观塑性变形的分子动力学模拟1)

杜 欣 熊启林 周留成 阚前华 蒋虽合 张 旭 ,2)

* (西南交通大学力学与工程学院,成都 610031)† (华中科技大学航空航天学院,武汉 430074)

** (空军工程大学等离子体动力学重点实验室,西安 710038)

†† (北京科技大学新金属材料国家重点实验室,北京 100083)

引言

激光冲击强化技术利用激光穿过约束层,作用于烧蚀层产生大量等离子体,等离子体继续吸收激光能量发生爆炸从而产生冲击波作用于金属表面.当冲击波峰值压力大于材料的屈服强度时,激光冲击使材料发生超高应变率(＞106s-1)的塑性变形,造成材料表面出现残余压应力分布并且发生表面晶粒细化[1-3].与传统的机械处理技术相比,激光冲击强化后材料的粗糙度得到很好的改善,并且磨损寿命和疲劳强度得到了提高[4-5].因此,目前激光冲击强化技术已经在航空工业中得到广泛应用[3].

高熵合金是具有多个化学主元(通常大于4 种)的新型结构材料[6],多主元并未使高熵合金变脆,反而表现出更好的性能,例如高硬度、高强度、良好的塑性、出色的热稳定性和耐腐蚀性[7-11].这些优异的性能使得高熵合金在工程中的潜在适用性受到了广泛关注.CoCrFeMnNi 作为一种典型的高熵合金,最早由Cantor 等[12]在2004 年提出,所以也称为“Cantor 合金”,其晶体结构为面心立方,在室温(300 K),低温(77 K)和超低温(15 K)下具有出色的强度和塑性变形能力[13-15].这些优异的性能使得CoCrFeMnNi 高熵合金未来有望在天然气输运、航空航天等领域运用.由于激光冲击强化技术已广泛应用于航空航天等领域,所以研究CoCrFeMnNi 高熵合金的激光冲击强化有重要的意义[16].

分子动力学模拟是基于经典牛顿力学对原子或者分子的运动进行模拟的方法,有助于揭示材料在原子尺度上的力学行为和变形机理[17].利用分子动力学来模拟激光冲击,可以直观观察到冲击过程中以及冲击之后材料微观组织的演化过程.许多学者针对激光冲击强化问题,开展了分子动力学相关研究.例如,Meng 等[18]研究了激光冲击波在Al-Cu 合金中的传播过程,发现温度会影响扩展位错的形成和演化,并且弹、塑性波速度随温度的升高而减小.Xiong 等[19]研究了铜单晶受冲击压缩的弹塑性双波结构,指出由冲击波引起的缺陷形态表现出明显的晶体取向依赖性.陈亚洲等[20]发现在激光冲击下纯钛内部产生了孪生变形,变形孪晶生长经历了沿垂直加载方向生长、无序生长、形成孪晶栅3 个过程,得到了弹塑性波分离的双波结构.徐高峰等[21]研究了激光冲击纯钛的温度效应,指出在深冷条件下(77 K),冲击波的速度高于常温条件,能够产生稳定的弹、塑性双波结构,产生的高密度堆垛层错钉扎了位错,从而实现材料强化.Germann 等[22]发现在某些冲击方向下,在波阵面附近由于原子面间的弹性振动产生了独立的波列.Bringa 等[23]发现激光冲击产生的高应力会阻碍晶界运动,限制了材料的软化.上述研究都采用分子动力学模拟方法,分析了冲击波传播过程以及冲击波作用于材料的微观机理.然而,目前针对CoCrFeMnNi 高熵合金激光冲击强化的分子动力学模拟鲜见报道,这限制了从原子尺度上理解CoCrFeMnNi 高熵合金激光冲击过程中的微观结构演化、冲击波响应.

针对以上问题,利用分子动力学模拟软件Lammps[24],对单晶CoCrFeMnNi 高熵合金进行了激光冲击的分子动力学模拟.通过位错提取算法(dislocation analysis,DXA) 以及共邻分析方法(common neighbor analysis,CNA)来分析不同冲击方向下微结构演变过程[25-27],并且通过粒子速度以及冲击波波速来分析不同冲击方向下的冲击波特性,此外分析了冲击后残余应力与位错密度沿冲击深度的分布.

1 原子模型与加载方式

为研究冲击时双波结构以及微结构演化的取向相关性,利用Atomsk 软件[28]分别建立尺寸为74.7 nm × 13.3 nm × 7.5 nm,取向为x=[100],y=[010],z=[001],x=[110],y=,z=[001]和x=[111],的3 个单晶CoCrFeMnNi 高熵合金模型(晶格常数a=3.595 Å),其中x方向为[100]取向的单晶模型如图1 所示.此外,作为对比分析,建立了与CoCrFeMnNi 高熵合金具有相同尺寸及取向的纯Ni 模型.在冲击之前,采用NPT 系综使体系在300 K 下弛豫50 ps 来达到热力学平衡,弛豫时,x,y和z方向采用周期性边界条件,时间步长为1 fs.冲击加载时,冲击方向(x方向)为自由边界条件并采用NVE 系综.

图1 x 方向为[100]取向的单晶CoCrFeMnNi 高熵合金原子模型Fig.1 Atomistic model of single crystal CoCrFeMnNi high-entropy alloy with [100] orientation in x direction

CoCrFeMnNi 高熵合金的分子动力学模拟采用Choi 等[29]提出的第二近邻修正嵌入原子(2 NN MEAM)势函数,该势函数已被用于模拟CoCrFeMnNi高熵合金的循环变形、压痕、温度以及应变率效应[30-33].基于该势函数构建的高熵合金模型径向分布函数如图2(a)所示,可以看出其径向分布呈现平滑分布的特征,这与传统的面心立方结构(facecentered cubic,FCC)合金径向分布函数中表现出的单峰特征有所不同,体现了高熵合金的的晶格畸变效应[34-35].此外,在该势函数下构建的CoCrFeMnNi高熵合金原子模型的所有第一近邻键对的键长满足高斯分布,如图2(b)所示.

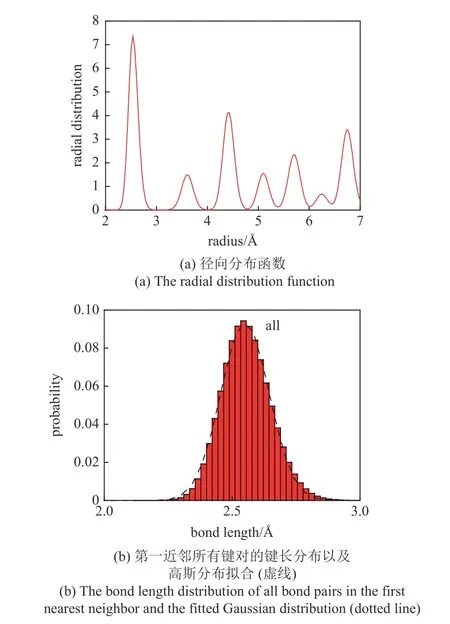
图2 径向分布函数与第一近邻所有键对的键长分布Fig.2 The radial distribution function and the bond length distribution of all bond pairs in the first nearest neighbor

在分子动力学模拟中,有3 种方法产生冲击波:(1)收缩性边界条件法,通过收缩边界产生由两侧向内部传播的冲击波,常用在流体冲击波的模拟;(2)对称碰撞法,通过将材料与飞片发生碰撞来产生冲击波;(3)活塞法,通过将边界处一定层数的原子作为活塞来诱导冲击波的产生[1].在本文中采用活塞法来进行激光冲击的分子动力学模拟,取x方向边界处三层原子作为活塞,其中活塞原子速度为Up,产生的冲击波速度为Us.只有冲击波引起的应力大于其Hugoniot 弹性极限,才会使材料产生动态塑性变形,从而有可能产生弹性波和塑性波分离的双波结构.材料的Hugoniot 弹性极限 σHEL可表示为[19]

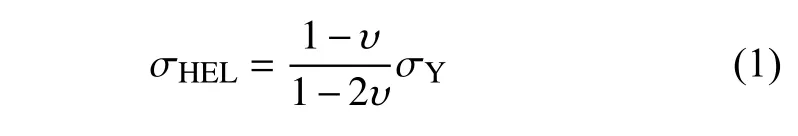
式中,υ 为泊松比,σY为屈服应力.由于弹、塑性双波结构的产生,冲击强化材料分为5 个区域,即活塞区、塑性区、弹塑性区、弹性区和未受冲击区[19],如图3 所示.

图3 活塞法冲击强化材料的结构分区示意图Fig.3 Schematic diagram of the piston method

2 结果与分析

2.1 粒子速度

以1.2 km/s(高于Hugoniot 弹性极限)对单晶沿3 个方向进行冲击加载,冲击总时间为5 ps,并沿冲击方向进行分层处理,取每层质心位置作为冲击距离[36].在高应变率下,局部区域的粒子速度由原子的平移和热运动这两部分构成,而大多情况下,原子的热运动速度是其运动速度[37].所以,将除去质心速度后的平均粒子速度作为局部区域内的粒子速度,得到1 ps 和5 ps 时的粒子速度剖面图,如图4 所示.在冲击时间为1 ps 的冲击初期,由于受冲击区域较浅,导致沿各冲击方向冲击都未有明显的弹、塑性双波分离现象.在冲击时间为5 ps 时,沿[100]方向冲击时曲线并未出现台阶段,即并未出现弹塑性双波分离现象,而沿[110]和[111]方向冲击时产生了弹性波与塑性波分离的双波结构.这是由于[100]方向有更多的滑移系(8 个滑移系)激活,导致滑移更容易发生,以至于有更显著的塑性变形,造成塑性波的传播加快,从而引起弹、塑性波的分离不明显.而在[110]密排方向(4 个滑移系激活)和[111](6 个滑移系激活)冲击时塑性波较当前冲击方向下的弹性波波速慢,表现出了明显的弹、塑性双波分离现象.但是,当冲击速度提升到一定程度之后,沿[110]以及[111]冲击时的塑性波将追赶上弹性波,从而也不再表现出弹、塑性波分离的双波结构[38].

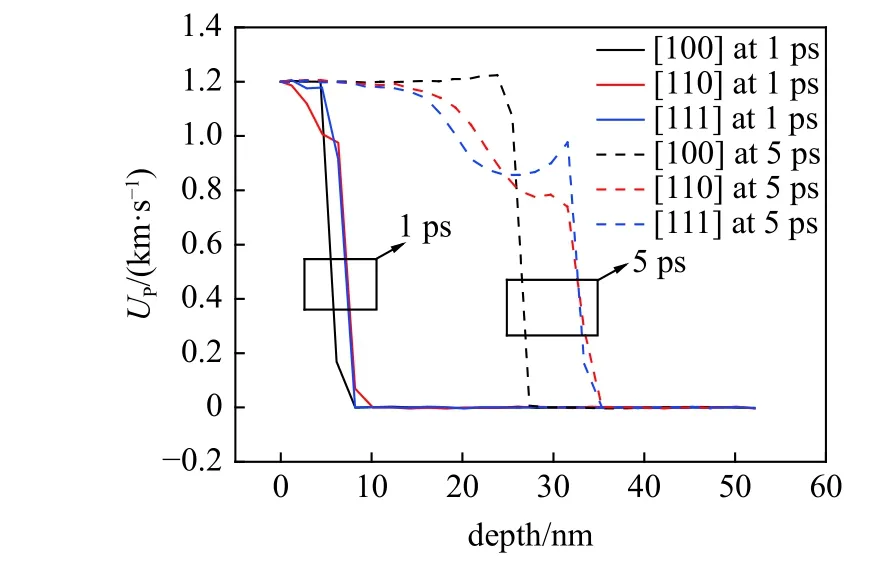
图4 粒子速度剖面图Fig.4 Particle velocity profile

由图4 可以明显观察到沿不同方向进行冲击时的冲击波波速的差异.在沿[100]方向进行冲击时其塑性波波速明显快于其余方向.沿[110]方向进行冲击时其塑性波波速略快于沿[111] 方向进行冲击时的塑性波波速,这与[110]方向为其密排方向有关.但是,沿[111]方向进行冲击时,由于弹性波的单独扰动,使得原子面在波前附近处弹性振动,导致附近粒子速度上升,从而产生了独立的波列[23].CoCrFeMnNi 高熵合金表现出的弹塑性双波分离现象和原子面弹性振动的取向效应与目前所研究的Cu 和Al 等面心立方结构金属结果一致[2,39].此外,可以看出沿[111]方向进行冲击时产生塑性波的临界冲击速度(约0.9 km/s) 大于[110] 方向(约0.8 km/s).临界冲击速度的差异与可开动滑移系的Schmid 因子大小有关.沿[111]方向加载时Schmid因子为0.272,而[110]方向的可开动滑移系Schmid因子为0.408,所以沿[111]方向进行冲击时所需要的外加应力更大,导致了其临界冲击速度大于[110]方向.但是,由于沿[100]方向冲击时的粒子速度剖面图未表现出弹、塑性双波分离现象,所以不能从中判断出[100]冲击方向下塑性变形发生的临界冲击速度.

2.2 局部应力

冲击加载时的应力状态可以反映冲击波特性以及微观组织变化,在这里计算了冲击1 ps,5 ps 时各区域的正应力 σxx、最大分切应力 σshear、等效应力σvm,如图5 所示.其中,最大分切应力 σshear和冯·米塞斯等效应力 σvm可表示为[1]

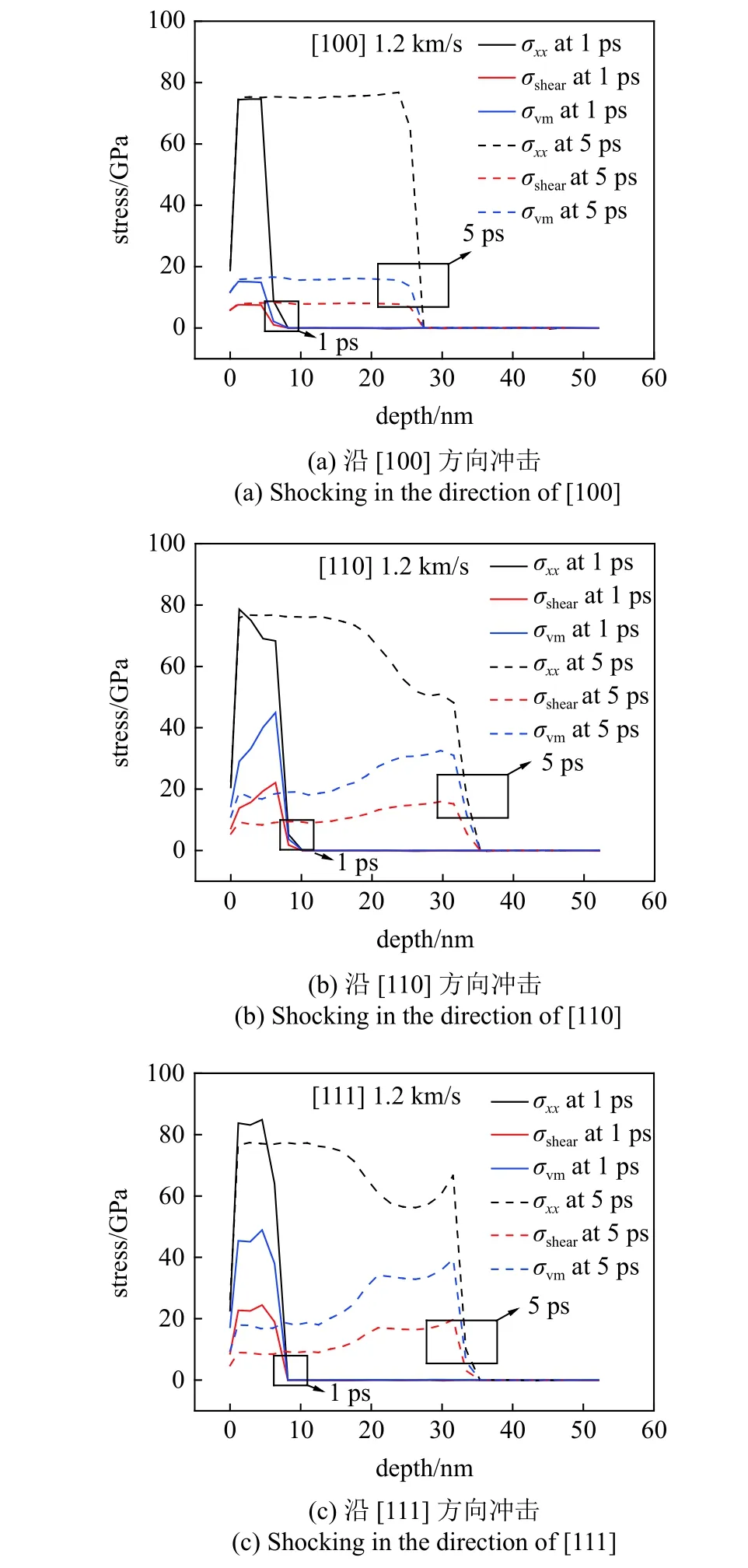
图5 局部应力Fig.5 Local stress

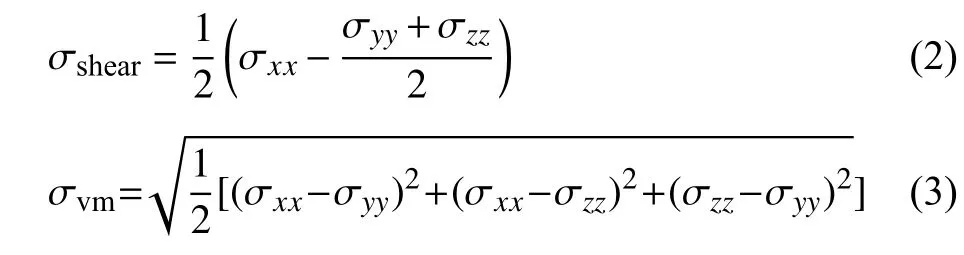
从图5 可以看出,沿[100]方向进行冲击时,首先出现弹性先驱波,正应力、最大分切应力、冯·米塞斯等效应力在波前附近急剧下降,未表现出弹、塑性双波分离现象.其余方向下正应力随着深度的增加有明显的台阶段出现,表明弹塑性双波已分离,此时台阶段只存在弹性波的扰动.而最大分切应力和冯·米塞斯等效应力在靠近冲击表面处较小,这是由于受到冲击载荷的作用,材料未表现出明显的泊松效应,导致材料处于静水应力状态[19].正应力、最大分切应力和冯·米塞斯等效应力在波前的急剧下降表明了模型中受冲击区域向未受冲击区域的转变.沿[111]方向进行冲击时,波前附近的局部应力增加同样表示着由于原子面之间的弹性振动导致出现的独立的波列.

沿[100],[110],[111] 3 个方向进行冲击时压力分布情况如图6 所示.可以看出,在沿[111]方向进行冲击时其Hugoniot 弹性极限(Hugoniot elastic limit,HEL)大于[110]方向,这同样与[111]方向可开动滑移系的Schmid 因子大小有关.但是,由于沿[100]方向进行冲击时的压力分布同样未表现出弹、塑性双波分离现象,所以不能直观获得其Hugoniot弹性极限[19].

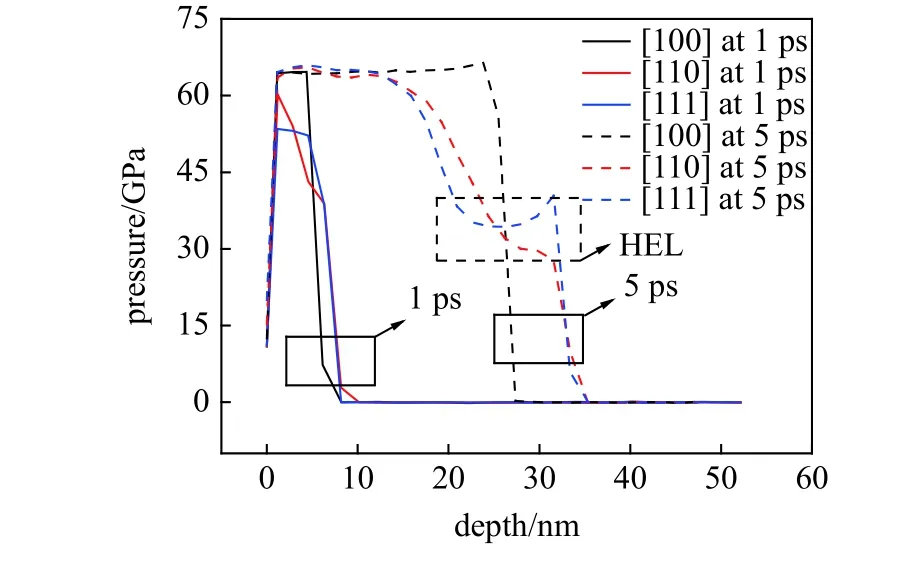
图6 压力分布Fig.6 Pressure distribution

2.3 微观结构演变

采用位错提取算法(DXA)分析位错密度沿深度方向的分布,如图7 所示.CoCrFeMnNi 高熵合金冲击过程中沿深度方向位错密度先增后减,表现出明显的位错密度梯度分布.在冲击表面附近处位错密度先增加,是由于在在冲击表面附近处最大分切应力较小.较小的最大分切应力造成位错诱导的塑性变形受限,从而影响冲击表面附近的位错成核以及增殖,使得位错密度呈现沿深度方向先增加后减小的梯度分布.分析位错密度的大小以及峰值出现的位置可以看出,在[110]冲击方向下位错密度峰值所对应的深度最深,沿[100]方向进行冲击会有更多的滑移系开动,但是其位错密度最小.其中,由于[110]冲击方向为密排方向,所以其塑性波传播速度略快于[111]冲击方向,导致其位错密度峰值所对应的深度最深.而[111]冲击方向较[110]冲击方向拥有更多的可开动滑移系,所以其塑性区域的位错密度大于[110]冲击方向的位错密度.此外,CoCrFeMnNi高熵合金由于晶格畸变降低了位错成核的能垒[40],导致了高熵合金冲击过程中的位错密度大于纯Ni.但是,在纯Ni 中以1.2 km/s 沿[111]方向进行冲击时只出现了弹性波,未发生塑性变形.在纯Ni 中沿[111]方向以1.2 km/s 进行冲击未产生塑性变形反映出了在此冲击方向下的临界冲击速度大于[100]和[110] 方向,这与在CoCrFeMnNi 高熵合金在[111]方向下拥有更高的临界冲击速度相同.同样,在纯Ni 的冲击加载过程中也产生了沿冲击深度方向先增后减的梯度位错密度.

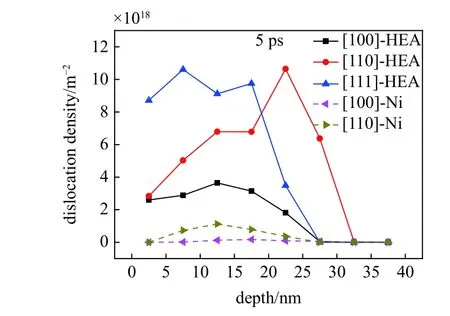
图7 位错密度分布Fig.7 Dislocation density distribution

沿[100]方向进行冲击时拥有最小的位错密度是由于其产生了体心立方(body-centered cubic,BCC)中间相,导致了更少的不全位错形核,如图8所示.图中3 个及以上蓝色原子层表示为BCC 中间相,绿色原子为FCC 结构,红色原子为密排六方(hexagonal close-packed,HCP)结构.围绕两个或多个FCC 原子层的一层HCP 原子层是一个孪晶界,两个相邻的HCP 原子层构成内层错,两个HCP 原子层夹一层FCC 原子层构成外层错,白色原子部分表示无序结构[28].在冲击过程中材料内塑性波传播的区域产生了大量的层错以及无序结构[27].此外,在冲击过程中产生了大量的扩展位错,进一步提高位错滑移的阻力,从而促进位错的进一步增殖.高密度位错使周边晶格发生畸变,导致原子排列呈无序化,产生了无序结构.从缺陷在材料内的分布深度可以看出在沿[110]方向冲击时塑性波传播快于[111]方向.

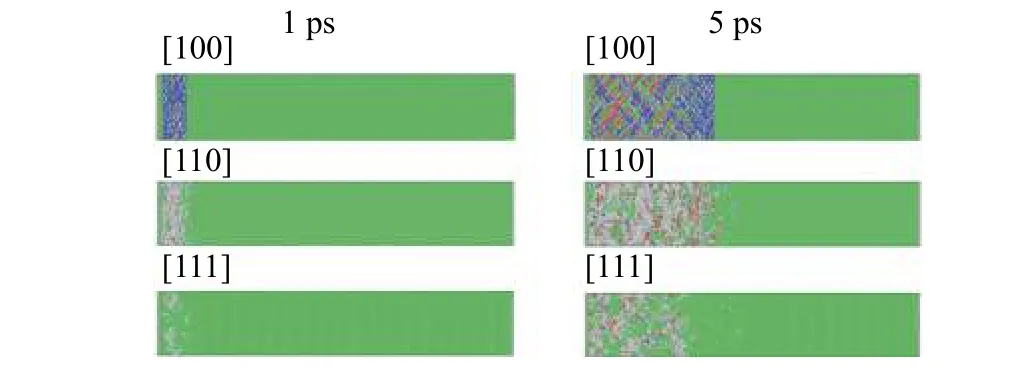
图8 采用共邻分析方法分析微观组织变化Fig.8 Microstructure evolutions by CNA

将CoCrFeMnNi 高熵合金与纯Ni 在冲击时间为5 ps 时受冲击区域内的微结构进行对比,如图9所示.可以看出,由于高熵合金中存在的晶格畸变效应,使得其在冲击过程中更容易发生晶格失配[40].导致了在高熵合金中产生的无序结构含量高于纯Ni,但在[100]冲击方向下高熵合金产生的BCC 中间相含量低于纯Ni.

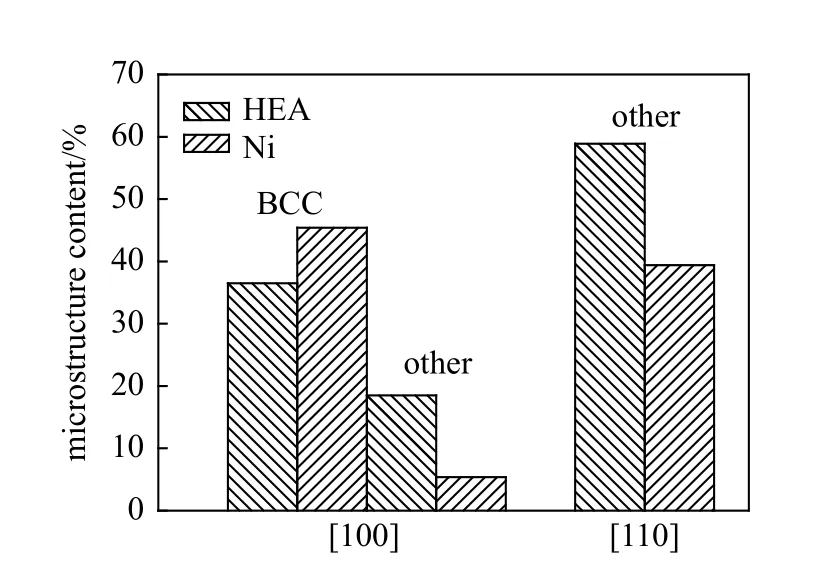
图9 冲击时间为5 ps 时CoCrFeMnNi 高熵合金与纯Ni 受冲击区域内微结构含量Fig.9 The microstructure content in the impact area of CoCrFeMnNi HEA and pure Ni at 5 ps

FCC 晶胞中的面心原子和与之相邻的FCC 晶胞中的面心原子以及共边顶角原子和共面的面心原子可以构成一个体心四方 (body-centered tetragon,BCT)结构,如图10 所示.图中绿色直线构成了两个相邻的FCC 晶胞,蓝色直线构成了一个BCT 晶胞.

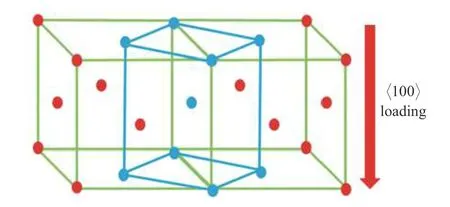
图10 FCC 结构中的BCT 结构示意图Fig.10 Schematic diagram of BCT structure in FCC structure

在沿[100]方向进行冲击时,由于冲击波高压作用导致FCC结构中BCT晶胞的高度从a压缩至与其横向长度相同的高熵合金的晶格常数),使得BCT 结构转变为BCC结构,进而表现出FCC 结构向BCC 中间相转变的现象[39].在沿FCC 结构的〈100〉晶向方向进行加载时,FCC 结构在冲击波作用下是否稳定可通过修正的Born 稳定性准则来判断,即[41]

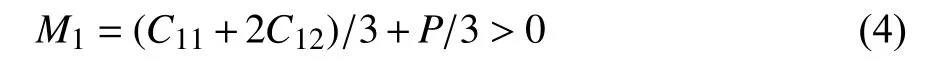
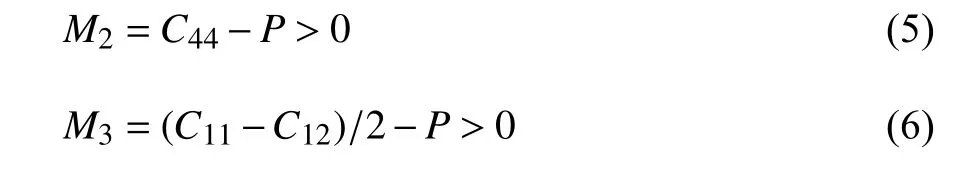
式中,M1为自旋稳定准则,M2为剪切稳定准则,M3为Born 稳定准则,P为压力,Cij为完美晶体的弹性常数.局部压力沿冲击深度方向分布如图11 所示,可以看出,在受冲击区域的压力超过了Born 稳定准则的临界压力,但是未达到剪切稳定准则的临界压力.因此,在沿[100]方向进行冲击加载时FCC 结构中的BCT 结构不稳定并转变为BCC 中间相.由于裂纹尖端的应力集中,使得这种压力相关的相转变机制也出现在裂纹扩展的分子动力学模拟中[42-43].

图11 沿[100]方向冲击时压力分布Fig.11 Pressure distribution at [100] shocking direction

为了探究高熵合金沿[100]方向冲击时BCC 中间相的演化情况,提取冲击为1 ps 时受冲击区域的微结构在随后冲击过程中的演化情况,如图12 所示.可以看出,BCC 中间相在随后的冲击加载过程中会逐渐转变为FCC 结构,并且有部分FCC 结构会转变为HCP 结构(层错).BCC 相在结构上不稳定并且两相间能垒随着压缩应力的减小而减小,导致了在随后的冲击加载过程中部分BCC 相转变回FCC 结构[41].高位错密度以及位错芯区域原子严重错排,导致了在冲击过程中产生了大量无序原子.

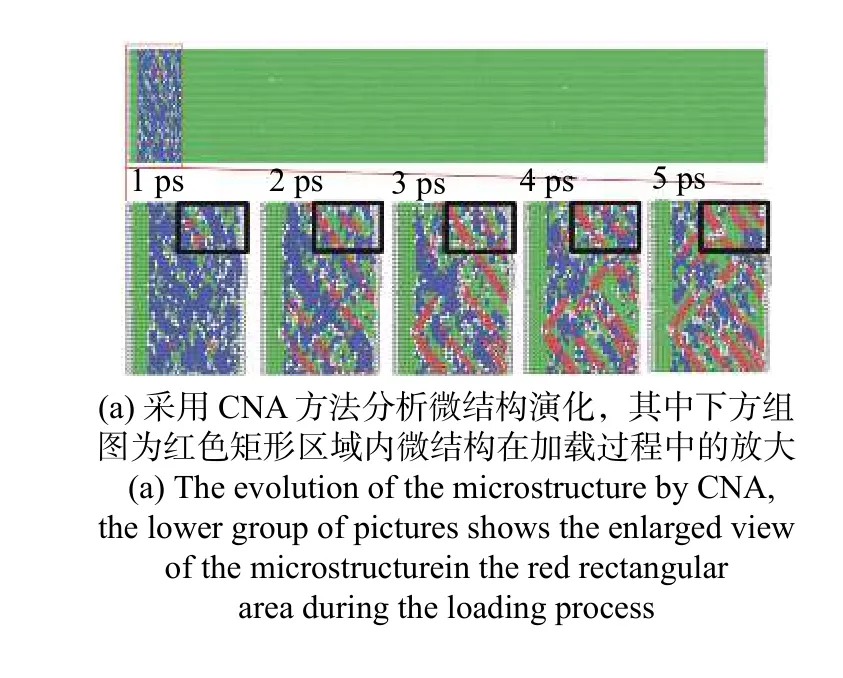
图12 高熵合金中沿[100]冲击方向下微结构演化Fig.12 Microstructure evolution at [100] direction in HEA

2.4 冲击后残余应力与位错密度

将模型两端固定,中心区域采用NVE 系综使冲击波在模型内充分传播,以达到保载的目的,保载过程中冲击波经历了多次反射的过程.沿[100]方向冲击后保载过程中冲击波的传播造成微结构变化的情况如图13 所示.BCC 中间相的产生与冲击波的继续传播以及反射密切相关,在塑性波进一步传播时的波前附近会产生BCC 中间相,而在冲击波已传播过的区域中,BCC 中间相会转变为FCC 结构以及层错.并且,在冲击波到达模型另一端的固定端时会发生反射,造成该区域内的压力增加,从而产生大量的BCC 中间相.但是,随着冲击波的衰减,后续产生的BCC 中间相含量减少,甚至在保载完成后不存在BCC 中间相,只存在层错以及无序结构.

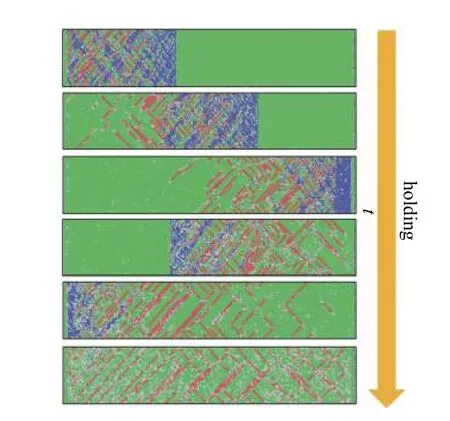
图13 沿[100]方向冲击后保载过程的微结构演化Fig.13 The microstructure evolution of the holding process after shocking in the direction of [100]

当全局应力达到平稳水平时认为保载完成,随后取消模型两端约束,在NVE 系综下弛豫以达到卸载的目的,当全局应力为零时认为卸载完成[44].卸载后获得冲击方向残余应力分量 σxx随冲击深度的变化情况如图14 所示.可以看出,在冲击表面为残余压应力,芯部为拉应力.由于冲击波的反射,造成了残余应力表现出了双向冲击的分布情况[45].沿单晶[100]方向冲击时芯部的残余拉应力最大.沿[111]方向冲击时较[110]方向拥有更多的可开动滑移系,导致[111]方向受冲击区域的塑性变形更加剧烈,造成在[111]方向冲击表面的残余压应力大于[110]方向.虽然沿[100]方向进行冲击时可开动滑移系最多,但中间相的产生导致了冲击后冲击表面附近的残余压应力小于沿[111]方向冲击后的残余压应力.值得注意的是,冲击以及保载过程中的约束层原子对残余应力的大小产生了一定的影响[46].

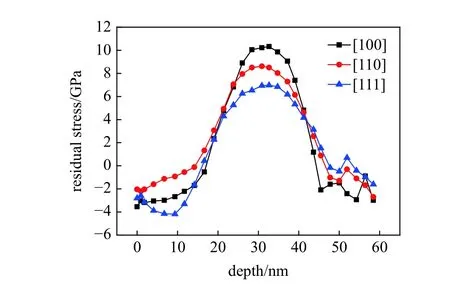
图14 残余应力 σxx 沿深度分布曲线Fig.14 The enolution curves of residual stress σxx with the depth

分析卸载之后位错密度沿冲击深度分布情况如图15 所示.可以看出,卸载之后位错密度同样表现出沿深度先增加后减小的梯度分布情况.但是,由于冲击波的反复反射导致塑性变形中缺陷的动态回复,造成了卸载后的位错密度大小较冲击过程中的有所减小.此外,由于[110]方向下产生了较多的无序结构,造成位错在无序结构处钉扎,使冲击波反射后位错的反向运动受阻,以至于位错动态回复更难发生,导致卸载之后[110]方向下的位错密度略大于[111]方向下的位错密度.

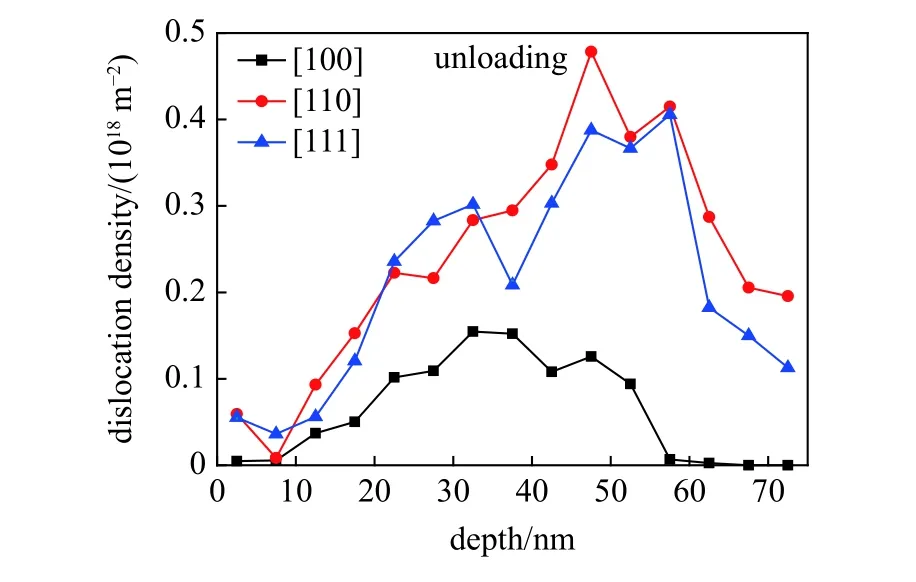
图15 卸载后位错密度分布Fig.15 Dislocation density distribution after unloading

激光冲击强化会产生梯度位错密度、梯度残余应力以及梯度晶粒尺寸3 种梯度结构.梯度位错密度可以使材料强度得到有效提高[47-49];梯度晶粒尺寸可以保持材料的应变强化能力[50-53]梯度残余应力可以降低疲劳裂纹的发生几率和抑制裂纹的扩展,从而延长零件的服役寿命[45,54-55].但限于分子动力学模拟的尺寸限制,在这里无法获得晶粒细化的模拟结果.以上研究成果可对分析实际工程中的冲击波传播特性和冲击波对材料的加工应用进行理论指导.

3 结论

基于Atomsk 和Lammps 软件对CoCrFeMnNi高熵合金进行了激光冲击的模拟,研究了不同冲击方向下冲击过程中的冲击波的传播特性、局部应力的分布情况、微观结构的变化以及冲击后的残余应力和位错密度分布情况,并将CoCrFeMnNi 高熵合金冲击过程微结构演化与纯Ni 进行对比,获得以下主要结论.

(1) 激光冲击强化诱导的弹塑性双波分离现象表现出了明显的取向效应.[100]方向拥有更多的可动滑移系,在沿[100]方向进行冲击时,滑移更容易发生,塑性变形更容易.这导致了在[100]冲击方向下塑性波传播速度变快,从而未出现双波结构.而沿[110]和[111]方向进行冲击加载时,可动滑移系较少,其塑性变形也更困难,进而导致了弹、塑性双波分离的现象.

(2) 沿[100]方向进行冲击时产生了BCC 中间相,中间相在后续的塑性变形过程中演变为FCC 结构、层错与少量的无序结构.在沿[110]以及[111]方向进行冲击时会产生大量的无序结构,这是由于高密度位错以及位错芯区域原子错排,使得原子排列呈无序化.

(3) CoCrFeMnNi 高熵合金由于晶格畸变效应使得位错更容易形核,导致在冲击过程中产生了较纯Ni 更高的位错密度以及更多的无序结构.

(4) 由于冲击波产生的塑性变形不均匀,导致在卸载后模型两端产生残余压应力,芯部产生残余拉应力.并且,卸载之后的位错密度同样呈现沿深度先增加后减小的梯度分布情况.