基于非常规平衡电抗器的直流侧 谐波抑制方法
2021-10-11廉玉欣杨世彦
廉玉欣 杨世彦 杨 威
(哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001)
0 引言
多脉波整流器具有可靠性高、实现简单、电磁兼容性好、谐波抑制效果显著等优点,广泛应用于高压直流输电、电化学加工、飞机变流系统等领域[1-4]。在多脉波整流器中,整流脉波数决定着系统的谐波抑制能力。近年来,提高整流脉波数已经成为国内外多脉波整流技术研究的热点,可分为三种方法:
(1)增加移相变压器的输出相数,进而同时增加输入线电流的阶梯数和输出负载电压的脉波数,以提升谐波抑制能力[5-8]。然而,随着输出相数的增加,移相变压器的结构、设计和工艺越来越复杂,很难保证对称性。
(2)采用多抽头式平衡电抗器,并通过优化设计抽头位置和参数,能够提高脉波数[9-10]。由于与抽头连接的附加二极管或开关管的电流总和与负载电流相同,随着抽头数量增加,导通损耗严重[11]。
(3)在多脉波整流器的直流侧安装无源或有源辅助电路。以消除输入线电流的谐波为目标,有源辅助电路产生具有特殊形状的电流波形,进而调节三相整流桥的输出电流[12-14]。
尽管有源辅助电路是抑制电流谐波的有效方法,但是实现方案相对复杂,而且不能增加负载电压的脉波数。文献[15]改变传统平衡电抗器(Interphase Reactor, IPR)结构,通过IPR二次绕组连接无源辅助电路,并联到负载两端。无源辅助电路可采用单相全波整流电路或单相全桥整流电路,能够同时增加输入电流的阶梯数和负载电压脉波数,且采用不控二极管实现、方法简单[16-19]。
综合上述方法,无论是采用多抽头式平衡电抗 器还是直流侧辅助电路的方法,都改变了传统平衡电抗器的结构。本文针对并联型多脉波整流器,提出了基于非常规平衡电抗器(Unconventional Interphase Reactor, UIPR)的直流侧谐波抑制方法。UIPR具有一次绕组和二次绕组,一次绕组按照抽头式平衡电抗器的方式工作,作为第一级谐波抑制方法;二次绕组与二次侧整流电路相连,可增加整流系统的输出模式,从而增加整流器输入线电流的阶梯数和输出负载电压的脉波数,作为第二级谐波抑制方法。UIPR的一次侧抽头数量,直接影响其工作模式和控制方式,使得整流器直流侧谐波抑制方法并不相同。本文研究了UIPR的基本结构、工作模式、最优设计以及直流侧谐波抑制机理,理论分析和实验结果表明,基于UIPR的直流侧无源谐波抑制方法对整流器输入电流谐波具有显著的抑制效果。
1 具有UIPR的并联型多脉波整流器及其工作模式分析
1.1 具有UIPR的并联型多脉波整流器拓扑分析
具有非常规平衡电抗器的并联型多脉波整流器如图1所示,由移相变压器、两组三相整流桥RECⅠ和RECⅡ、零序电流抑制器(Zero Sequence current Blocking Transformer, ZSBT)、UIPR、一次侧抽头控制电路和二次侧整流电路组成。UIPR二次绕组连接的整流电路并联在负载两端,当二次侧整流电路正常工作时,能够增加整流系统输出电压的脉波数,同时增加输入电流的阶梯数,并降低输入电流总谐波畸变率(Total Harmonic Distortion, THD),属于直流侧谐波抑制方法。
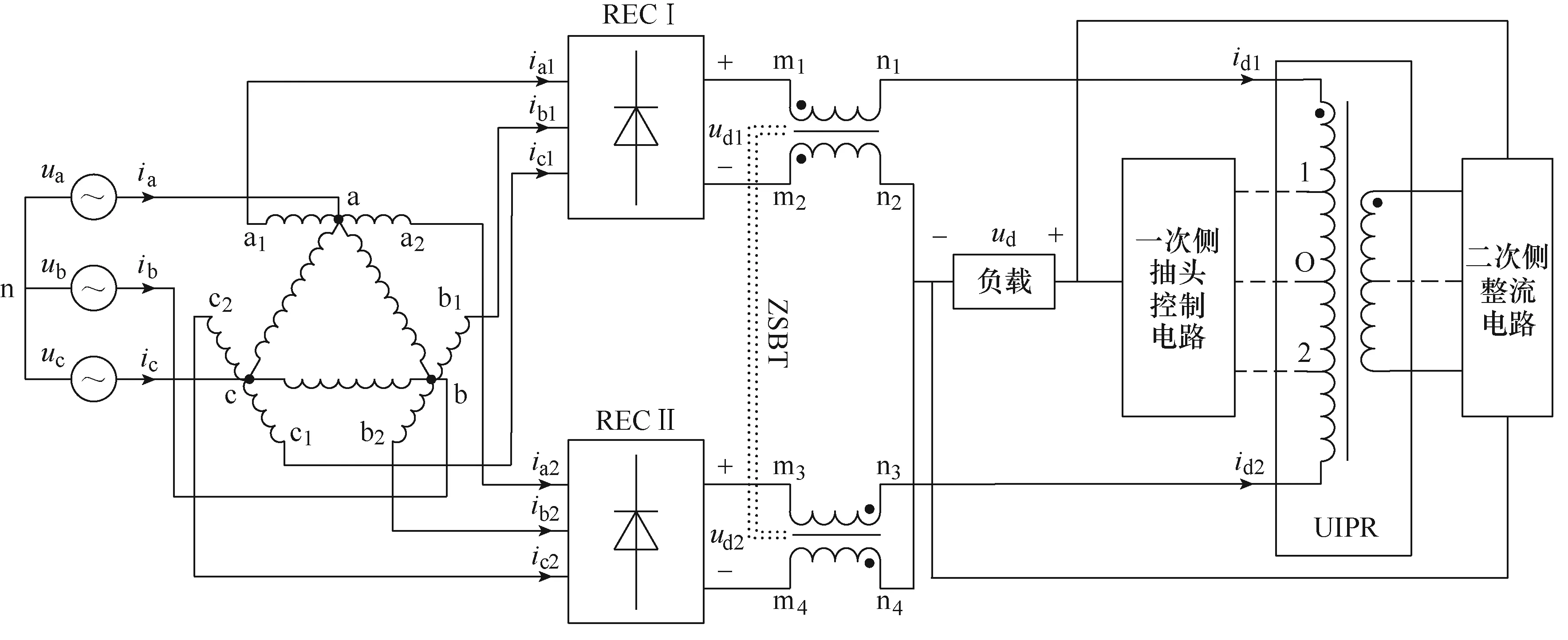
图1 具有非常规平衡电抗器的并联型多脉波整流器 Fig.1 Parallel-connected multipulse rectifier with UIPR
为了能够消除整流器输入电流中的5、7次谐 波,移相变压器需要给整流桥提供两组相差30°的三相电压。本文采用主绕组为三角形联结的自耦式移相变压器,其两组三相输出电压与网侧供电输入相电压之间的相位差为±15°[20]。当三角形联结自耦变压器等效容量最小且结构最为简单时,三角形联结自耦变压器的绕组结构与相量如图2所示[21]。图中, 相位差ϕ=15°,其匝比需满足,、和为网侧自耦变压器输入相电压,、和为自耦变压器一组输出相电压,、和为自耦变压器另一组输出相电压,、和为自耦变压器输入线电压。
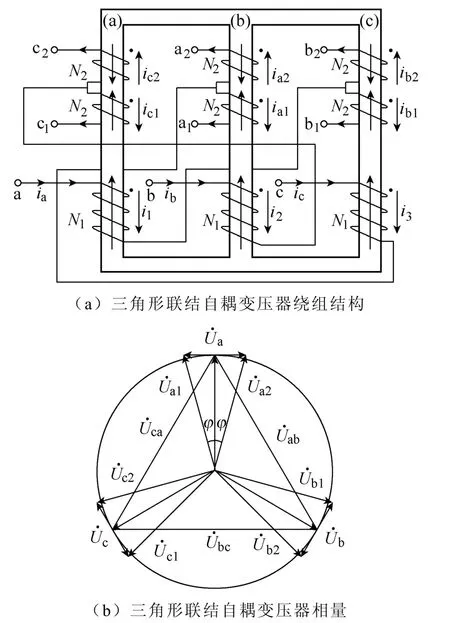
图2 三角形联结自耦变压器的绕组结构与相量 Fig.2 Winding configuration and phase diagram of delta-connected autotransformer
UIPR的抽头位置与绕组结构如图3所示。假定T和T′为UIPR的一次绕组抽头点,OT或OT′间的绕组匝数与一次绕组总匝数之比为α,UIPR二次绕组总匝数Ns与一次绕组总匝数Np的匝比为m。根据一次侧抽头数量,UIPR的基本结构可分为单抽头、两抽头和多抽头等形式。根据结构最优的原则,二次侧整流电路可采用单相全波整流电路或单相全桥整流电路。
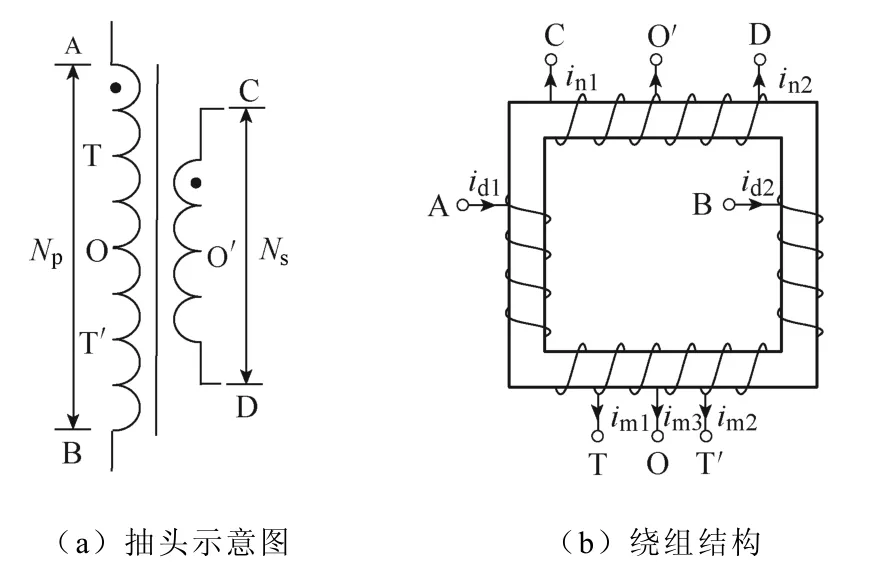
图3 UIPR的抽头位置与绕组结构 Fig.3 Tap structure and winding configuration of UIPR

图4 UIPR谐波抑制电路 Fig.4 Harmonic reduction circuit with UIPR
UIPR的二次绕组是否引出中心抽头取决于二次侧整流电路的结构,当二次侧连接单相全波整流电路时,需要引出中心抽头,当二次侧连接单相全桥整流电路时,则不需要引出中心抽头。图4所示 为一次侧中心抽头、两抽头和三抽头形式的UIPR谐波抑制电路。当一次侧抽头数量小于3时,谐波抑制电路均为无源器件,抽头数量大于等于3时,需要引入控制电路以实现开关管的导通时序。通过合理选择图4所示的UIPR参数,可使得整流器分别工作在24、36、48脉波整流状态。
1.2 UIPR工作模式分析
假定图1中的负载为大电感阻感类负载,负载电流可视作恒定值Id。假设整流器输入电压为
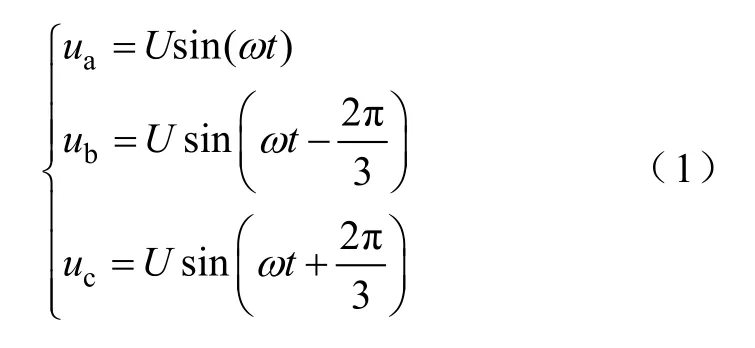
式中,U为整流器输入相电压的幅值。
UIPR的工作模式与一次侧抽头的数量n、二次电压us、负载电压ud以及三相整流桥输出电压ud1和ud2有关。二次侧整流电路可以在UIPR一次侧抽头基础上,增加两种工作模式。因此,UIPR具有n+2种工作模式。以图4c为例,分析一次侧三抽头UIPR工作模式,如图5所示。
1)工作模式Ⅰ


图5 工作模式 Fig.5 Operation modes

2)工作模式Ⅱ

3)工作模式Ⅲ
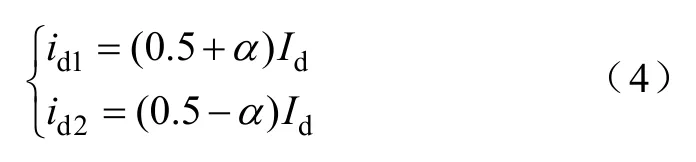
4)工作模式Ⅳ
当−us>ud和ud1<ud2,且一次侧开关管Q1关断、Q2导通时,此时UIPR工作模式如图5d所示。二次侧单相全桥整流电路的二极管VD22和VD23导通,VD21和VD24不导通。一次侧二极管VD12导通,VD13和VD11关断。此时,由于负载电压ud大于第一组三相整流桥(REC Ⅰ)的输出电压ud1,使得电流id1=0,因此可以得出
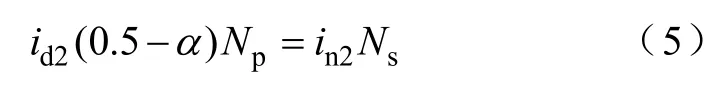
根据基尔霍夫电流定律(KCL),以及UIPR匝比m和抽头位置的定义,可以得出
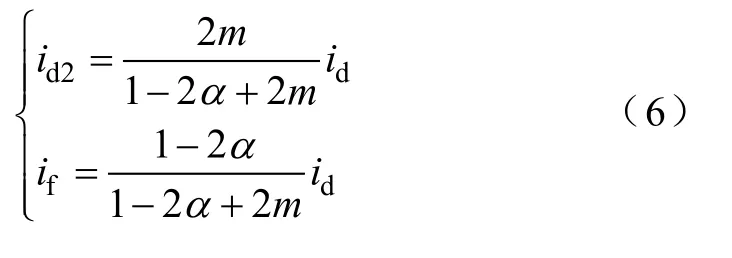
5)工作模式Ⅴ
当us>ud和ud1>ud2,且一次侧开关管Q1导通、Q2关断时,此时UIPR工作模式如图5e所示。二次侧单相全桥整流电路的二极管VD21和VD24导通,VD22和VD23不导通。一次侧二极管VD11导通,VD13和VD12关断。此时,由于负载电压ud大于第二组三相整流桥(RECⅡ)的输出电压ud2,使得电流id2=0,因此可以得出
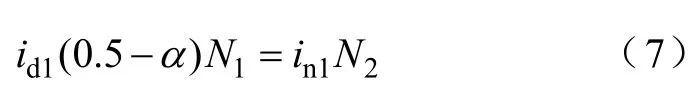
分析过程与模式Ⅳ类似,可以得到
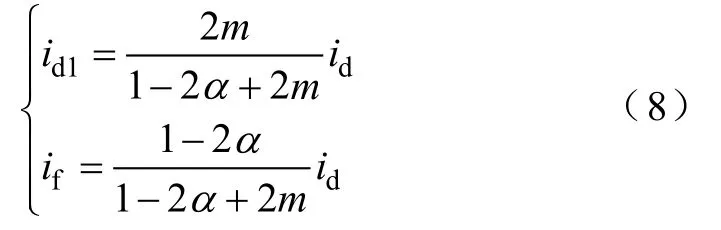
2 UIPR的优化设计
2.1 UIPR的工作条件
根据图2,三角形联结自耦变压器的输出电压可以表示为

根据三相全桥整流调制理论,两组三相整流桥REC Ⅰ和REC Ⅱ的输出电压分别表示为
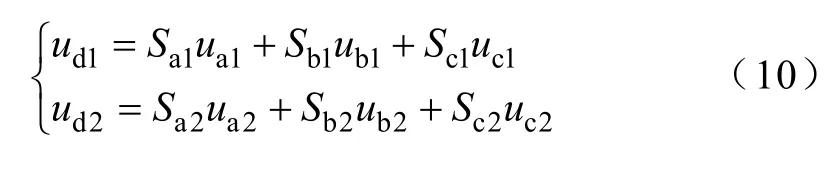
式中,Sa1、Sb1、Sc1、Sa2、Sb2和Sc2为每一相的开关函数,Sa1可以表示为
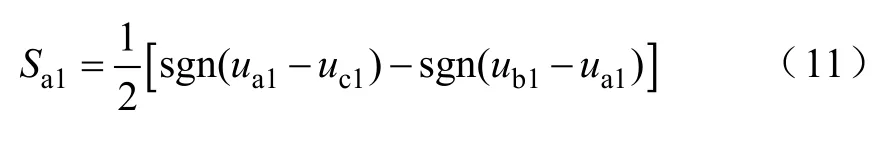
其他开关函数之间的关系为

因此,输出电压ud1和ud2可分别表示为

式中,k=0, …, 5。
如图1和图3所示,UIPR一次绕组端电压up=ud1−ud2,因此,可得UIPR二次绕组端电压us为
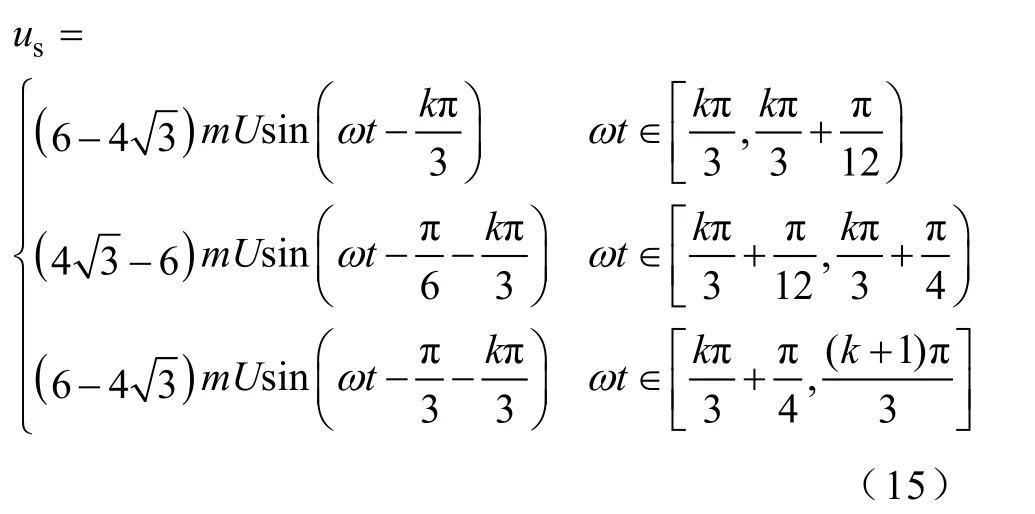
由式(15),可得到电压us绝对值的最大值为

根据图4可知,若使二次侧整流电路工作,需满足

式中,udmin为UIPR工作在传统抽头变换器时,整流器负载电压的最小值。
根据图4和图5,可以得到最小负载电压为

由式(16)~式(18)可得

即UIPR的匝比m和一次侧抽头匝比α满足上述必要条件时,UIPR的二次侧整流电路可以工作。
2.2 UIPR的匝比优化设计
上述必要条件并不能保证整流器工作在期望的脉波数和最佳谐波抑制效果。因此,需要以整流器输入线电流的THD最小值为目标,进一步优化设计UIPR。
由图1和图2,根据安匝平衡原理和基尔霍夫电流定律,可得整流器输入线电流为

式中,三相整流桥输出电流id1和id2的周期均为π/3,幅值与UIPR的工作模式有关。图5中,UIPR具有五种工作模式,因此id1和id2在一个周期内具有五种幅值。同理,两抽头UIPR时,为四种;中心抽头时,为三种。根据图5,可得电流id1和id2的表达式,见附录。
定义电流的有效值为

式中,i为电流的瞬时值;T为电流的周期。
a相输入线电流THD满足

式中,Ia为电流ia的有效值;I1为基波电流有效值。
具有三抽头UIPR的整流器工作在48脉波整流状态,输入线电流波形中应包含48个等宽度的阶梯。因此,开关管Q2初始导通角为π/48。当初始导通角为π/16时,二次侧单相全桥整流电路输出电压等于负载电压。UIPR的匝比m和一次侧抽头匝比α满足
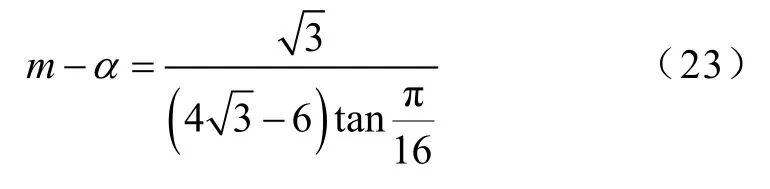
根据式(21)、式(23)和附录中a相输入线电流的表达式,可得Ia为
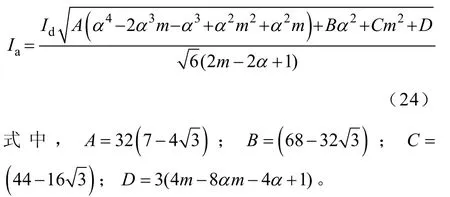
利用傅里叶级数,同样可以得到基波电流有效值。进一步通过式(22),可得THD表达式,并对其求导得到,当α=0.245 7,m=9.627时,THD最小值为3.81%。输入线电流THD与α和m的关系曲线如图6所示。

图6 THD与α 和m的关系曲线 Fig.6 Relation curves among THD, α and m
2.3 UIPR的容量分析
以一次侧三抽头UIPR为例,在最优参数条件下,整流器工作在48脉波整流状态。根据UIPR的工作模式,可知UIPR一次绕组端电压有效值为

由图3可知,UIPR的一次绕组由4段小绕组组成,流经绕组AT和BT′的电流等于id1和id2,其有效值为

根据UIPR的工作模式,以及三相整流桥输出电流id1和id2的表达式,可求得一次绕组TT′段流经电流的有效值为

UIPR二次绕组端电压有效值为

UIPR二次绕组流经电流的有效值为

因此,一次侧三抽头UIPR的容量为

按照上述方法,可以得到一次侧不同抽头数量时,UIPR最优参数、容量以及输入线电流THD,见表1。

表1 不同一次侧抽头数量时,UIPR的最优参数 Tab.1 The optimal parameters of UIPR with different numbers of primary tap
3 仿真与实验验证
为验证理论分析的正确性,根据图1所示的多脉波整流器电路拓扑,利用PLECS软件进行仿真验证,同时设计并研制了一台3kW的并联型多脉波整流器。UIPR参数和仿真实验条件如下:输入相电压为120V,频率为50Hz,阻感负载为30Ω 和10mH,不同类型UIPR的匝比参数见表1。
具有不同UIPR拓扑的整流器a相输入线电流仿真结果如图7所示,其频谱仿真结果如图8所示。具有常规IPR的整流器输入线电流为12阶梯波,随着UIPR一次侧抽头数的增加,输入线电流的阶梯数增加到24、36、48脉波,波形趋于正弦波,电流谐波成分逐渐减少。


图7 输入线电流仿真结果 Fig.7 Simulation results of input line current
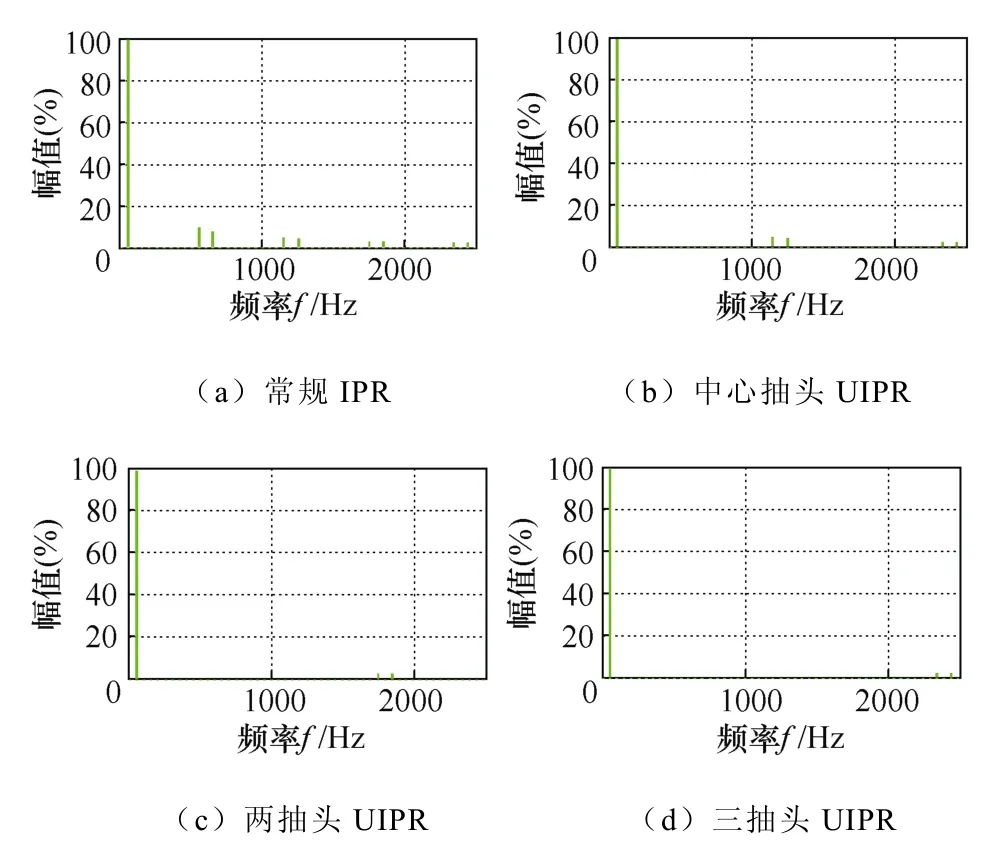
图8 输入线电流频谱仿真结果 Fig.8 Simulation results of spectrum of input line current
图9为具有不同UIPR拓扑的整流器输入线电流及其频谱的实验结果。输入线电流THD的仿真结果和实验结果误差分析,见表2。具有常规IPR的整流器输入线电流的THD=12.23%,略低于理论THD值15.15%。由图9b~图9d的实验结果可知,随着UIPR一次侧抽头数的增加,输入线电流的波形趋于正弦波,THD测试结果随之减小,绝对误差和相对误差也相应的减小,因此采用UIPR具有显 著的谐波抑制效果。图9和表2所示的THD测试结果均略低于理论值,这是由于自耦变压器和平衡电抗器的漏感影响而造成的,而且随着UIPR一次侧抽头数的增加,对测试结果的影响越来越小。


图9 输入线电流及其频谱 Fig.9 Input line current and its spectrum
图10所示为三相整流桥(REC Ⅰ和REC Ⅱ)输出电流。UIPR的引入,改变了电流id1和id2的形状,随着UIPR一次侧抽头数量的增加,三相整流桥输出电流依次变为4、6、8阶梯波。

表2 输入线电流THD的仿真结果与测试结果 Tab.2 Simulation and experimental THD results of input line current
图11所示为三相整流桥(REC Ⅰ和REC Ⅱ)输出电压,UIPR的引入使得输出电压的每个谷底处均有微小的突起。随着UIPR一次侧抽头数量的增加,不会改变三相整流桥输出电压ud1和ud2的整体形状。


图10 三相整流桥输出电流 Fig.10 Output current of three-phase diode-bridge rectifier
图12所示为负载纹波电压。使用常规IPR时,负载电压在一个电源周期内具有12个脉波。采用UIPR后,负载电压脉波数依次增加到24、36、48 脉波。实验测试时,由于整流器中电感的滤波作用,负载纹波电压波形较为平滑。

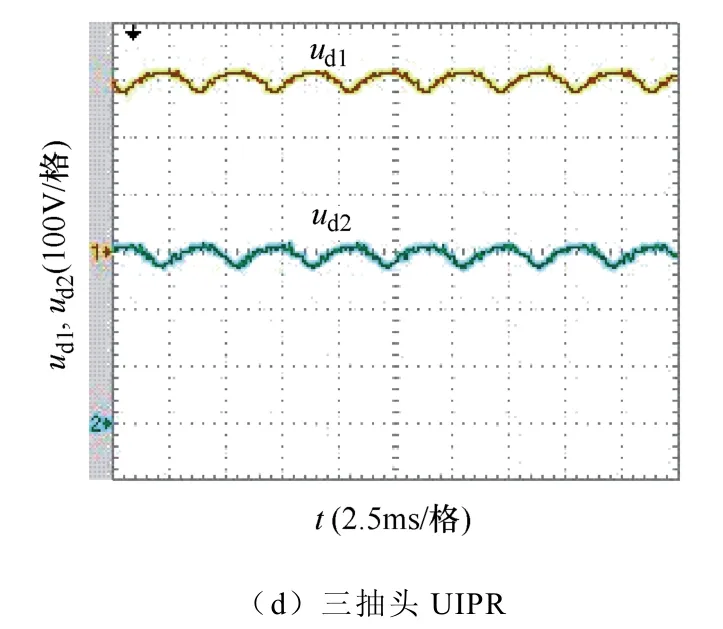
图11 三相整流桥输出电压 Fig.11 Output voltage of three-phase diode-bridge rectifier


图12 负载纹波电压 Fig.12 Load ripple voltage
4 结论
本文提出了一种基于UIPR的直流侧谐波抑制方法,并应用于全桥并联型多脉波整流器。UIPR增加了一次侧抽头数和二次绕组,并经过一次侧抽头控制电路和二次侧整流电路与负载相连。通过优化设计UIPR的一次侧抽头匝比和电压比,使整流器输出电压脉波数从12脉波增加至24、36、48脉波,输入线电流波形近似正弦化,其THD由15.15%降低至7.52%、5.04%、3.81%。仿真和实验结果验证了理论分析的正确性,且方法简单、易于实现,多脉波整流器的电流谐波抑制效果显著提高。
附 录
三相整流桥输出电流id1和id2的周期均为π/3,幅值与UIPR的工作模式有关。根据图5,可得电流id1和id2的表达式为


定义开关管Q2初始导通角为θ1,假设二次侧单相全桥整流电路开始工作的初始导通角为θ2。将电流id1和id2的表达式代入式(20),可得整流器输入线电流的表达式为

为简化分析,仅分析a相输入线电流。
