基于行为距离的带隐变迁过程模型挖掘方法
2021-10-11王丽丽方贤文
王丽丽,方贤文
(1.安徽理工大学 数学与大数据学院,安徽 淮南 232001;2.同济大学 嵌入式系统与服务计算教育部重点实验室,上海 201804)
0 引言
过程挖掘的目标是从事件日志中自动发现有价值的信息,从而监控并指导增强业务过程管理[1]。在过程挖掘中存在很多问题,如短循环、复制变迁、不可见变迁、非自由选择结构、噪音、低频行为、不完备性等,其中不可见变迁又称为隐变迁,本文重点研究隐变迁的挖掘方法。现实生活中由于各种因素可能导致过程模型中存在隐变迁,它们主要起到路由的目的,隐变迁之所以难以挖掘是因为它不出现在事件日志的任何迹中。其中隐变迁出现的主要原因有以下几种[2]:
(1)在过程模型中存在没有实际意义仅用于路由目的任务;
(2)某些实际任务在某些事件迹中可以被缺失执行;
(3)用于过程模型增强服务,允许存在跳过、重做当前任务或跳转到任意的先前任务,但是这些执行逻辑在过程模型的控制流中没有被表达出来。
目前已存在一些隐变迁的挖掘方法,如α# 算法[2-3],α$[4],IM(inductive mining)方法[5],耦合隐马尔可夫模型-不可见任务 (Coupled Hidden Markov Model-Invisible Task,CHMM-IT)[6],耦合隐马尔可夫模型-非自有选择的不可见任务(Coupled Hidden Markov Model-Nonfree Choice Invisible Task,CHMM-NCIT)[7]等。文献[3]在文献[2]的基础上提出了带基本不可见任务的过程模型的挖掘方法,但是无法解决并发结构中的隐变迁问题。文献[4]提出了α$算法,讨论了非自由选择网中的隐变迁的挖掘问题,但是仍然不能发现并发结构中的隐变迁。IM方法[5]通过流程树切实现了带隐变迁的过程模型挖掘,但是该方法发现的过程模型中存在大量的冗余变迁,导致过程模型非常复杂。文献[6-7]采用隐马尔可夫的方法给出了自由和非自由选择网在日志不完备情况下的隐变迁挖掘方法,其中CHMM-NCIT和CHMM-IT都使用了耦合隐马尔可夫模型(CHMM),同时利用Baum-Welch算法来决定CHMM的变量权重,然而这些算法的时间复杂度非常高,实现起来较困难。文献[8]提出一个优于MINERful算法的方法,该方法能够构建一个带有不可见任务的声明式模型和非自由选择的命令式模型中的不可见任务,但是其中控制流通过声明模型中的组合规则建立,没有明确的不可见任务输出。文献[9]提出一个基于图的算法,但是当事件日志较大时,数据库图很难表达事件之间的依赖关系。综上所述,本文提出一种基于行为距离发现隐变迁的新方法,主要工作如下:
(1)提出了行为距离的概念,量化了日志或模型中活动对之间的发生依赖关系。
(2)通过日志基本行为关系对日志中的活动对间的行为关系进行了定性分析,进一步细化了传统的行为轮廓。
(3)从行为的角度给出了带隐变迁的过程模型挖掘方法,该方法能发现多种类型的隐变迁,解决并发结构中隐变迁发现困难的问题,而且不会产生大量的冗余隐变迁。
1 动机例子
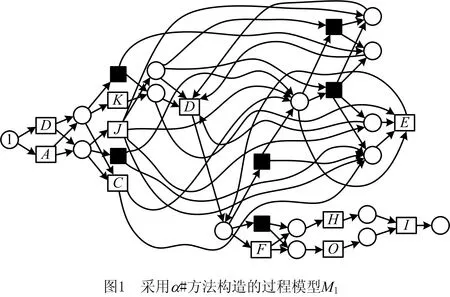
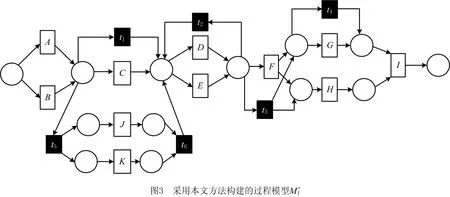
由于隐变迁不出现在任何事件日志中,有效地挖掘所有的隐变迁是过程挖掘的一个具有挑战性的问题。下面通过实例说明目前技术在隐变迁挖掘方面存在的问题。对于事件日志L1={σ1,σ2,σ3,σ4,σ5,σ6,σ7,σ8,σ9,σ10,σ11},其中:σ1=ACDDFGHI,σ2=BCDEEFHGI,σ3=ADEDEGHI,σ4=AEDGHI,σ5=BEDHGI,σ6=BDEHGI,σ7=BCEDFHI,σ8=AJKDEFGHI,σ9=BJKDHGI,σ10=AKJEEDFHGI,σ11=BKJDEDDEGHI,在不考虑迹的频度的前提下,分别采用文献[3]和文献[5]提出的挖掘算法得到如图1和图2所示的过程模型,采用本文方法得到的过程模型如图3所示。显然,文献[3]无法发现没有直接跟从关系的活动对间的隐变迁,如图1中活动F和活动I之间的隐变迁,而且模型非常复杂。对于IM方法[5]产生了大量的冗余隐变迁,从而导致如图2所示的模型变得非常复杂。针对上述问题,本文提出一个基于日志行为关系和行为矩阵的带有无冗余隐变迁的过程模型发现方法,并通过一组实验验证了该方法的有效性,解决了目前在隐变迁挖掘上存在的问题。

2 基本概念
关于Petri网的基本定义和相关知识请参见文献[10],标签Petri网相关知识请参见文献[11],本章只给出与本文相关的核心定义。Petri网的变迁用来表示动作,通常可以分为可见变迁和不可见变迁(又称为隐变迁),它们分别描述具有明确含义的动作和没有明确解释的动作。假设A表示变迁所代表的有明确含义的所有动作标签;τ表示特殊的标签,其中τ∉A;T是一些列活动集合。
定义1[11]标签Petri网。一个标签Petri网是一个四元组N:=(P,T,F,λ),其中:(P,T,F)是一个Petri网,λ:T→A∪{τ}是一个将标签分配给变迁的函数。如果λ(t)≠τ,则t是可见的,否则t是不可见或沉默的。
定义2[11]执行序列(或出现序列)。设S:=(N,M0)是一个标签网系统,其中N:=(P,T,F,λ)。网系统S的所有带标签的执行序列是所有遵循网系统S的可执行语义的形如{ai}·(Aτ)*·{af}组成的序列集合,其中ai,af分别是人工添加的开始变迁和结束变迁。记网系统S的所有带标签的执行序列为T(S)。
定义3[12]直接跟从关系(日志)。设L是活动T上事件日志。设a,b∈T,若存在一条迹σ=t1t2…tn使得σ∈L,且ti=a,ti+1=b(其中i∈{1,2,…..,n-1}),则称活动a和活动b之间存在直接跟从关系,记为a>Lb。
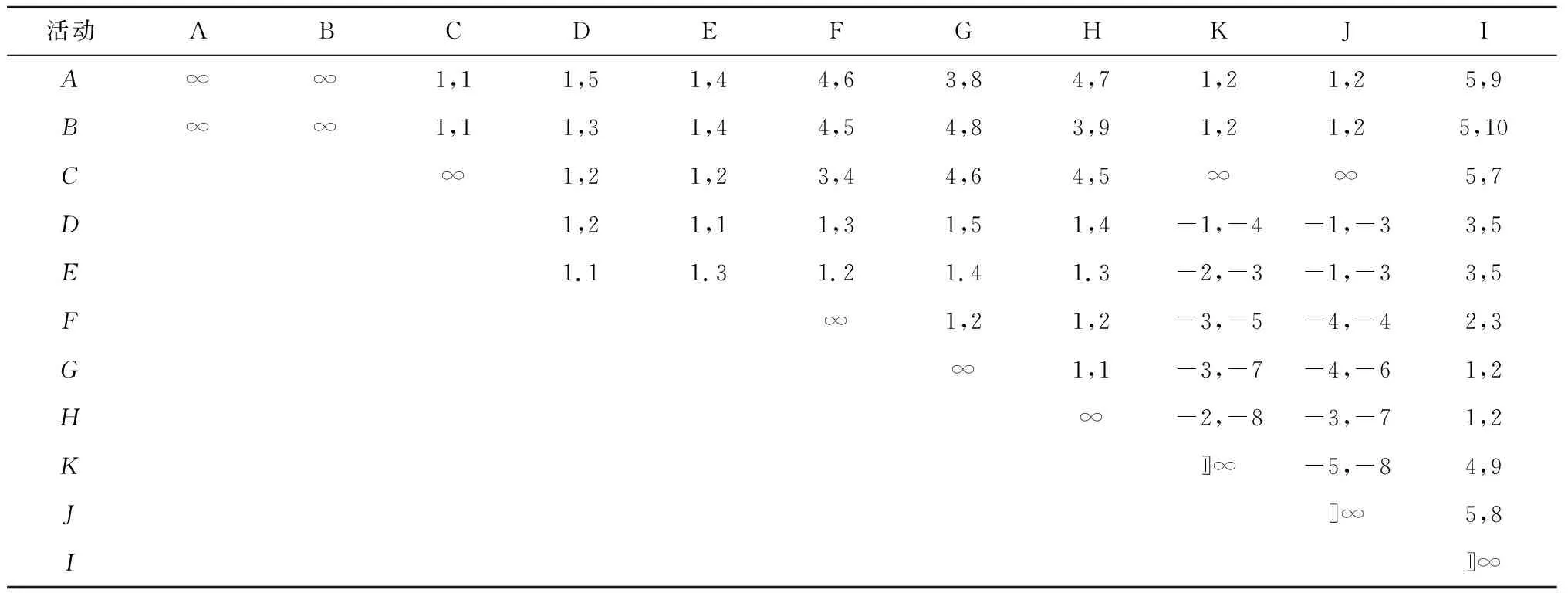
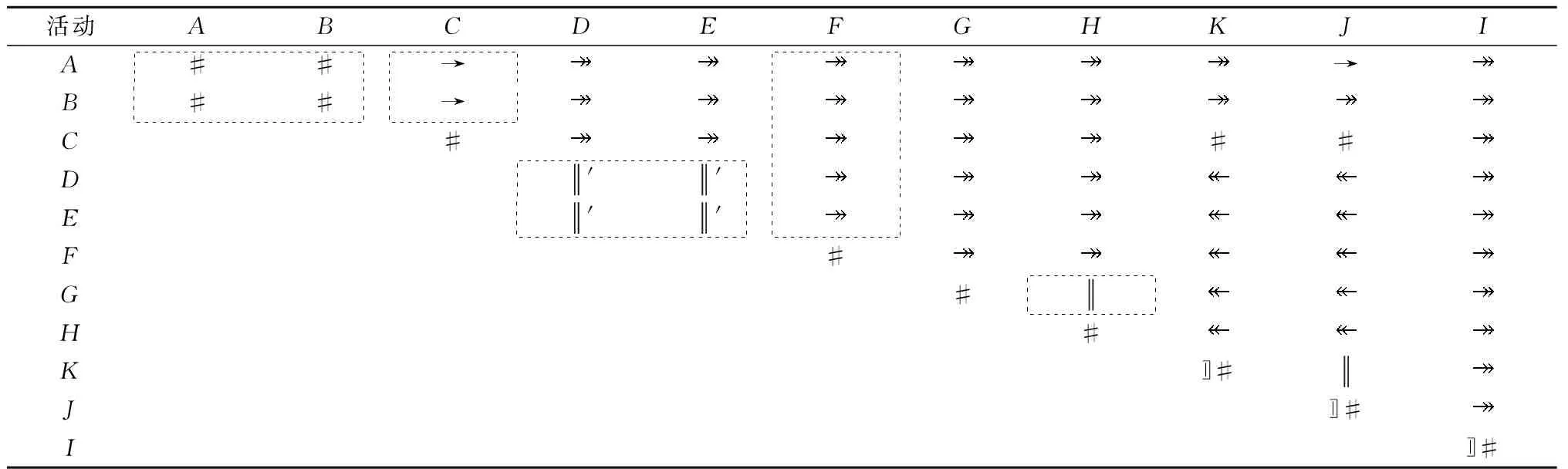
定义4[12]弱序关系(日志)。设L是活动T上事件日志。设a,b∈T,若存在一条迹σ=t1t2…tn使得σ∈L,且ti=a,tj=b(其中1≤i 本章给出了发现and网关类型和循环类型隐变迁的方法,并通过算法说明了如何根据日志的行为特征关系和行为距离构建带and网关类型和循环类型的隐变迁的初始过程模型。 定义5基于迹的行为距离。设L是活动T上事件日志,a,b∈T,对于一条迹σ∈L,活动a和活动b之间的行为距离定义为: (1) 在定义5的基础上,定义6给出了基于日志的活动间最大行为距离和最小行为距离。 定义6基于日志的最大行为距离和最小行为距离。设L是活动T上事件日志,设a,b∈T,对于日志L,活动a和活动b基于日志的最大行为距离BDismax(a,b,L)和基于日志的最小行为距离BDismin(a,b,L)分别定义为: (2) 若活动a和活动b处于排他序关系,显然它们不可能同时出现在任何迹中,则BDismin(a,b,L)=BDismax(a,b,L)=∞。若在任意迹中满足aLb且bLa,则BDismin(b,a,L)=-BDismin(a,b,L)。 对于事件日志L,AL代表出现在日志L中的所有活动集合,设|AL|=n,则日志的行为距离矩阵BDisMatrix是n×n维的矩阵,∀a,b∈AL,活动a和活动b间的行为距离等于矩阵中活动a所在的行和活动b所在列对应的值Ma,b=x,y,其中x=BDismin(a,b,L),y=BDismax(a,b,L)。表1给出了第1章日志L1中各活动对的行为距离矩阵。 表1 日志L1中活动对间的行为距离矩阵 定义7将文献[3]中的虚假依赖关系从因果依赖关系中剔除出去,给出了基于日志的基本行为关系,细化了传统的行为轮廓。 定义7基于日志的基本行为关系。设L是活动T上事件日志,设a,b∈T: (1)因果依赖关系→L,当且仅当a>Lb且b≯La,且BDismin(a,b,L)=BDismax(a,b,L)=1; 对于第1章中的事件日志L1,根据定义7得到活动间的基本行为关系如表2所示。 表2 基于日志L1的基本行为关系矩阵 定义8隐变迁类型。设N:=(P,T,F,λ)是一个标签Petri网,A∪τ表示所有活动标签,对t1,t2,t∈A∪τ,若满足: (5)λ(t)=τ,·t={s},·s=∅,|t·|>1或t·={s},s·=∅,|·t|>1,则称t为side类型的隐变迁。 图4给出了side类型、skip类型、loop类型、switch类型、and网关类型隐变迁的示例。 根据网系统的结构特征,引理1和定理1分别给出了网关隐变迁和循环隐变迁的挖掘方法。 引理1对处于并发交叉序关系的活动,默认存在and-split 和and-join隐变迁。 引理1可能导致冗余的网关隐变迁,在算法1中,将根据隐变迁和其前置或后置变迁的结构关系,对冗余网关隐变迁进行删除。 定理1设L是活动T上事件日志,若T′⊂T是满足循环交叉序关系的极大活动子集,且∀t∈T′均属于loop-body部分变迁,则一定存在循环类型隐变迁作为loop-redo变迁。 证明采用反证法。若不存在循环类型的隐变迁,即存在一个可见变迁t′∈T作为loop-redo变迁。由于∀t∈T′均属于loop-body部分变迁,T′中的活动结构属于命题5中的3种情况之一,这里不再详细讨论。T′与t′的可能网结构如图5所示,易知,∀t∈T′与t′满足循环交叉序关系,故满足循环交叉序关系的极大活动子集为T′∪t′,矛盾。故定理1成立。证毕。 由于边界隐变迁挖掘比较简单,本文不讨论边界类型的隐变迁挖掘的方法。算法1首先根据事件日志L建立活动对之间的行为距离矩阵和行为关系矩阵,在此基础上构建若干个子模块,同时采用引理1和定理1发现and网关类型和循环类型的隐变迁。最后,将这些子模块组合成一个Petri网模型,同时删除其中冗余的and网关类型的隐变迁。 算法1发现带网关类型和loop类型的沉默变迁的Petri网模型M0。 输入: 事件日志L; 输出: 初始的Petri网模型M0。 1.根据日志L建立活动间的行为距离矩阵BDisMatrixn×n; 2.根据日志L建立活动间的行为关系矩阵BRelMatrix; 3.If活动集S和活动集T处于排他序关系, 4.then活动集S和活动集T处于结构排他关系,构造由S和T组成排他结构。 5.If活动集S和活动集T处于并发交叉序关系, 6.then活动集S和活动集T处于结构并发关系,构造由S、T、and-split和and-join隐变迁组成的并发结构。 7.If活动集S和活动集T处于循环交叉序关系, 9.if BDis(a,s′,L)min≥BDis(a,t′,L)min+1,且对于T′=S∪T ∀σ∈L,|OccurTime(s′,σT′)-OccurTime(t′,σT′)|≤1, 10.then活动集S和活动集T处于顺序结构中的循环交叉。 11.if BDis(a,s′,L)min=BDis(a,t′,L)min=1,且对于∀σ∈L,OccurTime(s′,σT′)与OccurTime(t′,σT′)无依赖关系, 12.then活动集S和活动集T处于排他结构中的循环交叉。 13.if BDis(a,s′,L)min=BDis(b,t′,L)min=1,BDis(a,s′,L)max=BDis(a,t′,L)max=2,且对于∀σ∈L,OccurTime(s′,σT′)=OccurTime(t′,σT′), 14.then活动集S和活动集T处于并发结构中的循环交叉。 15.if活动集S和活动集T都属于循环体(loop-body)部分, 16.then添加循环类型的隐变迁t(其中λ(t)=τ)作为循环重做(loop-redo) 17.while(存在未组合的块)do, 18.遍历BRelMatrix中的因果依赖关系,通过因果依赖关系将块结构组合在一起, 19.遍历BRelMatrix中的严格序关系,将剩余的块结构合为一个完整的Petri网模型, 20.for(所有的and-split和and-join类型的隐变迁检查是否冗余)设l(t)=τ。 21.if t·>1且|·(·t)|=1,l(·(·t))≠τ, 22.then删除and-split类型的隐变迁t,并用·(·t)变迁替换t。 23.if·t>1且|(t·)·|=1,l((t·)·)≠τ, 24.then删除and-join类型的隐变迁t,并用(t·)·变迁替换t。 25.得到带有无冗余的网关类型和循环类型隐变迁的初始Petri网模型。 下面利用算法1对第1章中的事件日志L1构建初始Petri网模型。行为距离矩阵和基本行为关系矩阵如第1章中表1和表2所示。根据步骤3~步骤16构造出如图6所示的4个子模块,利用步骤17~步骤19将图6所示的4个子结构组合为一个完整的过程模型如图7所示。 最后,根据步骤20~步骤25删除图7中冗余的and网关类型的隐变迁t2和t3,得到带有无冗余的and网关类型和循环类型隐变迁的初始过程模型M0如图8所示。 本章将讨论如何在算法1构建的初始过程模型的基础上挖掘skip类型的隐变迁,从而进一步优化初始过程模型。下面首先给出相关定义。 定义9基于模型的最小行为距离。设S=(N,M0)是一个网系统,其中:N:=(P,T,F,λ)是一个标签Petri网,A∪τ表示所有的活动标签,a,b∈A,对于网系统S,活动a和活动b基于模型的最小行为距离BDismin(a,b,S)定义为: BDismin(a,b,S)={k|∀σ∈T(S),BDis(a,b,σ)≥k}。 (3) 定理2描述了通过比较两个活动在日志中的最小行为距离和其在模型中的最小行为距离的大小关系来挖掘skip类型隐变迁的方法。 定义10前置变迁集和后置变迁集。设S=(N,M0)是一个网系统,其中N:=(P,T,F,λ)是一个标签Petri网。∀t∈T,·(t)T={t′|t′∈T∧(t′)·∩·t≠∅},称·(t)T为t的前置变迁集。同理定义t的后置变迁集(t)·T。 定义11基于模型的并发结构最小行为距离。设S=(N,M0)是一个网系统,其中N:=(P,T,F,λ)是一个标签Petri网。t1,t2∈T,t1是and-split变迁,t2是and-join变迁,网系统S的所有可执行变迁序列集合记为T(s),t1和t2基于模型的并发结构最小行为距离 BDis‖min(t1,t2,S)={k|∀σ∈T(s)∧BDis(t1,t2,σ)≥k}。 (4) 某两个活动只要在日志的某条迹中存在直接跟从关系,利用定理2能发现位于它们之间的skip类型隐变迁。 定理2只能发现其中一类活动对之间的隐变迁,这些活动对在日志中至少存在一条迹使得它们之间有直接跟从关系,但是对于图3中的隐变迁t4是无法发现的。针对这种情况,定理3给出了并发结构中的隐变迁识别方法。 定理3设L是活动A上事件日志,S=(N,M0)是一个网系统,其中N:=(P,T,F,λ)是一个标签Petri网,A∪τ表示所有的活动标签。∀t1,t2∈T,其中t1为and-split变迁,t2为and-join变迁,①当λ(t1)≠τ,λ(t2)≠τ,如果BDismin(λ(t1),λ(t2),L) 证明不失一般性,这里仅给出最基本情况的并发结构作为示例证明定理的正确性。假设不存在skip类型的隐变迁。由于t1为and-split变迁,t2为and-join变迁,分两种情况进行讨论: (1)当t1和t2都是可见变迁时,可能的子结构如图9所示。∀σ∈T(S),若t1∈σ,则迹σ的形如…t1abt2…或…t1bat2…形式,易知BDismin(t1,t2,S)=3,若t1和t2的并发分支结构上不存在隐变迁,则BDismin(λ(t1),λ(t2),L)≥3。显然与BDismin(λ(t1),λ(t2),L) (2)当t1和t2都是隐变迁时,网结构如图10所示,∀σ∈T(s),如果a∈σ∨b∈σ,则可执行的变迁集为σ=…ct1abt2d…或σ=…ct1bat2d…,此时BDis‖min(t1,t2,S)=3,所以∀σ∈L,若∃σ∈L,a∈σ∨b∈σ则BDis(c,d,σ)≥3,所以,若t1和t2的并发分支结构上不存在隐变迁时,BDismin(c,d,σ) 算法2的基本思想是分析活动在日志中的最小行为距离和它们在模型中的最小行为距离之间的关系,通过定理2和定理3判断其间是否存在skip类型的隐变迁,其具体实现步骤如算法2所示。 算法2发现skip类型隐变迁,构建基于事件日志L的最终Petri网模型M1。 输入:事件日志L,初始Petri网模型M0,行为距离矩阵BDisMatrixn×n; 输出:基于事件日志L的Petri网模型M1。 1.遍历行为距离矩阵BDisMatrixn×n 2.while(存在BDismin(a,b,L)=1,BDismax(a,b,L)≠1的活动对(a,b)) 3.利用定义12计算BDismin(a,b,S) 4.if BDismin(a,b,S)>1 5.then根据定理2可知活动a和活动b之间存在skip类型的隐变迁。 6.for(所有and-split变迁和and-join变迁) 设t1为and-split变迁,t2为and-join变迁 7.if(λ(t1)≠τ∧λ(t2)≠τ∧BDismin(t1,t2,L)≠BDismax(t1,t2,L)) 8.then计算BDismin(t1,t2,S) 9.if BDismin(t1,t2,L) 10.then根据定理3可知在t1和t2之间的并发分支上存在skip类型的隐变迁。 11.else if(λ(t1)=τ,λ(t2)=τ) 12.then设∀c∈·(t1)T,∀d∈(t2)T·,a,b∈(t1)·T, 13.if(BDismin(c,d,L)≠BDismax(c,d,L)) 14.then计算BDis‖min(t1,t2,S) 15.if∃σ∈L,a∈σ∨b∈σ∧BDismin(c,d,σ) 16.then根据定理3可知在t1和t2之间的并发分支上存在skip类型的隐变迁。 17.得到带多类型隐变迁的Petri网模型M1。 对于第3章中的初始Petri网模型M0,由算法2步骤5可知,在活动对(a,d),(a,e),(b,d),(b,e)之间存在隐变迁t1。同理可以发现skip类型的隐变迁t3和t4,最终得到带多类型隐变迁的优化Petri网模型M1,如图11所示。 本章通过实验比较了本文方法与现有的隐变迁挖掘方法,验证了该方法的有效性。通过多组事件日志比较了几个挖掘算法在隐变迁发现个数和过程模型质量方面的差异。实验实施环境为Intel i7-6500处理器和8 GB的RAM(2.50 GHz)。采用文献[13]中提出的“token game”的方法来计算适合度,采用文献[14]和文献[15]中提出的方法计算模型的精确度和量化被发现模型和原模型间的一致性度。 通过模拟已知过程模型的运行得到事件日志,其中产生日志的每个原模型中都存在数量不等的各种类型隐变迁的组合。其活动的最大数量不超过20个,在不考虑频度的前提下,一个事件日志中的迹的总条数不超过30条。图12给出了IM算法、α#算法和本文方法在隐变迁识别个数、模型适合性、模型精确和模型的一致性4个方面的比较结果。 其中:图12a表明本文的方法能识别源模型中的多类型隐变迁,在识别隐变迁的个数上位于IM算法和α#算法之间,不会产生过多的冗余变迁。图12b和12c表示本文方法相比IM算法和α#算法在不降低模型精确度的基础上,进一步提高了模型的适合度,图12d表示本文方法相比IM算法和α#算法挖掘得到模型的行为与原模型的行为一致性更高。总之,实验结果表明,本文提出的基于行为距离的带隐变迁的过程挖掘方法能发现多类型的隐变迁,在不降低模型精确度的前提下,提高了模型的适合度。 本文提出了基于行为距离的带隐变迁过程模型挖掘新方法,首先,为了更精确地捕获活动间的依赖关系,计算了活动基于日志的最小和最大行为距离,通过活动间的弱序关系和行为距离详细分析了活动基于事件日志的基本行为关系。然后,利用行为关系和行为距离相结合的技术构建了带网关类型和循环类型隐变迁的初始过程模型。在此基础上,通过分析活动对基于日志、基于模型或基于并发结构的行为距离间的关系来识别skip类型隐变迁。最后,通过实验验证了该方法的有效性和优越性。未来工作主要有两个方面:①考虑如何改进该方法将其拓展到非自由选择结构;②当日志的行为关系不完备时,如何正确的发现活动间的可能行为关系和隐变迁的挖掘方法。3 构建带and网关类型和循环类型沉默变迁的初始过程模型


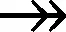
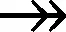
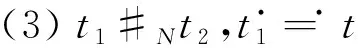


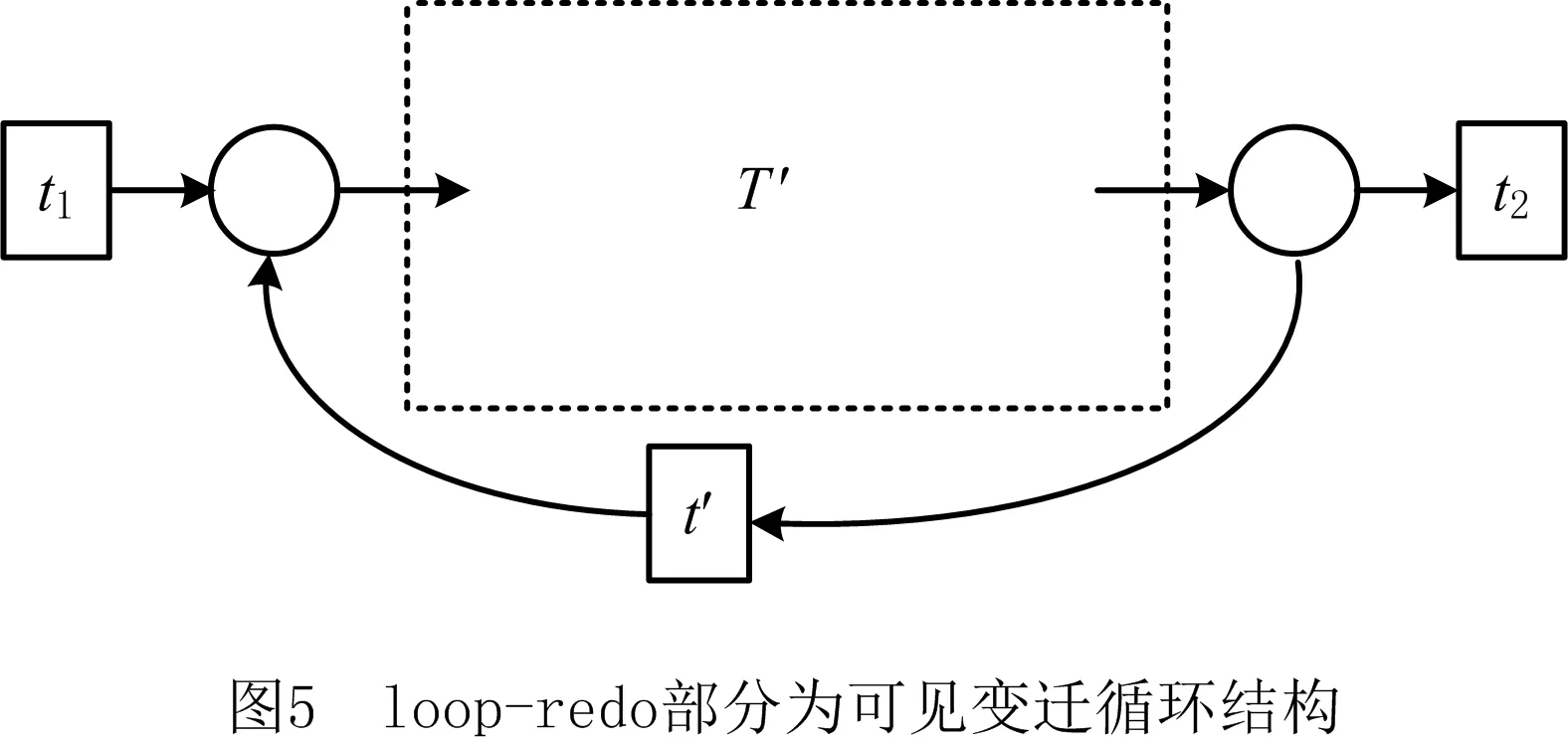
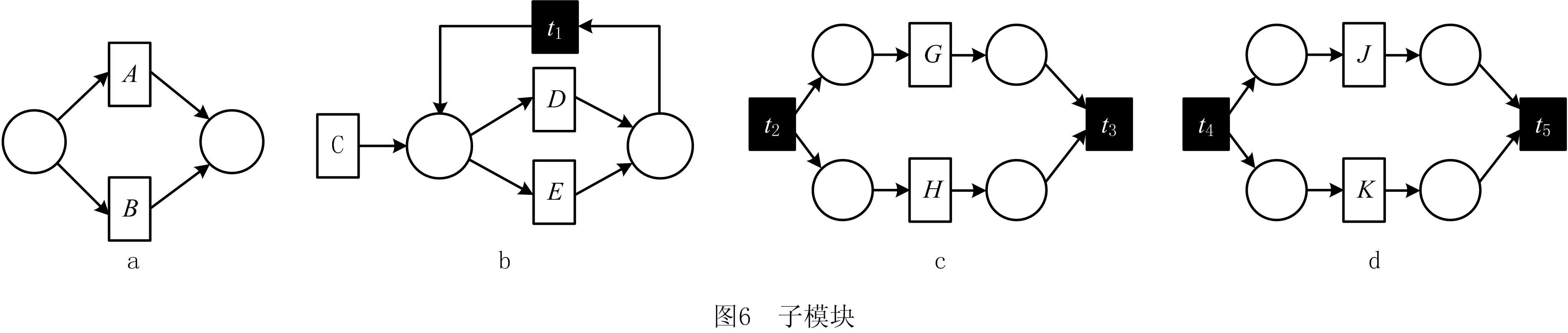
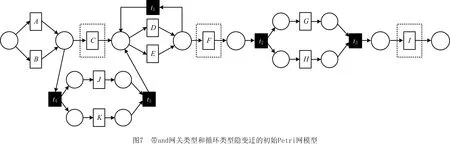
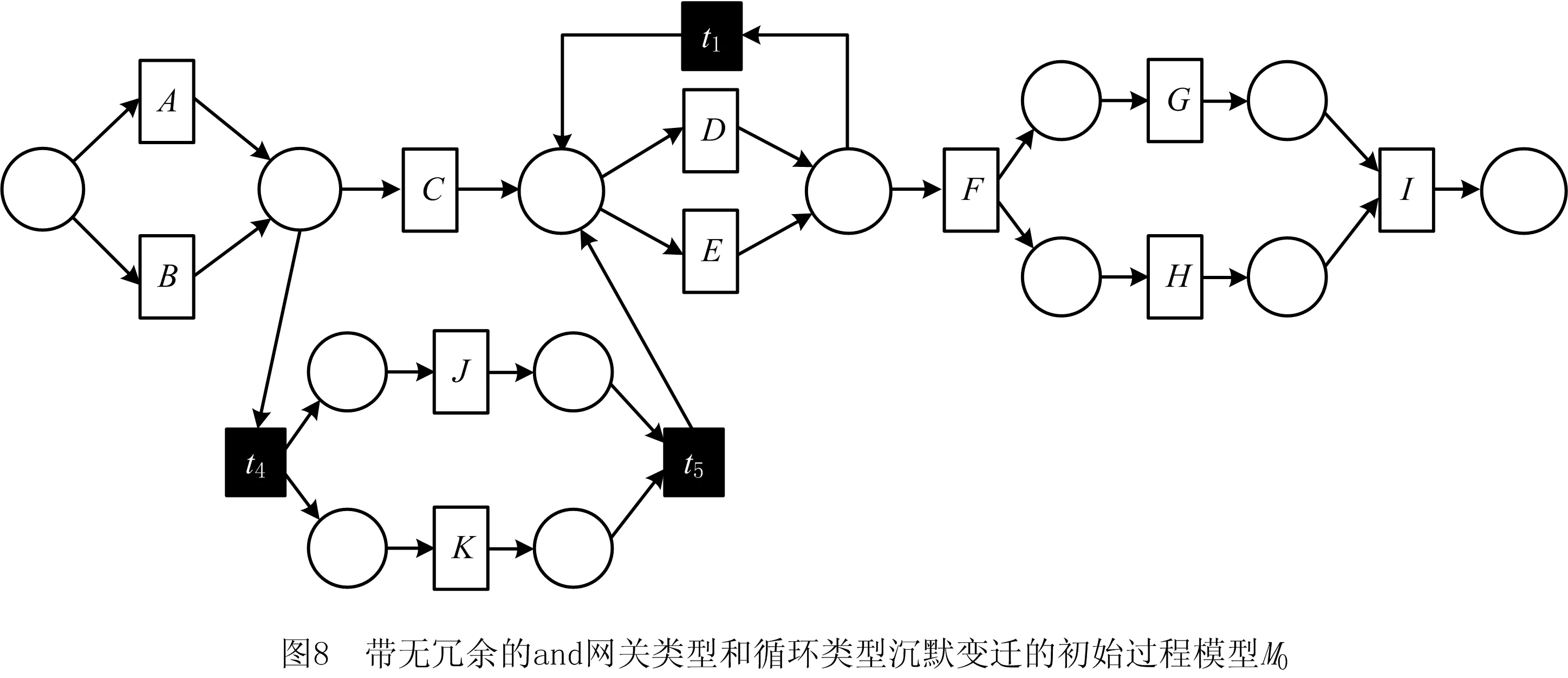
4 基于模型和日志的行为距离挖掘skip类型隐变迁
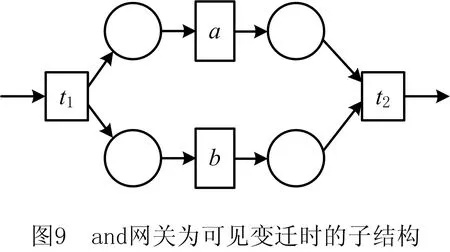
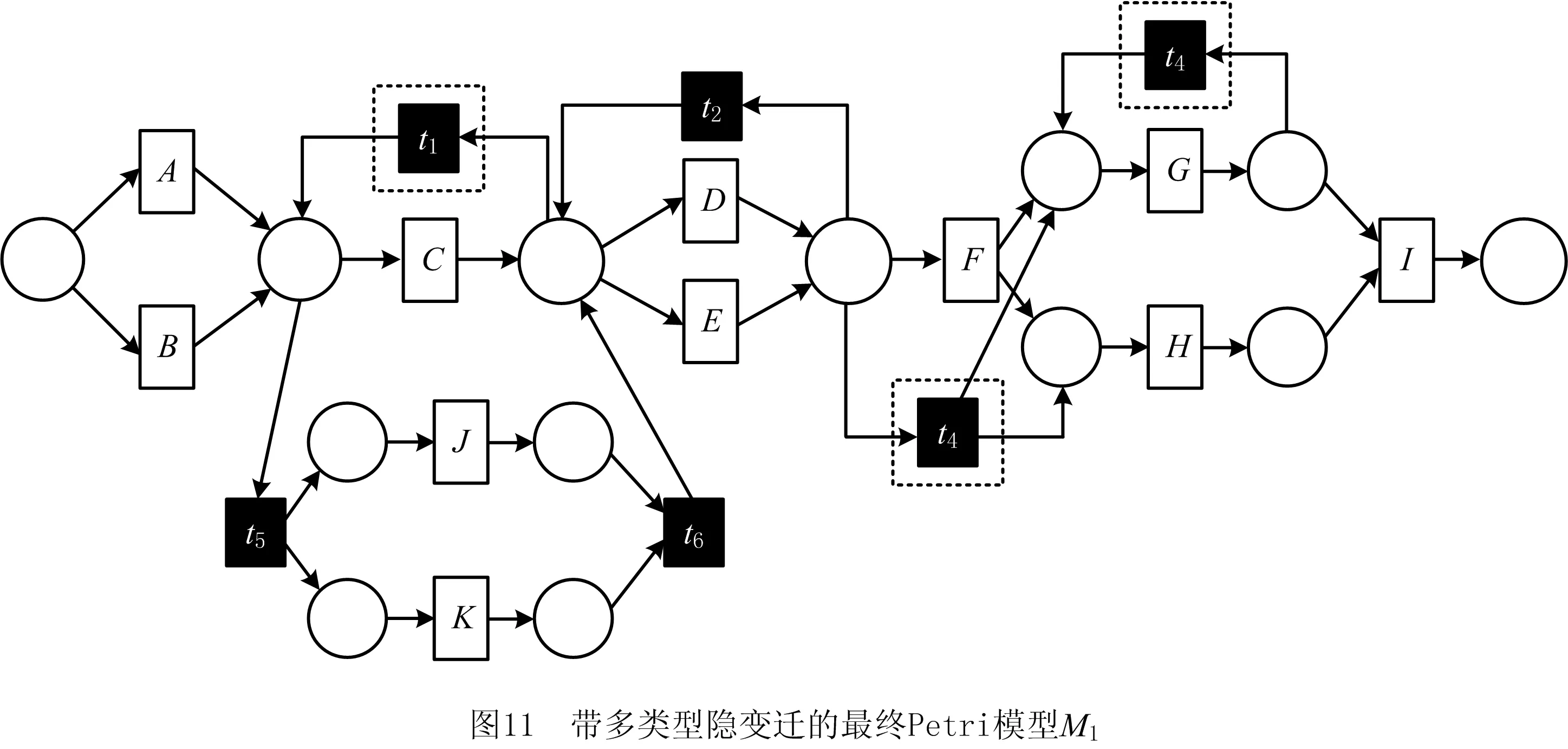
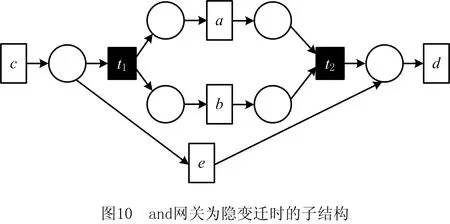
5 实验分析

6 结束语
