基于过程模型约束的轨迹乱序事件修复方法

2021-10-11闻立杰邓雅方王建民

计算机集成制造系统 2021年9期

王琦，闻立杰，邓雅方，钱忱，王建民

(清华大学软件学院，北京 100084)

0 引言

随着企业信息化的推进，海量的日志数据源源不断地从企业信息系统中产生，促进了信息挖掘领域的发展。与此同时，日志的完备性一直是备受关注的问题，由于系统原因或者人为原因，常常会导致系统日志中的时间信息错误，使得日志数据无法正确表达业务活动之间的次序关系，增加了信息挖掘的难度。此类可以表达活动之间相对次序关系的日志被称为轨迹日志。针对轨迹日志的乱序问题，业内提出了许多修复的手段用来提升日志质量。

目前，基于模型约束的轨迹对齐是主要的修复方式，LEONI等[1]最早提出利用流程模型和日志轨迹对齐修复日志的方法，可以对日志中存在的多种问题进行修复,然而此类修复方法的时间效率表现较差；为了提升对齐算法性能，业界学者提出一种分治的策略，将大规模流程模型分解为易于分析的子流程模型集，大大提升了算法性能[2]；在分治的基础上，SONG等[3]利用剪枝规则，进一步提升了对齐修复方法的性能。

此外，基于启发式的轨迹修复方式Effa[4]，虽然获得了良好的性能表现，但是修复准确率有待提高。针对轨迹修复问题，ROGGE-SOLTI[5]等提出结合随机Petri网、对齐和贝叶斯网络来实现轨迹修复的方法。有学者提出了修复轨迹缺失事件的分支定界修复方法[6]，还有基于时间约束网的乱序轨迹修复方法等[7]。

针对上述问题，本文围绕轨迹乱序问题展开研究，提出乱序轨迹的高效修复方法，主要贡献如下：

(1)首先对轨迹乱序问题的最优修复进行了形式化定义，并提出了基于移动距离的修复代价函数。

(2)提出一种基于A*算法的乱序轨迹修复方法，通过将轨迹与流程模型进行对齐，来寻找乱序轨迹的最优修复。

(3)提出一种基于精炼流程结构树的乱序轨迹修复方法，通过模型分解技术，将原始模型分解为多种不同类型的子结构，然后通过事件重放算法对模型子结构进行修复，修复效率获得了明显提升。

(4)设计了实验对本文提出的两种修复方法进行测试分析，并与业内主流修复方法进行了对比实验。

1 预备知识和问题定义

1.1 预备知识

本文以乱序轨迹日志的修复为主要目标，本节将对研究内容所涉及的预备知识进行说明，主要包含建模语言的选择和流程模型的定义。

定义1轨迹。轨迹是多个活动的非空有序集合，实际发生的活动在轨迹中称为事件。

本文使用Petri网作为主要建模语言[8]，Petri网是由Carl Adam Petri设计发明，用来描述非同步的因果和非因果行为的表达。

定义2Petri网。一个Petri网N是一个三元组(P,T,F)，其中：P为有限的库所集合；T为有限的变迁集合，且P∪T≠∅∧P∩T=∅；F⊆(P×T)∪(T×P)，为有向边集合(即流关系)；对于任意节点x∈P∪T,·x={y|(y,x)∈F}，x·={y|(x,y)∈F}。

定义3流程模型。一个Petri网N=(P,T,F)是一个工作流网，当且仅当下列条件同时成立：①有且仅有一个输入库所i∈P(源库所)满足·i=∅；②有且仅有一个输出库所o∈P(汇库所)满足O·=∅；③任意节点x∈P∪T都在源库所到汇库所的某一条路径上。

定义4前序集合和后序集合。对于一个流程模型N=(P,T,F)，σ为对应的触发轨迹，任意事件e∈σ，*e表示事件e的前序事件集合，包含从轨迹的开始事件到当前事件e之间的所有事件。e*表示事件e的后序事件集合，包含从当前事件e到轨迹最后一个事件之间所有的事件。

1.2 问题定义

轨迹的乱序问题是指轨迹中事件的相对顺序存在错位。在乱序轨迹修复过程中充满了不确定性和多样性，同一乱序轨迹存在多种修复方式和不同修复结果，为了量化轨迹修复过程中事件移动的代价，并提供一种对修复结果评价地方式，提出了基于位置的移动距离代价函数。

定义5位置映射函数。给定一个事件日志轨迹σ，σ可以被等价地转换为位置映射函数πσ，其中πσ关联事件和位置信息，即∀e∈σ，πσ(e)=k，其中k为事件e的位置信息。

轨迹中事件的位置分为两种类型：①在未修复的原始轨迹中，一个事件的位置信息对应该事件在轨迹中的索引下标，从1开始逐一递增至轨迹长度，即1～|σ|；②间隙位置，间隙位置k(x)就表示位于初始位置k和k+1之间的第x个事件。对于一条待修复轨迹σ=，如图1所示为轨迹事件的初始位置信息，若将T2前移到T3之前，则事件T2的新位置为1(1)，表示介于位置1和2区间内的第一个事件。

事件的移动将伴随着位置的修改，将轨迹修复前后事件位置的变化定义为轨迹的修复代价。

定义6移动距离(MD)。原始待修复轨迹σ的位置映射函数为πσ，修复轨迹σ′对应位置映射函数为πσ′，将修复的代价定义如下所示:

MD(σ,σ′)=∑t∈σ|πσ(t)-πσ′(t)|。

本文使用移动距离衡量原始待修复与修复轨迹之间的差异大小，最优修复轨迹定义如下。

定义7最优修复。对于过程模型N=(P,T,F) 的一个日志轨迹σ，最小修复轨迹σ′需要满足如下条件：

(1)σ′|=N；

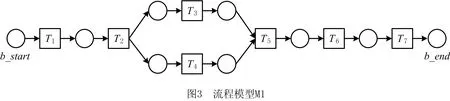
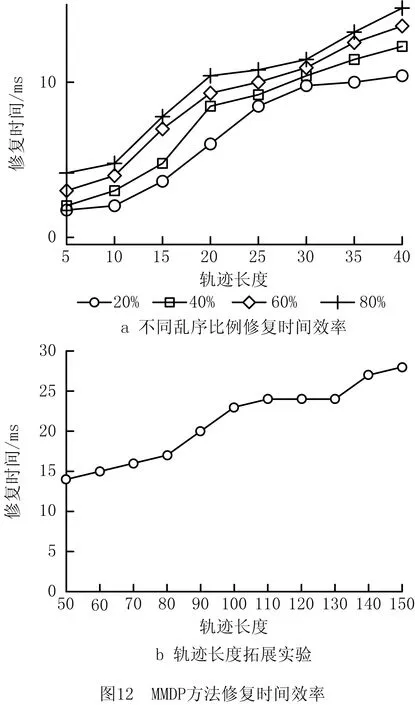
(2)MD(σ,σ′)最小，当且仅当不存在修复方案σ″，使得MD(σ,σ″)

2 基于A* 的乱序轨迹修复方法

A*(A Star)算法最早由Hart等[9]提出，被认为是最著名的人工智能算法之一。过程挖掘领域常用A*算法在搜索空间内寻找最优解，A*算法是基于启发式的路径搜索算法，可以在静态网络中搜寻最小路径。目前该算法已经用于解决各个领域的问题，例如DNA序列的比对、智能路径规划以及物联网智能流量等[10-13]。

本文提出的基于A*算法的乱序轨迹修复方法(Minimum Moving Distance repair using A*,MMDA)由轨迹事件优先级分析和解的搜索空间遍历两部分组成，修复方法的流程描述如图2所示。

2.1 事件优先级分析

MMDA方法在修复过程中，通过调整轨迹事件的相对位置，获得无错位事件的轨迹。为识别和修复轨迹中的错位事件，需要分析模型中的约束信息，判断轨迹中两个事件之间的相对顺序是否发生错位。

流程模型中的约束关系决定了变迁节点之间的触发顺序，本文将变迁节点的触发先后次序关系定义为变迁优先级，定义如下：

定义8变迁优先级。给定一个无环流程模型N=(P,T,F)，模型的开始节点为b_start，结束节点为b_end，∀t1,t2∈T，m(t1)和m(t2)分别表示变迁t1和t2在流程模型N中的变迁优先级，F(t1,t2) 表示从t1开始到节点t2之间所有路径包含的变迁集合，变迁优先级遵循如下规则:

(1)m(t1)>m(t2)，如果满足t2∈F(t1, b_end)，或者t1∈F(b_start,t2)；

(2)m(t1)

如图4所示，如果流程模型内部包含循环结构，将存在若干条从后向前的反向边，在分析变迁优先级时，需要将循环结构进行展开操作，总是将L2中变迁优先级小于L1中的变迁优先级，L3结构中变迁优先级小于L2中的变迁优先级，即∀t0∈L0，∀t1∈L1，∀t2∈L2，∀t3∈L3，满足m(t0)>m(t1)>m(t2)>m(t3)。

轨迹中每个事件都是由对应的模型变迁节点触发生成，通过分析模型变迁节点的触发次序，进而可以推断轨迹中事件的生成顺序，首先给出事件优先级的定义。

定义9事件优先级。给定一个日志轨迹σ，∀e∈σ，d(e)表示事件e的事件优先级。∀e1,e2∈σ，事件优先级表示事件的触发生成次序先后关系：

(1)若d(e1)>d(e2)，表示事件e1在模型中的触发生成次序早于事件e2；

(2)若d(e1)

(3)若d(e1)=d(e2)，表示在模型中对事件e1和e2之间的触发次序无要求。

通过将轨迹事件与模型变迁进行一一映射，获得事件优先级信息。对于仅包含串行、互斥分支和并行结构的流程模型，使用同名映射方式，t=φ(e)表示与事件e同标签名的变迁节点t。

规则1普通事件优先级比较规则给定一个无环流程模型N=(P,T,F)和对应的日志轨迹σ，∀e1,e2∈σ，则事件优先级的比较遵循以下规则:

(1)若m(φ(e1))>m(φ(e2))，则事件优先级满足d(e1)>d(e2)；

(2)若m(φ(e1))

如图3所示的流程模型，对于一个待修复轨迹σ=，按照模型和上述定义，可以推断出d(T1)>d(T2)，代表事件T1的生成次序应早于事件T2，但是在轨迹σ中，事件T2却出现在事件T1之前，因此可以判断事件T1和T2之间存在错位问题。

如果模型中包含循环结构，轨迹中会包含多个同标签的事件，需要按照循环次数进行切分，从而区分多个同标签事件。如图5所示包含循环结构的流程模型，给定一个待修复轨迹σ，按照事件在轨迹中的出现顺序，将循环事件切分为S1和S2两部分，属于循环触发S1中的事件优先级一定大于属于S2中的事件，即∀e1∈S1,e2∈S2，满足d(e1)>d(e2)。

给定一个日志轨迹σ，如果修复后的轨迹σ′，满足：∀0

2.2 搜索空间的生成与遍历

为了使用A*算法寻找最优修复，需要定义一个合适的搜索空间，搜索空间中的节点代表修复的过程，原轨迹作为初始节点出现在搜索空间中，空间中相连的两个修复节点代表修复过程的连续性，每一个部分修复轨迹经过一次修复，都可能生成多个新的轨迹，将轨迹的修复操作定义如下：

定义10错位事件修复函数。给定一个流程模型N=(P,T,F)，对于一条部分修复轨迹σ，∀e1∈σ，错位事件修复函数ad(e1,σ)表示以事件e1为基准，调整轨迹中的错位事件，生成新的轨迹，调整规则如下:

(1)∀e2∈*e1，且d(e2)

通过连续的调用错位事件修复函数，可以渐进性的对待修复轨迹进行修复；同时，以不同的事件作为参数调用修复函数，可以生成不同的新轨迹，对应不同的修复分支。如图3所示的流程模型，给定对应的一个待修复轨迹σ=，其生成的局部修复分支如图6所示。

如果修复后的新轨迹是一条完全修复轨迹，则暂存当前修复轨迹和对应的修复代价。因为修复的多样性，在生成修复分支的过程中，将获得多个不同的完全修复轨迹和对应的修复代价，根据最优修复的定义，选取修复代价最小的一条完全修复结果作为最优修复。

除此之外，待修复轨迹修复遍历的过程中，会出现许多等价的部分修复轨迹，如图6中所示，通过ad(T2,σ)和ad(T3,σ)修复后得到的新轨迹是等价的，即轨迹中对应事件的顺序完全一致，为了加速遍历算法，对于等价的轨迹，只保留修复代价(移动距离)较小的轨迹即可。

2.3 代价预估启发式

代价预估启发式是A*算法的重要组成部分，A*算法会维护一个优先级队列，在修复过程中，将所有部分修复轨迹加入到队列中，其中预估修复代价越小的部分修复轨迹，在队列中优先级越高，越容易被优先修复。理想情况下，通过优先级队列和代价预估启发式，A*算法能够优先获得修复代价最小的修复结果，并且将后续预估代价较大的修复分支进行修剪。

对于一个待修复轨迹σ，假设轨迹的修复预估代价为LHσ，实际修复代价为MDσ，为了获得预估修复代价的计算方式，首先可以对流程模型中的两个相邻变迁节点进行分析。给定一个流程模型N=(P,T,F)，模型N的任意两个相邻变迁节点x和y，满足y∈(x·)·，将存在以下几种情况：

情况1∃i

情况2∃i

(1)将σ(i)移动到σ(j)之后，如图7b所示，y′为y的新位置，事件修复的移动代价为Costij=j-i；

(2)将σ(j)移动到σ(i)之前，如图7c所示，x′为x的新位置，事件修复的移动代价为Costij=j-i；

(3)σ(i)和σ(j)同时移动位置进行修复，如图7d所示，事件x和y同时向中间的某个事件位置k进行移动，事件修复的移动代价为Costij=(j-k) + (k-i)=j-i；如图7e所示，事件同时向y左侧的某个事件位置k进行移动，则事件修复的移动代价Costij≥j-i；同理如7f所示，也满足Costij≥j-i；

按照上述的分类讨论得知，不管如何修正事件错位问题，都有Costij≥j-i。

情况3不存在i

由上述讨论可知，对于模型中的两个相邻变迁x和y，只要其对应的事件相对顺序错误，其修复代价一定大于其位置差值的绝对值。同时，为了防止最终预估的代价超过实际修复代价，同一个模型变迁及其对应的轨迹事件在代价预估的过程中，应该仅被使用一次，因此提出后继二元集的定义。

定义11后继二元集。给定一个流程模型N=(P,T,F)，后继二元集(Subsequent Binary Set，SBS)是一个二元组的集合，其中∀(x,y)∈SBS满足如下条件:

(1)x∈T，y∈T，并且y∈(x·)·;

(2)不存在其他的一个后继二元组(m,n)，使得x或y包含在(m,n)中。

对于部分修复轨迹σ，将其完全被修复所需要的代价称为剩余修复代价，基于上述讨论和后继二元集，下面给出剩余修复代价的预估方式。

定义12剩余修复代价。设函数k(a,b)表示修复事件a和b所需要的预估代价，在此给出剩余修复代价的预估函数

FCσ=∑∀(a,b)∈SBSk(a,b)=

FCσ是对修复代价的一种预估值，始终满足0≤Fcσ≤MDσ,即预估剩余修复代价始终小于实际修复代价。对于修复过程中的一条部分修复的轨迹σ′，将其全部的修复代价预估定义如下:

LH(σ,σ′)=MD(σ,σ′)+FCσ′。

其中：MD(σ,σ′)是已有的修复代价，FCσ′是轨迹完全被修复所需要的剩余修复代价，两部分修复代价共同构成了轨迹σ′的预估修复代价。在遍历解空间的过程中，已知一个已经产生的修复方案的代价为MDσ′，可以将该方案的修复代价设置为剪枝阈值。对于遍历过程中的任意一个修复节点σ″，计算σ″对应预估修复代价LH(σ,σ″)，将预估代价与剪枝阈值进行比较：

(1)LH(σ,σ″)≥MDσ′，则该节点最终修复方案的修复代价一定大于MDσ′，可以安全地修剪掉当前分支；

(2)LH(σ,σ″)

通过修复代价预估对搜索空间内的无用修复分支进行修复，从而加速修复算法的时间效率表现，基于A*算法的乱序轨迹修复方法的实现如算法1所示。算法第1行首先声明一个优先级队列Q，内部存放轨迹和位置信息的二元组；第3行表示每次从队列Q中选择一个预估代价最小的部分修复轨迹进行修复；第7行表示调用错位事件修复函数生成新轨迹；第8行表示修复后的轨迹符合模型约束，始终保留修复代价最小的修复结果；第11行表示新轨迹中仍然存在乱序问题，加入到队列Q中；最后返回最优修复结果。

算法1基于A*算法的乱序轨迹修复方法。

输入：工流程模型Ns、待修复轨迹σ及其位置映射函数πσ；

输出：最小修复方案σmin和位置映射函数πmin。

1 Q：={(σ, πσ)}，(σmin,πmin)：=NULL

2 while Q≠∅ do

3 (σ,πσ′)：=argmin(σ′,πσ′)∈QLH(σ,σ′)

4 Q：=Q{(σ,πσ′)}

5 ifLH(σ,σ′)

6 foreach e∈ECSσ′do

7 (σ″,πσ″)：=ad(e,σ)

8 if (σ″,πσ″)|=Nsthen

9 (σmin,πmin)：=Min((σ″,πσ″),(σmin,πmin))

10else

11Q：=Q∪{(σ″,πσ″)}

12 returnσmin,πmin

3 基于精炼流程结构树的乱序轨迹修复方法

基于A*的乱序轨迹修复方法，需要遍历整个解的搜索空间，寻找修复代价最小的修复结果作为最优修复。因此，为了加速修复方法的修复性能，提出一种基于精炼流程结构树的修复方法(Minimum Moving Distance repair using refined Process structure tree，MMDP)。精炼流程结构树 (Refined Process Structure Tree，RPST)最早由Polyvyanyy等[13]提出,是一种流程模型的层次化结构表示，可以将流程模型转换为由多个单入单出子结构表示的树状结构，每个子结构称为组件。MMDP方法流程框架描述如图8所示。

3.1 模型分解

RPST的叶子节点代表了流程模型中的边，在进行轨迹修复前，需要将边转换为变迁节点，转换规则如下：

规则2变迁节点转换规则。

每一个RPST中的叶子节点，都对应流程模型中的一条边，每条边都关联一个变迁节点，若变迁节点只归属于一个组件，则直接转换；若变迁节点同时属于多个组件，则重复归属于多个组件中。

3.2 自顶向下的轨迹修复

从上到下依次遍历RPST中的每一个组件，对于每个组件中包含的模型变迁节点，需要从轨迹中抽取对应的事件，分离为单独的轨迹片段。给定一个流程定义N，待修复轨迹σ，对应位置映射函数π，对于遍历过程中的一个组件S，分以下几种情况讨论：

情况1S是B组件，B组件同时可以表示互斥分支结构、并发结构和循环结构，细分为以下3种情况处理:

(1)S是互斥分支B组件，则S一定包含多个子组件，只需进行子组件的修复即可;

(2)S是并发B组件，首先需要将以S为根结点的所有子组件标记为MMDA修复组件，然后进行子组件的遍历;

(3)S是循环B组件，使用MMDA方法直接修复S对应的轨迹片段σ′，无需继续向下遍历。

(1)若S除包含组件外，还包含其他组件，需继续向下进行子组件的遍历修复;

(2)若S仅包含组件，且没有被标记为MMDA修复组件，则可利用轨迹重放算法修复，如算法2所示；

情况 3S是组件，无需修复，组件内部仅包含一个变迁节点，对应轨迹片段不存在错位问题。

情况 4S是R组件，非结构化部分，使用MMDA修复对应轨迹片段。

对于不同的组件，首先抽取对应的轨迹片段，然后分类别进行修复。轨迹重放算法如算法2所示。第1行定义最终返回的最小修复轨迹，集合history为已经触发过的事件集合；第2行表示遍历模型变迁，进行对比重放；第3～第4行表示跳过已重放事件；第5～第8行表示当前事件σ′(i)可以被重放，然后添加到结果当中；第9～第11行表示当前事件σ′(i)无法被重放，需要从轨迹中寻找一个可以被重放的事件t进行重放;第12行更新当前可达模型变迁；最后返回重放结果。

输入：RPST 组件的开始节点 Ms、结束节点 Me和对应轨迹片段σ′；

输出：最小修复轨迹片段σmin。

1 σmin：=<>, M：=Ms, history：=∅, i：=0

2 while M≠Me do

3 if σ′∈history then

4 i：=i+1

5 if M[σ′(i)>M′ then

6 σmin：=σmin·σ′(i)

7 history:=history∪{σ′(i)}

8 i：=i+1

9 else∃t∈σ′,M[t>M′then

10 σmin：=σmin·t

11 history：=history∪{t}

12 M：=M′

13 returnσmin

3.3 自底向上的轨迹合并

修复后的轨迹片段需要进行合并整合，获得最终的修复轨迹，在合并过程中，不仅需要保持组件内部事件的有序，还要保证组件之间的有序。对于同属一个父节点的两个组件P1和P2，对应修复后的轨迹片段为σP1和σP2，提出以下两种合并方式:

(1)交叉合并。轨迹片段σP1和σP2，按照事件位置从小到大进行排列合并，相同位置的事件按照原待修复轨迹中的出现次序排列，并对重复的开始节点和结束节点进行判断去重;

(2)追加合并。轨迹片段σP1或σP2，需借助2.1节中的变迁优先级进行合并，子结构P1的开始节点MP1和子结构P2的开始节点MP2，若m(MP1)>m(MP2)，则直接将轨迹σP2追加到轨迹σP1之后，否则将轨迹σP1追加到轨迹σP2之后。最后，判断合并组件中，前一个组件的结束节点和后一个组件的开始节点是否重复，进行节点去重。

(2)B组件包含的子组件，使用交叉合并方式合并子组件对应的修复轨迹片段。

4 实验评估

实验部分除了本文提出的两种修复方法之外，还将与Effa[4]和对齐Alignment[1]方法进行对比。实验数据主要分为企业流程模型数据集和人工实验数据集两大类。数据集详细信息如表1所示。

表1 实验使用的3种数据集统计信息

基于流程模型，使用日志生成器BeehiveZ生成正确的模型日志轨迹，根据实验要求，使用ProM的DisorderLog插件对轨迹数据进行事件乱序处理。

4.1 基于企业数据集实验

4.1.1 修复效率实验

如图9所示为修复时间效率对比结果，本实验将超过10 000 ms的修复过程视为超时修复，不再进行最终时间的统计。分析实验结果可得：Alignment方法修复效率最慢，MMDA修复时间效率明显优于Alignment；MMDP方法的修复效率要优于MMDA，说明基于RPST的加速方式起到了明显的效果；此外，基于启发式的Effa修复方法是最快的。

4.1.2 修复精度实验

如图10a所示为因果网数据集最小修复精度对比实验结果，因果网是只包含顺序结构和并发结构的流程模型，其中MMDA,MMDP和Aligament修复精度较高；虽然Effa方法修复速度较快，但是修复精度较低，启发式无法确保修复结果为最优修复。

如图10b所示为包含循环结构的数据集绝对修复精度实验结果，其中MMDA和MMDP方法可以较好地对包含循环结构的乱序轨迹进行修复；Effa方法修复精度最低，这是由于其循环切分规则导致的。在修复过程中，Effa方法会首先选取轨迹中的某个事件作为切分点，然后直接将原始轨迹切分为多个片段，在每个片段内对轨迹进行修复，修复结果的好坏，很大程度上取决于循环切分点的选择。

4.2 人工数据集实验

4.2.1 MMDA方法

如图11a所示为 MMDA方法的时间效率实验结果图，设置了4个轨迹事件乱序比例:20%、40%、60% 和 80%。由实验结果可知，修复方法的性能表现不仅受到轨迹长度的影响，还受到轨迹内事件乱序程度影响。

为了验证等价轨迹检测剪枝规则对修复方法性能的加速作用，进行了如图11b的实验。图中纵坐标轴为修复算法遍历的修复节点总数，由图可知，采用剪枝的修复方法遍历节点数始终低于无剪枝的修复方法，这也证明剪枝规则对修复方法起到了有效的加速作用。

4.2.2 MMDP方法

图12a 所示为 MMDP方法时间效率实验结果图，分别选取了4个不同的轨迹乱序比例:20%、40%、60% 和 80%。相较于图11a，MMDP性能表现更好，因为在遍历的过程中，MMDP避免了大部分分支遍历和分支回滚。除此之外，通过对比图中不同的乱序比例修复曲线，可得 MMDP方法受轨迹乱序比例影响较小。

图12b所示为拓展实验，根据文献[15]的调研结果显示，一般企业级别的流程，上限活动数目为60个，实验中将流程模型变迁节点数量上限拓展为150个，修复方法仍然可在30 ms内完成修复，相较于MMDA方法，性能提升效果明显。