不完备事件日志下的业务系统变化检测及模型修复方法
2021-10-11郑雪文王吴松
方 欢,郑雪文,王吴松
(安徽理工大学 数学与大数据学院,安徽 淮南 232001)
0 引言
随着大数据技术的蓬勃发展,业务流程管理及优化在企业的日常管理中发挥着越来越重要的作用,然而业务流程可能随着时间的推移不断地发生演变,以至于日志行为和模型行为之间存在差异,实际系统日志无法在模型中回放[1]。变化原因包括法规、政策、用户需求和软件维护等因素[2]。这些因素在影响业务流程发生变化的同时,也可能改变系统的业务能力和行为,因此高效、正确地检测业务流程变化,并及时对业务系统模型进行修复具有较高的研究价值。
近年来涌现的基于完备日志的模型修复研究得到了诸多科研工作者的青睐。如文献[3]研究了现有的一致性检查器,将给定的过程模型与日志中的迹对齐。基于此,将日志分解为不适合子迹的子日志。对于每个子日志,派生一个子过程,然后将其添加到原始模型适当的位置。文献[4]提出将预定义的成本分配给修复动作(插入或跳过活动)的方法,使得对齐的计算量大大减少,同时得到最佳修复。文献[5]提出一种用于过程模型修复的模块化方法,可以使用不同的算法作为构建块来实例化该方法。其主要思想是使用模型分解,找到不符合要求的片段,并用符合要求的片段替换,而不是完全重新发现。文献[6]提出的方法可以在选择结构中添加新的活动,它引入了一种新的偏差类型:选择分支偏差,同时在流程模型和事件日志之间定义了扩展的对齐方式。若在选择结构中找到该偏差,则可以将该偏差作为分支添加到原始模型中。文献[7]提出一种新的基于Petri网的模型修复方法,该方法能使在原始模型中只能发生一次变迁,在修复后的模型中可以随时发生。
以上研究方法大都基于Petri网的模型修复,然而,近两年出现了一些基于逻辑Petri网(Labled Petri Nets,LPN)[8-13]的模型修复方法。例如,文献[8]提出通过LPN的现有方法来分别修复包含顺序结构和并发结构的过程模型。其主要思想是通过识别新活动找出事件日志中的迹与流程模型之间的偏差。然后可以分别构造新活动的前继和后继集,以及每组活动间的关系,最后构造逻辑关系函数。文献[9]提出的模型修复方法首先定义了新活动和原始活动之间的两种新关系,分别称为逻辑并发关系和因果关系。然后,构造一个梯形矩阵,并获得原始过程模型和事件日志之间的偏差。接下来,使用偏差矩阵记录这些差异以修复模型。文献[10]中的并发变迁对和选择变迁对是基于过程树构造的。通过遍历最佳对齐,确定并发块头和尾之间的变迁,偏差用于判断过程模型和事件日志中的活动是否具有并发变迁对或选择变迁对,然后通过LPN修复该模型。文献[11]提出了对于包含具有并发结构的一种模型修复方法。首先找到偏差的位置;然后,通过LPN添加从库所到变迁或从变迁到库所的有向弧;最后,通过添加带有逻辑函数的逻辑变迁来实现模型的修复。文献[12]首先定义一个新的事件日志类型:选择偏差子日志,然后,根据token的原理找到偏差位置重放。接下来,在选择分支之间添加桥以修复模型。文献[13]可以检查模型是否与事件日志匹配。根据不同的结构和一致性检查的结果获得偏差位置。在不添加隐变迁和重复变迁的情况下,通过添加弧和逻辑变迁来修复模型,并保留原始结构。
以上大都是基于系统原始参考模型已知的情况,对模型的修复存在局限性问题。在实际应用场景中,系统原始参考模型也可能未知,或者实际模型与原始模型存在部分差异的情况,且得到的系统日志是不完备的。完备日志是指日志包含所有业务活动以及活动间所有可能的行为关系,而不满足完备日志条件的日志称之为不完备日志。因此,有必要在系统参考模型未知和基于不完备事件日志的情况下[14-16]对业务流程的变化进行检测和模型修复。
本文的主要贡献包括:①在系统参考模型未知的情况下,依据当前实际系统不完备日志,得到日志迹中每个活动的直接前继和后继;②基于原始不完备事件日志发现的模型与系统实际日志不同的行为轮廓关系集,提出了一种日志偏差域的识别方法;③通过日志迹中每个活动的直接前继和后继以及偏差域,提出一种实现模型修复的方法。
1 研究动机
随着时间的演进,业务系统可能会引入一些变化操作,如活动的插入和删除等,这些变化操作势必会引起业务系统的行为发生变化[17],除此之外,现实生活中存在许多不完备的事件日志业务系统。由于要实现业务系统的变化检测及修复,需要了解系统的历史日志信息和当前实际系统日志信息。为了简化描述,记历史日志为Lhis,当前系统日志为Lact。
下面以一个简单的例子,从不完备日志的角度说明当前实际系统日志与系统模型不一致性的问题。利用具体的事件日志进行分析,选取一组日志,日志中的相关迹信息有:事件日志Lhis={
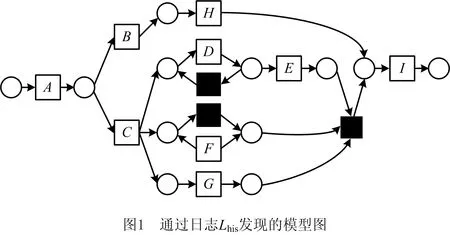
将日志Lact在图1的模型中回放可知,除了日志中的迹σ1与模型是一致的,其余的迹σ2到迹σ7都不能在模型中回放。可以看出,基于不完备事件日志的情况下,当前实际系统日志与业务系统模型之间也存在差异。因此,在不完备事件日志下对业务流程的变化检测和模型修复问题的研究十分必要。
2 基本定义
定义1[18]迹,事件日志。设A为所有活动的集合。若σ∈A*,则记迹为σ。如果L∈B(A*)且L是迹σ上的多集,则记L为事件日志,S(σ)表示σ中所有活动的集合。
例如,A={a,b,c,d}是一个活动集,σ=
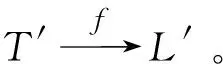
定义4[2]变化操作。L为一个事件日志,事件迹σ∈L,日志中的活动集合记为S,Delete和Insert分别指日志中活动的删除变化操作和插入变化操作。其中,Delete和Insert具体操作如下:∀ai∈S,σi∈L(i=1,2,…,n),
(1)Delete:Delete(σi,ai)删除操作是指把活动ai从迹σi中进行删除。
(2)Insert:Insert(si,ai)是指把活动ak插入到迹si中的任意位置;Insert(σi,ak,a1,a2)指在迹σi中,把活动ak插入到a2和a3之间(其中ak为新增活动)。
定义5[2,20-21]迹处理运算符。设L为A上的日志,num为日志中迹的个数,a∈A,∃σk=x1,x2,…,xn∧σk∈L∧a∈σk:
(1)τ(xi,σk)给出了σi中元素xi的活动名称。
(2)Pos(a,σk)={p,q,r,…,s},例如τ(xp,σk)=a,…,τ(xs,σk)=a。
(3)1-Pred(xi,σk)=τ(xi-1,σk),1-Succ(xi,σk)=τ(xi+1,σk),i是某一确切的数。
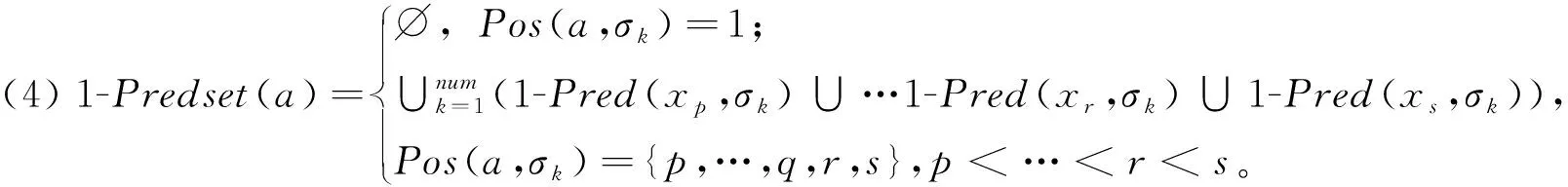
在定义5中,函数1-Pred和函数1-Succ分别提供了活动xi的直接前继和直接后继;函数1-Predset是日志中发生在活动标识符a之前的最近活动集合的并集;相反,1-Succset是指发生在活动标识符a之后的最近活动集合的并集。
3 基于不完备事件日志的偏差域识别
为了有效地分析不完备日志,需要提取日志的主要信息。由定义2可知,研究的不完备日志行为轮廓关系仅为所有的严格序和交叉序关系。已知原始事件日志Lhis和系统实际日志Lact,由算法1可以得到其行为轮廓关系,Ract表示一组基于系统实际日志的行为轮廓关系,Rhis表示一组基于原始日志的行为轮廓关系。算法2提出了基于行为轮廓关系矩阵的日志间比较算法。在算法2中,可以并行执行步骤5和步骤6以节省时间,从而得到Rhis和Ract。
算法1基于不完备日志的行为轮廓关系捕获算法。
输入:日志L;
输出:基于不完备日志的行为轮廓关系集。
1.R=∅,R→=∅,R||=∅
2.for each σ in L do
4.else if x≻y and y≻x then R||=R||∪(x,y) //(x,y)为交叉序关系
5.end for
6.R=R→∪R||
7.return R
定义6[18]日志偏差域。设A是日志中所有活动的集合Ract∪Rhis。对于∀ai,aj∈A,如果Ract与Rhis之间存在不同的关系表示为无匹配关系。日志偏差域是由无匹配关系构成的极小域,记为(ai,aj)。
由定义6,日志偏差域是原始日志与系统实际日志之间的不匹配域[22]。由算法3调用算法2 ,可直接得到日志偏差域D。D不仅记录不匹配的关系,还记录活动。因此,可以很容易地获得D中的活动信息。
算法2基于行为轮廓关系矩阵的原始日志与系统实际日志的比较算法。
输入:原始日志行为轮廓关系集Rhis,系统实际日志行为轮廓关系集Ract;
输出:Rhis和Ract之间的不同行为轮廓关系集。
1. Ahis表示Lhis中所有活动的集合,Aact表示Lact中所有活动的集合
2. D=∅,A=∅ //D表示Rhis和Ract之间不同的行为轮廓关系集
3. A=Ahis∪Aact,n=|A| //n表示活动集A中所有活动的个数,A中元素是顺序的
4. aact[n][n]={0},ahis[n][n]={0} //1(严格序关系);2(交叉序关系);0(其他)
5. for each element ∈Rhisdo ahis[i][j]=Rhis(ai,aj) //i,j=1,2,…,n
6. for each element ∈Ractdo aact[i][j]=Ract(ai,aj)
7. for (i=1;i≤n;i++) do
8. for (j=1;j≤n;j++) do
9. if aact[i][j]≠ahis[i][j] then
10.D=D∪{(aact[i][j],ahis[i][j])}
11.return D
算法3如下:
算法3基于不完备日志的偏差域识别算法。
输入:Ract,Rhis;
输出:基于不完备日志的偏差域(ai,aj)。
1. 调用算法2,得到D
2. for each element ∈D do return (ai,aj)
3. end for
4 基于不完备事件日志的模型修复
一些现有的一致性检查技术已经被用于修复过程模型,也有许多技术可以有效地发现日志行为差异[23]。本文研究了基于原始不完备事件日志挖掘的模型与系统实际日志的偏差域,提出一种模型修复的算法,使之重放系统实际日志。在进行具体修复过程前,利用算法4对基于不完备日志偏差域的变化活动进行捕获,从而获得个变化操作的变化活动集。
算法4基于不完备日志偏差域的变化活动的捕获算法。
输入:系统实际日志Lact,基于原始日志Lhis的Petri网N=(P,T,F);
输出:各变化活动集Adel,Ains及Amov。
1.G=Gd=Gk=Gm=∅,Adel=Ains=Amov=∅
2.调用算法1,得到基于日志的行为轮廓关系Ract和Rhis;调用算法2,得到D
3.for each element ∈D do //delete变化活动集Adel的捕获
4.if all aact[i][d]=aact[d][j]=0 and ahis[i][d]≠0 and ahis[d][j] ≠0 then
5.Gd=(0,ahis[i][d])-(0,ahis[d][j]), G=D-Gd
6.调用算法3,得到活动对(ai,ad),(ad,aj),Adel=Adel∪{ad},A=A-Adel
7.end for
8.for each element ∈G do//insert变化活动集Ains的捕获
9.if all ahis[i][k]=ahis[k][j]=0 and aact[i][k]≠0 and aact[k][j]≠0 then
10.Gk=(aact[i][k],ahis[i][k])-(aact[k][j],ahis[k][j]), G=G-Gk
11.调用算法3,得到活动对(ai,ak),(ak,aj),Ains=Ains∪{ak},A=A-Ains
12.end for
13.for each element ∈G do//move变化活动集Amov的捕获
14.if all ahis[i][m]≠aact[i][m] and ahis[m][j]≠aact[m][j] then
15.调用算法3,得到活动对(ai,am),(am,aj),Amov=Amov∪{am},A=A-Amov,Gm=G
16.end for
17.return Adel, Ains, Amov
大多数模型修复是基于对齐的方式。在对齐方法中,分为活动的跳过与移动。而在本文中,对于一个活动ad的删除是通过添加一个对应的排他关系的隐变迁τd来实现系统实际日志的回放,删除活动的修复方式具体如图2所示,主要区别在于删除活动的前继和后继的库所数。对比Rhis和Ract,可以发现一个活动的删除会导致系统实际日志中该活动与其他活动没有相对应的关系,即Ract中该活动对应的行与列均为空,具体修复步骤见算法5。
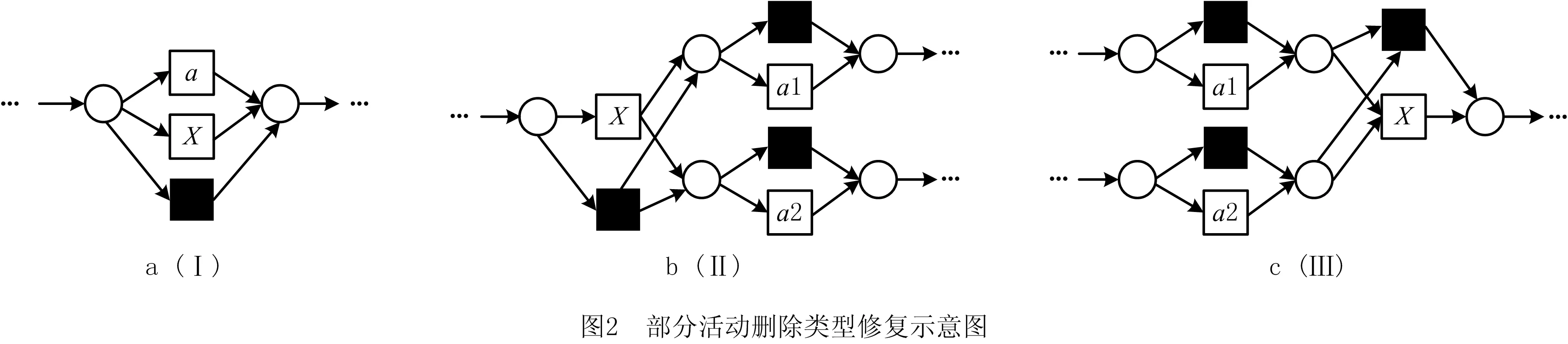
算法5基于不完备日志偏差域的模型Delete操作修复算法。
输入:delete日志偏差域Gd,delete变化活动集Adel,基于原始日志Lhis的Petri网N=(P,T,F);
输出:修复后的Petri网N1=(P1,T1,F1)。
1.for each ad∈Adeldo
2.Get(Pi,ad),(ad,Po)∈F,T1=T∪{τd},F1=F∪{(Pi,τd),(τd,Po)}
3.//其中Pi,Po为活动ad的前继库所集和后继库所集
4.//如果模型中已有隐变迁在该活动的跳过位置,则无需再添加跳过变迁
5.end for
6.return N1=(P1,T1,F1)
然而,在对由原始事件日志发现的模型中进行某一活动的删除处理时,可能发现模型中存在与该活动具有排他关系的隐变迁。由于日志迹行为关系中无排他关系,该种情况下不在另外插入排他关系的隐变迁。一个活动ak的增添则有很多情况,如图3所示。图3a和图3c是新增了具有严格序关系的活动,图3b是新增了具有交叉序关系的活动,图3d是新增了具有排他序关系的活动,插入操作具体的修复步骤见算法6。
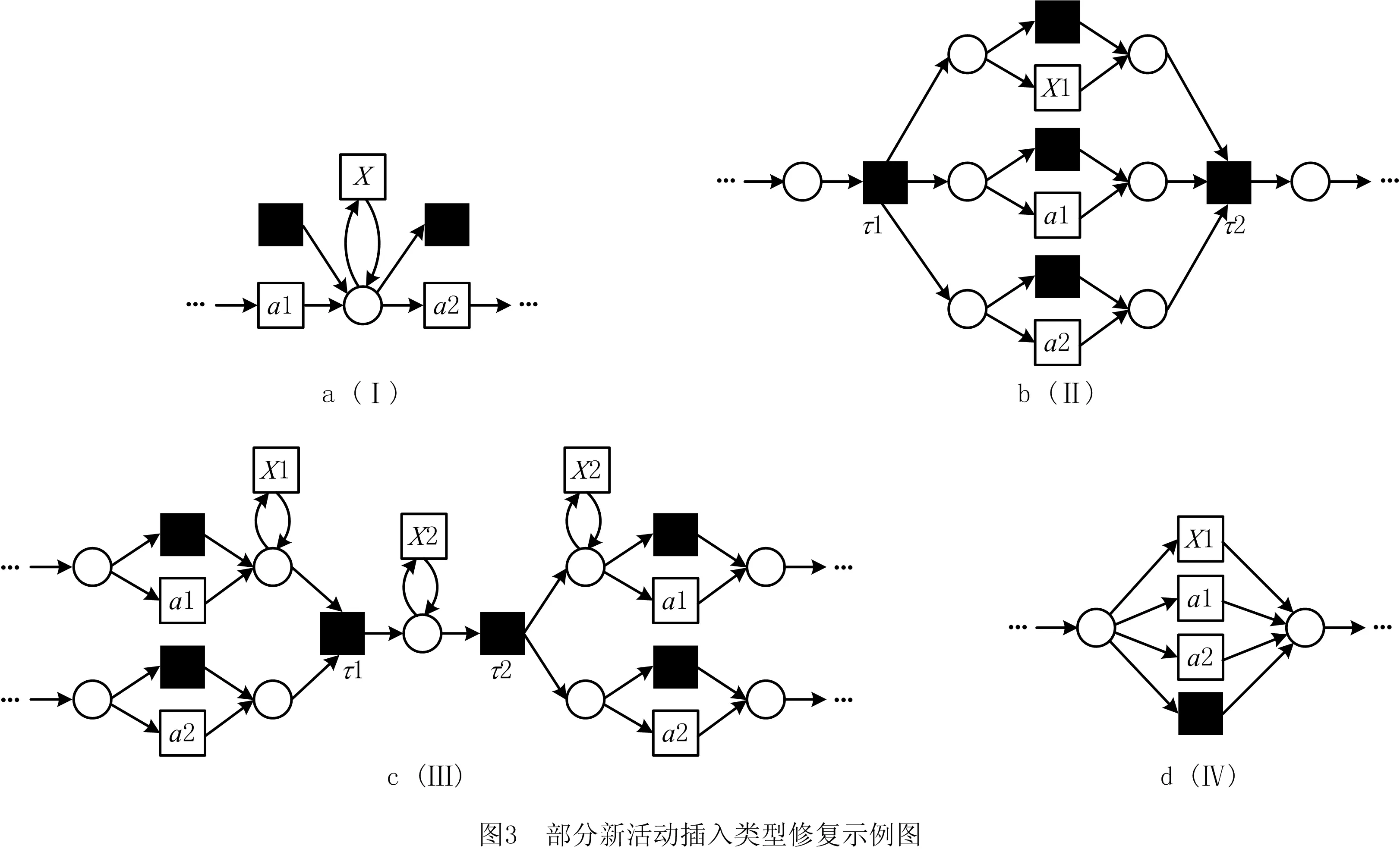
算法6中,一个新活动的添加会使系统实际日志中出现与该活动相关的严格序和交叉序关系。其中第3~10行对图3a和图3c中X和X2类型结构进行了修复;第11~13行修复了图3c中X1类型结构;第14~16行可对图3c中X3类型结构进行修复;第17~21行对图3b类型结构进行了修复;22~23行可对图3d类型结构进行修复。
对于移动活动的修复大体采用先调用delete修复后insert修复以达到move修复的效果,例如图4中前两种类型,然而对于两个活动间排他关系移动为交叉序关系的情况,正如图4中类型的修复是通过添加一个循环隐变迁从而使得活动a1和a2之间存在交叉序行为。具体的move操作模型修复步骤如算法7。
算法6基于不完备日志偏差域的模型Insert操作修复算法。
输入:insert日志偏差域Gk,活动集Ains,Ains对应的1-pred和1-succ集以及Petri网N1=(P1,T1,F1);
输出:修复后的Petri网N2=(P2,T2,F2)。
1. for each ak∈Gkdo
2.调用算法3,得到其对应的活动对(ai,ak),(ak,aj)
3. for each ax∈1-pred(ak) and ay∈1-succ(ak) do//ax为新增活动ak直接前继中的元素
4. if Ract(ax,ak)=1 and Ract(ak,ay)=1 then Get(ax,px),(py,ay)∈F
5. //px,py为网N中对应的库所
6. if px=pythen T2=T1∪{ak},F2=F1∪{(px,ak),(ak,px)}
7. else if |1-pred(ak)|≥2 and each ax1,ax2∈1-pred(ak),Ract(ax1,ax2)=2
8. then Get(ax1,px1),(px1,τxo),(τxo,pk)∈F1,T2=T1∪{ak},F2=F1∪{(pk,ak),(ak,pk)}
9. else if |1-succ(ak)|≥2 and each ay1,ay2∈1-succ(ak),Ract(ay1,ay2)=2
10. then Get(py1,ay1),(τyi,py1),(pk,τyi)∈F1,T2=T1∪{ak},F2=F1∪{(pk,ak),(ak,pk)}
11. for each ax1,ax2∈1-pred(ak) do//ax1,ax2为新增活动ak直接前继中的元素
12. if Ract(ax1,ak)=2 and Ract(ax2,ak)=1 and Ract(ax1,ax2)=2
13. then Get(ax2,px2)∈F1,T2=T1∪{ak},F2=F1∪{(px2,ak),(ak,px2)}
14. for each ay1,ay2∈1-succ(ak) do//ay1,ay2为新增活动ak直接后继中的元素
15. if Ract(ak,ay1)=2 and Ract(ak,ay2)=1 and Ract(ay1,ay2)=2
16. then Get(py2,ay2)∈F1,T2=T1∪{ak},F2=F1∪{(py2,ak),(ak,py2)}
17. for each ax1,ax2∈1-pred(ak) and each ay1,ay2∈1-succ(ak) do//同上意义
18. if Ract(ax1,ak)=Ract(ak,ay1)=2 and Ract(ax2,ak)=Ract(ak,ay2)=Ract(ax1,ax2)=Ract(ay1,ay2)=2
19. then Get(px1,ax1),(τi,px1),(ay1,py1),(py1,τo)∈F1,T2=T1∪{ak},P2=P1∪{pi,po},
20. F2=F1∪{(ti,pi),(pi,τnew),(pi,ak),(τnew,po),(ak,po),(po,to)}
21. //其中ti,to可能为可见变迁,也可能为隐变迁
22. if ∃ac∈A,Ract(ac,ak)=0 and ∃ax∈1-pred(ak),Ract(ax,ac1)=1 and ∃ay∈1-succ(ak),Ract(ac2,ay)=1
23. then Get(pi,ac1),(ac2,po)∈F1,T2=T1∪{ak},F2=F1∪{(pi,ak),(ak,po)}
24. end for
25. return N2=(P2,T2,F2)
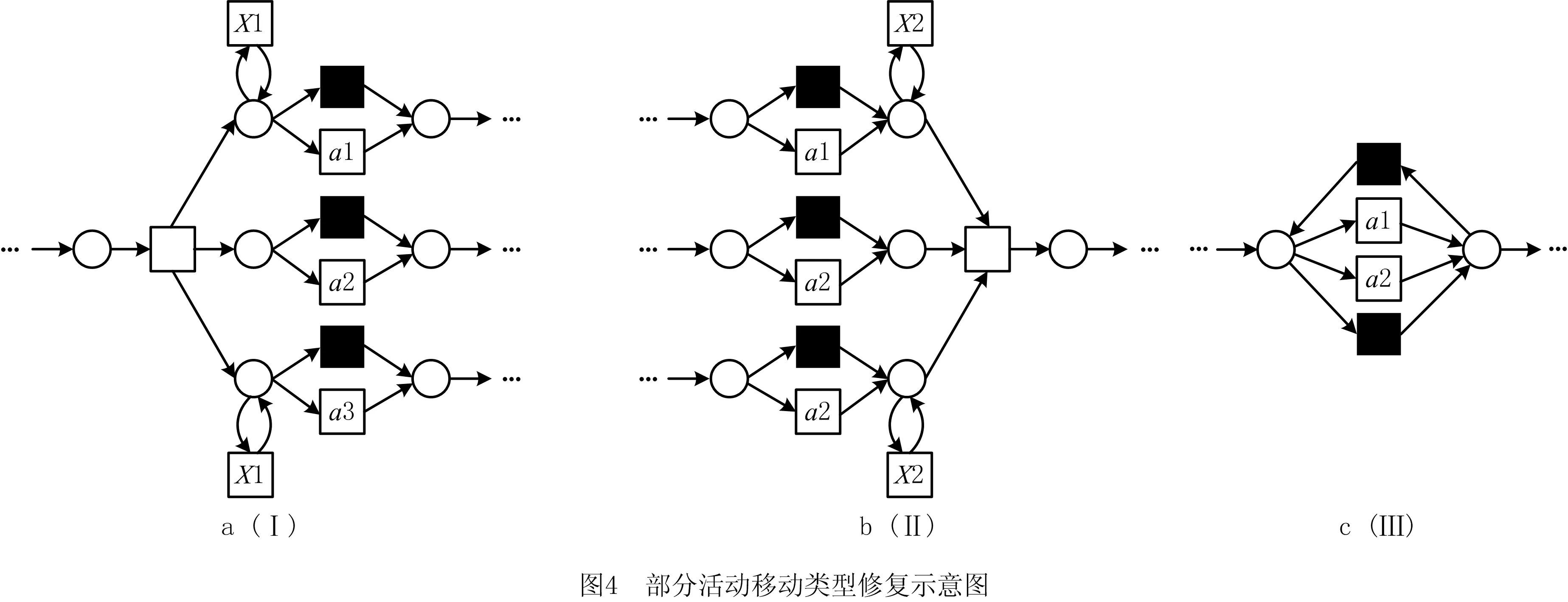
算法7基于不完备日志偏差域的模型move操作修复算法。
输入:move日志偏差域Gm,活动集Amov,Amov对应的1-pred和1-succ集以及Petri网N2=(P2,T2,F2);
输出:修复后的Petri网N′=(P′,T′,F′)。
1. Az=∅
2.for each am∈Gmdo Az=1-pred(am)∩1-succ(am)
3.if Az≠∅
4.for each az∈Azdo
5.if Rhis(am,az)=0 and Ract(am,az)=2
6. then Get(pi,am),(am,po)∈F2,T′=T2∪{τm},F′=F2∪{(po,τm),(τm,pi)},Gm=Gm-am-az
7. else调用算法5,调用算法6,Gm=Gm-am
8. else调用算法5,调用算法6,Gm=Gm-am
9. return N′=(P′,T′,F′)
5 业务系统模型修复案例分析
5.1 基于日志偏差域的修复算法的时间复杂度分析
在本文提出的7个算法中,算法1的时间复杂度为O(|σ|),其中σ指事件日志L中所有的迹数量;算法2的时间复杂度为O(|T|2),|T|相当于活动集A中所有活动的个数;算法3、算法4和算法5的时间复杂度均为O(n);算法6和算法7的时间复杂度为O(n·max(|1-pred(a)|,|1-succ(a)|)),其中:|1-pred(a)|表示活动a的直接前继的个数,|1-succ(a)|表示活动a的直接后继的个数。
5.2 医疗实验案例分析
5.2.1 实验模型和数据
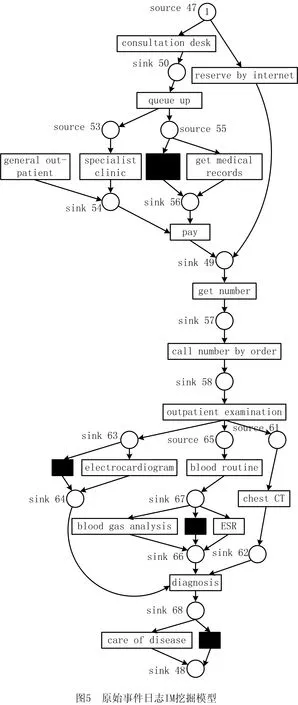
实验中使用的数据来自青岛一家医院。以医院的胸外科手术为例,利用Prom工具中的演绎挖掘机(Inductive Miner,IM)挖掘原始系统的不完备事件日志,可以得到一个模型,如图5所示。首先,患者在医院挂号有两种方式:互联网预订;先询问咨询台,其次准备排队挂号,排到时工作人员会问及其之前的医疗诊断,同时需确定是专家还是普通门诊,然后支付挂号费,然后患者会收到一个号码并等待叫号。当患者需要门诊检查时,可能会检查胸部CT,并进行心电图检查,常规,红细胞沉降率(Erythrocyte Sedimentation Rate,ESR)或血气分析同时进行。最后医生会根据结果诊断检查并开始治疗。
实际过程中可能存在某些情况。例如,对于某些大城市在挂号后会根据放号的范围在就诊前进行排队;或当病人做一个门诊检查,需要创建一个新的检查,如胃镜;或病人需要血液常规检查后同时进行ESR和血气分析;或对病人进行一个生物全套检查。
随着实际医疗过程的变化,系统实际的事件日志出现的如上新事件的添加和旧事件的删除或移动,使得原始事件日志挖掘出的模型不能重放其对应的变迁。为了解决因insert、delete和move变化操作引起的行为不一致问题,从医院系统获得8个事件日志(L1~L8),上述所有更改都记录在这些日志中。在手动删除严重偏离原始模型的事件日志后,日志中包含的迹从200到900不等,实验数据集中的迹、事件、活动的数量和迹的长度范围如表1所示。
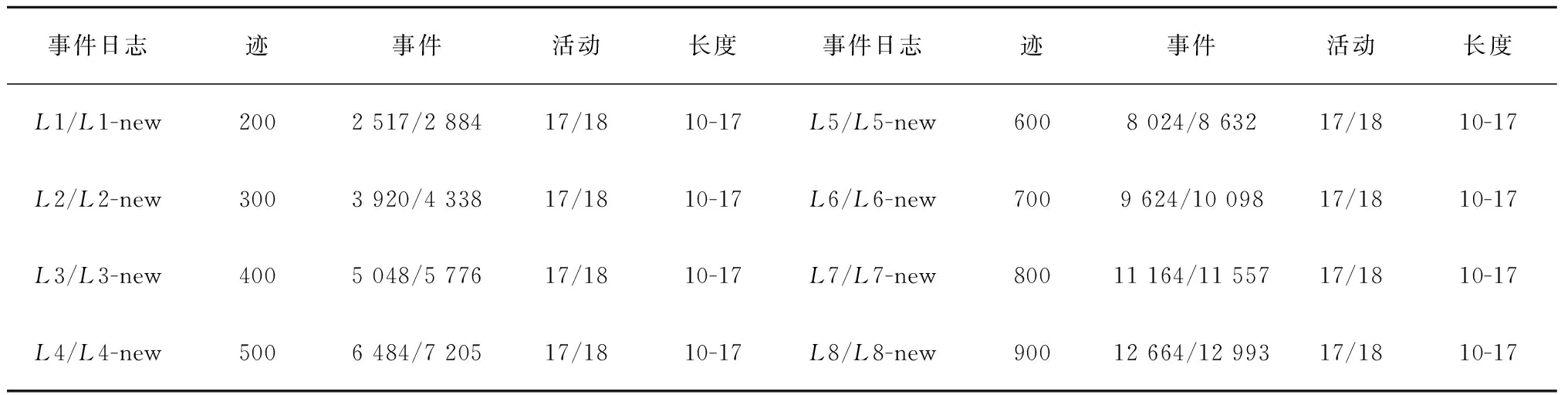
表1 实验中日志的详细信息
5.2.2 三种修复方法的模型修复实验
图5是根据表1中日志L1-L8得到的演绎挖掘模型,而图6是根据表1中日志L1-new-L8-new得到的演绎挖掘模型,可以看出图5和图6存在结构上的差异。
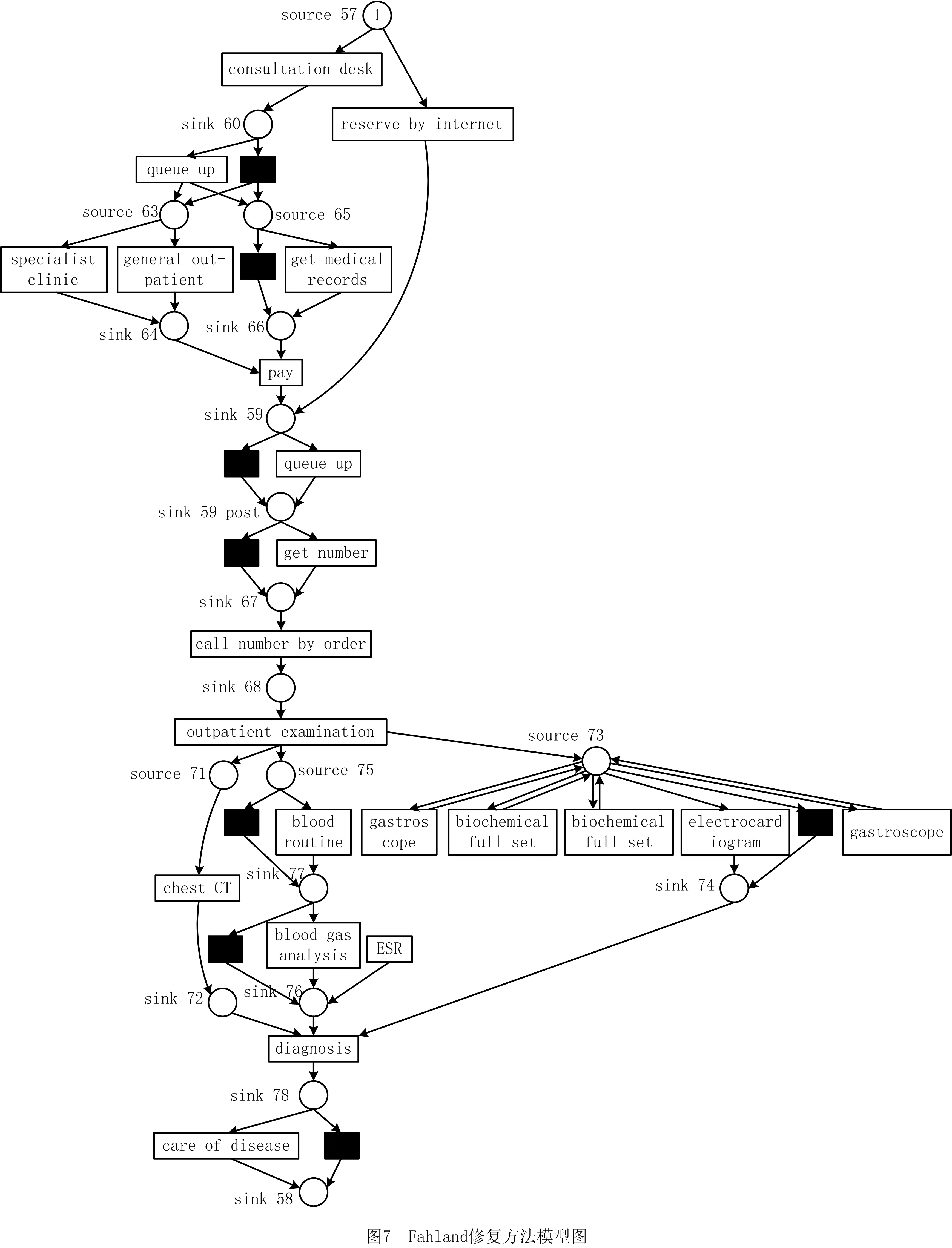
本节利用Fahland方法,Goldratt方法以及本文方法来修复图5中的模型,如图7、图8和图9所示。由于表1中日志L1-new包含最全面的迹,因此将L1-new作为模型修复的实验数据。
图7中Fahland修复模型的方法是基于给定事件日志和原始模型之间的最佳对齐方式获得偏差。根据日志中的移动以最佳对齐方式收集子日志;然后挖掘相应的子过程并将其以自循环的形式添加到原始模型中。对于事件日志中属于不同选择分支的活动,该方法可以根据对齐方式查找偏差;然后添加不可见变迁和子过程以修复原始模型。然而在图7中可直观地发现Fahland模型修复方法不能重放活动blood gas analysis和ESR之间的交叉序关系。
图8中Goldratt修复模型的方法根据某些约束向模型中添加了一个单独的变迁作为自循环或不可见变迁。对于包含不同选择分支上活动的事件日志,此方法在原始模型中插入不可见变迁和自循环以重放以上事件日志。
本文修复模型的方法是基于不完备日志的变化检测方法,利用活动的比较矩阵对事件日志的Insert、Delete和Move变化操作进行描述,从而发现原始事件日志同系统实际日志的偏差域,根据日志偏差域对原始事件日志发现的模型进行修复。实验中原始事件日志和实际事件日志数据中所有活动的简记符号如表2所示。

通过调用算法1、算法2、算法3和算法4得到的实验中原始事件日志和实际日志的偏差域如下所示:
(1)删除活动相关的日志偏差域:(A,H),(B,H),(C,H),(D,H),(E,H),(F,H),(G,H),(H,I),(H,J),(H,K),(H,L),(H,M),(H,N),(H,O),(H,P),(H,Q),(H,R),(H,S)。
(2)新增活动相关的日志偏差域:(A,K),(B,K),(D,K),(E,K),(F,K),(G,K),(H,K),(I,K),(J,K),(L,K),(M,K),(N,K),(O,K),(P,K),(Q,K),(K,L),(K,M),(K,N),(K,O),(K,P),(K,Q),(K,R),(K,S),(A,M),(B,M),(D,M),(E,M),(F,M),(G,M),(H,M),(I,M),(J,M),(K,M),(L,M),(M,K),(M,L),(M,N),(M,O),(M,P),(M,Q),(M,R),(M,S)。
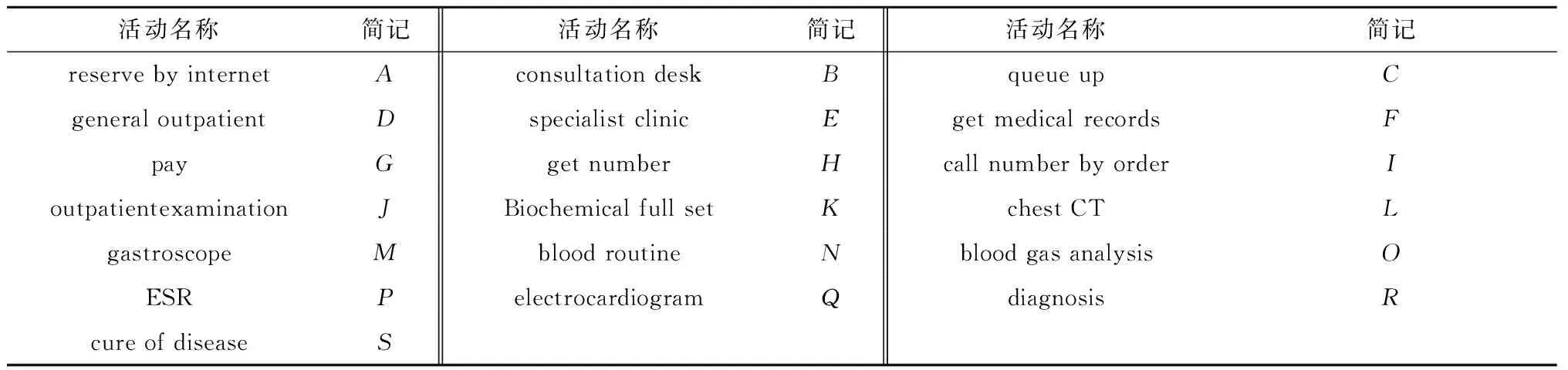
表2 日志中活动名称简记表
(3)新增活动相关的日志偏差域:(C,D),(C,E),(C,F),(C,G),(C,H),(A,C),(D,C),(E,C),(F,C),(G,C),(O,P),(P,O)。其中行为关系发生变化的活动的集合即变化集为CS={A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S}。
由定义5可知实验数据中实际事件日志活动的直接前继和直接后继如表3所示。
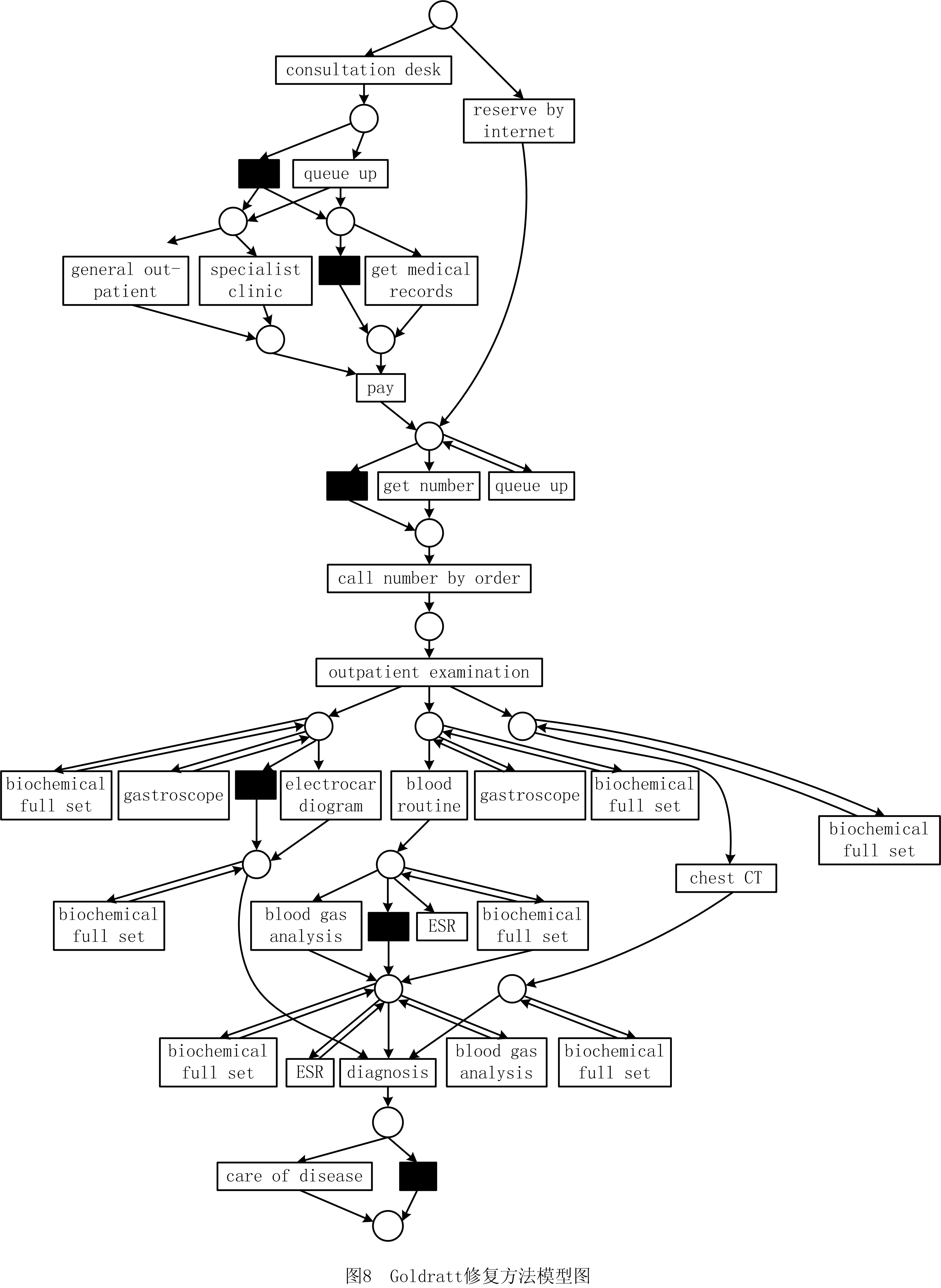
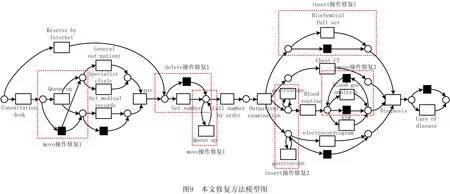
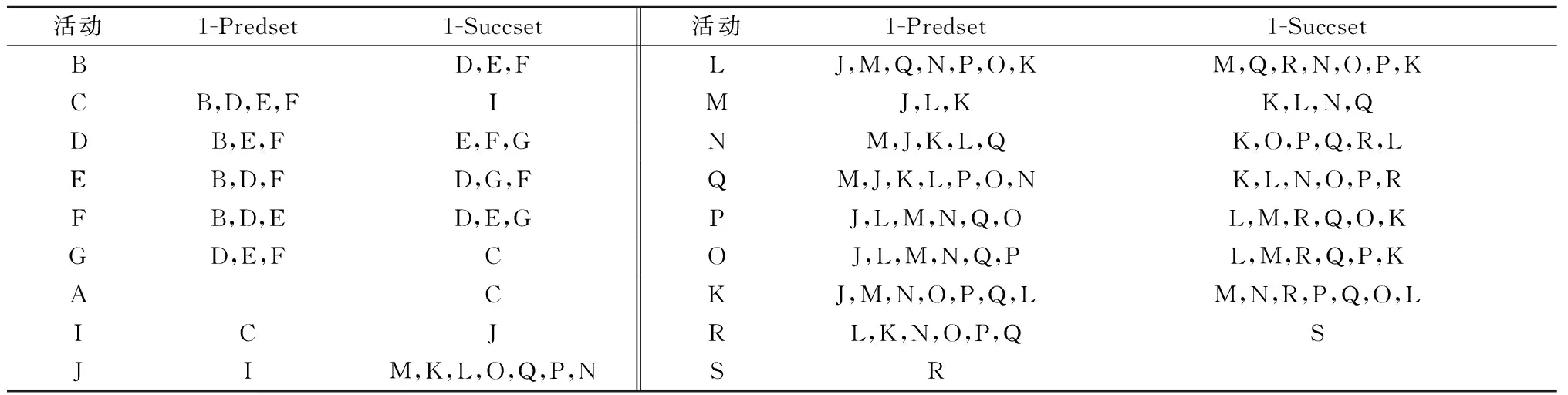
表3 实际日志中各活动的直接前继和直接后继
经过算法4、算法5、算法6和算法7的运行与分析,可得如下结论:
(1)Delete变化操作的修复:根据上述被删除活动的日志偏差域,可知实验案例中H为删除的活动。由于图5中没有隐变迁能使其跳过,因此需添加一个隐变迁使实际日志迹能在原始事件日志挖掘出的模型中重放,可从图9中的delete操作修复1观察到修复结果。
(2)Insert变化操作的修复:根据表3及新增活动的日志偏差域,可知实验案例中K,M为新增活动。由于活动K的直接前继和直接后继分别为{J,M,N,O,P,Q,L}和{M,N,R,P,Q,O,L},算法6中的17~21行代码对其进行修复,并知K同活动M,N,O,P,Q,L均为交叉序关系。但满足算法6中第18行代码条件的仅活动L和Q,19~20代码的运行可对其进行修复,在图9中的insert操作修复1可观察到修复结果,对应图3b的情况。
表3中活动M的直接前继和直接后继分别为{J,L,K}和{K,L,N,Q},算法6中的14~16行代码对其进行修复。在实际事件日志中,由于活动M的直接后继中活动L和K同M均为交叉序关系,活动N和Q同M均为严格序关系,又因为活动L和K为交叉序关系,因此可以根据活动L或活动K执行第16行代码对图5中的模型进行修复,图9中的insert操作修复2观察到修复结果,对应于图2c中X3的情况。
(3)Move变化操作的修复:根据表3及移动活动的日志偏差域,可知实验案例中C,O和P为移动的活动。活动C的直接前继和直接后继分别为{B,D,E,F}和{I},由于活动C的直接前继和直接后继交集为空,算法7中的第9行代码的执行可对其进行修复,在图9中的move操作修复1观察到修复结果。
表3中活动O的直接前继和直接后继分别为{J,L,M,N,Q,P}和{L,M,R,Q,P,K}。由于活动O的直接前继和直接后继交集非空,而且活动O和P在原始事件日志中Rhis(O,P)=0,在实际日志中的行为关系为交叉序关系Ract(O,P)=2,因此算法6中第7行代码对其进行修复,在活动O和P的前继库所和后继库所间添加一个可循环的隐变迁,以此使其之间的交叉序关系得以重放,可从图9中的move操作修复2观察到修复结果。仿真结果与本文所述方法计算结果一致,进一步验证了方法的正确性。
5.2.3 模型评估
以表1中的8个事件日志L1-new~L8-new为例,将本文方法与Fahland和Goldratt两种模型修复方法从适合度、精确度和简单性3个方面进行比较。根据文献[24]中提供的公式来计算事件日志和修复模型之间的适合度和精确度。
图10显示了3种模型修复方法的适合度和精确度的比较结果。 适合度是评估过程模型质量的最重要指标。 如果模型可以重放事件日志中的活动,则该模型具有良好的适合度。 即如果一个模型可以重放事件日志中的所有迹,则该模型的适合度为1。由图10a可以看出,在不同数量的事件日志下,本文方法的适合度较高,其次为Fahland和Goldratt模型修复方法。
精确度是指在过程模型中不允许发生事件日志中无法观察到的活动。从图10b可以看出,随着事件日志中跟踪数量的增加,精度值不会发生太大变化。 在不同数量的事件日志中,由于重复变迁或自环可能会降低修复模型的精确度,本文方法具有比其他两种方法更高的精确度。
简单性意味着修复的模型应尽可能简单。为了比较这3种模型修复方法的简单性,统计了各修复模型中的主要标准:添加的库所数、变迁数|T+τ|、弧数和重复变迁数,如表4所示。Fahland方法添加的库所数、变迁数|T+τ|、弧数和重复变迁数分别为1,9,19和3;Goldratt方法添加的库所数、变迁数|T+τ|、弧数和重复变迁数分别为0,14,28和10;本文方法添加的库所数、变迁数|T+τ|、弧数和重复变迁数分别为2,8,18和2;因此本文模型修复方法的简单性更好些。由上述分析可知,本文方法在适合度、精确度和简单性这3个方面具有较好的结果,由此可以证明本文方法的有效性和正确性。
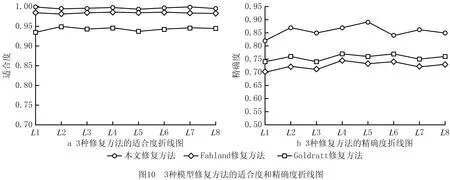

表4 四种模型简单性表
5.3 结果分析
本文通过日志偏差域、实际系统日志的直接前继和后继来进行模型的修复,最后使得原始事件日志和系统实际日志均能在修复后的模型中回放可行迹。然而,本文是基于日志中所有活动都不考虑隐变迁的发生情况进行变化检测分析。因为对于与某活动具有排他关系的隐变迁可能会导致该活动的发生权被剥夺,但并没有执行删除该活动的变化操作。所以,本文方法修复的模型也存在不能重放的迹,如实验中活动blood routine的跳过在图9中无法执行,但相比Fahland和Goldratt模型修复方法还是具有较好的适合度,精确度和简单性。同时当某系统的原始事件日志缺失时,还可利用本文方法修复的模型同修复前的模型进行对比,以寻找到原始事件日志的大多数可行迹。
6 结束语
事件日志中活动的变化将导致模型中变迁行为关系的改变,大多数研究人员的前提都是基于完备日志进行原始模型的修复,然而如何基于不完备日志进行变化检测和模型修复同样是一个有价值的研究课题。本文在现有研究基础上,利用不完备日志中变迁活动的偏差域以及系统实际日志中活动的直接前继和后继来确定变化的活动和变化后活动的位置,根据变化的活动及其变化后活动的位置实现模型的修复,并通过Prom工具对所提出方法的正确性和有效性进行了分析验证。
在今后的工作中,重点研究更为高效的不完备日志变化检测技术与模型修复方法,以及基于不完备日志的局部活动集所对应的模型修复问题,而不再是单个活动的变化。同时,基于不完备日志模型的相似度问题也有待解决。
