基于神经网络的矫直机压下量自学习控制系统*

2021-10-11尉建龙

机械工程与自动化 2021年5期

尉建龙

(太原重工股份有限公司技术中心矿山采掘装备及智能制造国家重点实验室，山西太原 030024)

0 引言

辊式热矫直机是钢铁企业中板材生产线上很重要的生产设备，随着国家在战略层面对智能化的规划，钢铁企业也需要进行智能化的升级改造。压下量模型是实现精确矫直过程自动化的关键技术，在原有模型上增加智能化算法，即增加自学习模型管理模块，改善模型，以达到矫直机压下量的自适应控制。智能控制的设计方法有专家系统、模糊控制、神经网络和遗传算法，其中神经网络算法具有自学习和自适应的典型特点，具有较强的自适应能力，不依赖模型。板材矫直过程是非线性、多变量耦合的不确定过程，因此采用神经网络算法对矫直过程进行自适应控制，相比其他控制算法具有天然的优势。

1 矫直机压下量工艺模型

矫直机工艺模型主要依据材料变形的物理学原理，在接收到轧线二级计算机传输的板坯数据后，根据设备设计载荷及约束条件完成辊缝、压下量、矫直速度、矫直力等参数的设定计算。

板坯初始数据主要有板坯编号(ID)、钢种、板坯厚度、板坯宽度、板坯入口前测量温度、板坯速度、钢级和板坯条件等。矫直机的设备数据(几何尺寸、机架刚度等)存储于矫直机模型的数据库/数据表中。

矫直机工艺模型计算流程如图1所示。

图1 矫直机工艺模型计算流程

以十一辊矫直机为例，经过现场验证，入口与出口矫直辊的压下量即第二辊(上排辊)、第三辊(下排辊)与第十辊压下量[1-3]计算公式分别为：

(1)

(2)

(3)

其中：K为通过试验得到的修正系数；K′为系数，根据原始曲率的大小可具体确定数值;(0～1)具体值的选取根据原始曲率的大小查询相应的经验值；σs为板材屈服强度；l为矫直辊辊距；E为板材的弹性模量；h为板材厚度。

当入口与出口矫直辊的压下量确定后，上排其余各矫直辊的压下量为：

(4)

其中：t为常数，随着i取值变化而变化，i=4,6,8,t=3,2,1。

尽管下排辊的位置不变，但板材矫直过程在经过下排辊时同样会产生弯曲及挠度，因此下排辊具有相对压弯量。下排辊的相对压弯量为:

(5)

2 基于神经网络的自学习模型实现

通过神经网络算法建立自学习模块，形成压下量自学习控制系统。神经网络通常由输入层、隐藏层、输出层、损失层几部分组成。在训练神经网络的过程中，若预测正确，来自于损失层的反馈会强化产生该预测结果的激活路径；若预测错误，则错误会沿着路径逆向返回，这条路径上神经元的激活条件就会被重新调整，以减少错误。

钢种为Q235，板坯厚度为75 mm，板宽为4 200 mm，屈服应力为35 MPa，弹性模量为100 000 MPa，残缺程度为中度(B级)的矫直机压下量34组实测数据如表1所示。

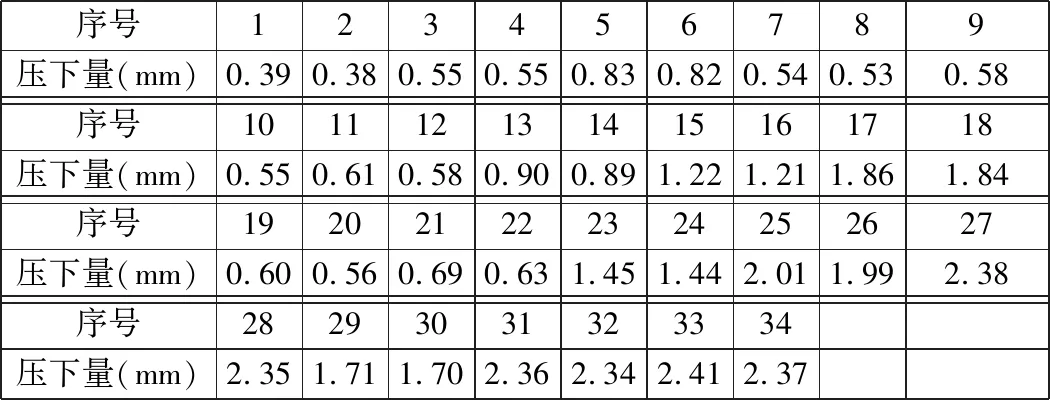
表1 矫直机压下量实测数据

首先创建一个多层神经网络，采用S形激活函数，其中输入层采用1个神经元，输出层采用1个神经元，隐含层采用16个神经元。实现过程为：network_ AdjRoll=new ActivationNetwork(new BipolarSigmoidFunction(3),1,16,1)。

然后创建BP神经网络进行训练，实现过程为：teacher_ AdjRoll =new BackPropagationLearning(network_AdjRoll)。

最后设置学习率和冲量系数，实现过程为：teacher_AdjRoll.LearningRate =0.05;teacher_AdjRoll.Momentum=0。

对初始数据进行神经网络训练，生成压下量训练数据，C#语言代码如下：

StreamWriter train_AdjRoll =new StreamWriter("训练数据(压下量).txt");

{

string temp =null;

temp +=iniYearData_AdjRoll[i + j].data + ' ';

train_AdjRoll.WriteLine(temp);

}

train_AdjRoll.Close();

{

trainInput_AdjRoll [i][0] =premnmx(trainInput_AdjRoll[i][0],min_AdjRoll,max_AdjRoll);

trainOutput_AdjRoll[i][0] =premnmx(trainOutput_AdjRoll[i][0],min_AdjRoll,max_AdjRoll);

}

使用C#语言实现基于神经网络的矫直机压下量自学习控制系统，采用神经网络算法训练数据进行测试。在初始训练过程中我们发现：压下量的预测值与实际值之间的误差波动还是偏大，随着训练次数的增加，误差值波动已经很小，基本达到了预期的训练要求。软件实现前台显示界面如图2所示，包括对网络的训练以及测试网络的过程。

图2 软件实现前台显示界面

在矫直过程中，模型具有自学习功能，并根据现场实测数据进行设置参数的动态优化，提高了矫直效果。

自学习功能的建立实现了矫直机系统自适应调整功能，大大降低了操作人员的劳动强度，具有调整精度高、速度快的特点，满足了现场的工艺要求，同时提高了矫钢的速度和成材率，并降低了设备的设备率；使矫直机区域各控制设备的运行参数更优化、效率更高、设备运转更安全，对今后矫直机自动化控制系统的设计、应用和技术改进都有非常重要的意义[4-6]。