五自由度磁力驱动平台的设计与仿真分析*

王韬宇，孙 凤，张 明，李 强，徐方超，赵海宁

(沈阳工业大学 机械工程学院，辽宁 沈阳 110870)

0 引言

磁力驱动技术因其响应快、无接触摩擦无需润滑、易于实现结构紧凑及多自由度运动等优势受到国内外广泛关注，并取得了许多研究成果。中南大学的陈启会等[1]设计了一种平面型的磁悬浮驱动平台，驱动单元采用差动控制，不仅提供了控制灵敏性，还保证了系统具有一定的刚度。李群名等[2]通过对平台的机电耦合动力学模型进行运动稳定性分析,得到了平台实现稳定悬浮时控制参数范围，并通过实验验证了此范围内平台系统在稳定悬浮时具有良好的动、静态性能。以色列Ben-Gurion大学的学者们研制了一种六自由度精密定位台，平台由三组横向磁组和三组垂向磁组组成，可以实现0.4 mm的平动行程和±1.2 μrad的转动行程[3]。青岛理工大学的武倩倩等[4]设计了一种六自由度的磁悬浮隔振平台，并提出了双闭环的控制策略，使系统在低频到中高频带内实现隔振控制，在极低频带内实现跟踪控制。沈阳工业大学的鲁煜莹等[5]对磁悬浮直线同步电机进行研究，建立了系统数学模型，并通过仿真分析，证明了磁悬浮系统具有较好的抗干扰能力。

本文提出了一种紧凑型五自由度磁力驱动平台，采用6组差动电磁铁实现五自由度的运动。对五自由度磁力驱动平台进行了数学建模，通过PID控制对平台系统进行仿真分析，证明了平台能够实现稳定悬浮。

1 磁力驱动平台的结构设计及工作原理

五自由度磁力驱动平台的结构如图1所示，该平台主要由上顶盖、下底盖、连接环、电磁铁、浮动平台等组成。

五自由度磁力驱动平台整体采用主动磁悬浮轴承的结构，使结构更加紧凑；电磁铁采用差动的工作方式进行驱动，以提高系统响应速度及控制精度。平台整体主要由上顶盖、下底盖及中间起连接作用的连接环组成。其中在上、下盖上均匀分布着4组差动电磁铁(轴向电磁铁)，可以使浮动平台实现Z轴方向的运动和绕X、Y轴的翻转运动。其中，Z轴方向的运动由4组电磁铁共同驱动，绕X轴翻转运动由Y轴方向的2组电磁铁驱动，绕Y轴翻转运动由X轴方向的2组电磁铁驱动；中间部分的连接环上同样均匀分布着2组差动电磁铁(径向电磁铁)，与X轴和Y轴呈45°角的关系，2组电磁铁共同驱动可以实现浮动平台X、Y轴方向的运动。浮动平台的位置检测共由5个位移传感器来完成，其中上顶盖上安装的3个位移传感器用来检测Z轴方向的运动和绕X、Y轴的翻转运动；连接环处安装的2个位移传感器用来检测X、Y轴方向的运动。

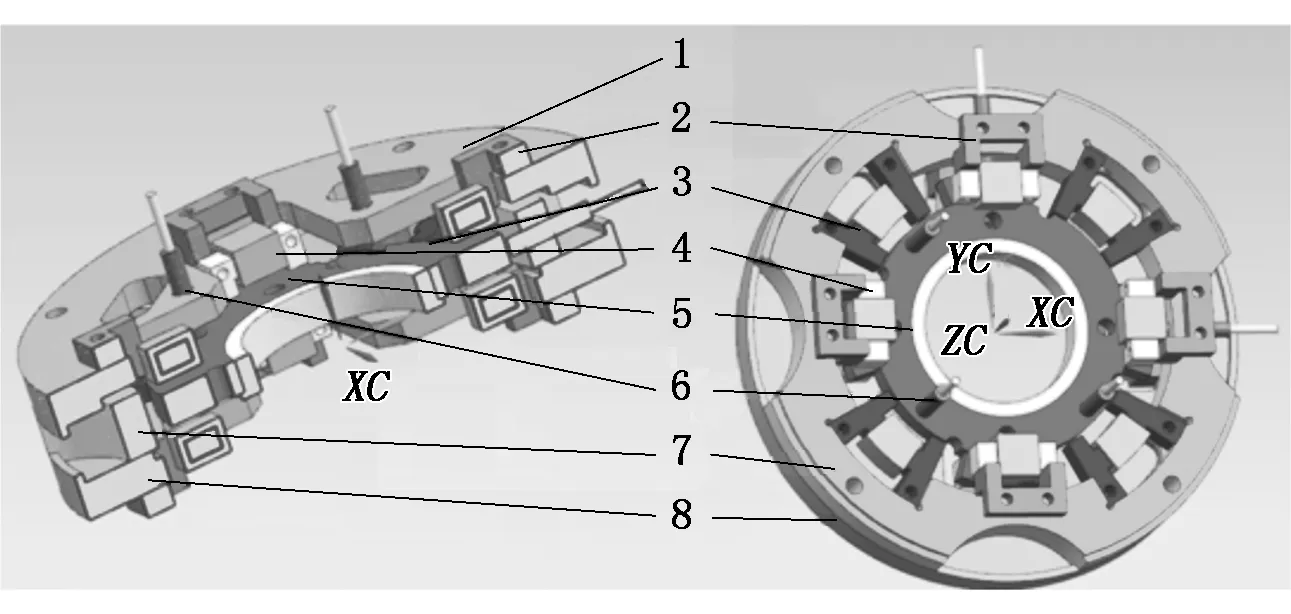
1-上顶盖；2-磁铁连接块；3-径向电磁铁；4-轴向电磁铁；5-浮动平台；6-位移传感器；7-连接环；8-下底盖

2 系统动力学模型建立

系统受力分析如图2所示，其中Fz1～Fz4表示平台受到的4组差动电磁铁的电磁力。根据系统的结构，设定平衡位置时的坐标系为绝对坐标系，此时浮动平台的质心为O点；当平台受到电磁力作用产生运动时，设运动时的坐标系为相对坐标系，此时平台质心为O′点。设定传感器气隙变小的方向为正。

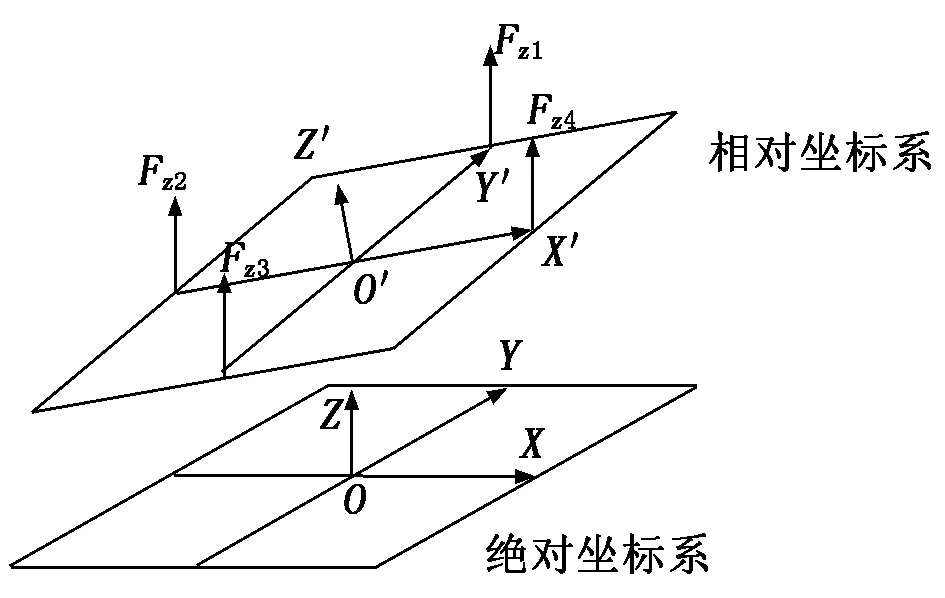
图2 系统受力分析

设O点的广义坐标为：

O=[xyzαβ]T.

(1)

其中：x、y和z表示平台平动上的自由度；α和β分别表示平台绕X轴和Y轴运动的自由度。平台在运动时所处的坐标系O′相对于6组电磁铁的坐标可以表示为：

O′=[z1z2z3z4x1x2y1y2]T.

(2)

其中：z1、z2、z3和z4表示垂直方向电磁铁的自由度；x1、x2、y1和y2表示水平方向电磁铁的自由度。两坐标系的转换关系为：

(3)

其中：a为电磁铁到平台质心的距离。

根据差动电磁铁原理可知，当平台在平衡位置时，则有：

(4)

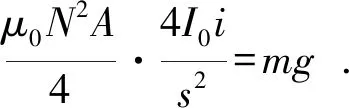
其中：F为平台受到的合力；F1为平台受到的上电磁铁的力；F2为平台受到的下电磁铁的力；μ0为真空磁导率；N为线圈匝数；A为电磁铁有效磁面积；I0为偏置电流；i为控制电流；s为悬浮气隙；m为悬浮平台的质量；g为重力加速度。

当平台在平衡位置受到扰动而产生位移e，此时两对电磁铁产生的合力为：

(5)

其中：i0为平台平衡时的控制电流。

将式(5)在平衡位置进行线性化，即当i=0，e=0时线性化得：

F=Ki·i+Ks·e.

(6)

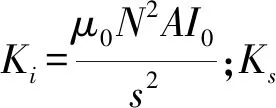
系统的总动能分为平动动能T1和转动动能T2，分别为：

(7)

其中：Jα为平台绕X轴旋转的转动惯量；Jβ为平台绕Y轴旋转的转动惯量。利用拉格朗日方程得到系统的动力学模型为：

.(8)

其中：i1～i6分别为6组差动电磁铁的控制电流。

根据动力学方程建立系统状态空间矩阵：

(9)

其中：v为系统的状态；u为系统输入，即控制电流；w为系统的输出。

设

.(10)

求得出：

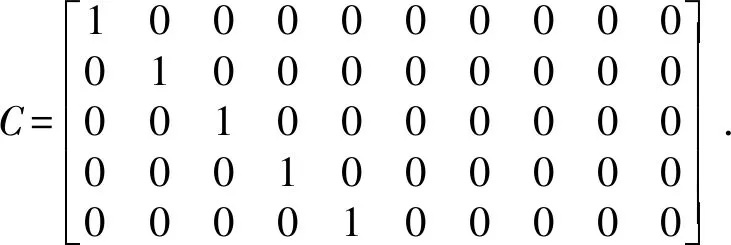
3 控制系统搭建

图3为系统控制原理图。其中，xd、yd、zd、αd和βd为系统的期望值，与受控平台反馈回的值进行比较，将误差值输入控制器中得到控制律，对平台进行控制。

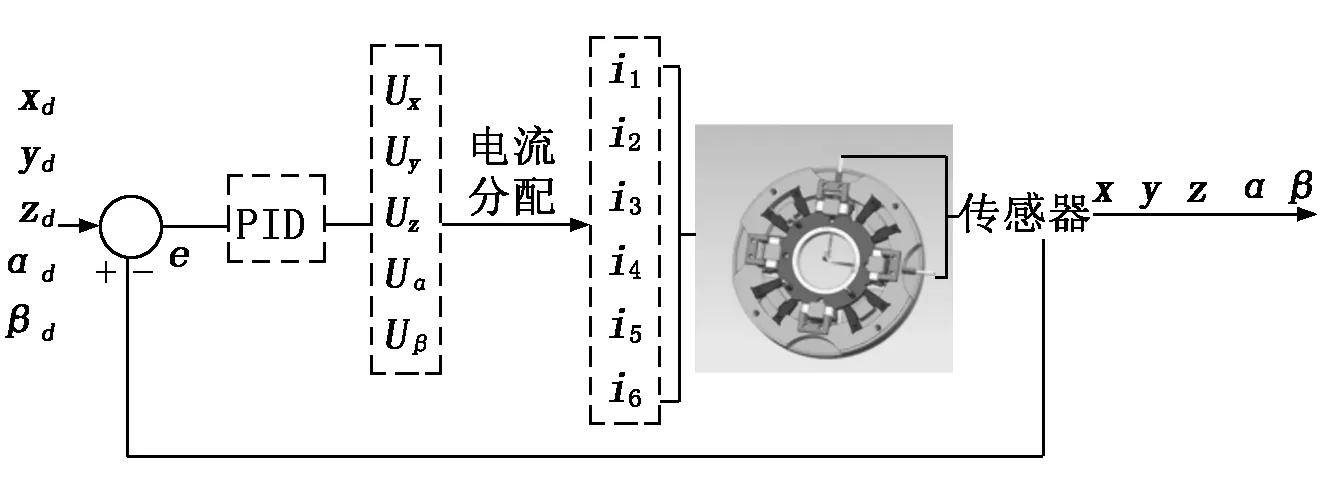
图3 系统控制原理图

由式(10)可知系统是一个6输入5输出的过驱动系统，为了方便控制器的搭建，所以需要对此进行改变，即：

(11)

其中：Ux、Uy、Uz、Uα和Uβ为系统设置的虚拟控制量。这样就使系统变为5输入5输出的系统，但是系统实际需要的是6个控制量，所以控制器输出的虚拟控制量需经过电流分配环节得到系统实际需要的控制量。电流分配环节实际是对虚拟的控制量进行权重分配，如式(12)：

(12)

综上所述，控制器输出的控制量经过再分配得到6组差动电磁铁的控制电流之后输入到受控模型中，实现平台5个自由度的运动控制。

4 仿真分析

利用Simulink对系统进行仿真，分析其在各个自由度上的控制效果。在0.5 s时给X、Y和Z向运动值为0.1 mm的阶跃信号，给绕X轴和Y轴翻转运动值为0.005 rad的阶跃信号，并确定各个自由度的控制参数分别为：X轴方向运动控制参数：kp=8 500，ki=50 000，kd=100；Y轴方向运动控制参数：kp=8 500，ki=50 000，kd=100；Z轴方向运动控制参数：kp=18 000，ki=80 000，kd=100；绕X轴翻转运动控制参数：kp=600，ki=15 000，kd=3；绕Y轴翻转运动控制参数：kp=600，ki=15 000，kd=3。

系统各自由度的位移响应如图4所示。对于平动运动，以X轴方向运动为例，当系统在0.5 s接收到指令开始运动时控制电流先迅速增大并达到瞬时最大值；此时悬浮平台位移达到最大值；随着系统的调整，控制电流减小，最终达到稳定值，此时悬浮平台也由位移最大值调整到目标期望值，达到稳定悬浮状态。并且由图4(a)、(b)和(c)可以分析得到系统响应迅速，稳态误差为0，其中沿X轴方向运动系统的超调量为80%，响应时间为0.3 s；沿Y轴方向运动系统的超调量为80%，响应时间为0.3 s；沿Z轴方向运动系统的超调量为75%，响应时间为0.45 s。对于转动运动的2个自由度，以绕X轴翻转为例，当系统在0.5 s接收到指令开始运动时，控制电流的变化趋势为先增大再减小最终达到稳定值。并且由图4(e)、(d)分析得到系统响应迅速且稳态误差为0，其中绕X轴翻转系统的超调量为70%，响应时间为0.1 s；绕Y轴翻转系统的超调量为70%，响应时间为0.1 s。对于各个自由度位移响应超调量大的原因通过分析有两点：首先系统本身为无阻尼系统，在上升期间会存在超调；其次在控制参数的调节上满足了响应速度及控制精度，但这样会导致超调量的升高。综上所述系统在PID控制下能够迅速响应并实现稳定悬浮。

图4 磁力驱动平台阶跃信号PID控制位移输出

5 小结

对驱动平台的结构及工作原理进行了介绍，建立了系统动力学模型，采用控制量权重分配的方法解决过驱动问题，并且通过分散控制的方法降低了这种多自由度运动控制的复杂程度，同时也保证了系统各个自由度都能达到控制要求。对系统进行了仿真分析，仿真结果表明:在阶跃信号输入下系统能够迅速响应，实现稳定的悬浮，但存在较高的超调量。对于未来的工作则是在保证响应速度及控制精度的同时通过对控制参数的进一步调整来降低系统的超调量。