有机铁磁体自旋输运和载流子特性理论研究

胡贵超 苗圆圆

(山东师范大学物理与电子科学学院，250358，济南 )

1 引 言

近年来，有机自旋电子学吸引了人们越来越多的兴趣[1-3]，它利用电子自旋自由度设计廉价高性能柔性器件.与无机材料相比，有机自旋电子学具有一些独特的优势.首先，有机材料通常由C、H、O、N、S等轻原子构成，原子序数较小，自旋-轨道耦合作用较弱；又因为C原子以12C为主，核自旋为零，超精细相互作用也较弱[2].因此，有机材料内的电子自旋弛豫时间较长[4].其次，有机材料具有“软”特性，与无机材料接触后可发生界面弛豫，降低界面势垒，避免了无机材料器件界面晶格匹配问题[5]，尤其当有机材料与铁磁材料形成稳定的化学接触时，界面势垒的降低不仅有利于电子自旋的注入，还可以导致界面杂化态的产生，对界面自旋极化起到调制的作用，从而引发了“有机自旋界面”的概念[6].最近的实验研究已经表明，利用有机聚合物可以制备常规的自旋电子器件，如磁电阻器件等[7-9].此外，有机材料中强电子-晶格相互作用导致注入的电子以局域态的形式存在，形成各种非线性元激发，如孤子、极化子、双极化子等[10,11]，它们各自具有不同的电荷-自旋关系，自旋输运形式也比无机材料更为丰富.有机材料还有其它一些优势，比如密度较小，种类多样，在工业上易于加工合成等[12-15].随着人们对有机材料研究的深入，甚至发现可以使有机材料在分子水平上表现出磁特性并用于磁存储.因此，利用有机材料构建自旋器件，探究其内部自旋的产生、注入、输运及功能性，具有广阔的应用前景，是有机自旋电子学关注的热点.

目前，以有机材料构成的自旋器件主要分为两类：一类是利用有机半导体作为中间层，两侧为铁磁电极的自旋阀器件[16,17]，主要研究磁性电极与有机半导体之间的自旋注入、输运及磁电阻等现象.另一个是以有机磁体作为中间层的自旋器件，它利用有机磁体自身的磁特性实现自旋功能性，不依赖于两侧电极，易于设计内禀自旋器件.

由于有机磁体结合了有机材料的“软”特性以及磁性材料的磁特性，从而成为有机自旋电子学领域人们关注的焦点.通过在有机材料中掺杂过渡金属离子或施加自旋侧基等方式可以人工合成有机铁磁体(OF)[5,18-21].后一种方法有利于生成纯有机铁磁体，如poly-BIPO是一种典型的具有准一维结构的有机π共轭纯有机铁磁体，它可利用含自旋的侧基间隔取代聚乙炔中的H原子得到，每一个侧基中都含有一个未配对的电子，侧基自旋与主链π电子自旋存在铁磁性耦合[10,11]，基态下侧基呈现铁磁序.目前，实验上人们已经获得了几种较为稳定的自旋侧基[12,18,19]，并测量了多种有机铁磁分子的磁特性，包括高居里温度[18]，磁滞现象和矫顽力[19]等.

在过去的几十年里，人们对有机铁磁体的研究主要集中在孤立分子磁性的合成、测量和表征上.最近，有机自旋电子学和分子自旋电子学的发展，使我们探索有机铁磁体自旋输运性质以及设计有机铁磁器件成为可能.例如对于单分子磁体，实验和理论已经证明可以实现分子开关和负微分电阻等功能性器件[13-16,22-25].Yoo等人[17]通过将有机磁体V[TCNE]x连接到Au电极，研究了有机铁磁器件的磁响应现象.两侧为非对称性电极的有机磁性器件也有研究，并得到了相当的磁电阻效应[26].Wang等人[27,28]对有机铁磁体中的电子输运进行了理论研究，提出了自旋-电荷分离和自旋过滤等现象.

由于π轨道可用于电子传输，因此具有自旋侧基的π共轭有机铁磁体是器件设计的理想材料.如何基于自旋侧基的有机铁磁体设计新型器件，并理解其物理机理，是人们追求的目标.基于扩展的SSH(Su-Schrieffer-Heeger)模型[29]和格林函数方法是研究有机磁体器件输运的有效方法，可有效描述其磁特性和有机软特性，该方面近期有许多研究成果.本文将介绍有机磁体器件的量子输运理论研究，并讨论有机铁磁体中载流子电荷自旋特性与传统有机材料的差异，及其在微观动力学输运中的表现.

2 模型和研究方法

2.1有机铁磁体SSH+Heisenberg模型和格林函数方法

假设有机铁磁分子poly-BIPO两端连接于两个一维半无限大金属电极上，有机分子使用准一维模型描述.整个体系的哈密顿可以写为

H=HOF+HL+HR+Hcoup+HE.

(1)

第一项为有机铁磁体的哈密顿量[10,11],

(2)

HL(R)为左右无限大电极的哈密顿量，用一维紧束缚模型来描述两侧的电极为[30]

(3)

Hcoup为金属与有机铁磁体之间的界面耦合哈密顿量，

(4)

tl(r)mf为左(右)界面电子跃迁积分，N为有机铁磁体中主链碳原子的数目.

最后一项HE是当施加偏压时电场对分子的影响，假设偏压沿分子链主链产生一均匀电场为E=V/[a(N-1)][31,32].则电场产生的哈密顿量为

(5)

e为电子的电荷,a为晶格常数.第一项是π电子的电势，第二项是晶格阳离子的电势.

利用平均场近似处理电子-电子相互作用和自旋关联相互作用，波函数在Wannier表象下展开，通过求解薛定谔方程可以得到电子的本征态,

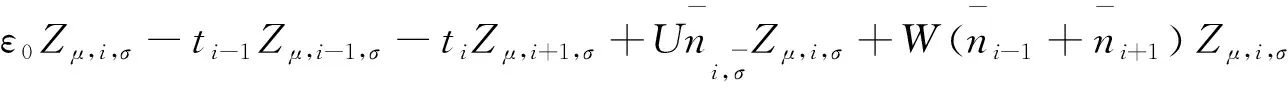
(6)

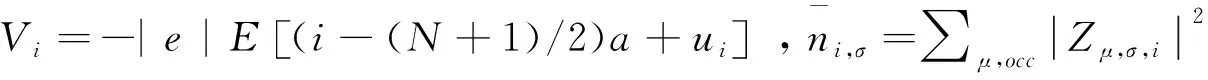
有机铁磁体两端考虑固定边界条件，晶格畸变方程写为

(7)

联立方程(6)和(7)自洽求解可以得到有机铁磁体在偏压下的稳定状态.自旋相关电流可以通过Landauer-Büttiker计算得到[33]

(8)

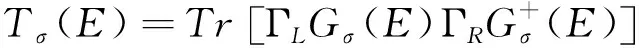
2.2有机铁磁体SSH+Anderson模型以上模型将侧基自旋看作一局域自旋，未考虑侧基未配对电子与主链之间的跃迁.考虑到侧基未配对电子与主链之间的跃迁，可用Anderson模型描述一维有机磁体，哈密顿量为

H=H0+H1.

(9)

H0是主链扩展的SSH哈密顿量，

(10)

H1描述侧基哈密顿量以及侧基与主链之间的电子跃迁项，

(11)

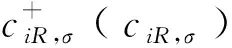
利用平均场近似处理电子-电子相互作用，通过求解整个体系的电子本征方程，可求得本征值和波函数,

(12)

周期性边界条件下的晶格平衡方程为

(13)

方程(12)和(13)可联立自洽求解.

2.3有机铁磁体动力学模型动力学过程中电子部分的哈密顿量写为

(14)

晶格部分的哈密顿量包括晶格动能和晶格弹性能,

(15)

动力学计算过程中，电子态的演化可以通过求解含时薛定谔方程得到

(16)

晶格坐标的演化可以通过求解经典的牛顿方程得到

(17)

方程(16)、(17)可联立自洽求解.

3 有机铁磁器件自旋极化输运

3.1金属/有机铁磁体/金属器件中的自旋过滤自旋过滤是指传输电流只包含一种自旋的载流子，自旋极化率为100%.在传统自旋电子学研究中，基于三明治结构使用磁性夹层是一种有效的方法，如Ag/EuSe/Al和Ag/EuS/Al[35,36]结构形式的器件.在这些器件中，为获得强自旋极化的电流，通常需要强磁场来进行操控.我们的一项研究工作表明，利用有机铁磁体作为中间夹层，可实现内禀的有机自旋过滤器[37].我们将有机铁磁分子夹在两个全同的非磁电极中间，利用前面提到的SSH+Heisenberg模型结合格林函数方法，理论计算了器件的自旋极化输运.这里定义电流的自旋极化为P=(I↑-I↓)/(I↑+I↓).研究发现，在低偏压下通过有机铁磁分子器件的电流是自旋极化的.如图2所示，电流的自旋极化随外加偏压呈现振荡的行为.当偏压增加到0.5 V时，器件开始导通，此时电流的自旋极化率几乎达到100%，可实现自旋过滤的功能.而当偏压继续增大到1.2 V时，自旋极化率又由100%降到接近零.当偏压增加到1.8 V时，电流自旋极化率出现第二个峰值，然而,此时的电流仅仅部分自旋极化，自旋极化率大约为40%.随着偏压的继续增大，电流自旋极化率将会出现多个峰值，但振幅将会越来越小.

图1 有机铁磁体器件结构示意图

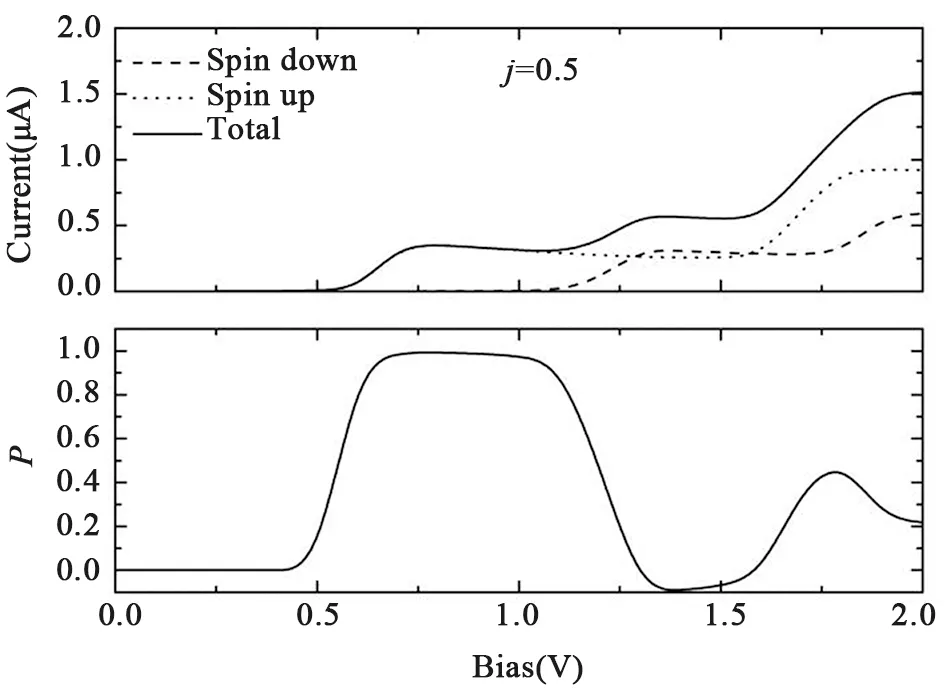
图2 有机铁磁体器件I-V特征曲线及电流自旋极化

为理解自旋过滤效应，计算了偏压为0.8 V时的电子态密度，如图3所示.由于侧基自旋关联的存在，主链π电子能态发生自旋劈裂.同时，电子-晶格耦合使得自旋向上的最高占据分子轨道(HOMO)和自旋向下的最低未占据分子轨道(LUMO)之间出现大约1.0 eV的能隙.在低偏压下，只有自旋向上的电子态进入偏压窗口并对电流有贡献.因此，电流几乎完全自旋极化.当偏压增加时，自旋向上和自旋向下的电子态交替进入偏压窗口，导致自旋极化随偏压振荡.这表明有机铁磁电子-晶格耦合和侧基自旋关联作用在自旋过滤中起重要作用.

图3 有机铁磁体分子在费米能级附近的态密度(DOS)

3.2铁磁金属/有机铁磁体/铁磁金属器件中的多态磁电阻传统有机自旋阀器件两端采用铁磁金属作为电极，中间为非磁分子，通过磁场调控两端电极磁矩平行和反平行，可实现高阻态和低阻态输运，即磁电阻现象.如果中间分子为有机磁体，体系三组分之间的磁矩排列将更为复杂，有八种方式.考虑到不同自旋对电流贡献的简并，体系有四种不同的磁矩组合.通过磁场控制这些状态，有可能实现多态磁电阻现象.基于此理论设想，研究了Co/ poly-BIPO/Co器件中的磁电阻现象[38]如图4所示.这四种构型被标记为C1 (↑↑↑)、C2(↓↑↓)、C3(↑↑↓)和C4(↓↑↑).图5计算了四种构型下的I-V特征曲线图.研究发现阈值电压和电流值依赖于磁序结构，C1构型首先导通，阈值电压约为0.3 V.当偏压超过0.8 V时，最大电流约为2.7 μA.C2和C4构型下的阈值电压较大，电流较小，而C3构型下的电流在计算偏压区域内被强烈抑制.

图4 态密度(a)Co；(b)有机铁磁体；(c)Co/有机铁磁/Co器件的磁化取向排列

图5 Co/有机铁磁体/Co器件中四种自旋构型下的I-V曲线

我们进一步定义偏压下的多态磁电阻为MRi(V)=[RCi(V)-RC1(V)]/RCi(V).表1总结了每种构型下的阈值电压、最大电流和1.0 V时的磁电阻.显然，随着磁化方向的改变，可实现四个明显不同的磁电阻值.在1.0 V偏压下，最大磁电阻可达98%.

表1 不同构型下的阈值电压(Vth)、最大电流(Imax)和磁阻(MR)

通过计算四种构型下的透射谱我们可以进一步理解该现象.如图6所示，对于C1和C4构型，自旋向下LUMO的电子透射峰位于偏压窗内，贡献电流.然而对于C2和C3，在偏压窗中没有透射峰值，因此电流较小.这是因为对于目前计算的结构，费米能级附近最靠近的分子轨道是自旋向下的，如图4b所示.因此，对于C1和C4构型来说，只有自旋向下的电子才能通过.

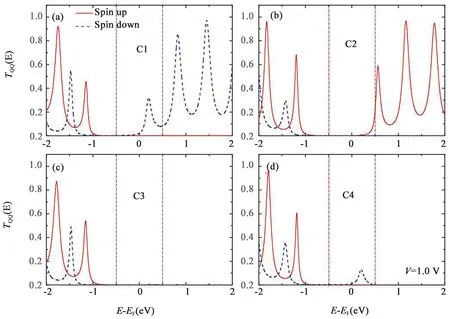
图6 四种构型下费米能级附近的自旋相关透射谱

3.3铁磁金属/有机铁磁体/金属器件中的隧穿磁电阻相比于传统分子自旋阀，有机磁体由于自身的磁特性，即使采用单极铁磁电极，也可实现磁电阻现象.我们将有机铁磁体同磁性电极Co和非磁电极Au相连接，计算了器件中的自旋相关输运[39].结果表明，通过控制铁磁金属和中心有机铁磁体之间的相对磁化方向，即平行或反平行排列，可以获得高达3 230%的隧穿磁电阻(TMR).图7展示了磁矩平行(P)和反平行(AP)排列时体系的I-V曲线和磁电阻.显然，P构型具有更小的阈值电压和更大的电流值.如在正偏压下，P构型的阈值电压约为0.5 V，电流在1.0 V时达到2.7 μA.AP构型的阈值电压为0.6 V，而1.0 V时的电流仅为1.4 μA.负偏压下情况类似.在图7(b)中，TMR随偏压曲线表明，在P构型的阈值电压附近出现两个极值峰，一个位于0.54 V，幅度约为887%，另一个位于-0.64 V，数值为3 230%.在1.0 V时，TMR最小值也可达到约100%.

以上TMR机制可通过能带隧穿示意图理解.如图8所示，左侧Co电极能带自旋劈裂，多子为自旋向上的电子，能带满占据，少子为自旋向下的电子，能带部分占据.右侧Au电极能带自旋简并而且都是半满占据.在现有参数下，中心有机铁磁体中自旋向下的LUMO靠近费米能级.因此，在低偏压下，只有自旋向下的电子能够通过分子轨道隧穿.当施加0.6 V的正偏压，Co电极能带抬升，Au电极能带降低.在P构型中，Co电极中自旋向下的电子通过分子自旋向下的LUMO轨道进入Au电极自旋向下的能带.在AP构型中，传输则是由左侧自旋向下的多子带到右边自旋向下的半满带中的电子隧穿贡献的.P和AP两种情况下Co电极的隧穿态能带不同，P构型与能带中间态有关，而AP构型与边缘态有关.因此，P构型的传输远大于AP构型，从而导致较大的TMR.同样的，对于反向偏压，在P构型中，隧穿发生在电极的两个半满自旋带中间.然而，在AP构型中，由于Co电极中的自旋向下的能带已经被完全填充，因此，自旋向下的电子从Au到Co的隧穿被禁止，导致AP构型中的透射被完全抑制，从而产生极高的TMR.

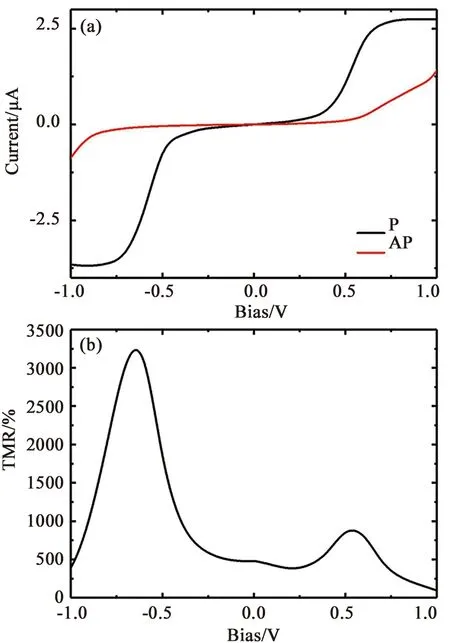
图7(a)电流-电压曲线；(b)偏压下隧穿磁电阻

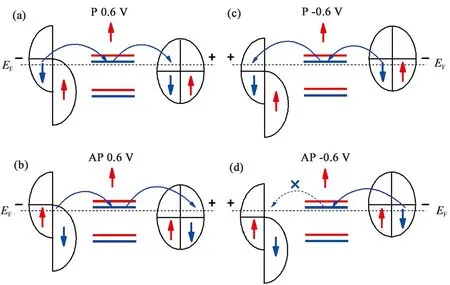
图8 磁性电极/有机铁磁体/非磁电极异质结的能带隧穿示意图

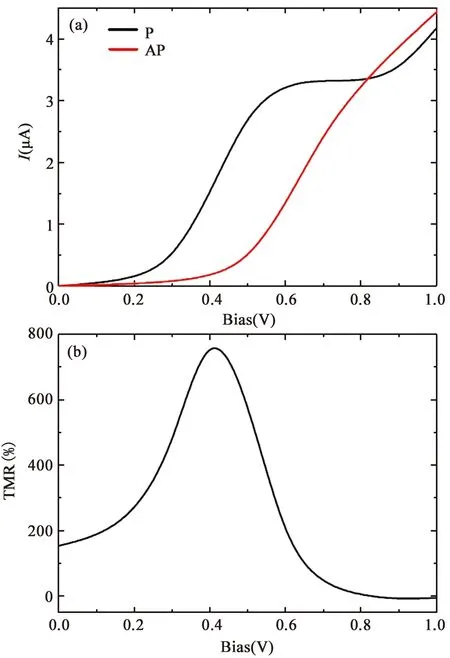
图9(a)P和AP构型下的I-V特征曲线图(b)偏压下器件的隧穿磁电阻

3.4金属/有机铁磁共聚物/金属器件中的轨道杂化和磁电阻我们进一步设计了一种基于有机铁磁的内禀的分子自旋阀.中心磁性分子由两种具有不同矫顽场的有机磁体OF1和OF2组成，两电极为非磁性金属电极.假定两部分有机铁磁之间的自旋取向可以是平行(P)或反平行(AP).我们从理论上研究了此类有机铁磁共聚物在不同自旋构型下的轨道杂化和自旋相关输运[40].结果表明体系的杂化轨道对两部分的自旋构型非常敏感.通过计算不同自旋结构下的输运性质，发现体系可实现较大的TMR(～757%).如图9所示，在P构型下，电流在0.25 V后开始快速增加，但对于AP构型，在0.5 V后电流出现急剧增加.两种情况下的最大电流都超过4.0 μA.图9(b)给出了与偏压相关的TMR效应.在低偏压下观察到正的TMR，并且随偏压快速增加.在0.4 V时TMR最大值达到757%，这比大多数传统基于铁磁电极的分子自旋阀中的TMR大得多.当偏压超过0.4 V时，TMR下降，甚至在0.8 V后变为负值.

该体系中的TMR物理机制可通过轨道分析进行理解.对于磁性共聚物，其电导能力取决于两组分之间的轨道杂化.轨道杂化取决于两个片段的自旋构型.此处我们聚焦于自旋向上的HOMO来理解杂化对自旋构型的依赖性.图10(a)和(b)显示了不同自旋构型下轨道杂化前后的分子能级.在P构型下，孤立的OF1和OF2的能级是自旋分裂的，自旋向上的能级抬升，自旋向下的能级降低.磁性共聚物自旋向上的HOMO主要是由两组分中自旋向上的HOMO杂化贡献.当自旋组态变为AP时，我们假设自旋耦合参数较小的孤立OF2的自旋劈裂发生反转.此时，孤立分子中两个自旋向上的HOMO之间的能量差相比P时增大.这种自旋构型导致的能量失配改变了杂化，导致杂化之后自旋向上的HOMO远离费米能级，降低了体系的电导.

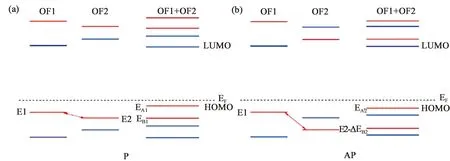
图10 P和 AP构型下OF1和OF2之间的轨道杂化示意图.箭头表示轨道的杂化作用.红(蓝)线表示自旋向上(向下)的能级

3.5非对称磁性共聚物器件中的自旋整流以上主要介绍了有机磁体器件中的磁电阻现象.接下来，我们介绍非对称有机铁磁器件中的自旋整流现象.电荷流整流是指器件单方向导通，即偏压反向时I-V曲线不对称，这要求器件的结构具有空间非对称性.在过去的几十年中，人们设计了多种非对称结构来研究分子整流，如分子/电极界面不对称或中心分子的不对称[32,41-45].自旋流整流是偏压反转时自旋流不对称，它比电荷流整流更复杂.通常我们定义电荷流为Ic=I↑+I↓，定义自旋流为IS=(ћ/2e)(I↑-I↓).因此，自旋流包含两方面特征：流的幅度和自旋极化.因此，偏压反转时自旋流的不对称有两种可能：第一种是流幅度不对称，而自旋极化保持不变，这类似于电荷整流.我们称这种效应为平行自旋流整流.第二种是偏压反转时，自旋极化发生反转，我们称之为反平行自旋流整流.自旋整流的实现需要器件结构在自旋自由度具有非对称性.我们提出一种有机自旋二极管模型[46]，该模型中间分子为磁性/非磁共聚物，两端为非磁电极.中心磁性共聚物由左侧有机铁磁体分子和右侧非磁性分子组成，例如poly-BIPO和聚乙炔.结合自旋相关的Landauer-Büttiker公式计算了通过器件的电流及其自旋极化率.研究发现，反转外加偏压，器件可同时或分别出现电荷流整流和自旋流整流.在不同参数下，可得到以上两种形式的自旋整流.

如图11给出了初始费米面位于分子能隙中央时的电流和自旋流结果.发现电流对称，不存在整流，而自旋流随偏压反向时自旋极化取向出现反转，即反平行自旋流整流.其机制可通过不同偏压下费米能级附近自旋相关的电子透射谱来理解.图12中给出了0 V和±1.0 V下的自旋相关透射谱.在0 V时，自旋向上的LUMO透射峰与自旋向下的HOMO透射峰关于费米面左右对称.施加1.0 V的正向偏压，HOMO自旋向下的透射峰向费米面靠近，并进入偏压窗，从而贡献了自旋向下的极化电流.反之，当施加-1.0 V的偏压时，偏压窗中只有LUMO自旋向上的峰.由于HOMO和LUMO在正负偏压下的演化是对称的，因此，尽管出现自旋流整流，系统的电荷流仍然是对称的，没有电荷流整流现象.

图11 不对称有机铁磁体中与偏压相关的电荷流和自旋流(N=20，EF=0)

图12 不同偏压下费米能级附近的自旋透射谱(N=20，EF=0)

电极费米能级相对于分子能隙的位置对于整流行为很重要.通过调节其相对位置可使电荷通道不再关于费米面对称，从而导致电荷流和自旋流同时整流，如图13所示.在反向偏压下，电流(自旋流)绝对值小于0.1.而在正向偏压下，当V > +0.6 V时电荷流和自旋流迅速提升.因此，体系同时出现电荷流整流和自旋流整流.此时自旋流正负偏压下自旋极化相同，流的振幅不同，出现平行自旋流整流的现象.根据图14所示的与偏压相关的透射谱，可以理解其潜在的机理.可以看到，正负偏压下都是自旋向上的LUMO轨道导通.然而，与负偏压相比，在正偏压下的透射率显著增强，因此在正偏压下具有更大的自旋极化电流.

图13 磁性/非磁有机分子器件中的电荷流和自旋流(N=32，EF=0.3)

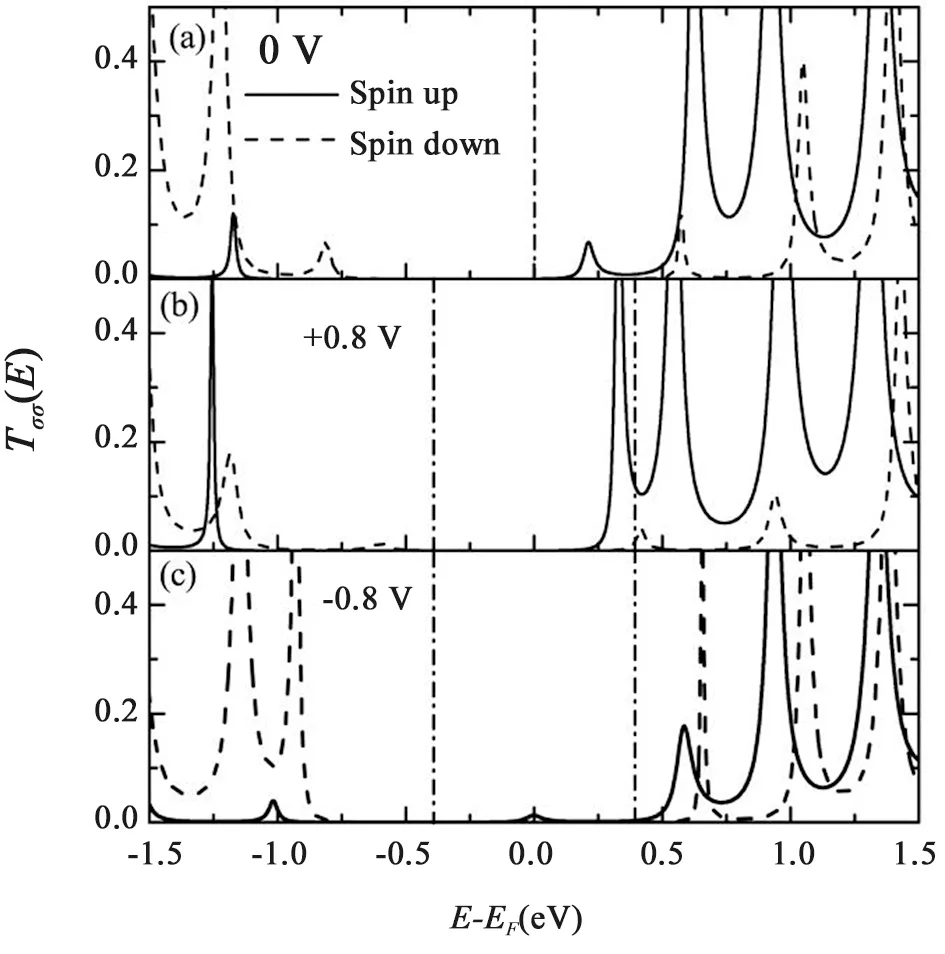
图14 不同偏压下费米能级附近的自旋透射谱(N=32，EF=0.3)

4 有机铁磁体中的载流子特性及动力学输运

4.1有机铁磁体中的极化子除了有机铁磁器件的量子输运特性，我们进一步介绍了有机铁磁聚合物中的非线性载流子磁电特性及相关动力学研究.对于有机铁磁体，由于磁性自由基的存在，使有机铁磁中的载流子出现与传统有机聚合物不同的性质.我们采用Anderson模型详细的研究了poly-BIPO分子基态及掺杂一个电子后的极化子态的电荷自旋特性[47].结果如图15所示，该有机铁磁体在基态下呈现铁磁性，掺杂一个电子后形成带有分数电荷和自旋的极化子.极化子电荷自旋畸变同时出现在主链和侧基上，且极化子的电荷和自旋存在空间分布不一致现象.这种电荷-自旋不一致性可从背景电子费米海的影响来进行理解，即去除掺杂电子外的其它电子的影响.如图16所示，与中性态相比，当出现极化子时，费米海电子在主链与侧基的电荷与自旋密度分布都发生了畸变.这种畸变主要是由极化子晶格畸变的扰动以及附加电子的库仑斥力所引起.费米海中电荷和自旋密度的畸变空间分布不同，从而导致极化子的自旋-电荷分布产生差异.引起极化子电荷-自旋不一致的另一个原因是存在极化子的情况下，费米海电子在主链和侧基之间存在电荷和自旋转移，且大小不一致.

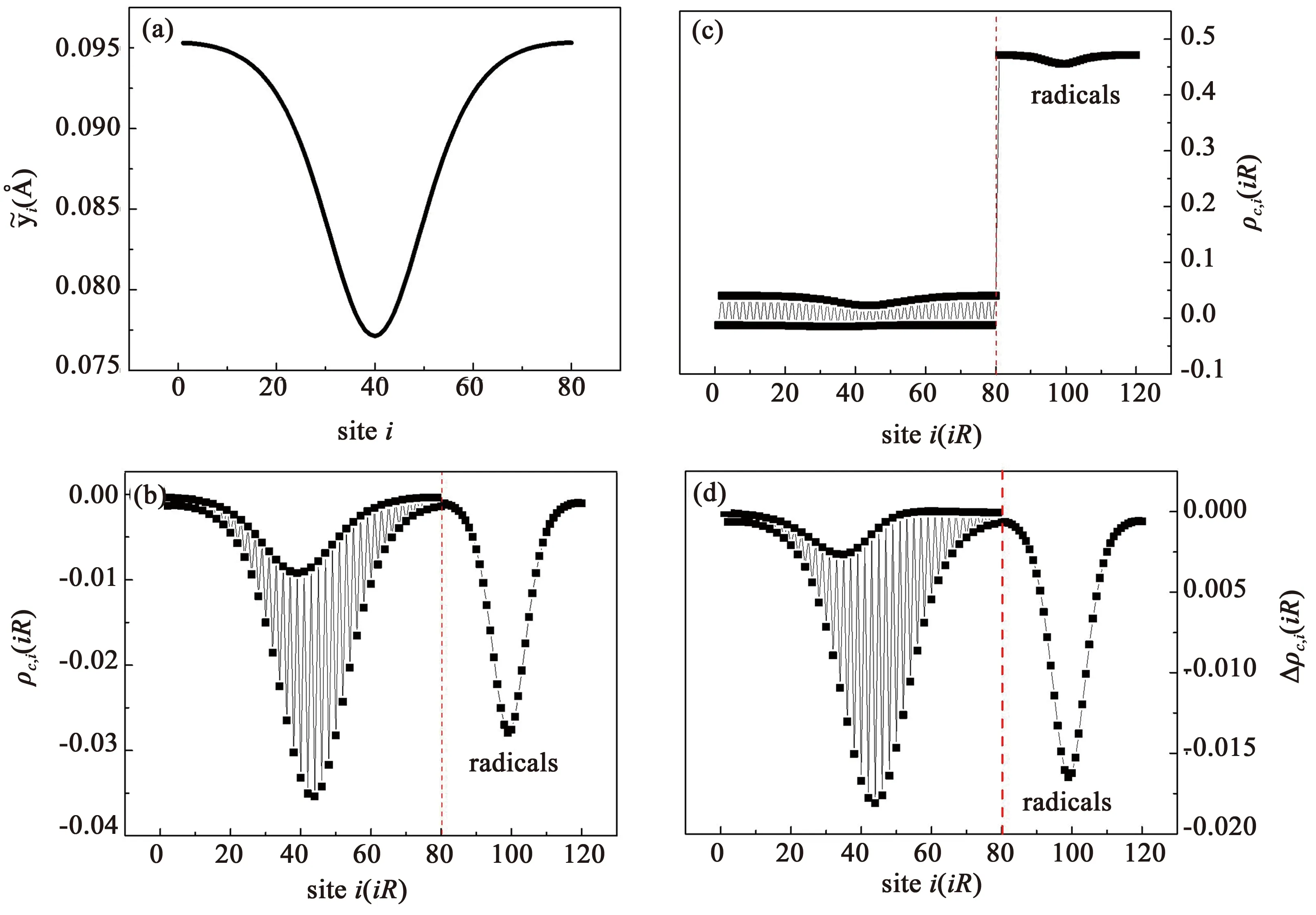
图15 有机铁磁体的极化子态：(a) 晶格结构；(b) 电荷密度；(c) 自旋密度；(d) 净自旋密度

图16 极化子态下费米海电子的电荷和自旋密度分布

4.2金属/有机铁磁体异质结的基态性质对于有机铁磁器件，有机磁体同金属电极耦合后界面微观性质对理解器件物理特性比较重要.我们对金属/有机铁磁体系的基态性质进行了研究[48].金属材料分别考虑非磁性金属和铁磁金属.研究发现，对于非磁性金属，通过调节金属与分子相对化学势，金属与有机铁磁体之间可发生电荷转移.如图17所示，转移过程分为两个步骤，首先形成类孤子界面态，然后随着注入电子的增加，逐渐产生极化子态.之后随注入的电子继续增加，形成的极化子态也增多.

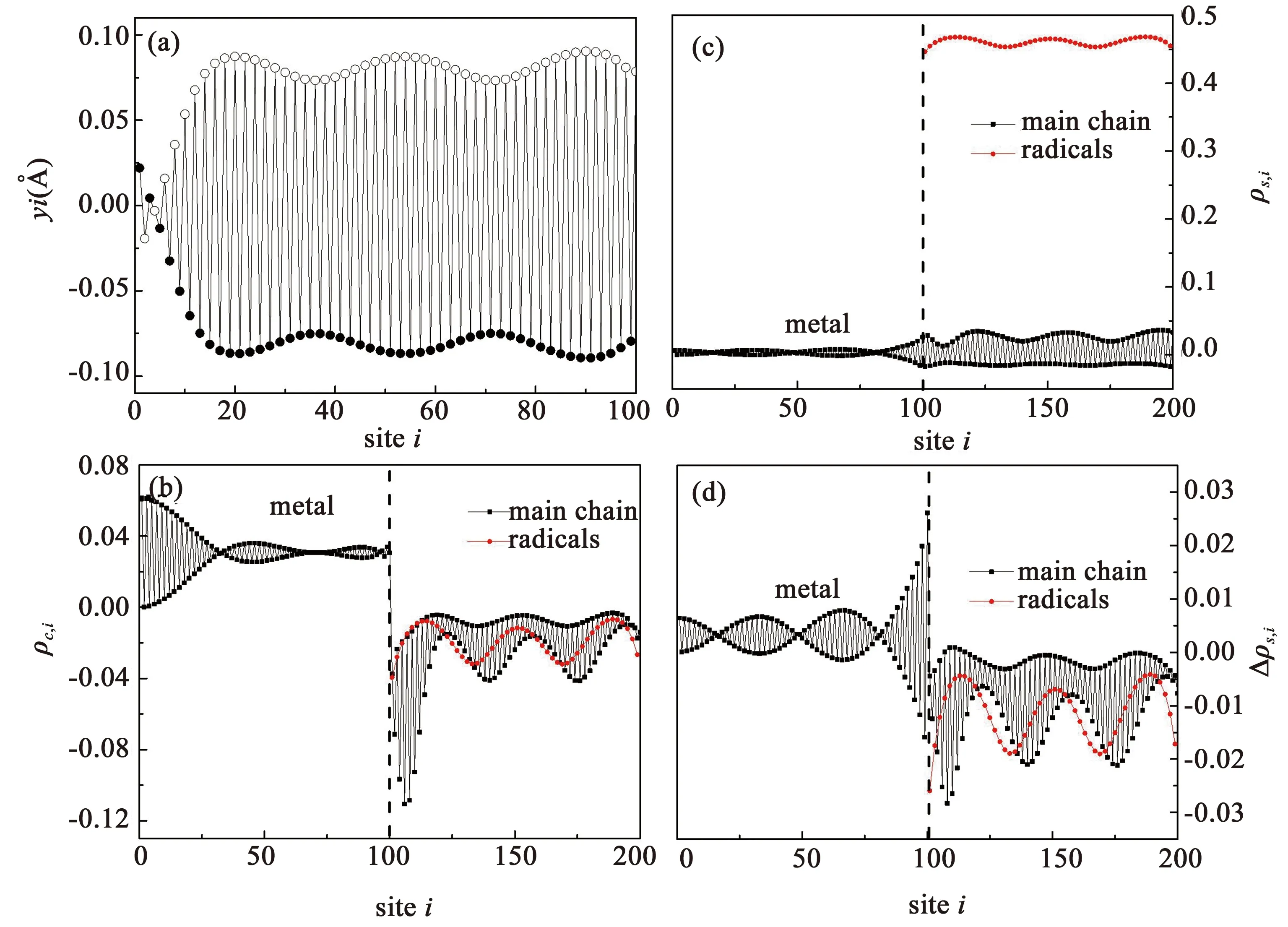
图17 普通金属/有机铁磁体系的基态性质

在我们的算法中，允许电子自旋反转保持最低占据，因此体系的磁矩可不守恒.如图18所示，随着金属在位能ε的增加，当达到某一值时，金属中一个自旋向上的电子通过自旋反转注入到有机铁磁体中，体系的总自旋变化为-1 .由于有机磁体中最低未占据能级是自旋向下的，因此金属与有机磁体之间的电子转移会使有机磁体中总自旋减少，进而削弱铁磁性.在自旋向下的能带完全被占据时，分子的铁磁性将被最终消除.

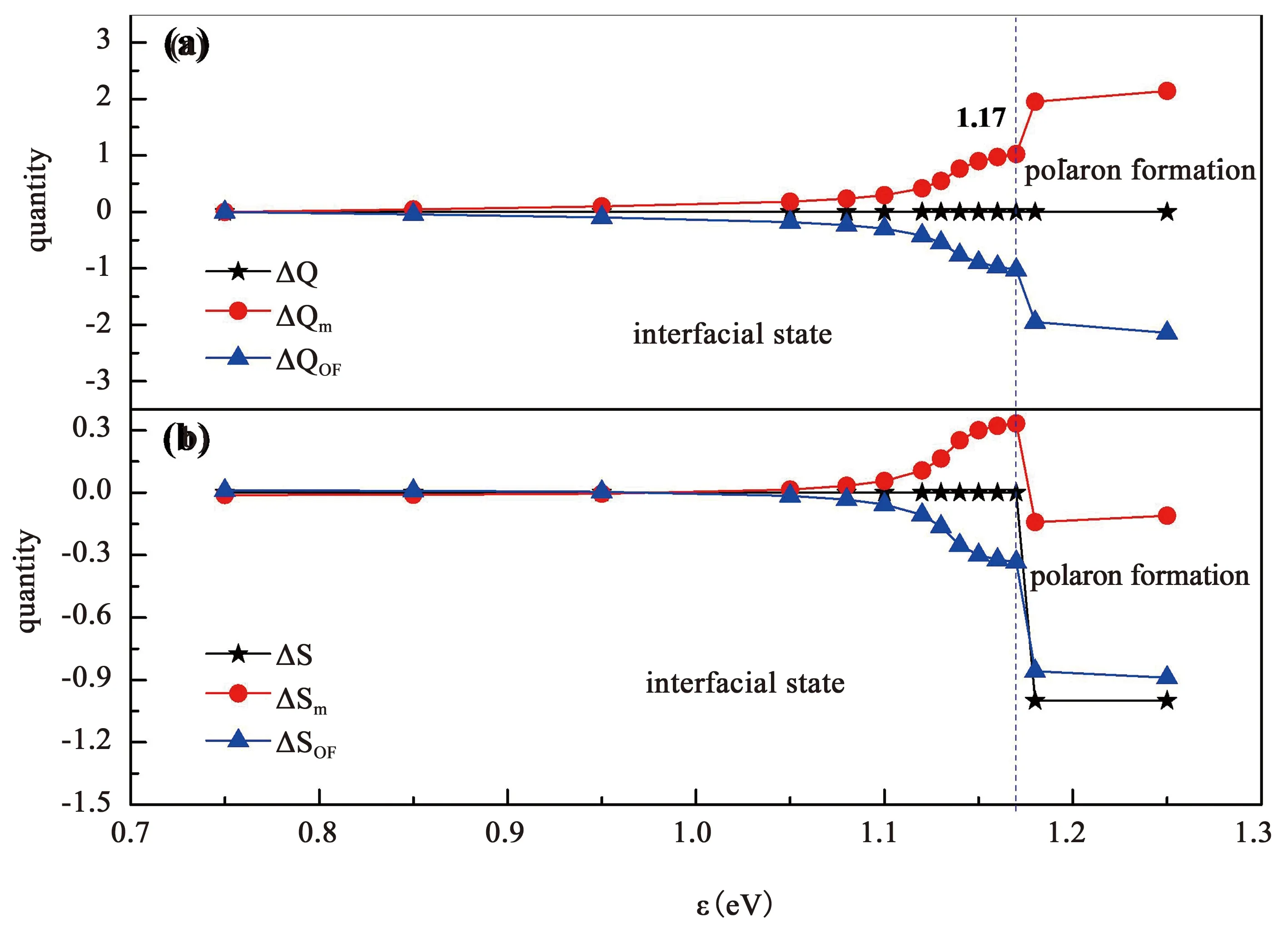
图18 有机铁磁体、金属以及整个体系中的净电荷与相应净自旋的变化

此外，在铁磁金属的情况下，进一步讨论了金属与有机磁体磁化取向匹配对自旋转移的影响.如图19所示，当两部分磁化方向平行时，注入势垒最小，自旋反转发生在极化子形成之后.反平行情况下，注入势垒较大，自旋反转伴随电子注入同时出现.此外，还发现电子注入可能引起有机铁磁体磁性的消退.

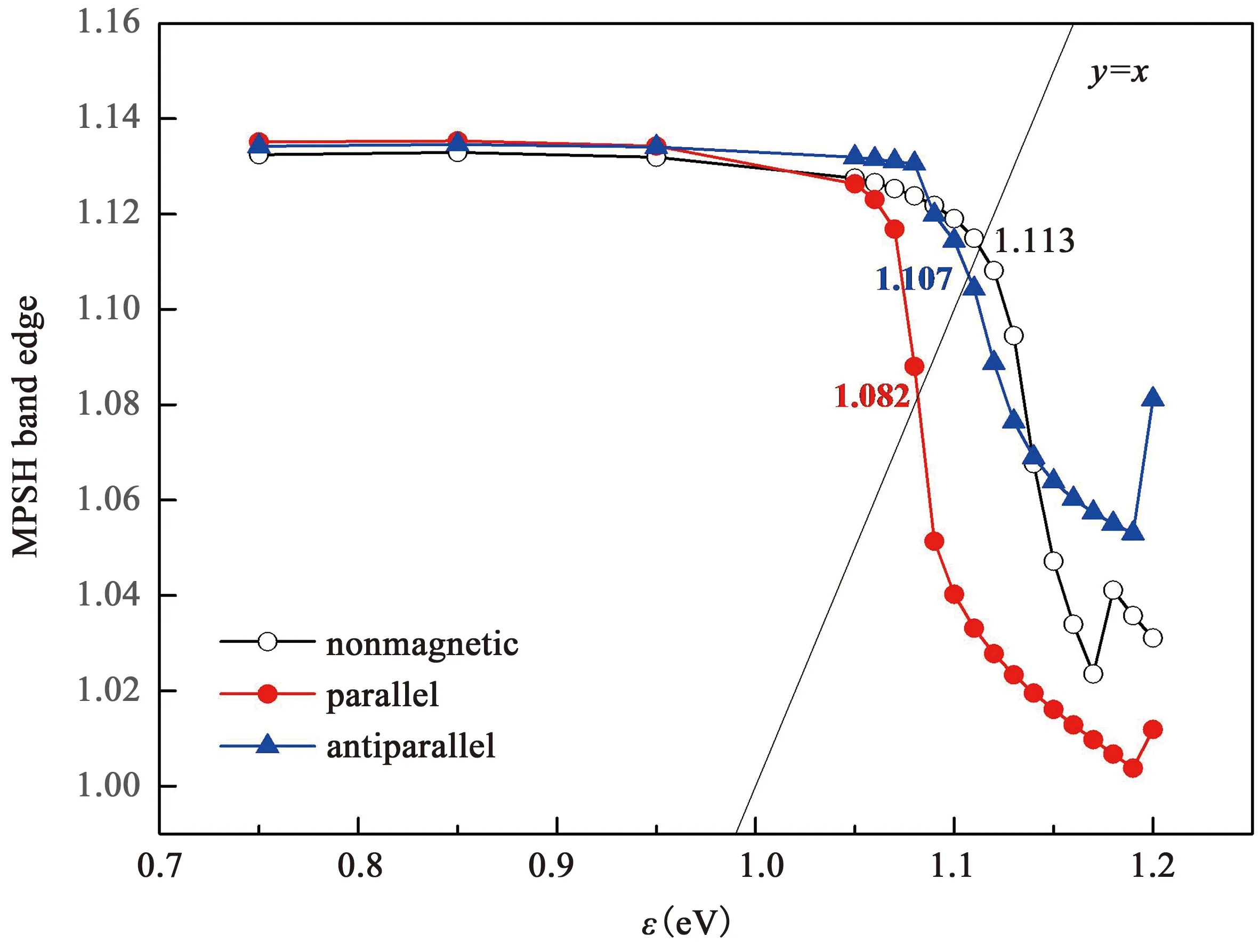
图19 不同金属情况下，最低未占据MPSH能级随ε的变化

4.3弱场下有机铁磁体中的极化子动力学最后我们用非绝热动力学方法研究了弱电场下有机铁磁体中的极化子动力学[49].由于自旋侧基的存在，发现该过程存在两种不同于普通聚合物的新现象.如图20所示，可以看到极化子在不同外加电场方向下运动速度是不对称的.另外，极化子运动在电场下存在一“间歇反弹”现象.这两种现象的产生可以从不同方向电场作用下的极化子电荷密度及其晶格畸变来解释.在没有施加电场时，由于电荷密度相对于极化子中心的不对称分布，极化子存在本征偶极矩.在施加电场后，极化子的电荷密度在电场下重新分布使得偶极矩在电场反转时不对称.如图21(a)所示，当施加一个向左的电场时，更多的电荷分布在极化子的右侧.所以，施加向左的电场比施加向右的电场产生的偶极矩要更大一点.由于电子-晶格耦合，这种不对称的电荷分布进一步影响晶格畸变.如图21(b)所示，在向左的电场下出现较深的晶格畸变，对应于更大的极化子有效质量，在相同电场大小下运动速度更慢.

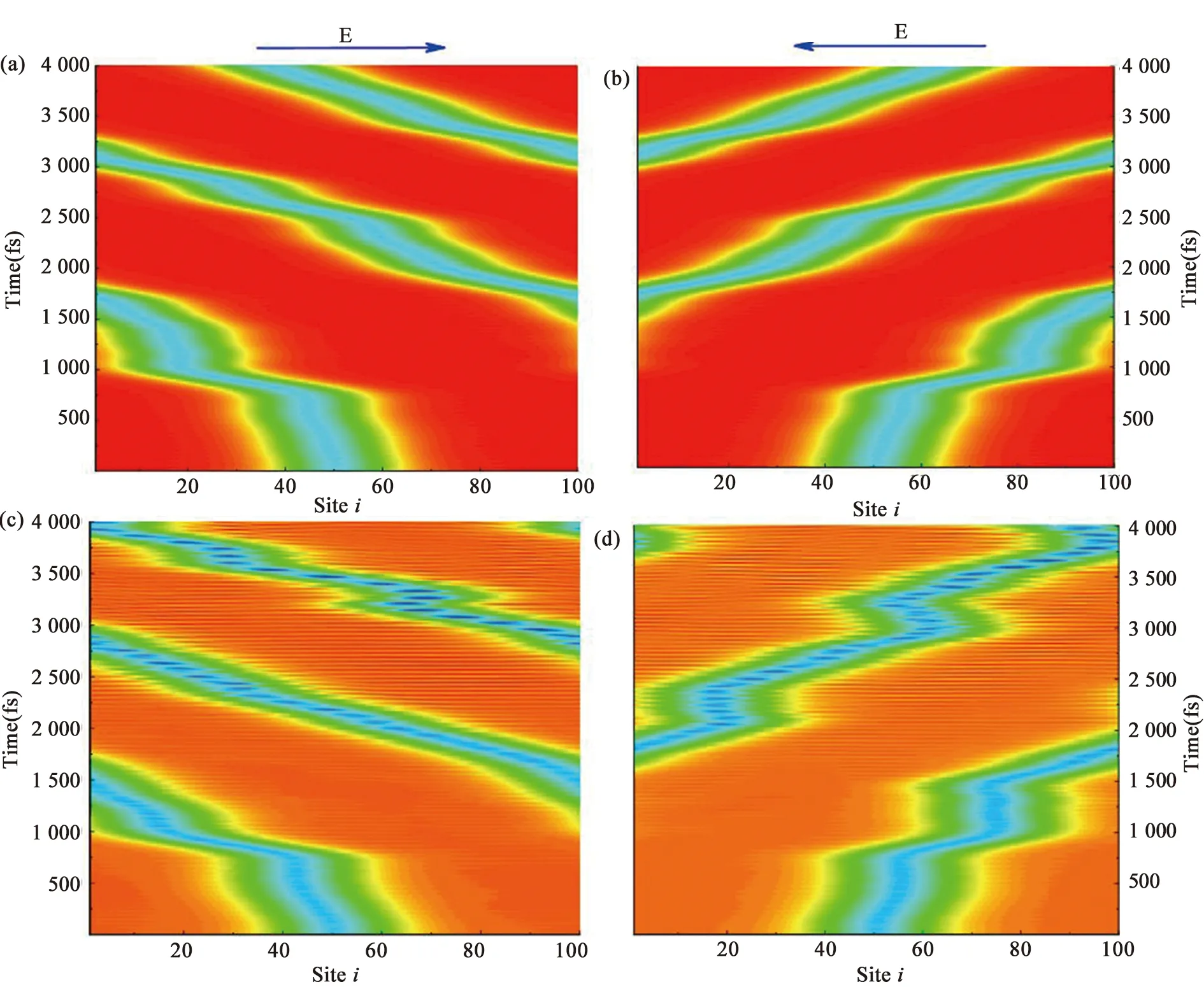
图20 不同电场方向下晶格畸变随时间的演变：(a)、(b)为非磁有机物，(c)、(d)为有机铁磁体

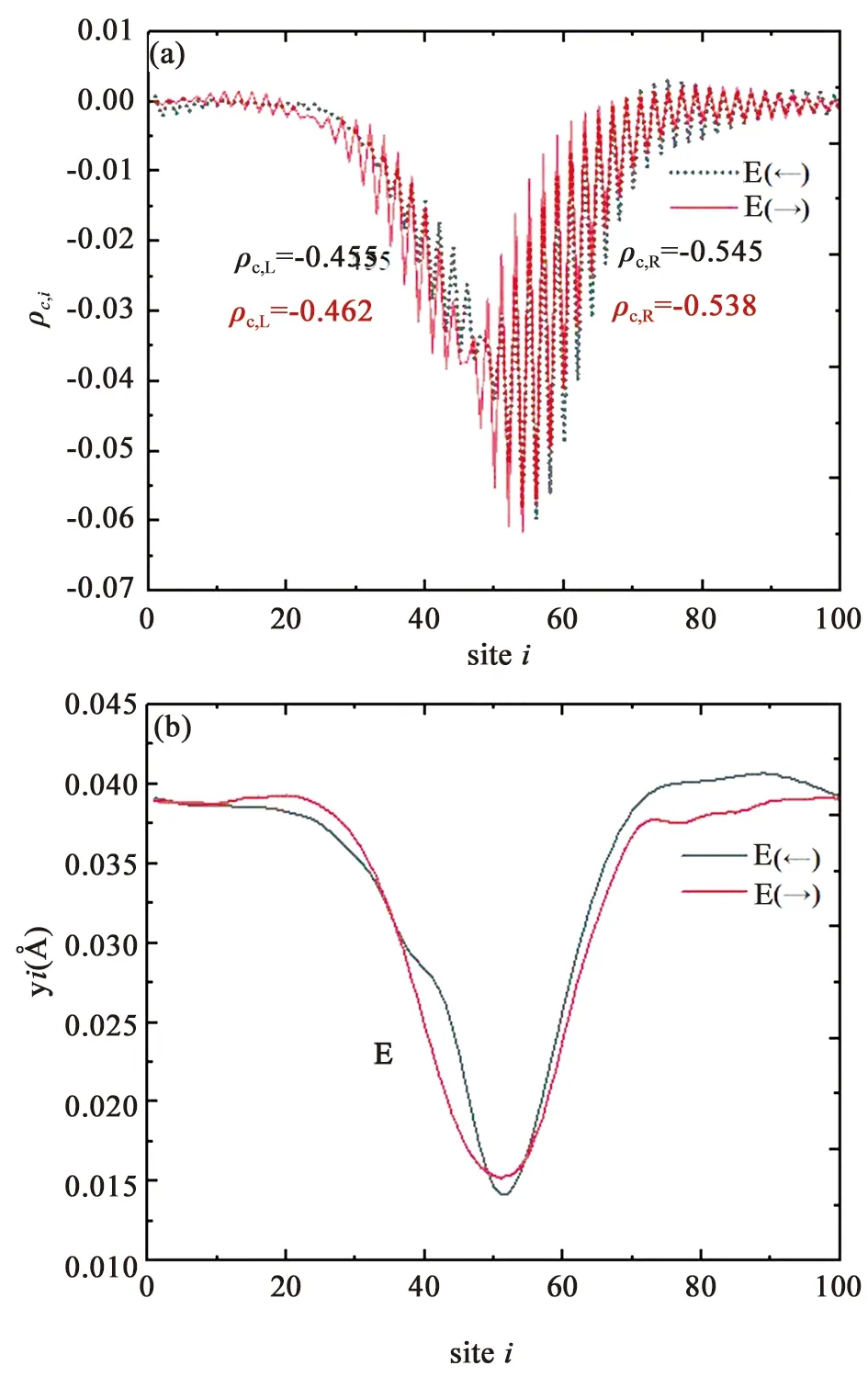
图21 不同电场方向下极化子的电荷密度和晶格畸变

对于极化子的“间歇反弹”现象，我们给出了极化子在这一过程中晶格畸变和电荷密度的不对称性变化来获得更多的细节理解.如图22(a)所示，我们计算了四个不同时刻处的晶格畸变，可以看到，在t1和t2之间的第一个时间间隔内，极化子从第40个格点处移动到第60格点处.然而，在t3时刻极化子反弹回第50个格点处.在电场的驱动下，极化子在t4时刻又再次前进到第70个格点处.从t1到t4这整个过程大约需要780 fs.这种现象表明，外电场下有机铁磁器件中可能会出现短暂的“负电流”.图22(b)给出了四个时刻极化子中心左右两部分电荷差.发现在t2和t3时刻，体系的电荷不对称性大大减弱，这意味着电荷的电势增加，此时极化子动能损失.在t4时刻电荷不对称性大大增强，电势能降低，电势能转化为动能，极化子开始再次加速前进.

图22(a)极化子在四个不同时刻的晶格畸变，电场向左；(b)四个不同时刻左右电荷相对于极化子中心的差值

5 结 语

在本文中，我们回顾了有机铁磁器件中的自旋输运研究，介绍了多种磁电阻器件设计模型，并阐明了有机铁磁聚合物中的微观载流子特性及弱场下的动力学过程，介绍了有机铁磁和金属耦合后的界面基态特性.在此过程中，揭示了有机铁磁体中的内在相互作用，即电子-晶格相互作用和π电子与侧基之间的自旋耦合在其中的作用.内容涉及自旋过滤、磁电阻和自旋整流等物理现象.以上研究有助于人们理解有机铁磁器件自旋输运特性，对未来设计新型有机铁磁器件具有重要的理论指导作用.