浅论幸福的概念和幸福量值的理论计算公式
2021-10-11陈实
陈实
(河南省南阳市中光学集团,河南 南阳 473000)
引言:要想建立统一的幸福的概念,就要使得这个幸福的概念要具有普遍性,适合每一个人。确定了幸福的概念后,如果能够找出幸福的数学表达式,就可以计算出幸福量值来。这样就可以通过比较个人生活在各个不同时间阶段中所获得的幸福值,评价出自己在获得这些幸福过程中的行为的是与非、优与劣来。也可以通过这种对比的方式比较出个人获得幸福的方式的是与非、优与劣来。
幸福的概念和幸福量值的表达式建立之后,必将对人们进一步研究幸福具有极大的推动作用。
一、探索幸福
在现实生活中,我们每一个人都曾经感觉到了幸福的存在。这些幸福的存在似乎与德行无关、与良知无关、与知识无关、与能力无关、与贫富无关、与地位无关、与权势无关、与身份无关、与荣誉无关、与感情无关、与爱情无关、与婚姻无关、与家庭无关、与相貌无关、与年龄无关、与性别无关、与年代无关、与地理位置无关、与国界无关、与种族无关、与民族无关、与信仰无关、甚至与身体是否康健无关、与社会无关。因为不管是什么人,在他们每一个人的一生中都可以找到幸福和不幸的存在;不管一个人是什么样的,他都会面对自己的幸福和不幸的存在。(参见下面的两个举例证明。)所以说,幸福的存在具备了普遍的意义,幸福的概念也必须要具备普遍的意义,否则就不能成立,不能被普遍接受。普遍性是幸福概念的特性之一。
举例证明1:因为每个人都有饭饱满足的时候;而且饭饱满足的人群中可以找到任何身份的人。人在饭饱满足阶段是幸福的。所以,幸福的存在(幸福的概念)与人的身份无关。
举例证明2:因为每个人都要生病痛苦;而且生病痛苦的人群中可以找到任何身份的人。人在生病痛苦阶段是不幸的。所以,不幸的存在(不幸的概念)与人的身份无关。
既然幸福的概念具有普遍性,涵盖了每一个人,或每一种人。可是,每一个人或每一种人,他们所获得幸福的方式又是那么的不同:有些人从德行的累积中获得;有些人从良知的行为中获得;有些人从求知中获得;有些人从探索中获得;有些人从事业中获得;有些人从富贵中获得;有些人从地位中获得;有些人借助身份获得;有些人从权势中获得;有些人从付出中获得;有些人从荣誉中获得;有些人从友谊中获得;有些人从爱情中获得;有些人从婚姻家庭中获得;有些人因为貌美而获得;有些人从健康中获得;有些人从竞争中获得;有些人以其他方式获得。用这些所有的完全不同的方式都可以获得幸福,那么就可以推出幸福的概念一定是抽象的,是可以用数学的表达式来表达的。幸福仅仅是这些不同方式所要获取的目标,而不是这些不同方式的本身。所以说幸福的概念一定具有抽象性,而这抽象性也是幸福概念的特性之一。
幸福的概念具有抽象性,可以用数学表达式来表达,也就是说,幸福是可以计算出幸福量值的,也是可以比较大小的。
幸福的概念具有普遍性和抽象性。但是幸福究竟应该是一个什么样的概念呢?幸福量值的大小是如何计算的呢?
二、寻找幸福
由于幸福概念具有普遍性,所以由此作为切入点,以便能够揭开幸福概念神秘的面纱,让她清晰地展现在盼望已久的人们的面前。
人们普遍体会到幸福是人们自身可以感觉到的东西,也就是说幸福与人的感觉有关。感觉这个概念就具有普遍性,涵盖了每一个人或每一种人。有许多人把这种感觉本身当作幸福,这样做的结果总是让人把幸福解释不清楚。仅有感觉这一个要素还是构不成幸福的,只能把这种感觉称作为幸福感。
人们之间还有什么共同点呢?有,那就是生命!每一个人或每一种人都有生命,生命具有普遍性。离开了生命,谁还会再有幸福呢?我们说幸福,也一定是针对人的某一个生命阶段而言的,所以,生命也是幸福组成的一个要素。
有了感觉和生命,是否就可以构成幸福了呢?如果可以,它们又是如何构成幸福的呢?答案要从幸福的抽象性中寻找。因为幸福具有抽象性,所以幸福就可以用数学表达式来表示。
人的感觉与生命关联,对应着每一个生命时刻都有感觉的存在,即感觉是生命的函数。让我们看看,当感觉函数对生命累积后会得到什么?
令感觉函数记为G=G(T),生命记为T,则有数学表达式为:
把MG 称为命感数。MG 表达的就是感觉函数G(T)在T1至T2生命阶段内对生命的累积。它的几何意义就是对应着T1至T2生命阶段内的感觉函数G(T)与T1至T2阶段的生命值围成的面积。当T1=0,T2=寿命时,MG 则表示了一生的命感数。
令A 为幸福明显界线数,B 为不幸明显界线数。有A>0,B<0。
当MG>0 时,就说明,在T1至T2这个生命阶段里,一个人不管是什么、做了什么、碰到了什么、有什么事情发生了变化、在什么地理位置上都无关系,最终的结果只有一个,那就是他自己的感觉在这个生命阶段内的累积是好的,或是很好的。当MG ≥A 时,他就会说自己在这一段时间里(实际上是在这一段生命里)很幸福。
当MG< 0 时,就说明,在T1至T2这个生命阶段里,一个人不管是什么、做了什么、碰到了什么、有什么事情发生了变化、在什么地理位置上都无关系,最终的结果只有一个,那就是他自己的感觉在这个生命阶段内的累积是不好的,或是很不好的。当MG≤B时,他就会说自己在这一段时间里(实际上是在这一段生命里)很不幸。
什么是幸福?幸福就是感觉对于生命的正累积。
什么是不幸?不幸就是感觉对于生命的负累积。
幸福终于被找到了!不幸也同时被找到了!
展现在我们面前的表达式不仅仅表示了幸福,连同不幸也表达出来了。一个多么惊奇的结果啊!
由此可以看出,幸福和不幸的概念仅仅与生命和感觉有关,与其他无关。
三、命感表达式的一些提示
从MG的表达式中可以看到,不幸也是一种幸福,是负幸福;幸福也是一种不幸,是负不幸。所以幸福和不幸可以统称为广义幸福。
命感表达式MG表达的是广义幸福。即广义幸福就是感觉对生命的累积。
广义幸福值为正时,即为幸福;广义幸福值为负时,即为不幸。因此有:
我们通常说的幸福是狭义幸福,是感觉对生命的正累积;
我们通常说的不幸是狭义不幸,是感觉对生命的负累积。
下面说的幸福和不幸均指的是狭义幸福和狭义不幸。广义幸福需特别指明。
在MG 表达式中,当T1=0,T2=寿命数时,MG 则表示了一个人一生的广义幸福的状态;当0≤T1<T2时,MG 则表示了一个人在T1至T2这个生命阶段里的广义幸福的状态。因此,人具有一生的广义幸福的状态和阶段性的广义幸福的状态。
每一个人都有许多阶段性的广义幸福。生命阶段选取的不同,则对应的广义幸福状态可能不同;一个生命阶段对应的广义幸福状态可以由多个更小的生命阶段对应的广义幸福状态构成,而每一个更小的广义幸福状态也会由于选取的生命阶段不同而可能不同。每一个人只有一个一生的广义幸福状态。
从广义幸福表达式MG 中可以看到,广义幸福只具有感觉和生命这两个构成要素,因此,幸福和不幸的概念也仅仅与这两个要素有关,与获取感觉的方式和维持生命的方式无关。这就给出了一个非常重要的提示:每个人只要选择适合自己的方式来获得感觉和维持生命,让感觉在生命阶段内对生命的累积>0,就获得了幸福;累积的越大就越幸福。
在现实生活里,人们往往苦于不是幸福本身,而是在追求有可能带来幸福的不同工具 (或方式)而已,所以得到的可能仅是工具而未必是幸福,结果与希望相差甚远。这就是人们总是不幸的最根本的原因。
从MG 公式可以看到,在生命阶段里,感觉值不管如何变化,广义幸福值如何变化,但广义幸福值都存在,所以也证明了广义幸福的概念与生命和感觉这两个要素以外的任何因素无关。所以广义幸福的概念与人们的身份和行为无关,但是广义幸福的量值则与人们的身份和行为有关。也就是说,人们的身份和行为的最终作用就是改变了人的寿命值和感觉的瞬时值而已,从而改变了阶段广义幸福值或一生广义幸福值。
四、广义幸福的有关概念
(一)生命和寿命数的定义:把人的生命记为T,单位为岁;把人的寿命记为TS,则把TS称为寿命数。
(二)生命函数的定义:设生命为T,时间为t,若有T=T(t)存在,则把T=T(t)称为生命函数。
定理一,在值域0≤T≤TS内,T=T(t)存在,且有T(t)=t 。
证明:
因为,在人的寿命范围内,每一个生命点都与时间点一一对应,
所以,有T=T(t)存在。
又因为,生命值是可以用时间值来表示的,所以有T(t)=t 。
定理成立。证毕。
(三)感觉的定义
把身体内、外部客观事物和主观意识作用下的生理上的反应称为感觉。
把人的本能乐于接受的感觉称为好的感觉;把人的本能不乐于接受的感觉称为不好的感觉。
(四)正感觉的定义:把好的感觉称为正感觉
负感觉的定义:把不好的感觉称为负感觉。
零感觉的定义:把不好不坏的感觉称为零感觉或无感觉。
(五)感觉函数的定义:设感觉为G,生命为T,在0≤T≤TS内,若 G=G(T)存在,则把G=G(T)称为生命的感觉函数,简称感觉函数。
定理二,在0≤T≤TS内,G=G(T)存在。
证明:
因为,在0≤T≤TS内,对应着每一个生命点都有一种感觉存在,这种感觉或正、或负、或零。
所以,有G=G(T)存在。定理成立。证毕。
(六)可不定积分感觉函数的定义:在0≤T≤TS内,如果有一个函数G1(T)能够精确地等于或最大限度近似等于实际感觉函数G(T),并使不定积分式∫G1(T)dT 存在,则把G1(T)称为G(T)的可不定积分感觉函数。
定理三,在0≤T≤TS内,G(T)的可不定积分感觉函数G1(T)存在。
证明:
因为,在0≤T≤TS内,若G(T)使∫G(T)dT 存在,则有,
G(T)=G1(T),则定理成立。
若G(T)不能使∫G(T)dT 存在,则用近似的方法,通过选择一段或多段曲线或直线来最接近原来的感觉函数G(T),将新选的函数记为G1(T),并使∫G1(T)dT 存在。G1(T)则是G(T)的可不定积分感觉函数,并存在。
定理成立。证毕。
(七)用G1(T)表示G(T)的定义:用G1(T)代表G(T),并重新记为G(T)
新G(T)的意义:新G(T)等于或近似等于原实际感觉函数,并且能够使∫G(T)dT 存在,便于以后进行定积分的计算。
(八)命感函数的定义:设生命为T,有0≤T≤TS,感觉函数为G(T),把mg=∫G(T)dT 0≤T≤TS称为命感函数。
(九)命感数的定义:设生命为T,有0≤T≤TS,感觉函数为G(T),
(十)幸福和不幸的再定义
幸福的再定义是:某一段生命内的幸福就是感觉函数对该段生命进行的正定积分。幸福的判定标志就是MG>0。
不幸的再定义是:某一段生命内的不幸是感觉函数对该段生命进行的负定积分。不幸的判定标志就是MG<0。
这里的幸福和不幸的定义与前面的幸福和不幸的定义的含义是分别对应一致的。
零命感状态的意义:零命感状态有两个含义,第一含义是说,在生命的某个阶段内,幸福值和不幸值抵消了;第二个含义是,在生命的某个阶段里没感觉了(即感觉值均为零)。
(注:平均感觉是一个水平线段。)
(十三)最大感觉值和最小感觉值的性质:因为在每一个人的一生中一定会有感觉好的时刻和感觉不好的时刻,所以有最大感觉值G(T)max>0,最小感觉值G(T)min<0 。
(十四)感觉值单位的定义
则把m/100 称为1 个感觉单位,记为1 感。
现在可以用个人自己的感觉最大值和最小值来确定。
将来幸福测量学发展成熟以后,可以测量出人们的瞬时感觉值来,可以确定一个统一的感觉值单位。
(十五)命感值的单位
把1感×1秒=1感秒,称为1个命感值单位,记为1感秒。以此类推出:1 感时;1 感天;……1 感年(岁)等等。
五、感觉函数的应用
为了准确地反映自己的感觉函数,最好的办法是做记录,除了通常的内容外,最好加上自己这一天的平均感觉值的记录(注:时间段选择的越短,绘制的感觉函数曲线越准确,但是工作量就越大)。感觉值的单位可以自己确定,最好选择一个曾经经历过的有最大绝对值地感觉值得绝对值作为100 个感觉单位,其他的感觉量值跟它进行比较,确定一个数即可。
由于现在没有办法用同一个标准来测量不同人的感觉值,所以选择适合自己使用的单位即可。如果将来可以用同一个标准来测量不同人的感觉值时,再统一感觉值的单位。
例1:设下图是某人到目前为止的感觉函数的曲线图。
横坐标轴是生命轴,单位是岁(或年);竖坐标轴是感觉函数轴,单位是感。
下表给出了每一岁的感觉值与岁数对应的关系。
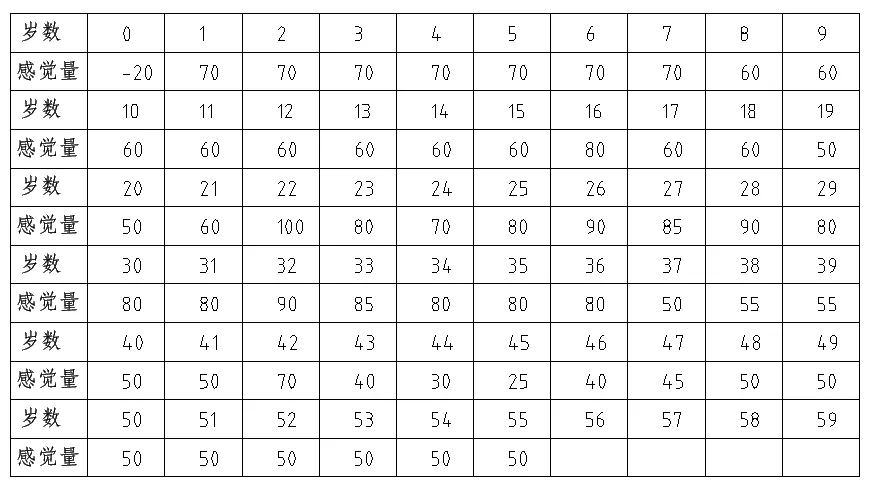
A 点是过去所有感觉的最高点,令其值为100 感,其他的感觉值是比较给出的。
例2:设下面是某人某一个月的感觉函数的曲线图。
横坐标轴是生命轴,单位是日;竖坐标轴是感觉函数轴,单位是感。
下表给出了每一日的感觉值与日对应的关系。
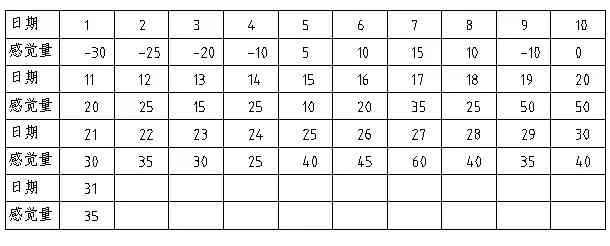
例3:设下面是某人某一个月的感觉函数的曲线图和表。
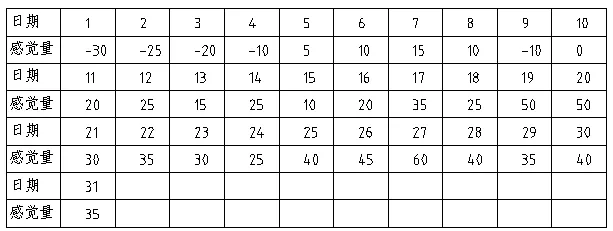
曲线上各点与日期对应关系为:

(1)计算A 点到B 点的平均感觉值:有
A 点到B 点的平均感觉值为-4.4 感。
(2)计算C 点到D 点的平均感觉值:有
C 点到D 点的平均感觉值为38.8 感。
(3)计算A 点到E 点的平均感觉值:有
A 点到E 点的平均感觉值为21.4 感。
由上面计算可知,生命阶段选择不同,对应各阶段的平均感觉值可能不同。
六、命感数的应用
下面计算不同生命阶段的命感数。
例1:设下面是某人某一个星期日在早上6 点到晚上9 点期间的感觉函数的曲线图和表。
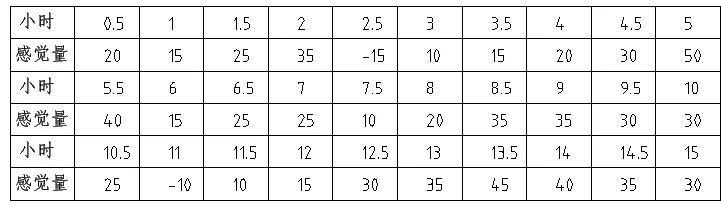
(1)计算第2 时到第3 时的命感数:有
第2 时到第3 时的命感数为3.8 感时。所以说在第2 时到第3 时之间是幸福的。
(2)计算第2.5 时到第3 时的命感数:有
第2.5 时到第3 时的命感数为-1.25 感时。所以说在第2.5 时到第3时之间是不幸的。
(3)计算第2.5 时到第6 时的命感数:有
第2.5 时到第6 时的命感数为82.6 感时。所以说在第2.5 时到第6时之间是幸福的。
由上面计算可以看到,生命阶段选取的不同,对应的命感数也不同。也可能幸福,也可能不幸。
所以说,暂时的不幸不算什么,只要生命存在,我们不断努力,将有更多的机会获得幸福。
七、小结
本文通过幸福存在的普遍性找到了构成幸福的二要素:感觉和生命;通过幸福的抽象性找到了幸福的数学表达式;同时找到了不幸的数学表达式;统一了广义幸福的概念。
给出了幸福的定义、不幸的定义、广义幸福的定义。
给出了幸福学中感觉的定义。
建立了广义幸福有关的一些基本概念;给出了感觉函数和广义幸福的量纲。给出了感觉函数和广义幸福公式应用的计算案例。
