不同巷道断面形态下围岩力学性能研究
2021-10-11姬书强
姬书强
(潞安集团 蒲县隰东煤业有限公司,山西 临汾 041200)
巷道是井下生产的重要运输通道,选择合理的巷道断面,不仅对矿业的经济效益产生重要的影响,还直接关系着矿业的生产安全。由于井下巷道纵横交错,且开拓掘进形式各异,进而巷道的设计对安全尤为重要[1-2]。因此,研究巷道形状对围岩的力学重分布特征,对巷道的安全设计具有重要的作用[3-5]。
在岩层中,巷道掘进对围岩的应力重分布具有重要影响,而巷道断面形状是重要的影响因素之一。为研究巷道围岩在各种形状断面下的力学效应,众多学者采用不同的方法对不同断面围岩应力、变形开展了大量研究[6-7]。李桂臣[8]、冯伟[9]、孟庆彬[10]采用FLAC软件,数值计算了6种断面形状的巷道围岩应力分布、位移分布及塑性区分布等,通过对比分析得到了深部巷道围岩的最优断面形状——圆形断面或椭圆形断面。陈新年[11]、李海军[12]、崔立文[13]、侯化强[14]采用理论分析和相似模拟试验的方法,数值分析了矩形断面巷道围岩的力学特征,同时,研究了围岩松动区受巷道矩形断面形状影响的围岩变形规律。
本文采用有限元工程软件Abaqus,开展了不同巷道断面形状对围岩力学性能的影响研究,分析其力学分布规律。
1 巷道断面形状数值模型
1.1 数理模型的建立
本文分别选取矩形巷道断面、梯形巷道断面、不规则巷道断面、直墙圆拱形巷道断面、椭圆形巷道断面和圆形巷道断面等6种巷道断面周围的应力应变分布情况进行数值模拟研究,巷道断面尺寸如图1所示。其中,前3种断面形态为折线形断面,后3种断面形态为曲线形断面。
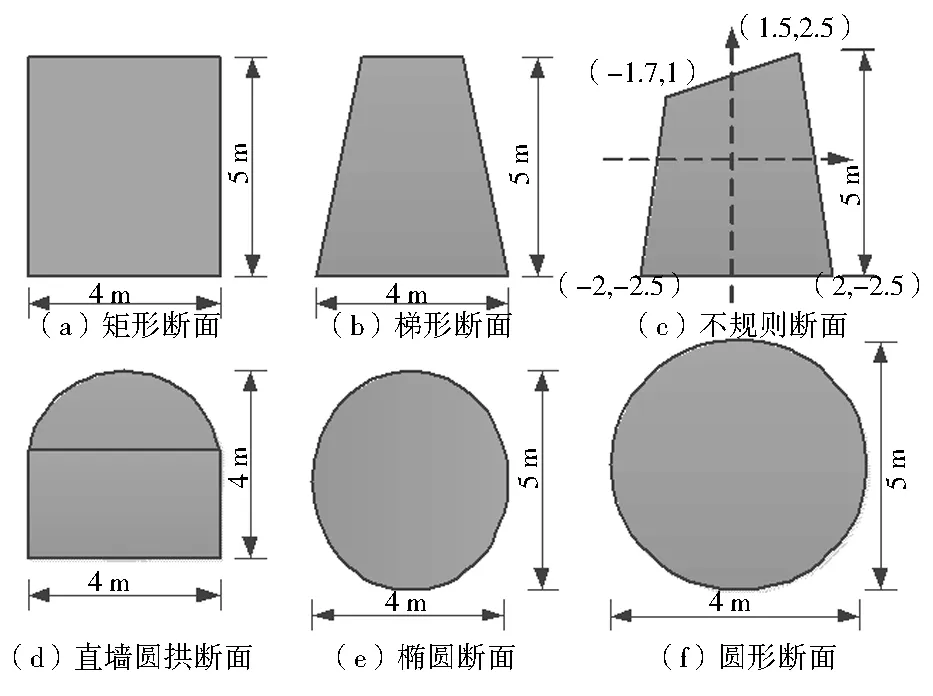
图1 巷道断面尺寸
有限元计算模型采取位于地面以下约500 m深度的均匀岩体,选择的模型尺寸为40 m×40 m,巷道位于模型的中间部位。根据实际情况,将模型近似简化为平面应变模型,如图2所示,在模型的上表面施加局部荷载,以模拟煤层深度所在环境的地应力,约束两侧的水平方向位移和底部的竖向位移,岩体基本力学参数见表1。忽略地质构造中的褶曲及断层等因素影响,根据岩层的深度和重度,在模型上表面施加11 MPa的均布荷载(埋深500 m)。模型底部位移为零,即底部为固定边界。

图2 模型示意

表1 岩体的物理力学参数
1.2 煤岩力学模型准则
本部分主要论述数值计算过程中运用到的屈服函数,根据弹塑性力学理论,当材料内部应力使屈服函数大于零或等于零时,说明材料进入塑性屈服阶段,会产生塑性应变,产生塑性区。
鉴于煤岩体力学特征的复杂性,建立简化的弹性-理想塑性物理模型,本文选择摩尔-库仑屈服准则。拉应力封闭区:
(1)
屈服面:
(2)
压应力封闭区:
(3)
基于弹性流动法则,建立塑性应力-应变的本构关系为:
dεij=cεpdσij
(4)
式中:cεp为弹性塑性矩阵。a、k为屈服函数,表示岩石强度,可由粘聚力C和内摩擦角φ表示为:
(5)

(6)

2 巷道围岩力学特征模拟结果及分析
2.1 Mises应力
Mises应力的表达式为:
式中:σ1、σ2、σ3分别为第一、二、三主应力。Mises应力作为材料内部应力状态的一个综合指标,应力分量表达式为:
不同断面Mises应力变形云图如图3所示。从图3可以看出,无论巷道是何种断面形状,断面附近巷道围岩的应力普遍比较大,应力峰值主要集中在断面的两帮,应力值从两帮向四周逐渐减小,形成“蝴蝶翅膀”形状。同时,不规则断面造成应力重分布的影响区域远大于其他断面,而椭圆形断面和圆形断面的应力影响带最小,如图4所示。从断面变形可以看出,折线形巷道断面更容易被挤压成向内凸的变形,而曲线形断面巷道抵抗这种变形的能力较强,即变形较小,发生应力集中的最大值也较大。在实际情况中,必须加强对容易内凸变形区域的支护。
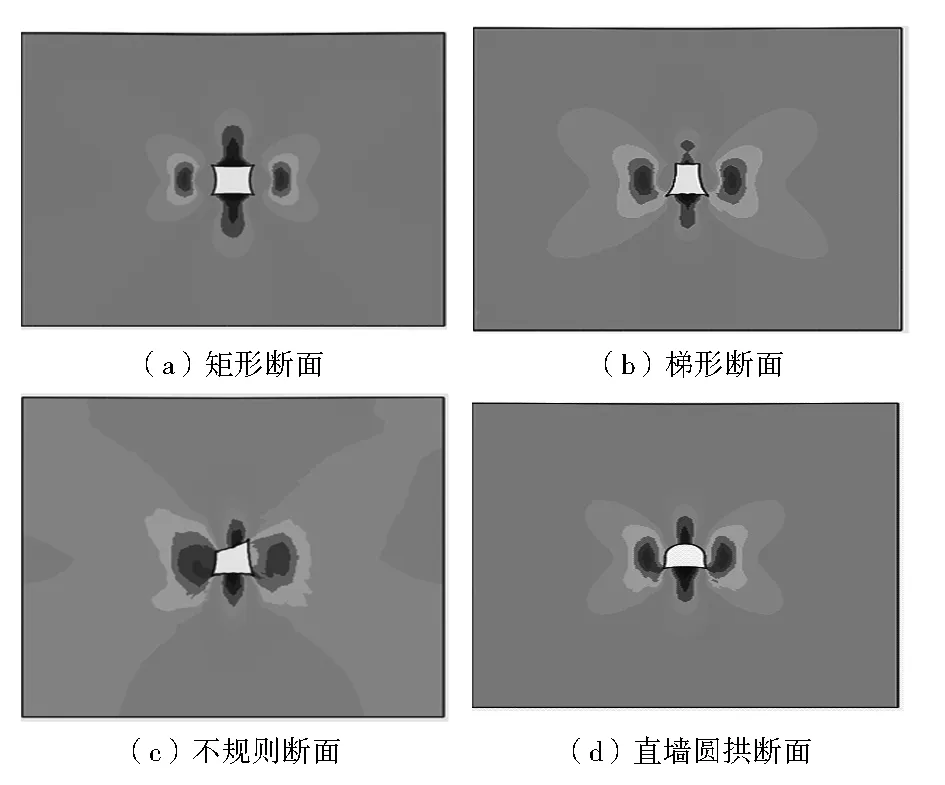

图3 不同断面Mises应力变形云图

图4 断面形状与最大Mises应力
2.2 最大主应力和最小主应力
不同断面最大、最小主应力云图如图5~图6所示。由图5可知,断面的顶板、底板以及两帮的轴线上受影响较大,其中两帮主应力值较大。而且曲线形断面形状的最大、最小主应力峰值分布范围要大于折线形断面,见表2。


图5 不同断面最大主应力云图
2.3 塑性区分布

式中,εp1、εp2、εp3分别为3个方向的主塑性应变。当材料内部任一点等效塑性应变大于零时,即可认为该点进入塑性区。

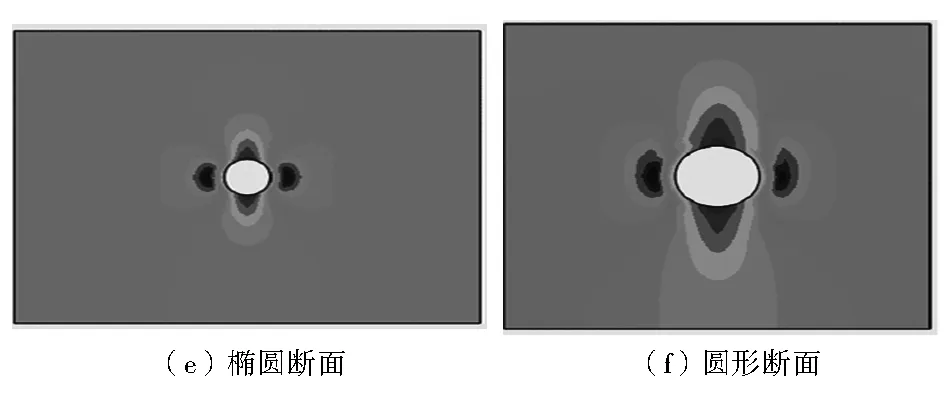
图6 不同断面最小主应力云图

表2 最大、最小主应力峰值范围 MPa
分别对不同断面形状的巷道围岩等效塑性应变(PEEQ)进行计算分析,如图7所示。


图7 不同断面塑性区分布云图
从图7可以看出,巷道围岩的塑性区主要集中在断面的两帮,并从巷道两帮逐渐向外扩展,但断面形状不同,塑性区的扩展形态也不同。其中折线形断面中,折点处向煤层延伸出现相对较长的塑性区。图8为不同断面形状巷道围岩的PEEQ最大值,圆形断面形状的PEEQ最大值最大,而不规则断面的PEEQ最大值最小。

图8 断面形状与最大PEEQ值
3 结 语
本文采用有限元工程软件,开展了不同巷道断面形状对围岩力学性能的影响研究。结论如下:
1) 断面附近巷道围岩的应力普遍比较大,应力峰值主要集中在断面的两帮,应力值从两帮向四周逐渐减小,形成“蝴蝶翅膀”形状。
2) 在荷载作用下,曲线形断面巷道变形较小,发生应力集中的最大值也较大。
3) 曲线形断面形状的最大、最小主应力峰值分布范围要大于折线形断面。
4) 巷道围岩的塑性区主要集中在断面的两帮,并从巷道两帮逐渐向外扩展。
