基于FLUENT的多油腔动静压轴承油膜压力仿真∗

刘汉阳 李钦奉

（江苏科技大学机械工程学院 镇江 212003）

1 引言

在现代化机械制造业发展的时代，旋转机械向着高速、重载方向发展，特别在汽车制造、船舶制造、航空航天等领域旋转机械的应用变得越来越广泛。旋转机械中最核心的零部件是轴承，其在运转系统中承担着重要的角色，又被称为机械的关节［1］。目前，大多数学者研究轴承静动态特性都是基于数值计算法来求解雷诺方程。雷诺方程是由N-S方程简化而来的，其忽略了惯性项等因素的影响［2］。数值计算法只适用于形状简单的轴承，对于一些形状复杂的轴承需要花费更多的精力和时间。计算流体动力学的基本原理是将物理量场划分为一个个离散的单元，然后在单元上建立代数方程组，最后对代数方程组进行求解，得到物理变量的近似解［3～4］。大型商用计算流体动力学（Computational Fluid Dynamics）软件FLUENT在流体计算方面有着巨大的优势，它能直观反映出流体的流动状态并实现了轴承在运转过程中油膜的可视化。

近年来，国内外学者通过数值计算和仿真研究了轴承在运转过程中油膜的特性。孟曙光等［5］基于有限体积法的计算方法，针对深浅腔动静压轴承，研究了供油压力、主轴转速、浅腔深度、初始油膜厚度、进油孔径、等参数对深浅腔动静压轴承承载特性的影响规律。GUO Zeng-Lin等［6］比较了CFX TASCflow和VT-EXPRESS两种方法在仿真轴承运转时油膜上最大压力的异同，并验证了仿真的合理性。马涛等［7］针对多油腔动静压轴承流体流动的复杂性，使用FLUENT软件研究了轴承轴承内部的压力场。黄首峰等［8］通过FLUENT软件仿真了偏心率和转速对油膜压力的影响。刘豪杰等［9］对深浅腔动静压轴承的油膜压力进行了仿真，主要研究了偏心率和转速对油膜压力的影响。赵春明等［10］仿真了转速对液体静压轴承润滑油膜压力的影响。王丽丽等［11］比较了润滑油在等黏度和黏度变化情况下的油膜压力变化。张晓斐等［12］仿真了轴承在不同接触位置下供油压力和转速对轴承润滑油膜压力分布的影响。

前人的研究大都是基于外部因素的变化对最大油膜压力的影响，忽略滑动轴承本身的结构，本文在前人研究的基础之上，基于CFD的基本理论，利用FLUENT软件对普通圆柱四油腔动静压轴承进行仿真，其结构如图1所示。研究了转速、供油压力、进油口直径对油膜压力的影响。

图1 普通圆柱四油腔动静压轴承结构图

2 CFD控制方程与仿真模型的建立

CFD控制方程指的是自然界中流体在流动的过程中需要遵循的物理规律。较常用的控制方程有连续性方程、动量守恒方程、能量守恒方程。因为本文中研究油膜压力，不涉及能量的变化，所以流体在运行的过程中需遵循连续性方程和动量守恒方程。

1）连续性方程

连续性方程又称为质量守恒方程，指的是流体的流入或者流出与系统质量的增加或者减少是相等的。

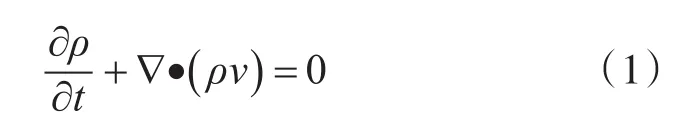
式中：v为速度矢量；ρ为密度；t为时间。

2）动量守恒方程

动量守恒方程又称为纳维-斯托克斯方程，主要是用来描述粘性不可压缩流体动量守恒的运动方程，本文中的润滑油为粘性不可压缩流体。

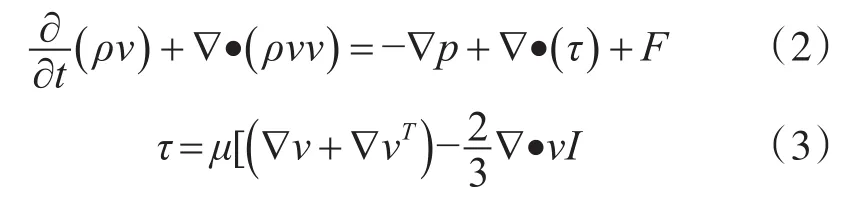
式中：p为流体微元体上的压力；F为外部体积力；τ为应力张量；I为单位张量。

3 动静压滑动轴承仿真模型建立与仿真设置

3.1 仿真模型建立

本文研究对象是普通圆柱四油腔动静压轴承，轴承上设有四个进油口，轴瓦内部有四个大小相等的油槽，储存润滑油。其结构参数来自参考文献［6］，具体参数如表1所示。根据表1的结构参数，采用三维设计软件UG建立油膜的三维模型，将油膜三维造型导出为Parasolid格式，为后续的分析奠定基础。

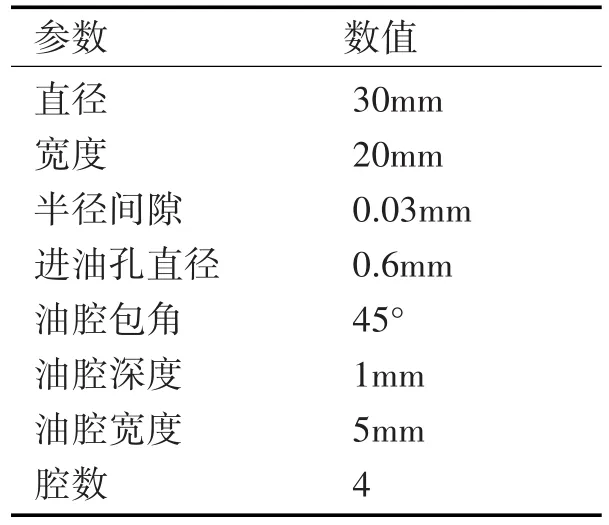
表1 普通圆柱四油腔动静压轴承结构参数

3.2 油膜网格的划分

本研究主要在ANSYS WORKBENCH中完成，将建立好的油膜三维模型导入到ANSYS Mesh中进行网格划分。因为本研究的轴承有油槽和进油口结构存在，油膜的形状是阶梯形状，所以需要先将油膜的结构进行分割操作，然后再进行网格划分。比起油膜的宽度和半径，其厚度非常小。如果直接采用非结构化网格，容易造成单元体积为负和网格扭曲，所以本次研究划分的网格采用结构化六面体网格。在对油膜进行网格划分时，将轴向取200个节点，周向取200个节点。油膜径向的尺寸相对于周向和轴向是非常小的，此油膜模型的网格质量和网格数主要由径向网格数量决定，所以取径向网格层数为 4、5、6、7、8进行网格独立性验证。取偏心率0.5，供油压力4MPa，转速6000r∕min，进油口直径0.6mm进行计算，不同网格数量的计算结果如表2所示。根据计算结果发现随着网格数的增加，油膜最大压力变化较小，综合计算资源和时间的考虑，选择方案2的网格配置。网格质量评价的标准为歪斜率，歪斜率越接近0表示理想网格，也就是统计图越靠近左边。油膜网格示意图如图2所示，网格质量如图3所示。

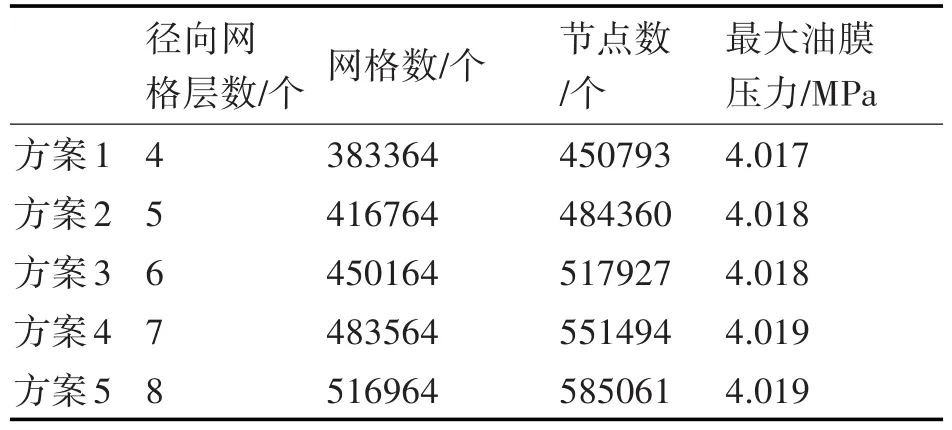
表2 不同网格数量的计算结果

图2 油膜网格示意图

图3 网格质量统计图

3.3 模型的假设与求解设置

在进行仿真计算时，做出如下的假设。

1）在滑动轴承内部流场中，将流体假设为不可压缩流体并且流动状态为三维定常流动。

2）忽略润滑油的惯性力，并且油膜边界压力为0。

3）润滑油在轴承内部流动时，经过雷诺数计算Re<2300，所以流动状态为层流。

4）润滑油与轴径轴瓦接触无相对滑移。

FLUENT求解时设置如下：

1）流动状态设置为层流。

2）润滑油的密度为ρ=870kg/m3，动力粘度μ=9.93×10-3Pa·s。

3）四个进油口设置为流入，轴径设置为旋转，轴瓦边界固定，轴承两端出油，出油压力等于标准大气压力。

4）求解的方法设置为SIMPLE，残差设置为1e-6，迭代步数500步。

4 仿真结果与分析

4.1 转速对油膜压力的影响规律

普通圆柱动静压轴承在工作时，轴承上承载了一定的载荷，载荷的作用会使得轴承的中心和轴径的中心产生一定的间隙，从而会形成偏心。本文将轴承的偏心率设置为0.5，供油压力4MPa、进油口直径 0.6mm，探究转速 3000r∕min～9000r∕min 对油膜最大压力的影响，得到如图4所示的油膜压力大小分布随转速变化的云图。

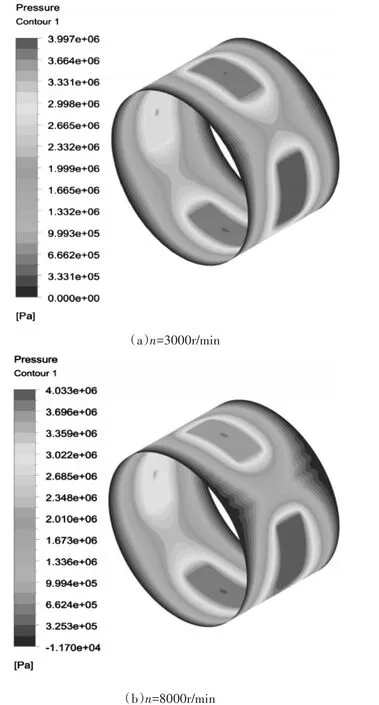
图4 转速变化仿真云图

从图4可以发现油膜上的压力存在楔形收敛区和发散区。油膜上的最大压力主要集中在四个油腔中，油膜上的压力大小分布从四个油腔逐渐向两端面减小。在轴承转速较低的时，静压效应起主要的作用，此时油膜上的压力较低。随着轴承的转速升高，动压效应逐渐增强，此时油膜上的最大压力也在变大。在其他参数不变的情况下，改变轴承的速度大小，从图4还可以发现，随着速度的增大，油膜上的最大压力值也在逐渐增大。当转速达到8000r∕min左右时，油膜上出现了负压区域。

根据仿真结果得到如图5的变化规律，在普通圆柱动静压轴承的偏心率、供油压力和进油口直径一定的情况下，油膜上的压力和轴承的转速成正比。但当转速达到8000r∕min左右时，此时油膜上的压力出现负压区域，在如此高的转速下，油膜会存在破裂的危险，在实际工作时要严格控制轴承的转速，避免损伤轴承。

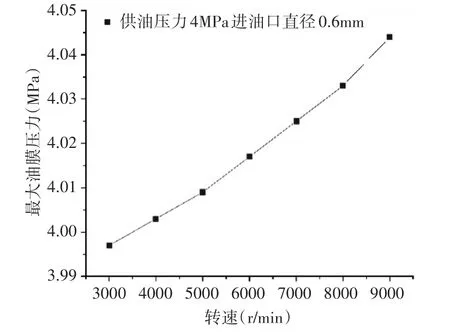
图5 转速-油膜最大压力变化规律图

4.2 供油压力对油膜压力的影响规律

在轴承运转时，轴承的结构参数是固定不变的。除了轴承的转速会影响油膜的压力大小分布，供油压力同样也会影响其大小。在偏心率为0.5时，选择轴承的转速为6000r∕min、进油口直径0.6mm，对供油压力3MPa～6MPa进行仿真分析，得到如图6所示的油膜压力大小分布随供油压力的变化云图。

从图6发现当供油压力为3MPa时，油膜上出现了负压区域。这主要是因为在转速一定时，供油的压力较小，不能及时给轴承中提供足够的油，导致油膜上形成负压区。从图6中还可以发现当供油压力变大，达到4MPa的时候，油膜上负压消失。

图6 供油压力变化仿真云图

根据仿真结果得到如图7的变化规律，在普通圆柱动静压轴承的偏心率、转速和进油口直径一定的情况下，油膜上的压力和供油压力成正比。但是供油压力过小，油膜会形成负压区，这不利于滑动轴承的润滑，所以要避免供油压力过小而导致轴瓦和轴径直接接触，发生磨损。在供油压力为4MPa时，油膜上的负压消失了，说明合理地增大供油压力有利于轴承的润滑，但是供油压力过大容易导致供油管道发生泄漏的危险，所以在轴承承载力满足条件的情况下，要合理地选择供油压力。

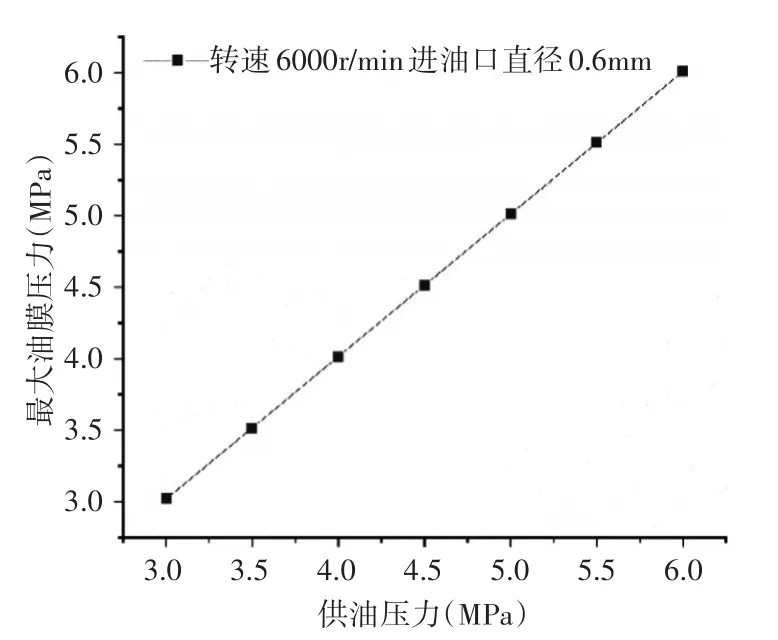
图7 供油压力-油膜最大压力变化规律

4.3 进油口直径对油膜压力的影响规律

本文除仿真转速和供油压力之外，还对滑动轴承的进油口直径大小进行了仿真。在偏心率0.5、转速6000r∕min和供油压力4MPa的情况下，研究直径大小为0.4mm～1mm的节流小孔对油膜压力大小分布的影响。

从图8中发现，油膜最上方油槽处的压力随着进油口直径的变大也在慢慢的变大；从图8中还可以发现，在直径为0.4mm时，油膜上出现压力为负的区域，但是随着直径的慢慢变大，油膜上的负压区域消失。综合比较图8中油膜上最大压力发现，随着进油口直径的增加，油膜最大压力刚开始变化趋势较大，但当进油口直径为0.8mm以后，最大油膜压力变化不是非常明显。

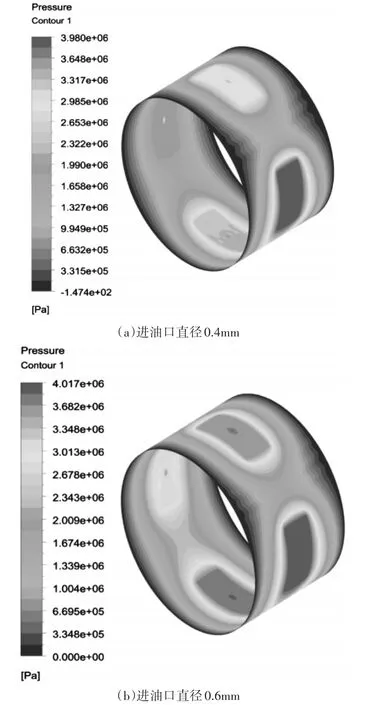
图8 进油口直径变化仿真云图

根据仿真结果得到如图9的变化规律，在普通圆柱动静压轴承的偏心率、转速和供油压力一定的情况下。油膜上的最大压力与进油口直径近似于正比的关系，但当进油口直径为0.8mm后，最大油膜压力的变化幅度有限。当进油口直径变大时，相应的进油的流量也会变大，那么会使回油变得更加困难，造成漏油的意外，所以在油膜的承载力达到适用范围内，进油口直径不宜选的过大。将本文研究得到的最大油膜压力随进油口直径变化规律与参考文献［5］基于有限体积法的数值计算得到的结果进行对比验证，发现其变化曲线与本文研究得到的曲线变化规律吻合度较好，证明了本仿真的准确性。

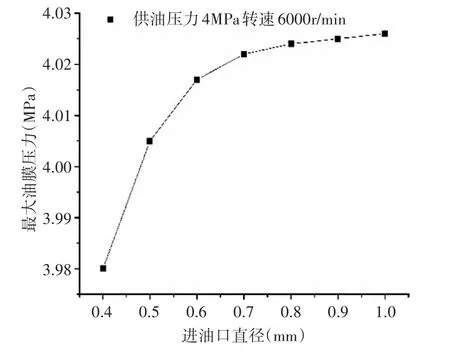
图9 进油口直径-油膜最大压力变化规律

5 结语

本文利用了CFD软件FLUENT对普通圆柱多油腔滑动轴承进行了仿真分析，计算得到了转速、供油压力和进油口直径对油膜压力的影响规律分布，主要得到以下结论。

1）在偏心率、供油压力和进油口直径一定的情况下，转速和油膜压力呈现正比的变化规律。但过高的转速会使得油膜上形成负压，造成轴径和轴瓦的直接接触加快轴承的磨损，所以在轴承达到承载力范围内，要合理地控制轴承转速。

2）在偏心率、转速和进油口直径一定的情况下，供油压力和油膜压力成正比的变化规律。过低的供油压力会在油膜上形成负压，过高的油膜压力会使油管发生泄漏，所以在轴承保证足够承载力的条件下，供油压力要选择合理。

3）在偏心率、转速和供油压力一定的情况下，进油口直径和油膜压力的变化规律先呈现正比的关系，随着直径的增大，油膜最大压力趋于平稳。