基于Abramovich射流理论的飞机尾流数值模拟∗

潘卫军 张衡衡 殷浩然 王 昊 王 玄

（中国民航飞行学院空中交通管理学院 广汉 618307）

1 引言

机场中跑道是飞机起飞和降落的场所，随着航班数量的增多，飞机起飞和降落的时间和距离间隔不断缩小，而飞机降落过程中产生的尾流消散则需要一定的时间，由此就会导致一些飞机将处于前机的尾流中，使后机的性能受到影响，小则影响后机降落的操纵性能，大则会导致后机产生滚转，使飞机失去控制。通过研究前机尾流对后机的影响，合理的缩减前后机的尾流间隔，提高机场等终端区的运行效率。

2 模型基本定理

所有自然现象都可以用质量守恒定量、能量守恒定律以及动量守恒三大守恒定律解释，飞机湍流运动作为流体运动中的一种，因此三大守恒定律方程也适用于此。

2.1 质量守恒方程

质量守恒定律可以表示物质不论发生什么变化和过程，物质的总质量保持不变。该守恒方程可用式（1）表示：

式（1）中：S为参与变化和某种过程的物质总质量；Τ为变化或过程时间；ν为速度矢量；ρ为流体密度。

2.2 动量守恒方程

动量守恒定律可表示为作用在该微元体上的外力为零或外力矢量和为零。动量守恒定律可用式（2）表示：

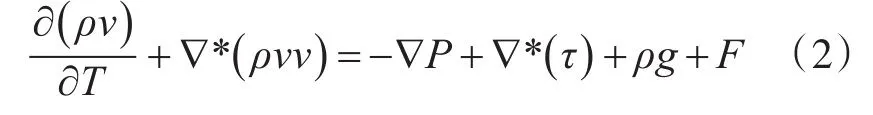
式（2）中各符号含义：F为外部体积力；Ρ为静压力；g为重力体积力；τ为黏性应力张量。

2.3 能量守恒方程

能量守恒定律可表示为微元体作为孤立系统时总能量保持不变。该守恒方程的数学表达式为式（3）。

在求解上述三大方程时通常应用直接数值模拟和非直接数值模拟的方法，由于直接数值模拟要求在小湍流下进行，所以计算量很大，此方法目前只应用在求解低雷诺数的流体问题上，非直接方法则要求简单，因此经常用作计算流体模型的方法，通常包括大涡模拟、雷诺平均和统计平均三种子方法［2］。

目前建立的飞机尾流模型有S-A模型，k-ε模型和k-ω SST模型。随飞机的向前平飞，尾流区的湍流速度逐渐下降。经过一段距离后，在周围气流作用下，风速逐渐恢复。上述这些模型不能较准确描述飞机尾流速度衰减和逐步恢复的整个过程。而采用Abramovich（1963）射流理论建立飞机全场尾流模型（简称AV尾流模型）能较准确地模拟此过程。本文将使用基于Abramovich（1963）射流理论建立的尾流模型对飞机尾流进行建模，并分析尾流的衰减和耗散趋势［3］。

3 基于射流理论的尾流模型

AV尾流模型是在Abramovich（1963）射流理论基础上发展的一种全场尾流模型，在使用AV尾流模型分析尾流区的速度特性过程中，首先根据尾流区的扩散特点将尾流区分不同阶段，在不同阶段，尾涡的扩散受到自身强度和背景风场的影响，大雷诺数无边界约束的自由湍流会与边界上活跃的大气混合将周围气流卷吸进来并不断扩大，在此过程中尾涡的强度因不断吸入周围气流消耗能量而环量减小，一段时间后，湍性射流则可用边界层理论进行计算分析。如图1所示，在静止流体中存在一不可压缩平面湍性射流。其轴向平均速度ū（x，y）不等于零，整个区域由中心轴线和上下两个“边界层”组成，在图1中理论边界由虚线表示，因此定常平面湍性射流与湍流边界层方程组近似成立，式（4）为湍流边界层方程组。

图1 平面湍性射流

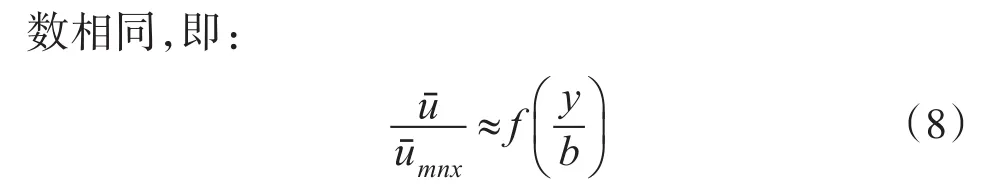
根据以上方程，H.赖夏特等进行了完整的理论分析。其主要结论为

1）射流不同位置处的宽度与该位置到射流源的距离成正比，如果忽略雷诺数的影响，此射流大约以13°半角向后扩张；

2）射流速度分布为

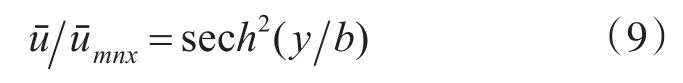
3）射流轴线上的最大速度与到射流出口的距离的平方根成反比。

飞机尾流要比不可压缩流体的常压自由射流更复杂。飞机尾流的形成如同气流在旋转发生器中高速喷出，旋转向后喷向一个无边界空间，即旋转射流。旋转射流中既有直流射流的轴向分速和径向分速，又有一个切向分速，而且其径向分速比直流射流中的径向分速大得多。

根据实验得出，自由旋转射流的任一截面上，旋转动量矩和轴向动量矩都为固定常数，即：

式中Gφ为旋转动量矩，Gx为轴向动量通量，Wt和Wa分别为轴向分速和切向分速，P为射流任意断面的静压，R为射流任意断面的半径。

由于这些动量通量可以看成是旋转射流空气动力学的特征，所以可用旋转强度准则或旋转数来表征旋转射流的特性，即：

式中R0为尾流涡核的定性尺寸，一般取其半径，在飞机尾流中，涡核半径约为机翼展长的5%～10%。旋转动量矩Gφ越大，表明气流旋转越强烈；轴向动量矩Gx表示气流向前运动的能力，轴向速度越大，前进能力越强［4］。

实验表明，旋转数S也是由几何上相似的涡核所产生的旋转射流的重要相似准则。旋转射流的轴向和切向速度特征，卷吸量、扩张角和射流的射程等重要参数都与旋转数S有关。当旋转数低于一定数值时，轴向反向压力梯度不够大，不足以引起内部回流，轴向速度均为正值，称之为弱旋转射流。由风洞实验可得，当S=0时，无旋流；S≤0.6时为弱旋流，S＞0.6时为强旋流。飞机尾流一般为 S≤0.6的弱旋流［5］。

3.1 速度变化趋势

旋转射流包括切向速度vθ，轴向速度vx和径向速度vr，流体在旋转发生器中高速喷出后，其三种速度随轴向的变化趋势如图2所示，其中d为翼展宽度，x为某一截面a到涡核的轴向距离。随着增大，当时，切向速度vθ、轴向速度vx和径向速度vr急剧减小，当以后，vθ、vr基本上消失，只有vx存在。如图1为三种速度变化趋势图，其中 A曲线表示 vθmax/vθ，B曲线表示vxmax/vx，C曲线表示 vrmax/vr。

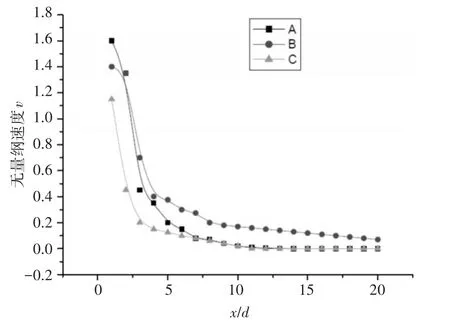
图2 速度变化趋势

3.2 轴向速度分布

在一个切向空气旋转发生器上进行了试验，其结果如图3所示。其中横坐标表示为某一截面a的半径b，纵坐标表示为某一圆形截面a上随半径的增大，轴向速度与该截面a上最大速度的比值，从图3上可以看出，当S值小于0.6时，某一截面上的轴向速度的分布随S值的增大，轴向速度截面的半径越大，且各个S下的轴向速度变化趋势是相似的，而且其分布都服从高斯方程。

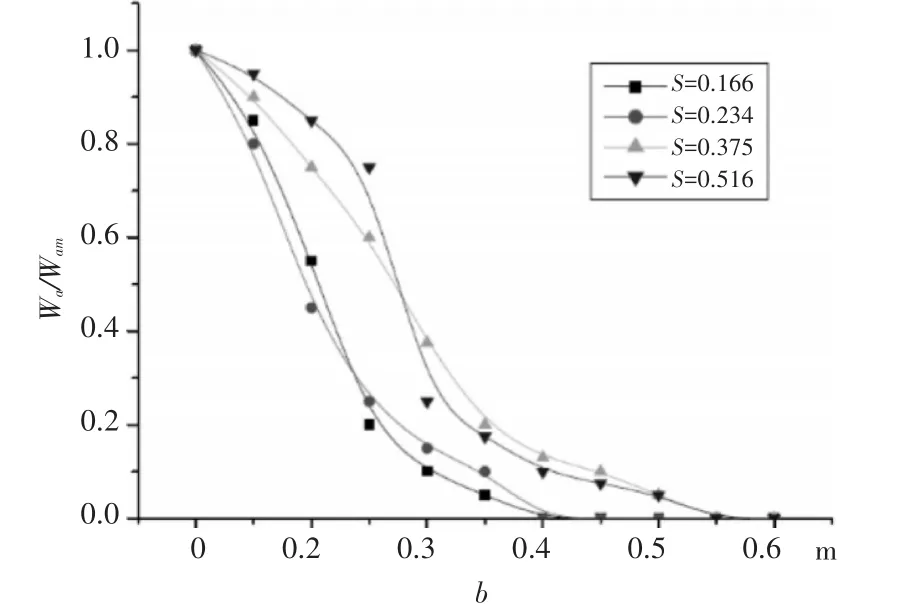
图3 轴向速度分布图

相似的轴向速度分布图满足于如下的指数方程：

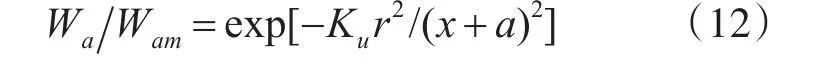
式中Wa和Wam表示某截面任意点上的轴向速度和最大轴向速度；KU为分布常数，它随旋转数而变，由经验公式确定；r为径向坐标；a为涡核原点距离坐标原点的距离。

3.3 切向速度分布

切向速度Wt的径向分布以对r/(x+a)的形式表示在图4上。从该图可以看出，某一截面处从距离涡核两个直径距离起，在所有被研究的旋转数下，切向速度的分布图中变化趋势是相似的。切向速度分布图的内区是线性的，相应于固体物体的旋转特性，也即相应于具有角速度的强制旋涡型流动［6］。

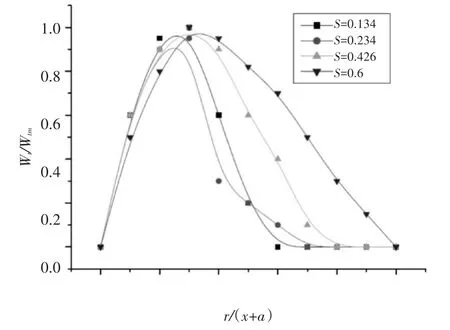
图4 切向速度分布

切向速度分布图的外区相应于常数的自由旋涡型流动，相似的切向速度分布图可以由一个三阶多项式予以描述即：

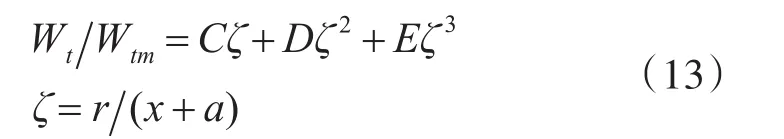
式中C、D和E为实验常数，a为涡核距离坐标原点的距离，r为径向坐标。

3.4 射流速度的衰减

根据理论上的推导，最大轴向速度的衰减和最大切向速度的衰减由下列公式表示：

式（15）中，K1为轴向速度衰减常数；K2为切向速度衰减常数；其中为ξ=r/(x+a)。

轴向速度最大值的衰减情况示于图5上。图中Wamo是x=0处最大值。弱旋转射流的势能能扩张到两个涡核直径的距离，并且在四个直径以后按双曲线规律衰减。衰减常数K1是根据在完全发展区中速度最大值的平均斜率来确定的。

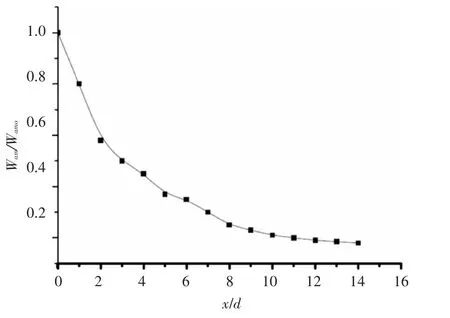
图5 轴向速度最大值的衰减情况

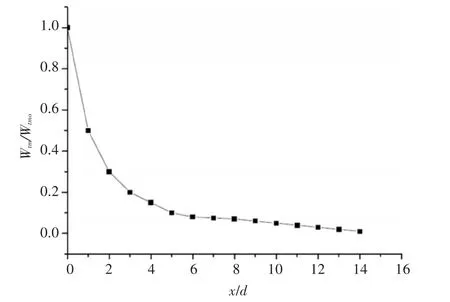
图6 切向速度最大值的衰减图

3.5 射流的扩张角

射流的扩张角α，对弱旋转射流来说是随旋转数S的增加而增加的，它由式（16）确定：

一些人的试验结果指出，射流的扩张角并不一直随S而增加，而趋向于达到某一渐近值。而另一些人的试验指出，α与S是一个线性增加的关系。Chigier等在研究了各个试验者所用的不同的试验条件后指出，如果在旋转发生器孔口的平面上与轴线垂直有一约束的情况，扩张角α就不一直随S的增加而增加。如果没有这样一约束，则α一直随S的增加而增加［8］。

3.6 射流的卷吸

弱旋转射流由于没有中心回流，因而它只是从射流的外侧进行卷吸。通过射流中任一截面的流量都是由对该截面的轴向速度图积分而得到的。试验指出，弱旋转射流的卷吸量既随旋转数S而增加，又随x而增加。即

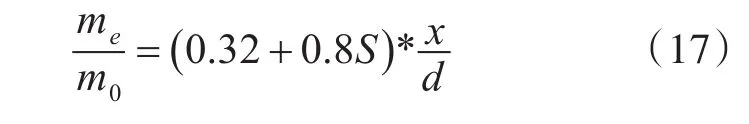
4 基于Abramovich射流理论的飞机尾流分析

以单侧尾涡为例，将飞机尾流区分成三个阶段，如图7所示。在每个耗散阶段，尾流增长速率与自身环量和背景风场有关［9］。

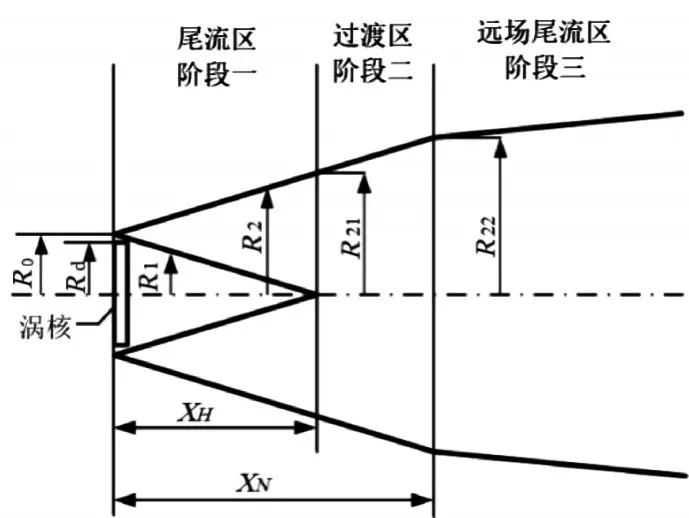
图7 飞机尾流模型几何轮廓图

1）阶段一是飞机近场尾流区，该区域从涡核延伸到锥形均匀流的末端。其尾流增长速率只决定于自身环量，背景风场影响可忽略不计。

2）阶段二是尾流过渡区。阶段二同阶段一有相同的尾流增长速率，它主要决定于自身环量，但是背景风场也将产生一定的影响。

3）阶段三是飞机远场尾流区，自身环量的作用下降，尾流增长速率取决于背景风场的作用。

4.1 阶段一的尾流特性

在基于Abramovich（1963）射流理论的基础上，阶段一的速度剖面可表示为

式中V∞为涡核前自由流风速；V0为涡核后阶段一内的均匀流风速；r为某点到尾流中心旋转轴的距离。

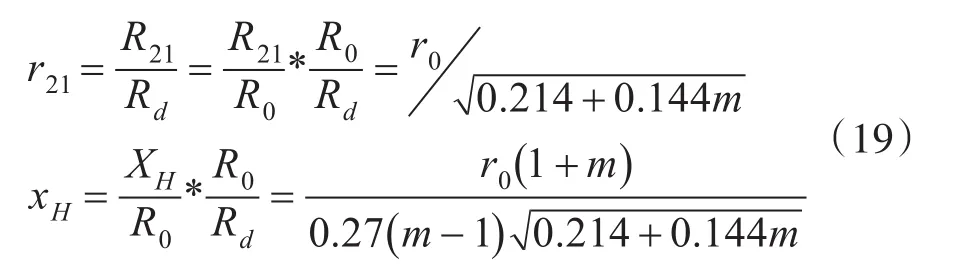
式中r21为阶段一末无量纲化尾流半径，XH为阶段一的长度，R0为初始尾流半径，Rd为涡核半径，r0为无量纲初始尾流半径，m为初始速度比。

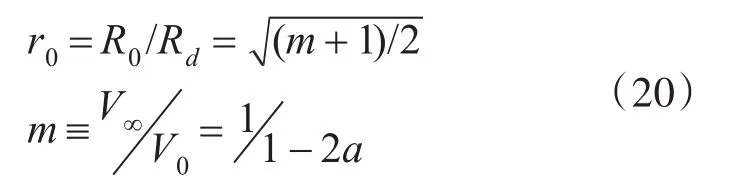
a为尾流轴向速度诱导因子。

阶段一内边界层厚度b为自由流与均匀流之间的距离：

在阶段一末端，r1=0，b=r2=r21，于是由于自身环量引起的边界层增长速率为

背景风场在静止大气和旋转射流中同时存在且影响边界层的两侧，因此边界层增长速率为［10］

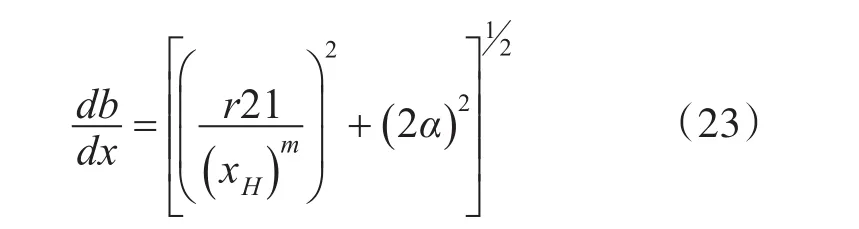
式中α为由背景风场引起的边界层增长速率

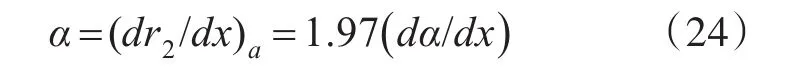
dα/dx与大气边界层中Pasquill稳定级相关，由于阶段一末的尾流半径为r21，则阶段一的长度xH为

4.2 阶段二的尾流特性

根据Abramovich射流理论：

4.3 阶段三的尾流特性

这个区域的尾流增长速率在开始时是由自身环量和背景风场共同决定的，随着x的增加，自身环量的影响逐渐减小到零，尾流增长速率完全决定于背景风场的影响。另外该区域的速度剖面是自相似的，因此在任意x处都有相同的数学表达形式。基于射流理论给出［11］

4.4 各阶段速度剖面

如果x≤xH，则所讨论的区域在阶段一，η＞1时，r在涡核后均匀流核心内v1=1/m；η＜0时，r在尾流边界层外v1=1；0＜η＜1时，r在尾流边界层内：

4.5 基于AV尾流模型模拟的飞机速度剖面

图8和图9是基于Abramovich的尾流模型模拟的尾流速度剖面与瑞典航空研究院（FFA）风洞实验结果的比较，Vc为尾流中心速度损耗，由图8可知；基于Abramovich的尾流模型在一定程度上模拟了飞机尾流区的速度分布；在远场尾流区（x/D=6;x/D=8），尾流半径的计算结果明显比实验结果大，而在尾流影响的主要区域（-0.5＜y/D＜0.5），由于基于Abramovich的尾流模型计算时的背景风场和FAA风洞实验时不同，所以速度的计算结果比实验结果要大。

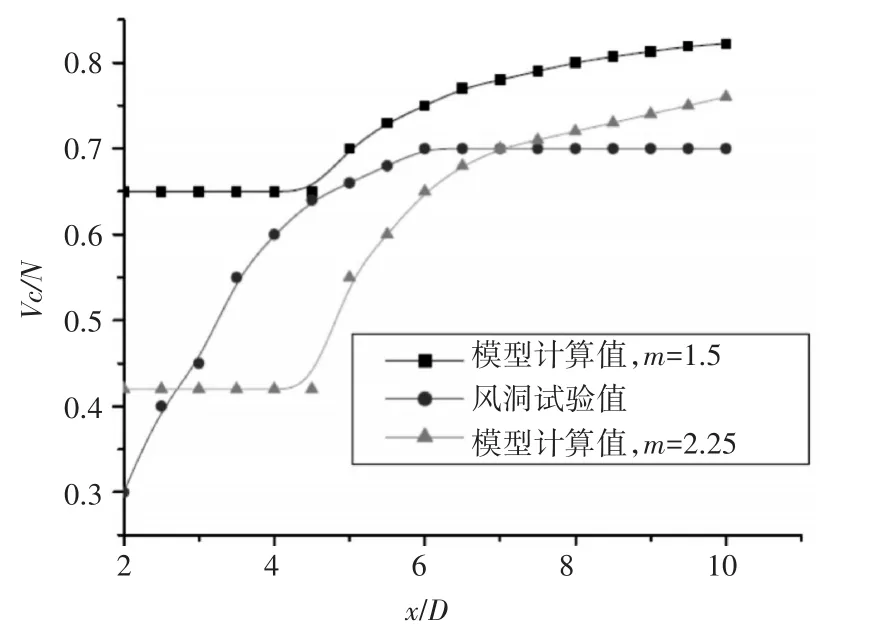
图8 尾流区中心线平均速度分布

图9 尾流区截面内平均速度分布

飞机尾流区内，离涡核越近的截面，速度损失越大，同一截面内，离涡核中心旋转轴线越近，速度损失越大。在所测量的三个截面中，其最大速度损失都出现在涡核轴线上；离涡核越近的截面内，其尾流影响区域稍小一些；尾流区中心线上平均速度随坐标增加而逐渐恢复，在近场尾流区其恢复得更快一些。

5 结语

本文首先针对尾流区内速度和尾流半径的变化规律，利用Abramovich射流理论对尾流区不同区域的切向、轴向和径向速度分布等速度特征进行分析，基于Abramovich的尾流模型的分析对飞机尾流区各区域进行建模，将计算结果与风洞实验结果进行了比较得出：可以用基于Abramovich射流理论的尾流模型来模拟飞机尾流区速度特征分布，计算处于尾流区后机飞行性能。综上所述，基于Abramovich的尾流模型计算尾流区飞机性能是可行的。