基于随机森林算法的水陆联运枢纽客运量预测

王郅翔 王余宽 许小卫 谢新连

【摘 要】 为提升水陆联运枢纽客运量预测精度，选用随机森林算法构建水陆联运枢纽客运量预测模型，选取影响水陆联运枢纽客流的多种因素构建初始数据集;运用随机森林算法对初始数据集进行参数优选，生成初始预测模型;随机扰动特征变量值，对特征变量进行重要性分析，并优选特征变量得出预测数据集;最后，构建水陆联运枢纽客运量预测模型，载入测试集数据预测水陆联运枢纽客运量。将上述方法与三次指数平滑、多元回归分析两种预测方法进行对比，结果表明基于随机森林算法的预测结果更为精确。

【关键词】 水陆联运;枢纽;客运量预测;随机森林算法;特征变量

0 引 言

客运量预测是水陆联运枢纽规划、设计等环节的基础工作，同时又是选定运输模式和船舶班线组织方案的重要参考依据;因此，如何科学合理地预测水陆联运枢纽客运量具有重要的现实意义。

常见的客运量预测方法以时间序列分析法为主，如指数平滑法、多元线性回归法、灰色预测法等。此外，随着机器学习领域的深入发展，越来越多的人工学习算法被应用到客流量预测中，如人工神经网络、支持向量机等。指数平滑法在处理多维变量存在不足，无法同时考虑变量间因果关系;多元线性回归法弥补了指数平滑法在处理多维变量方面的缺陷，但难以处理多重共线性的问题;灰色预测法可应用于类似客流量这种指数增长的数据，但不适用于长期预测;人工神经网络对变量拟合精度高，但存在过拟合现象严重，且在实际运用中，存在建模复杂、适用性差、收敛速度慢等缺陷;支持向量机在处理大规模高维数据时，泛化能力较差，且对数据缺失较为敏感。随机森林（Random Forest）算法具备预测准确、鲁棒性高、可操作性强等优点，且不会过拟合，已被广泛运用于电力、金融、测绘等领域。

本文基于随机森林算法构建一种客运量预测模型，并以某水陆联运枢纽为例，将预测结果与三次指数平滑、多元回归分析预测效果对比，结果表明基于随机森林算法的预测结果更为精确，对水陆联运枢纽及其他客运场站的客运量预测工作具有一定的参考价值。

1 随机森林算法介绍

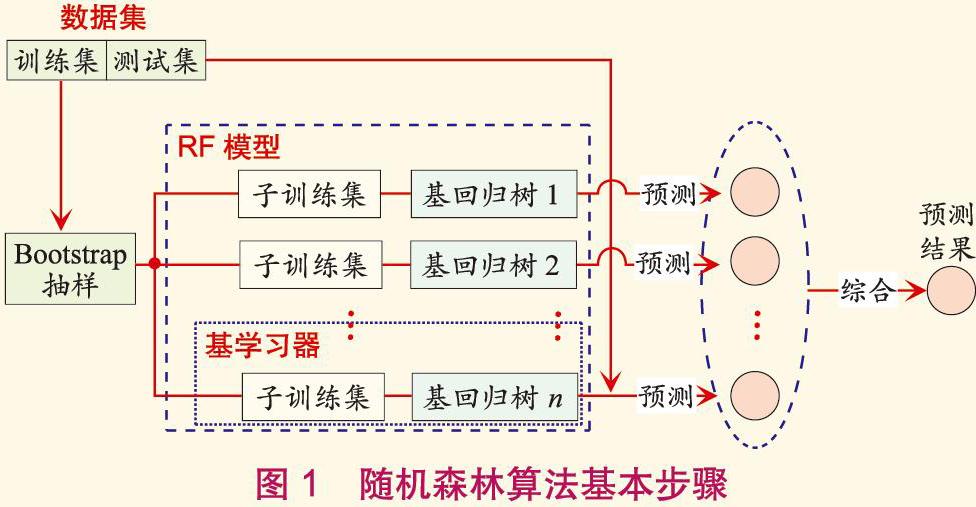
随机森林算法基本步骤（见图1）如下：划分初始数据集为训练集与测试集，用于训练随机森林预测模型及检测预测结果;采取自展法（Bootstrap）抽样对训练集进行随机有放回抽样，形成n个子训练集;针对每一个子训练集生成一棵决策树，每棵决策樹仅对子训练集数据进行回归分析或是分类;集成所有决策树为随机森林预测模型;向预测模型中输入测试集数据，通过取均值的方式，从所有决策树的预测结果生成随机森林的预测结果。

2 客运量预测方法

2.1 预测思路

水陆联运枢纽发展受诸多因素影响，单一方法的时间序列分析难以兼顾多种因素影响下的水陆联运枢纽客运量变化情况。随机森林算法在生成预测模型时，可同时处理大规模数据，且能够对初始数据集中的所有自变量输出特征变量的重要性进行分析。

利用随机森林算法优势，可尽可能多地选取与水陆联运枢纽客运量变化相关的特征变量作为随机森林预测模型的初始数据集;通过随机森林算法构建初始预测模型，选取特征变量重要性指标，对所有的特征变量进行重要性分析，筛选出的重要特征变量即代表了对水陆联运枢纽客运量影响较大的影响因素;依据特征变量重要性程度优选特征变量，形成预测数据集，以减小噪声与异常值对预测结果的影响，提升预测精度;基于预测数据集重新构建随机森林预测模型，并输入测试集对预测结果进行验证。

2.2 参数介绍

随机森林预测模型中包含森林规模（ntree）和基回归树预选的特征变量个数（mtry）两个参数，其中：ntree影响模型的泛化能力，决定了预测结果的方差;而mtry代表了树生长的深度，影响了单个回归树的拟合程度，决定了预测结果的偏差。与传统决策树不同，基回归树不需要剪枝，主要通过上述两个参数来控制随机森林预测模型的生成，合适的参数能使随机森林模型避免过拟合。通常运用袋外数据（OOB）估计对随机森林预测模型的参数进行优选。

OOB估计是在Bootstrap抽样的基础上，以OOB样本为验证集，计算袋外错误率（OOB error，Err）表示随机森林预测模型的泛化误差。OOB估计是随机森林泛化误差的一个无偏估计，其结果近似于需要大量计算的k折交叉验证。OOB估计过程如下：

假设数据集有S个样本，运用Bootstrap抽样在对数据集抽样时，总是存在一定比例的样本未被抽中，其中，比例P=（1 ）S，当S→+∞时，P收敛于0.368，该部分样本即为OOB样本。随机森林算法在预测客运量时，使用均差方来表示Err（E），公式如下：

式中： Nntree为森林规模; Nyear为子训练集的样本数; Ei为第i棵回归树的OOB估计值;yi为实际客运量; fOOB为使用OOB样本的估计值。

2.3 预测函数

基于变量重要性分析筛选出的特征变量构成新数据集，运用Bootstrap抽样，随机抽取P个样本、Q个特征变量，并重复以上操作K次，得到K个子训练集。对子训练集重新构建基回归树模型，并调整模型参数，便得到规模为K的回归随机森林。

集成随机森林所有回归树的预测结果，以均值的形式输出，即是通过随机森林预测的水陆联运枢纽客运量预测值。

式中： fK （x）为随机森林模型预测结果; fK （x，SK）为单棵回归树的预测结果;x为需要预测的节点，算例中指代需要预测的年份;SK为子训练集K。

2.4 重要性分析

为减少与枢纽客运量弱相关的特征变量对预测结果的影响，需要对初始数据集中的特征变量进行重要性分析，并筛选出符合预测精度要求的数据集。

随机森林算法在回归问题中处理重要性分析时，往往选用均方误差降低比例（%IncMSE， M）。 M是基于OOB估计，随机打乱一个特征变量值，重新计算新的E，然后计算模型准确度下降的百分比。第i个特征变量的重要性分析Mi计算式如下：

3 实例分析

3.1 获取变量

选取某水陆联运枢纽客运量相关数据，以客运量为目标变量，与目标变量相关的18个宏观性社会经济指标为自变量，部分变量见表1。选定2000―2019年作为研究区间，其中2000―2014年数据作为预测模型训练集，其余数据为预测模型测试集。

3.2 优选参数

参数优选是确定随机森林模型的前提，随机森林算法在作回归预测时，mtry值通常为自变量个数的1/3，应用到本算例中，初始数据集包含18个自变量，mtry数值宜取6，所以分别对mtry=5、mtry=6、 mtry=7进行OOB误差估计分析（见图2）。经随机森林模型验证，当mtry=6时，OOB误差估计值总体水平较低，且当ntree值趋于500时，OOB误差估计值最低且数值变化趋于稳定。由此为随机森林初始模型确定参数mtry=6，ntree=500。

3.3 特征变量重要性分析

根据Pi指标对初始数据集中每个特征变量进行重要性分析。为便于显示，将特征变量名称用字母代替，各个特征变量Mi值见图3。由图3分析结果显示，p（机场客运量）、m（城镇居民可支配收入）和j（旅游收入）对预测结果较为重要，b（高校在校生人数）和d（相邻水陆联运枢纽客运量）对预测结果影响较小，其余特征变量重要性程度一般。

将特征变量按照Mi降序排列，依次叠加选取的特征变量形成变量优选数据组D={（p），（p，m），…，（p，m，…，d）}，对每一个数据集参数优选，重复利用算法对D中各数据集进行准确度分析，最终得到不同特征变量组合的预测模型准确度。

由特征变量优选分析过程（见图4）得知：当变量数目在1～5时，随机森林预测模型准确度随着变量数目递增而显著提升;当变量数目为13时，即固定投资总额增加值纳入随机森林预测模型数据集，准确度达到最大值97.39%;当变量数目大于13时，准确度下跌，说明有4个特征变量对水陆联运枢纽客运量预测有干扰，应当删除以提升随机森林预测模型的准确度。因此，筛选出前13位特征变量作为预测数据集。

3.4 预测结果分析

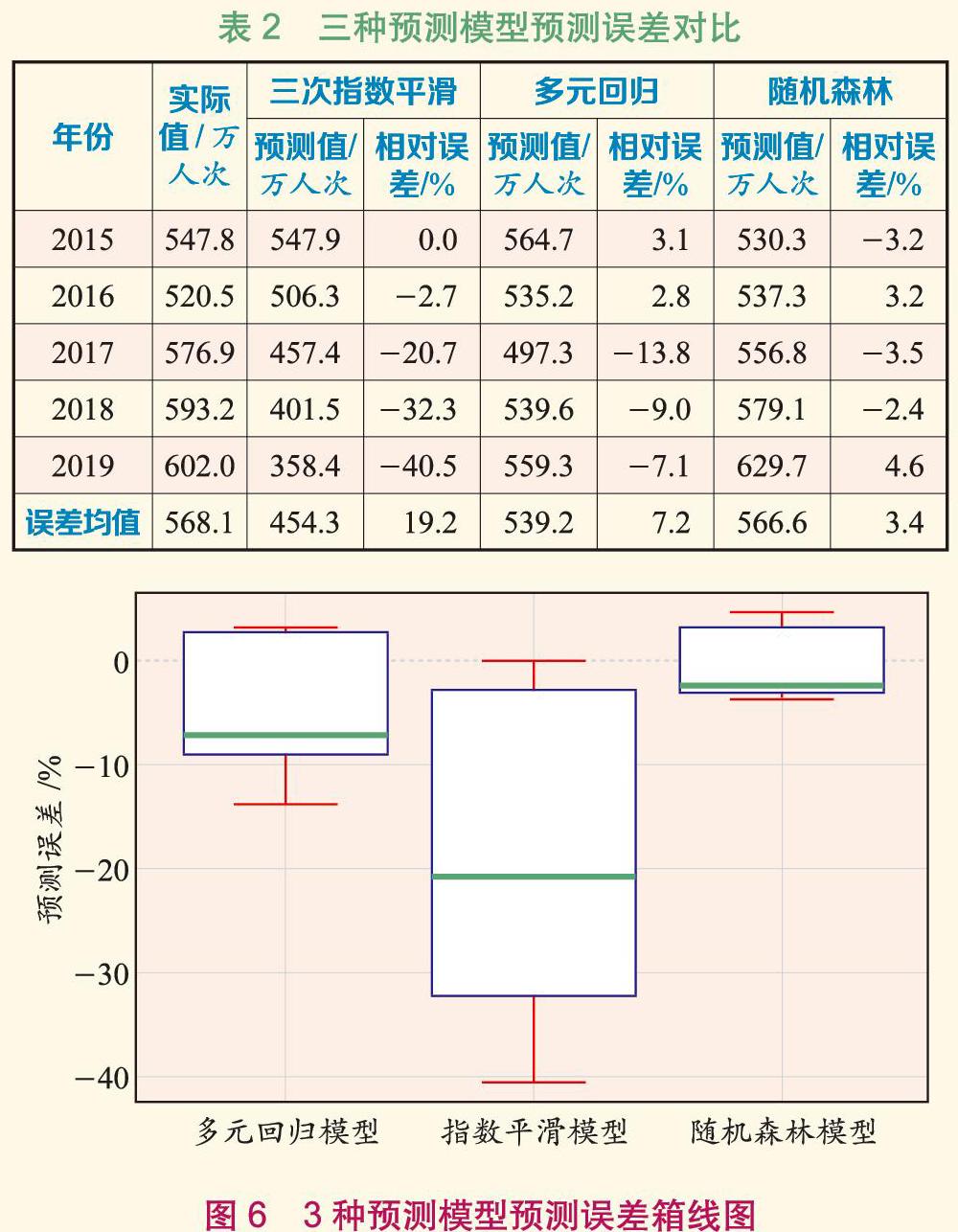
在特征變量优选的基础上，对新的数据集优选模型参数，利用随机森林模型预测2015―2019年某水陆联运枢纽客运量，并与三次指数平滑法和多元线性回归法的预测效果进行对比（见图5）。随机森林模型预测结果较其他两种预测方法的预测结果，与实际值偏差更小，总体更贴近实际值。

在3种预测模型的预测误差对比（见表2）的基础上绘制不同预测方法预测误差箱线图（见图6）。由图6可知：较三次指数平滑法与多元回归法，随机森林预测结果误差均值最小，且箱线图的中位数绝对值最小，体现随机森林预测结果总体较准确;随机森林预测结果的个体相对预测误差均在10%以内，表示随机森林模型对各年份的单点预测更接近实际值;随机森林的箱线图极值在可接受范围内，说明随机森林对异常值容忍性较好，误差波动较为稳定。

综上所述，随机森林预测模型较三次指数平滑法与多元回归法，在总体偏差、个体误差及误差波动水平方面表现较优。

4 结 语

水陆联运枢纽客运量往往受多种因素影响，算例以某水陆联运枢纽客运量为目标变量，选取多个与目标变量相关的因素作为预测的特征变量。通过随机森林算法重要性分析得出，机场客运量、城镇居民可支配收入及旅游收入3种特征变量与目标变量高度相关。

运用随机森林算法预测水陆联运枢纽客运量，不仅可以有效分析各影响因素对枢纽客运量的重要性程度，而且预测结果较为准确，可以作为水陆联运枢纽发展与改革的理论支撑，有助于枢纽经济更好更快地发展。