双边资金约束下基于公平偏好制造商的双渠道供应链融资策略
2021-10-10郭金森周永务任鸣鸣杨玉珍
郭金森 ,周永务 ,任鸣鸣 ,杨玉珍
(1.河南师范大学 商学院,河南 新乡 453007;2.华南理工大学 工商管理学院,广州 510640)
银行借贷与贸易信贷是供应链中资金约束企业最为常见的两种融资方式。当供应链上下游企业均存在资金约束时,可采用如下方法解决其资金不足问题:①“双边银行借贷”融资组合模式,即上游制造商和下游零售商均通过银行借贷来解决自身资金约束困境;②“银行借贷+贸易信贷”融资组合模式,即上游制造商通过银行借贷解决自身资金约束困境,并为下游订货资金不足的零售商提供贸易信贷契约,允许其将部分货款延期支付,进而解决零售商资金不足问题。然而,在不同的融资组合模式下,企业运营决策和收益可能发生不同的变化,并影响其对融资组合模式的选择偏好[1]。同时,行为研究表明,供应链成员通常具有公平偏好行为,他们同时关注自身与对方的利润高低,关心自身是否受到公平的待遇,进而导致企业运营及融资决策变得更加复杂[2-3]。随着电子商务的发展,很多制造商开始通过双渠道模式(线下实体零售商渠道+线上网络自营渠道)销售产品,例如惠普、三星、索尼等[4]。而双边资金约束环境下,上游双渠道制造商不仅要满足自身网络渠道产品需求,也要满足下游零售商实体渠道产品需求,加上消费者绿色环保意识的增强等,制造商扩大产品生产规模以及产品绿色化等活动将导致其更高的生产资金投入,进而需要向银行借贷更多资金并支付更多的借贷利息。因为制造商付出了大量的生产及融资成本,其在供应链利润分配过程中也往往更加注重利润分配的公平性,此时不同融资组合模式以及制造商公平偏好特性对双渠道供应链各主体运营决策及收益的影响也变得更加复杂,所以在双边资金约束环境下,研究带有公平偏好制造商的双渠道供应链融资策略具有重要意义。
目前关于供应链融资决策问题研究主要集中在单渠道供应链领域。在确定性需求环境下,Burkart等[5]研究指出,贸易信贷与银行借贷具有一定的互补性和替代性。之后,较多学者针对下游零售商存在资金约束的供应链,探讨了零售商银行借贷与贸易信贷融资模式选择策略[6-10]。李波等[11]进一步将上述研究拓展到零售商存在风险规避情形,探讨了其风险规避特性对各企业运作决策和融资模式选择策略的影响。针对上游制造商存在资金约束的供应链,王文利等[12]和占济舟等[13]探讨了制造商银行借贷与预付款融资模式选择策略。杨浩雄等[14]将上述研究拓展到绿色供应链中,探讨了制造商产品绿色指数对供应链运营决策及融资模式选择偏好的影响。上述研究都是考虑供应链中仅一方企业存在资金约束情况,金伟等[1]针对上下游企业均存在资金约束的供应链,建立了两种由交易信用与银行融资组合的融资模型,并分析了不同资金约束程度下,供应链上下游企业的融资决策。
上述研究主要基于单渠道供应链环境展开,而在双渠道环境下,张小娟等[15]探讨了资金约束零售商对贸易信贷和银行借贷两种融资模式的选择偏好。进一步,部分学者将上述问题拓展到仅零售商具有风险规避特性以及上下游企业均具有风险规避特性环境,研究企业风险规避行为对零售商融资策略选择的影响[16-17]。上述研究都假设下游零售商存在资金约束,肖肖等[18]探讨了当上游双渠道制造商存在资金约束时,其预付款融资与银行借贷融资策略选择问题。曹宗宏等[19]和郭金森等[3]针对资金约束的双渠道制造商可能存在风险规避/公平关切行为情形,探讨了上述行为特性对其融资策略选择的影响。
综上所述,目前供应链中关于企业融资决策问题的研究大多基于单渠道销售环境,而双渠道销售环境下企业融资决策问题研究还相对不足,且主要是针对供应链单边资金约束情形,假设仅上游/下游企业存在资金约束,未考虑上下游企业同时存在资金约束问题,更鲜有探讨双边资金约束下企业公平偏好特性对供应链融资策略的影响。因此,基于上述研究背景,本文针对上下游企业同时存在资金约束且制造商具有公平偏好特性的双渠道供应链,研究“双边银行借贷”以及“银行借贷+贸易信贷”两种不同融资组合模式下,供应链各主体最优运作策略和收益,并进一步讨论上下游企业初始资金规模、制造商公平偏好特性以及延期支付批发价敏感性等对供应链成员运营决策及收益的影响,最后分析不同市场条件下各主体对上述两种融资组合模式的选择偏好。
1 模型假设
针对同时存在资金约束的双渠道制造商和传统零售商组成的供应链,其中,制造商具有公平偏好特性,考虑采用如下方法解决供应链双边资金约束问题:①“双边银行借贷”融资组合模式,即上游制造商和下游零售商均通过银行借贷来解决自身资金约束困境;②“银行借贷+贸易信贷”融资组合模式,即上游制造商通过银行借贷解决自身资金约束困境,并为下游资金约束的零售商提供贸易信贷,允许其部分货款推迟支付。
在实践中存在较多规模庞大、实力雄厚的大型制造商(例如三星、海尔等),其往往是供应链中的领导者,有较强的定价和议价能力,而较多传统零售商通常规模较小、实力较弱,其产品定价等决策主要取决于制造商的决策。零售商通常在制造商批发价及网络渠道产品定价等决策后再进行自身产品价格决策,进而成为供应链中的追随者。因此,在供应链相关问题研究中,制造商为领导者而零售商为追随者的博弈模型假设被众多学者采用[3,18,20-24]。
本文假设双渠道供应链中,制造商处于核心地位,为供应链领导者,与零售商进行Stackelberg博弈。博弈顺序如下:制造商首先确定产品批发价和自身网络渠道产品直销价,而观察到制造商的决策后,零售商再确定自身实体渠道产品零售价。事件发生顺序如图1所示。
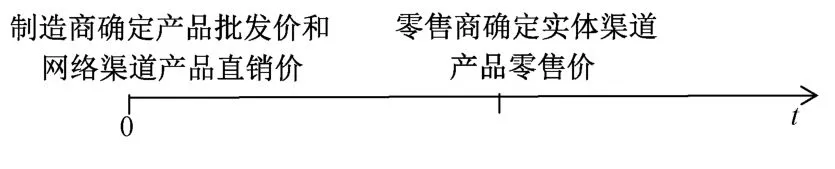
图1 双渠道供应链上下游企业决策顺序
参数说明:
a——市场潜在需求规模
φ——零售商实体渠道产品市场占有率,0<φ<1
p1——零售商实体渠道产品零售价
p2——制造商网络渠道产品直销价
θi(i=1,2)——对方渠道价格所引起的消费者转移程度,0<θi<1
w——制造商单位产品批发价
c——制造商单位产品生产成本
β——制造商公平偏好系数,0<β<1
γ——公平比例系数,γ>0
Bm——制造商初始资金规模
Br——零售商初始资金规模
Lm——制造商从银行借贷的资金规模
Lr——零售商从银行借贷的资金规模
rb1——银行为零售商提供的贷款利率
rb2——银行为制造商提供的贷款利率
k——制造商延期支付批发价敏感系数,k>0
2 基本模型建立
首先给出无资金约束情形,双渠道供应链各主体最优运营决策和收益。参考文献[25-26],得到零售商实体渠道和制造商网络渠道的需求分别为:
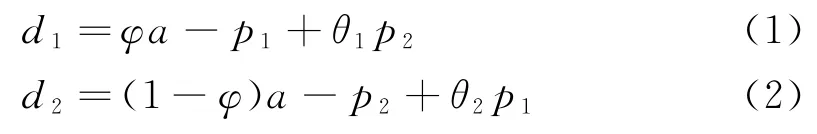
为了计算方便,且不影响本文相关结论,参考文献[25-26],令θ1=θ2=θ,可得制造商无公平偏好特性下,零售商和制造商收益函数分别为:
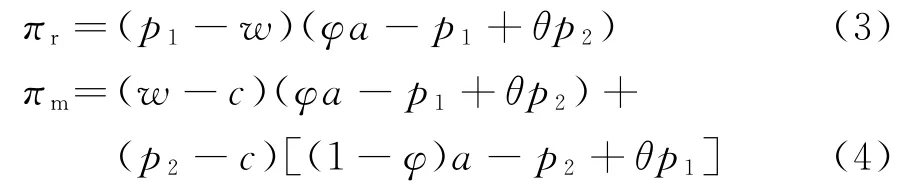
参考文献[27-28],当制造商存在公平偏好时,其效用函数为:um=πm-β(γπr-πm)。本文公平参考点为参与方的相对利润,并假设当己方利润低于对方相对利润时,公平效用为负值;否则,将获得正的公平效用。因此,可得双渠道制造商存在公平偏好时,其效用函数为
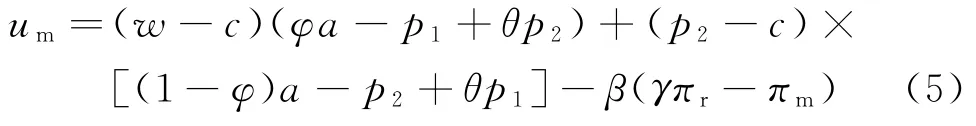
采用逆推法,并记上标0为双渠道供应链上下游企业均无资金约束情形。由式(3)可得制造商决策给定时,零售商收益函数是关于p1的凹函数,从而有
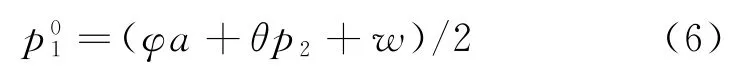
将式(6)代入式(5),易得公平偏好的双渠道制造商效用函数为
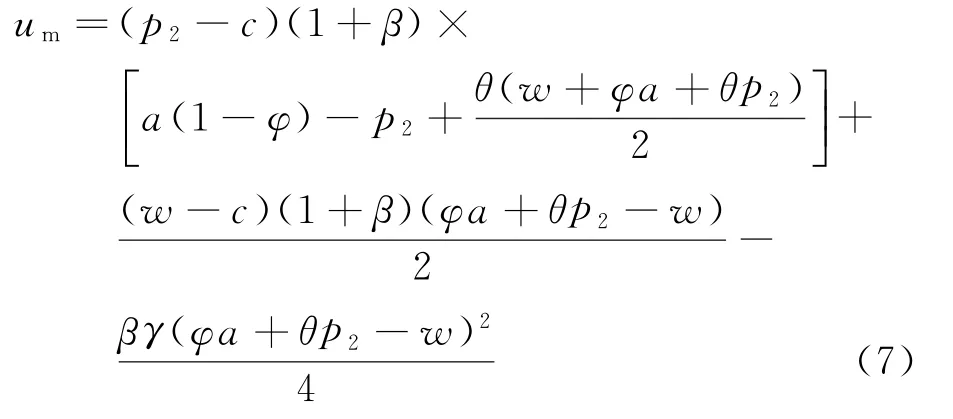
由式(7)易得制造商效用函数um是关于(p2,w)的联合凹函数,可得定理1。
定理1无资金约束下,双渠道制造商与传统零售商的最优定价决策分别为:
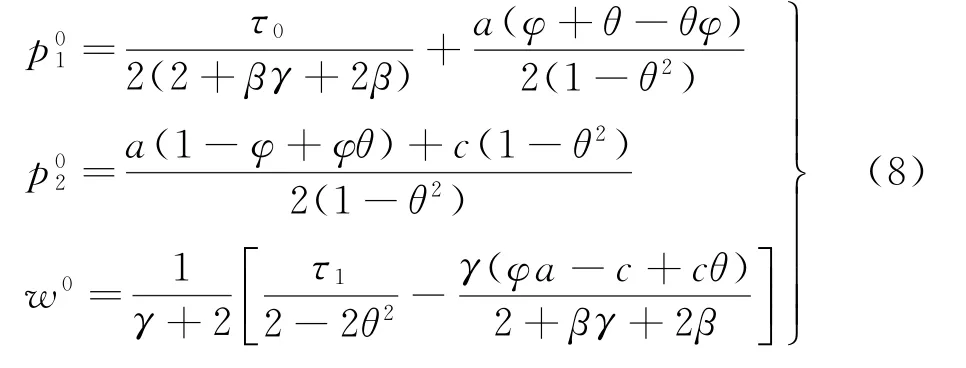
从而易得供应链各主体的需求和收益分别为:
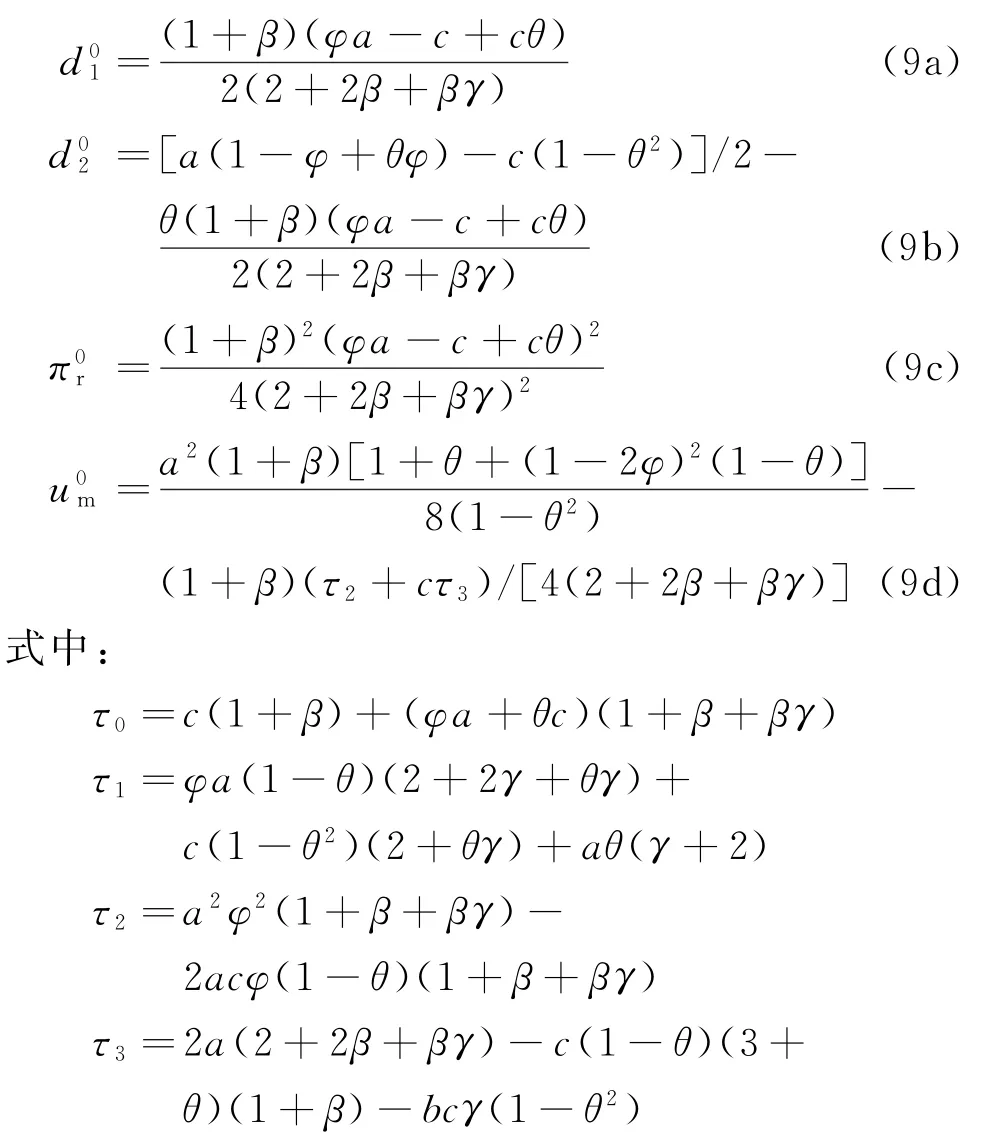
分析无资金约束情形下,制造商公平偏好程度对双渠道供应链运营决策和收益的影响,可得性质1。
性质1
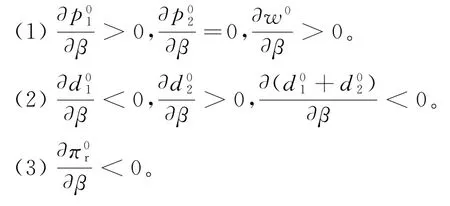
由性质1易得无资金约束下,制造商公平偏好特性不影响其网络渠道产品直销价,但会导致批发价和零售商产品零售价的提高。即公平偏好的制造商会通过提高产品批发价的形式从零售商处分割更多的单位产品批发收益,而零售商只能通过提高其产品零售价的方式将增加的单位产品批发价成本转嫁给下游消费者,由消费者买单。因为零售商渠道产品售价提高,而制造商网络渠道产品售价不变,零售商渠道部分消费者需求转移到制造商网络渠道上,导致零售商渠道需求减少,制造商网络渠道需求增加。而供应链中产品整体售价的相对提高,导致下游消费者需求被削弱,双渠道供应链总体需求规模下降。最后,由性质1(3)可知,零售商收益随着制造商公平偏好程度的增大而减少,即存在公平偏好的双渠道制造商会通过分割零售商更多收益的方式来降低自身不公平感受。
结论1供应链无资金约束时,零售商偏爱与无公平偏好的上游双渠道制造商合作。
结论1指出了无资金约束下,供应链中零售商对双渠道制造商的选择偏好。然而,在实践中,上下游企业都可能面临资金不足困境。下面将进一步探讨供应链存在双边资金约束时,在两种不同的融资组合模式下(“双边银行借贷”和“银行借贷+贸易信贷”)各企业最优运营决策与收益。
3 双边资金约束下,供应链“银行借贷+贸易信贷”融资组合模式
考虑双边资金约束情形,供应链采用“银行借贷+贸易信贷”融资组合模式来解决链条资金约束困境。此模式下,制造商通过银行借贷解决自身资金约束困境,并为零售商提供贸易信贷合同,允许零售商部分货款推迟支付,以解决零售商订货资金不足问题。设资金约束的制造商和零售商的初始资金规模分别为Bm和Br,易得制造商从银行借贷金额为:Lm=c(d1+d2)-Bm。设银行为制造商提供的借贷利率为rb2,则制造商需向银行支付的借贷利息为Lmrb2。为激励资金不足的零售商先用其全部初始资金Br支付部分产品货款,制造商对零售商推迟支付的产品将设置一个新的相对较高的批发价格w1=wek(k>0),其中,k为制造商延期支付批发价敏感系数,k越大,零售商需支付给制造商的延期支付产品批发价越高[16]。
从而易得零售商和双渠道制造商的收益函数分别为:
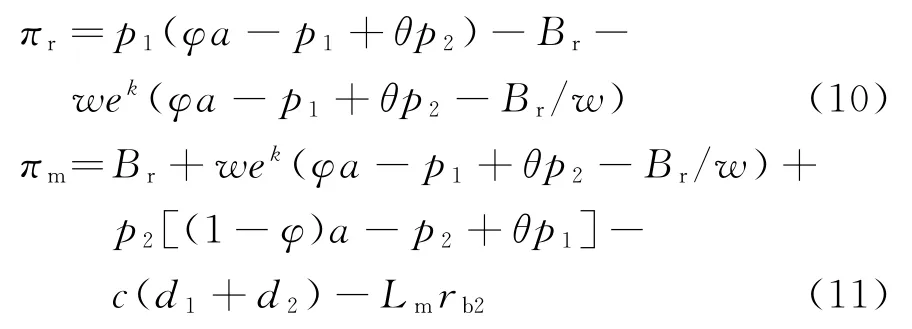
可得双渠道制造商存在公平偏好时,其效用函数为
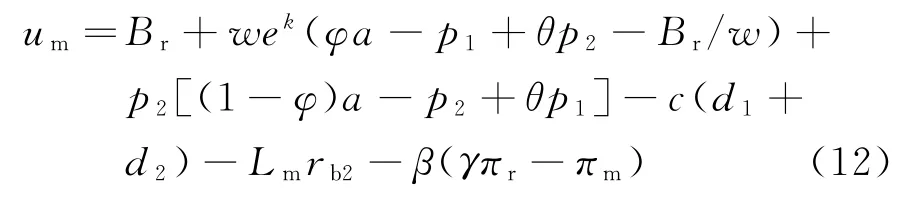
记上标1为双边资金约束情形下供应链采用“银行借贷+贸易信贷”融资组合模式。仍然采用逆推法,首先考虑当制造商批发价与网络渠道直销价给定时,零售商的最优渠道产品定价决策。
3.1 零售商最优决策
由式(10)易得零售商收益函数是关于其产品定价p1的凹函数,从而有
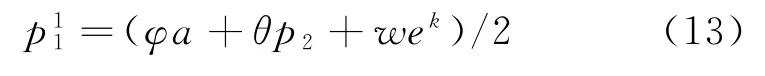
3.2 制造商最优策略
将式(13)代入式(12),可得公平偏好的双渠道制造商效用函数转化为
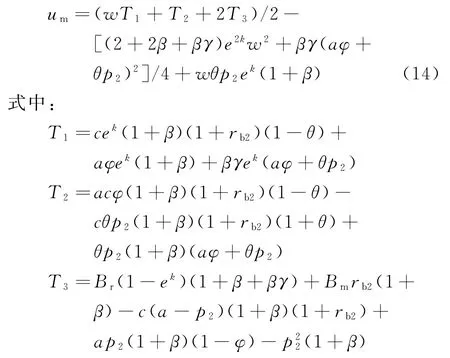
由式(14)易得公平偏好的双渠道制造商效用函数um是关于(p2,w)的联合凹函数,可得定理2。
定理2“银行借贷+贸易信贷”融资组合模式下,双渠道制造商与传统零售商的最优定价决策分别为:
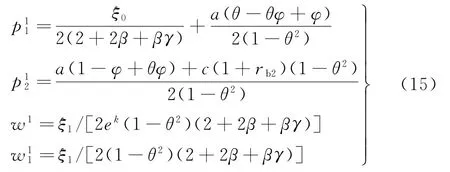
从而易得零售商和双渠道制造商的需求和收益分别为:

式中:
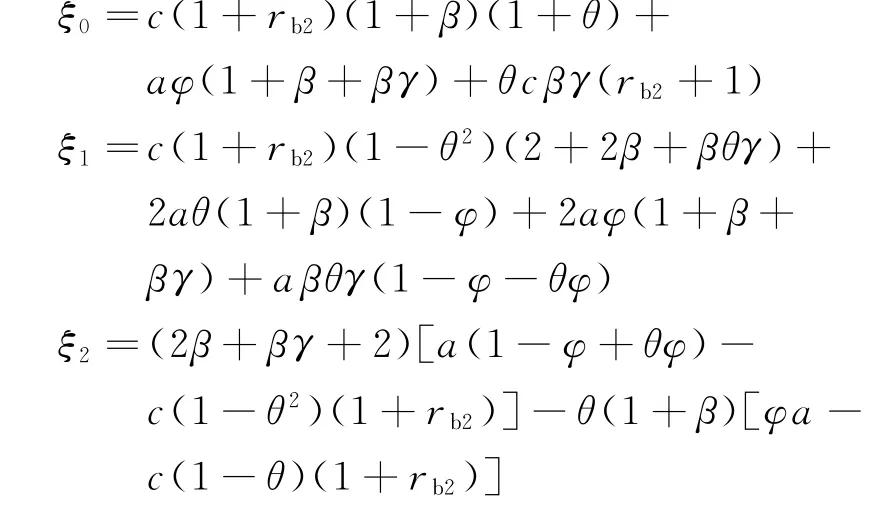
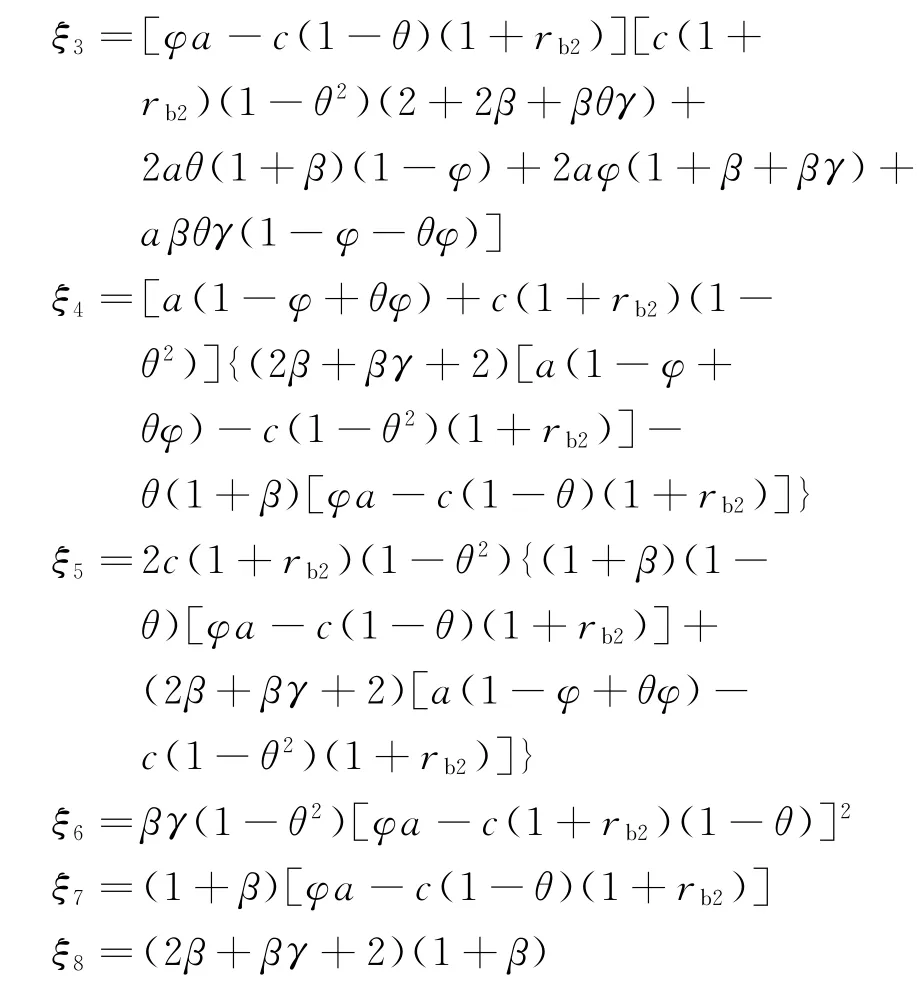
下面分析在此模式下,制造商公平偏好程度对各主体运营决策和收益的影响,可得性质2。
性质2
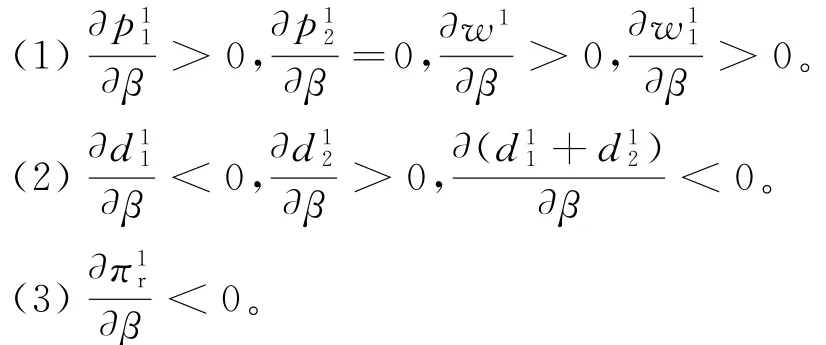
由性质2可得双边资金约束下,供应链采用“银行借贷+贸易信贷”融资组合模式时,制造商公平偏好程度对双渠道供应链运营决策与收益的影响与无资金约束情形类似,这里不再赘述。
结论2双边资金约束下,供应链采用“银行借贷+贸易信贷”融资组合模式时,零售商仍偏爱与无公平偏好的双渠道制造商合作。
下面进一步分析在此模式下,企业初始资金规模对各主体运营决策和收益的影响,可得性质3。
性质3
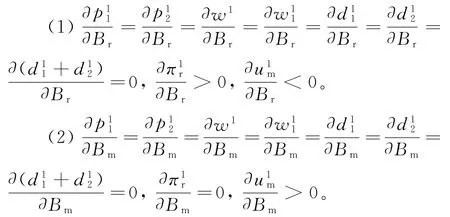
由性质3可得“银行借贷+贸易信贷”融资组合模式下,上下游企业初始资金规模不影响各主体最优运营决策和需求,但对各主体收益产生影响。随着零售商初始资金规模的增加,零售商资金约束困境减弱,需要推迟支付给制造商的货物量减少,节约了一定量的延期支付货款成本(延期支付批发价高于正常支付批发价),从而实现了零售商收益的不断增加。此时,制造商通过延期支付合同获取较高批发价及批发收益的能力减弱,制造商总收益不断减少。进一步,随着制造商初始资金规模的增加,制造商资金约束困境减弱,其对金融机构的资金借贷规模减少,需要支付的借贷利息额下降,进而实现制造商收益的不断增加。而此时零售商对延期支付合同的依赖程度没有变化,零售商收益保持不变。
与供应链无资金约束情形对比,可得结论3。
结论3

证明见附录。
由结论3易得双边资金约束下,供应链采用“银行借贷+贸易信贷”融资组合模式时,制造商提供给零售商的延期支付批发价始终高于无资金约束时其正常批发价。此时,制造商将自身的银行借贷融资成本部分转嫁给了进行延期支付融资的下游零售商。在此模式下,制造商提供给零售商的正常批发价不一定高于无资金约束时其正常批发价。当银行借贷利率较低时,制造商提供的正常批发价低于无资金约束时的正常批发价,此时为激励零售商将所有初始资金进行正常订货,其给予了零售商一定的批发价优惠,制造商银行借贷融资成本主要通过提高延期支付批发价来弥补;当银行借贷利率较高时,制造商融资成本较高,其提供的正常批发价高于无资金约束时的正常批发价,此时制造商通过两个阶段批发价的提高(正常批发价和延期支付批发价),将部分融资成本转嫁给了下游零售商。由于供应链各主体均付出了相应的融资成本,零售商实体渠道和制造商网络渠道的产品售价均高于无资金约束时其产品售价,导致双渠道需求均低于无资金约束时各渠道需求。
进一步,双边资金约束下,“银行借贷+贸易信贷”融资组合模式有效解决了零售商资金约束困境,尽管零售商渠道需求有所下降,但零售商渠道单位产品售价提高,从而零售商收益并非始终低于其无资金约束时的收益。当市场潜在需求规模较低时,零售商始终获得高于其无资金约束时所得收益;当市场潜在需求规模较高时,制造商相对较低的借贷利率可以降低零售商批发价成本支出,仍然能使零售商获得高于其无资金约束时所得收益;否则,零售商将获得低于其无资金约束时的收益。
4 双边资金约束下,供应链“双边银行借贷”融资组合模式
考虑双边资金约束情形,供应链采用“双边银行借贷”融资组合模式来解决链条资金约束困境。在此模式下,制造商和零售商均通过银行借贷解决自身资金约束困境,易得双渠道制造商和传统零售商从银行借贷的金额分别为:Lm=c(d1+d2)-Bm,Lr=wd1-Br。由于制造商和零售商属于不同的企业主体,其企业规模、负债水平、信用等级等可能有所不同,银行为其提供的贷款利率也会有所差别,故分别用rb1和rb2表示银行为零售商和制造商提供的贷款利率,当制造商和零售商的信用等级等条件基本一致时,银行将为他们提供相同的贷款利率(即rb1=rb2);否则,银行为双方提供不同的贷款利率(即rb1≠rb2)。进一步,可得零售商和制造商需要向银行支付的借贷利息(即银行的收益)分别为Lrrb1和Lmrb2。
从而易得零售商和双渠道制造商的收益函数分别为:
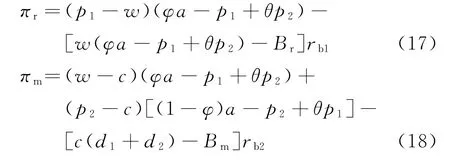
可得公平偏好的双渠道制造商效用函数为
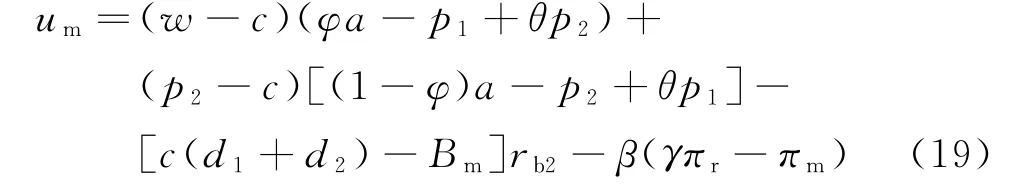
记上标A 为双边资金约束情形下供应链采用“双边银行借贷”融资组合模式。采用逆推法,首先考虑当双渠道制造商产品批发价与自身网络渠道产品定价决策给定时,零售商的最优渠道产品定价决策。
4.1 零售商最优决策
由式(17)易得零售商收益函数是关于其产品定价p1的凹函数:
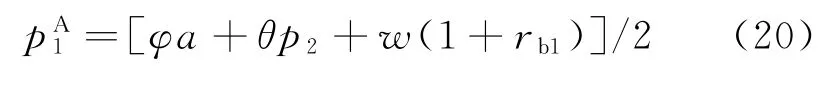
4.2 制造商最优决策
将式(20)代入式(19),易得公平偏好的双渠道制造商的效用函数转化为
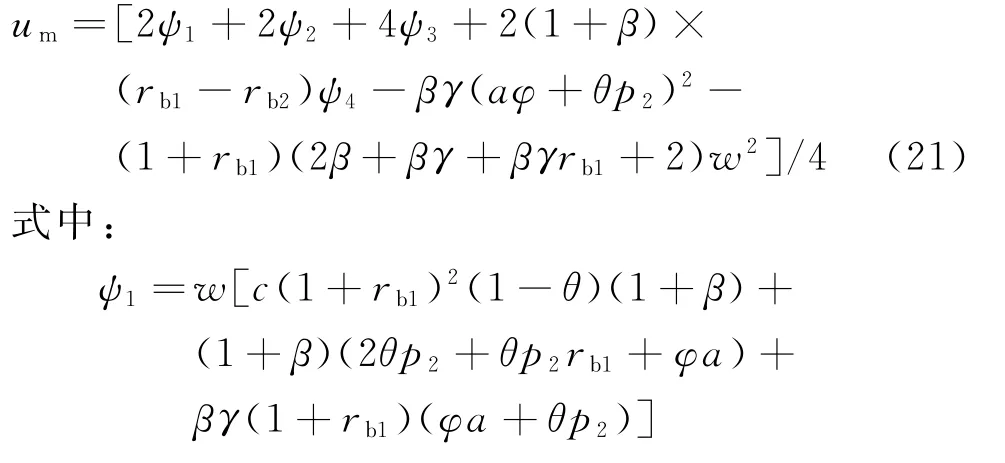
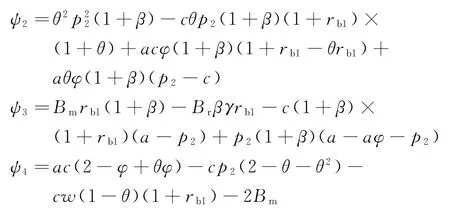
由式(21)可得制造商效用函数um关于(p2,w)的海塞矩阵为
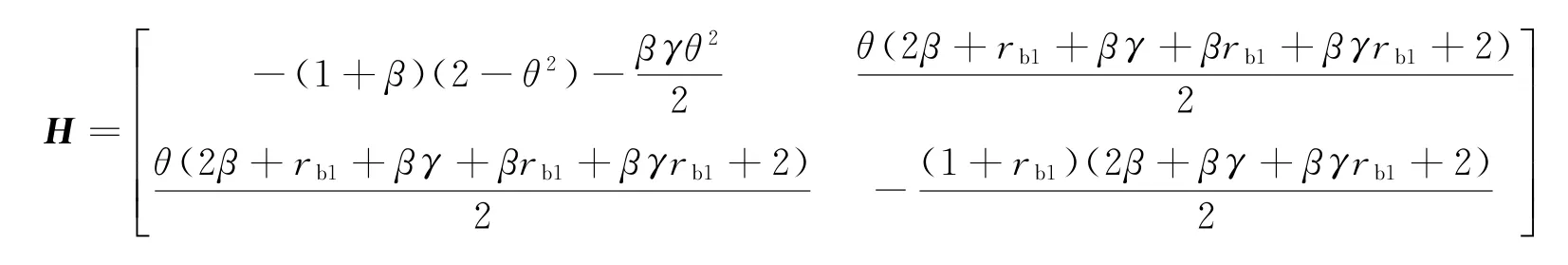
其中,
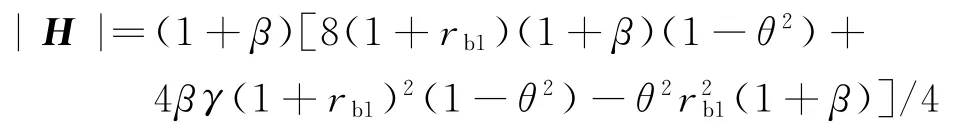
可得性质4。
性质4“双边银行借贷”融资组合模式下,公平偏好的双渠道制造商效用函数um分别是p2和w的凹函数,但不是(p2,w)的联合凹函数。
由性质4 可得制造商效用函数并非始终是(p2,w)的联合凹函数。下面分两种情形讨论。
情形1当|H|>0时,制造商效用函数um关于(p2,w)的海塞矩阵为负定,即um是关于(p2,w)的联合凹函数,此时有
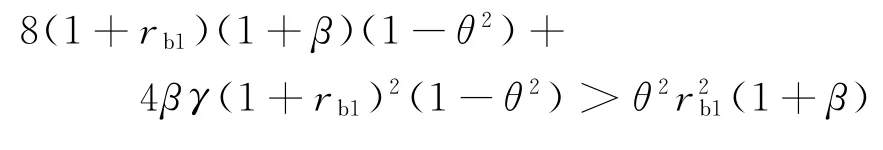
仍然采用逆推法分析,可得定理3。
定理3“双边银行借贷”融资组合模式下(情形1),双渠道制造商与传统零售商的最优定价决策分别为:
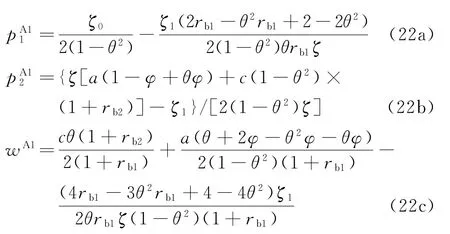
从而易得供应链各主体的需求和收益分别为:
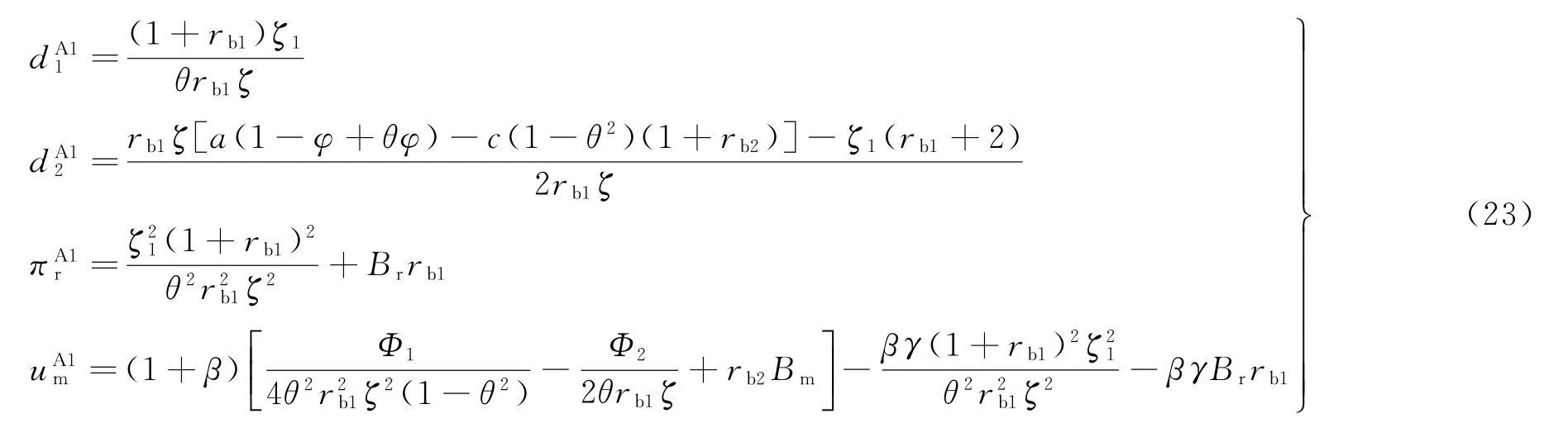
式中:

“双边银行借贷”融资组合模式下,银行通过向零售商和制造商借贷可获得的收益分别为Lrrb1和Lmrb2。从而,由定理3可得银行通过给零售商和制造商提供借贷服务所得收益分别为:
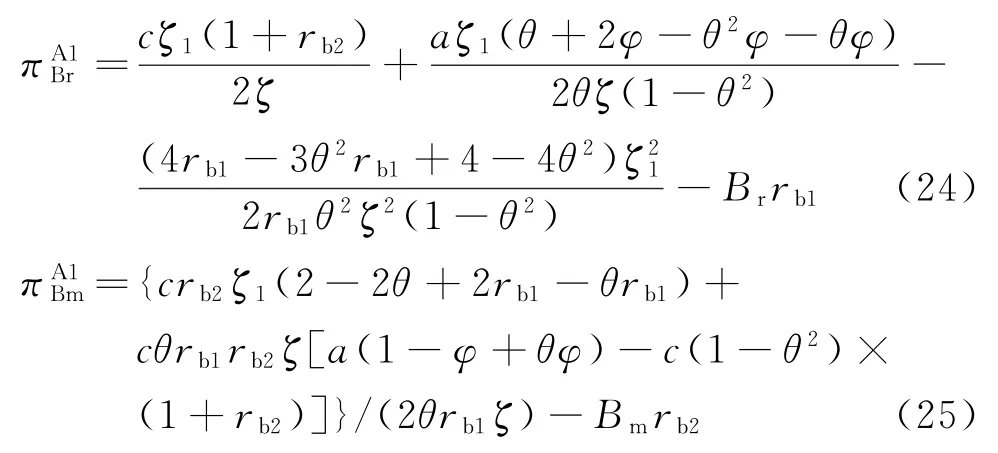
结论4当Br<B*r时,银行偏爱为下游零售商提供贷款融资服务;否则,其将更加偏爱为上游制造商提供贷款融资服务。
证明见附录。
下面分析在此情形下,企业初始资金规模对各主体运营决策和收益的影响,可得性质5。
性质5

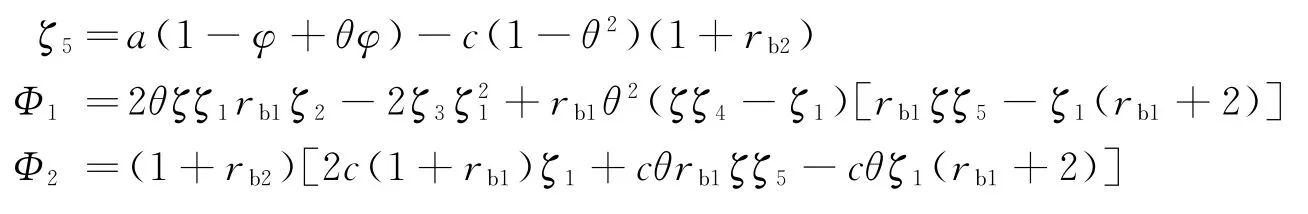
由性质5可得与“银行借贷+贸易信贷”融资组合模式类似,在此模式下,企业初始资金规模不影响各主体最优运营决策和需求,但对各主体收益产生重要影响。随着零售商初始资金规模的增加,零售商资金约束情况减弱,从银行借贷金额减少,借贷利息下降,零售商收益逐渐增加。由于制造商存在公平偏好特性,此时零售商收益的增加给制造商带来收益分配不公平的负效应,制造商效用下降。进一步,随着制造商初始资金规模的增加,制造商资金约束情况减弱,从银行借贷金额减少,借贷利息下降,制造商收益逐渐增加。因为供应链中无内部贸易信贷契约的影响,所以零售商的收益与制造商初始资金规模的大小无关。
情形2当|H|≤0时,制造商效用函数um不是(p2,w)的联合凹函数。运用两阶段优化技术,在制造商网络渠道产品定价p2给定下,首先寻找到最优的批发价w,代入制造商效用函数um,得到仅关于网络渠道产品定价p2的制造商效用函数,然后寻找最优的p2来最大化制造商效用。
由式(21)可得对任意给定的网络渠道产品定价p2,制造商最优产品批发价为
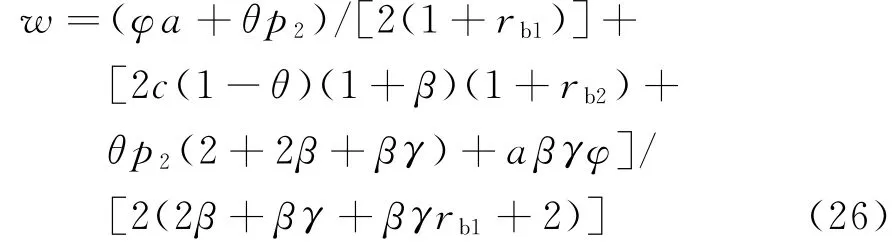
将式(26)代入式(21),易得公平偏好的双渠道制造商效用函数转化为
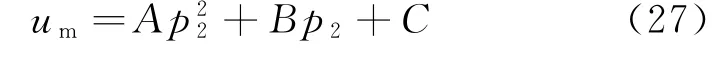
式中:
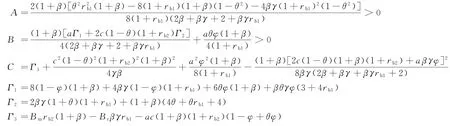
从而易得公平偏好的双渠道制造商效用um关于其网络渠道产品定价p2始终单调递增,但因双渠道需求不能为负,即满足d1≥0,d2≥0,所以可得定理4。
定理4“双边银行借贷”融资组合模式下(情形2),双渠道供应链各主体最优决策和需求分别为:
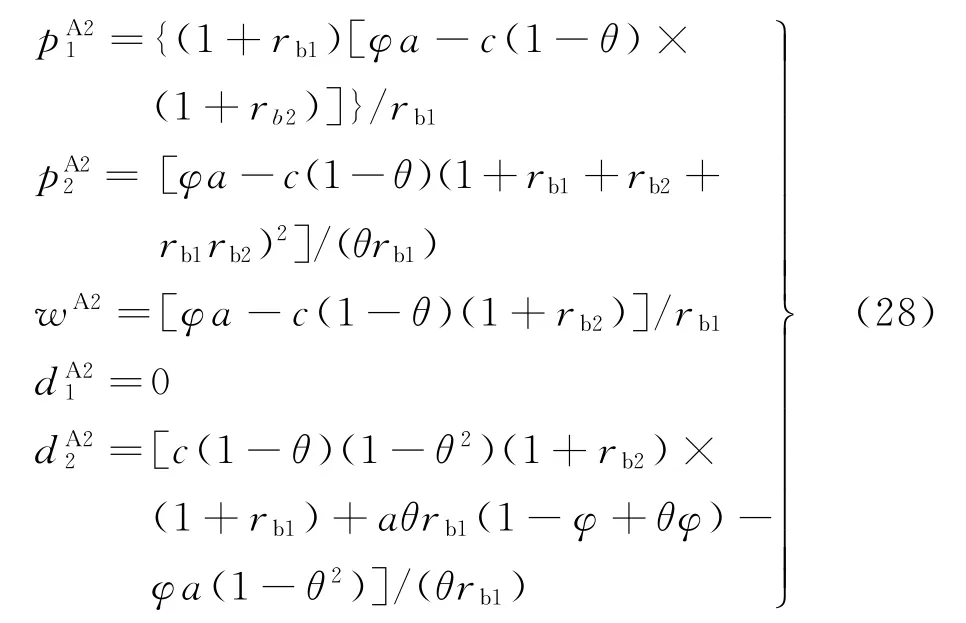
由定理4可得在此情形下,零售商实体渠道需求为零,其无法再通过销售产品获得收益。因此,零售商会放弃选择银行借贷融资模式,此时制造商将有充分动机通过为零售商提供贸易信贷契约来解决零售商订货资金不足困境,更好地满足零售商订货需求,以获得更多的批发收益。
对比两种不同融资组合模式下零售商和制造商的收益,分析各主体对不同融资组合模式的选择偏好,可得定理5。
定理5
(1)当k>k1时,有;否则
(2)当k<k2时,有否则
证明见附录。
由定理5可得双边资金约束下,供应链各主体对两种不同融资组合模式的选择偏好与制造商延期支付批发价敏感性密切相关。当制造商延期支付批发价敏感性较低时,零售商在“双边银行借贷”融资组合模式下所得收益高于其在“银行借贷+贸易信贷”融资组合模式下所得收益。此时,零售商将偏爱选择“双边银行借贷”融资组合模式。对制造商而言,当其对延期支付批发价敏感性较低时,其更加偏爱选择“银行借贷+贸易信贷”融资组合模式。
5 数值分析
前面模型分别给出了无资金约束以及双边资金约束时“银行借贷+贸易信贷”和“双边银行借贷”融资组合模式下企业最优决策。下面将通过数值例子来验证本文有关结论,并分析制造商公平偏好、银行贷款利率以及制造商延期支付批发价敏感性等对各主体运营决策及收益的影响。
例1制造商公平偏好程度对供应链的影响。参考中国人民银行授权全国银行间同业拆借中心公布的数据,2020年7月贷款市场报价利率:1年期为3.85%,5年期以上为4.65%。假设银行提供给零售商和制造商的贷款利率分别为:rb1=0.05,rb2=0.04。其他模型参数设置为:a=100,c=15,θ=0.3,φ=0.6,k=0.2,γ=0.8。
由图2、3可得无资金约束以及双边资金约束时“银行借贷+贸易信贷”融资组合模式下,制造商公平偏好特性对上下游企业运营决策和需求的影响规律与性质1和性质2一致,这里不再赘述。由图4可得“双边银行借贷”融资组合模式下,随着制造商公平偏好程度的增大,双渠道产品售价均提高,且零售商实体渠道产品售价提高程度高于制造商网络渠道。此时,零售商实体渠道需求逐渐下降,而制造商网络渠道需求逐渐增加。进一步,由图2~4可得在不同情形下,制造商公平偏好特性对其自身以及供应链总收益产生积极影响,制造商通过产品批发价和网络直销价格的设计,有效增加了自身收益,但却可能损害零售商收益。随着制造商公平偏好程度的增大,零售商收益逐渐减少。
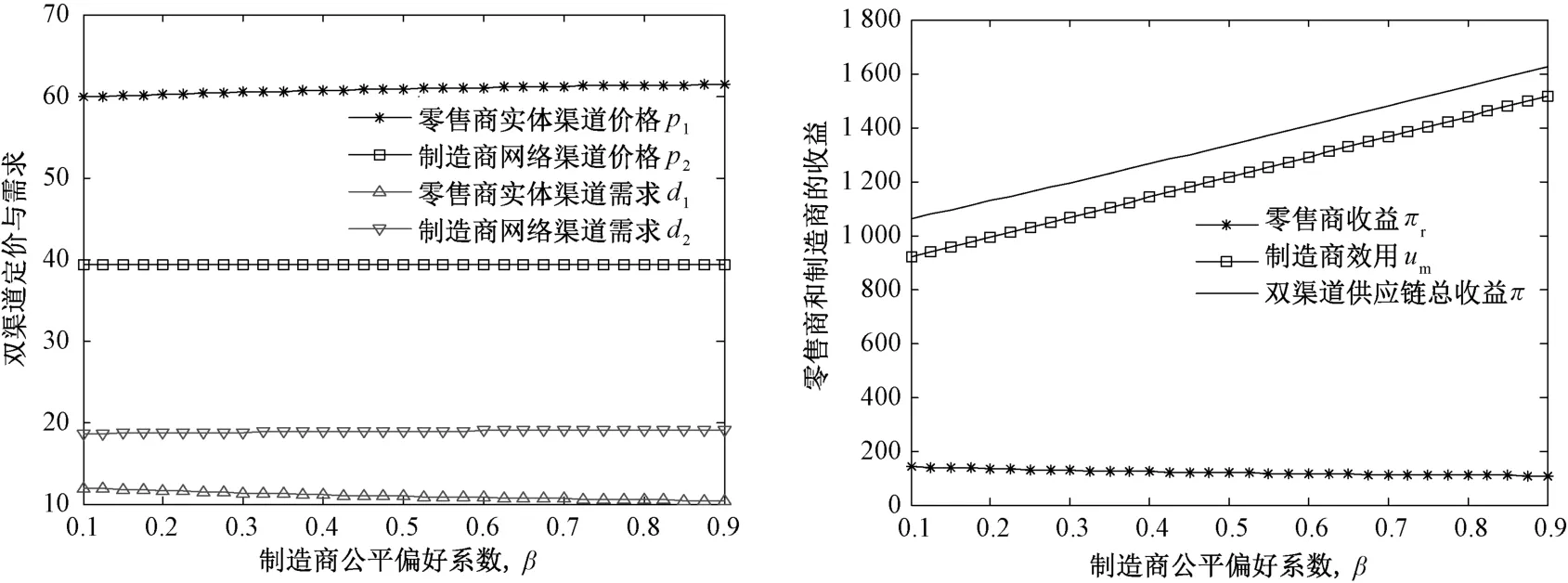
图2 无资金约束情形下,制造商公平偏好对博弈均衡的影响
图3 双边资金约束时“银行借贷+贸易信贷”融资组合模式下,制造商公平偏好对博弈均衡的影响(Br=180,Bm=200)
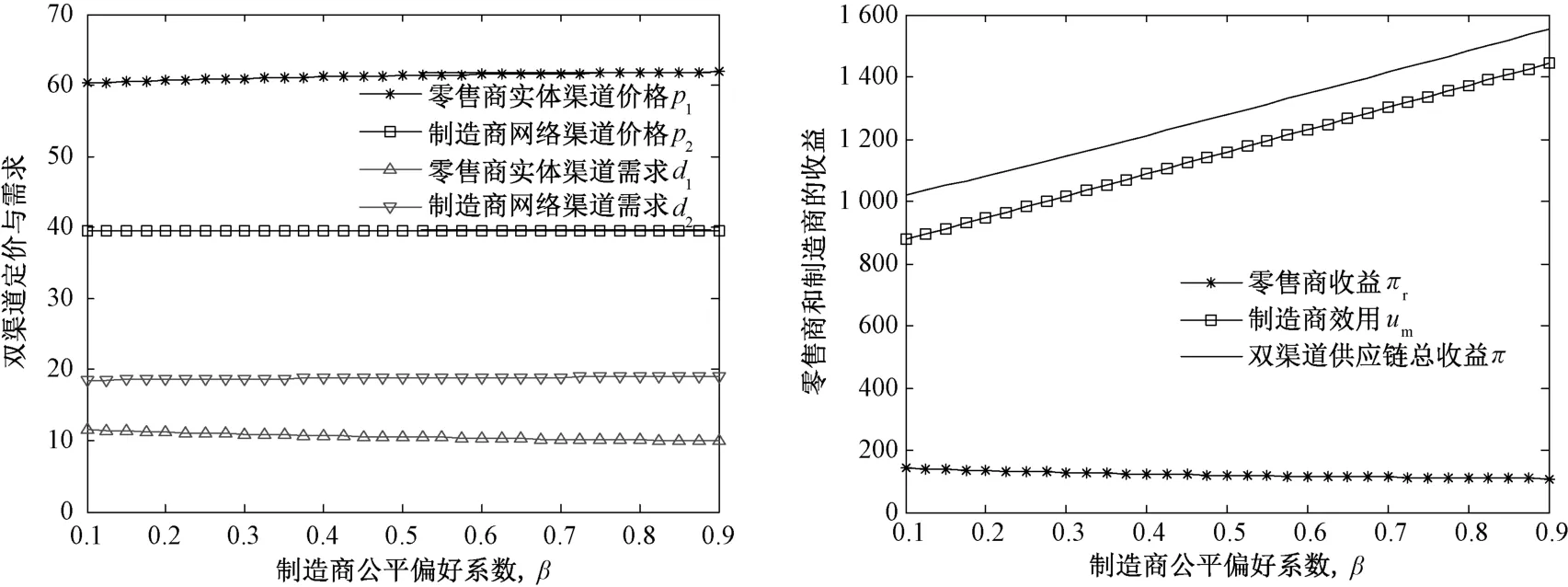
图4 双边资金约束时“双边银行借贷”融资组合模式下,制造商公平偏好对博弈均衡的影响(Br=180,Bm=200)
例2上下游企业贷款利率的差异对供应链的影响。模型参数设置为:Br=190,Bm=200,a=100,c=15,θ=0.3,φ=0.6,rb1=0.05,γ=0.8,β=0.5,k=0.2。
由表1可得在两种不同的融资组合模式下,相对于零售商贷款利率,当制造商贷款利率逐渐提高时,制造商融资成本增加,其网络渠道产品定价逐渐提高,制造商将增加的融资成本转嫁给下游消费者,网络渠道消费者需求逐渐下降。作为供应链跟随者,零售商实体渠道产品定价也逐渐提高,实体渠道消费者需求逐渐下降。随着制造商贷款利率的提高,制造商和零售商的收益均不断下降,即银行对制造商借贷利率的提高对供应链各主体收益产生消极影响。
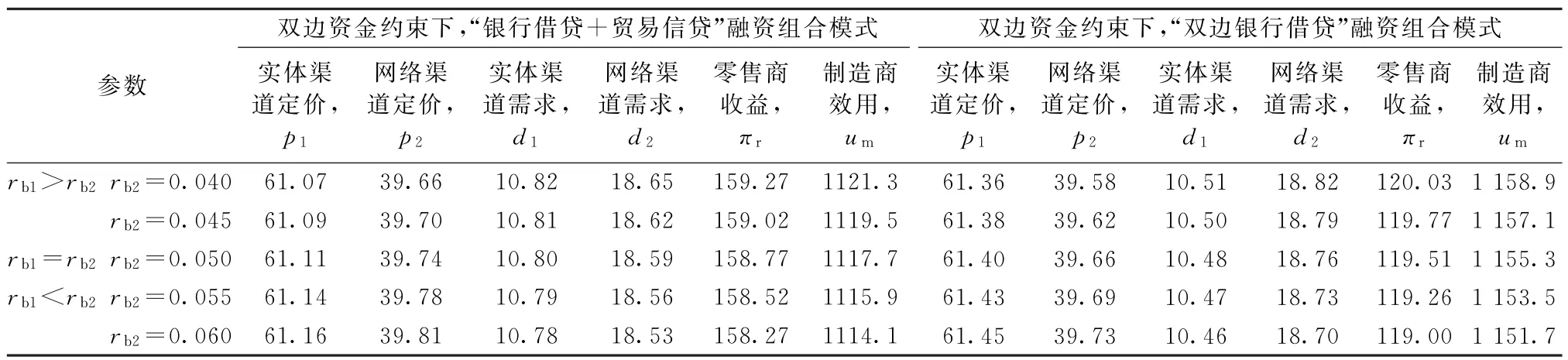
表1 不同融资模式下,供应链各主体运营决策及收益
例3在不同融资模式下,制造商延期支付批发价敏感系数不断变化时,零售商、制造商以及供应链总收益的变化,分析各主体对不同融资组合模式的选择偏好。模型参数设置为:Br=190,Bm=200,a=100,c=15,θ=0.3,φ=0.6,rb1=0.05,rb2=0.04,γ=0.8,β=0.5。
由表2可得在两种不同的融资组合模式下,资金约束的零售商均可能获得高于其无资金约束时所得收益,即适度的资金约束情况对零售商可能是有益的。而双渠道制造商的收益通常低于其无资金约束时所得收益。
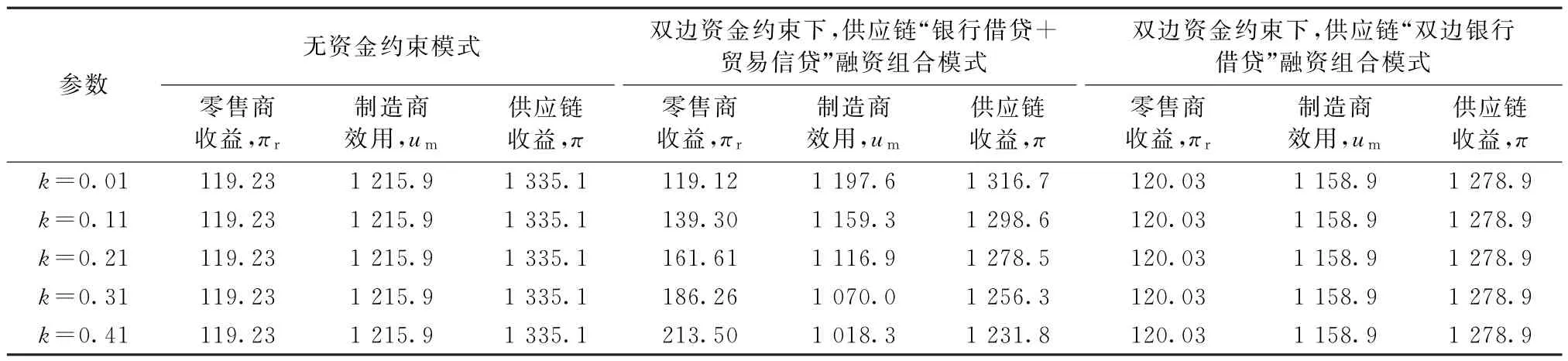
表2 不同融资模式下,供应链各主体收益以及总收益
进一步,双边资金约束下,当制造商延期支付批发价敏感性相对较低时(k≤0.01),零售商在“银行借贷+贸易信贷”融资组合模式下所得收益低于其在“双边银行借贷”融资组合模式下所得收益,此时零售商偏爱选择“双边银行借贷”融资组合模式;否则,其将更加偏爱选择“银行借贷+贸易信贷”融资组合模式。对制造商而言,当其延期支付批发价敏感性相对较低时(k≤0.11),其偏爱选择“银行借贷+贸易信贷”融资组合模式;否则,其将更加偏爱选择“双边银行借贷”融资组合模式。对整个供应链而言,当制造商延期支付批发价敏感性相对较低时(k≤0.11),“银行借贷+贸易信贷”融资组合模式要优于“双边银行借贷”融资组合模式;否则,“双边银行借贷”融资组合模式对整个供应链而言是占优的。
6 结论
针对存在双边资金约束的双渠道供应链,本文建立了“双边银行借贷”以及“银行借贷+贸易信贷”两种不同融资组合模式下的供应链融资决策模型,分析了企业初始资金规模、制造商公平偏好特性以及延期支付批发价敏感性等对各成员决策及收益的影响。研究发现,供应链融资组合模式不仅有效解决了各主体资金约束困境,且零售商可能获得高于其无资金约束时所得收益。通过对比两种不同融资组合模式下各主体收益,发现当制造商延期支付批发价敏感性较低时,零售商偏爱选择“双边银行借贷”融资组合模式;否则,其将偏爱“银行借贷+贸易信贷”融资组合模式。对制造商而言,当其延期支付批发价敏感性较低时,其偏爱选择“银行借贷+贸易信贷”融资组合模式;否则,“双边银行借贷”融资组合模式占优。
附录
结论3的证明
(1)由式(8)、(15)可得

结论4的证明
由式(24)、(25)可得当Br<时,恒有>0,此时银行通过给零售商提供借贷服务能获得较高的利息收入;否则,银行通过给制造商提供借贷服务能获得更高的利息收入。其中:
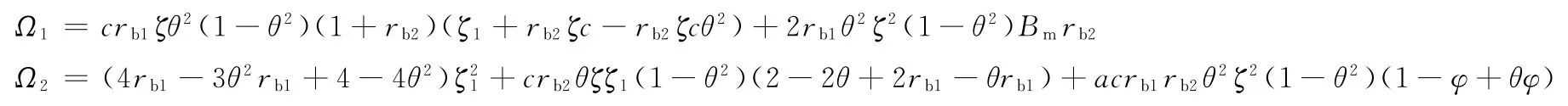
定理5的证明

