高燃耗陶瓷燃料颗粒的参数化建模及强度分析
2021-10-09吕俊男
杨 烁,吕俊男,李 群,*
(1.西安交通大学 航天航空学院 机械结构强度与振动国家重点实验室,陕西 西安 710049; 2.中国核动力研究设计院 反应堆燃料及材料重点实验室,四川 成都 610213)
弥散型燃料元件[1-2]是将易裂变燃料相以小颗粒的形式均匀弥散在相对惰性的非裂变材料基体中的一种混合物核燃料。由于燃料颗粒被基体材料分隔开,使裂变产物损伤局限在燃料颗粒及其周围基体内,不受裂变产物损伤的基体能形成连续网络,这样有利于包容裂变产物、抑制燃料肿胀,且燃料元件芯部温度低,导热性好,从而允许燃料达到更高的燃耗和安全可靠性,因此被广泛用于研究试验堆和动力堆[3]。
相对于普通的颗粒增强复合材料,弥散燃料的特殊性在于中子辐照条件下,核燃料颗粒内的易裂变物质,如铀会发生裂变和嬗变,此过程中产生的裂变气体不断聚集形成气泡,并导致燃料颗粒辐照肿胀[2]。高燃耗状态下,气体肿胀致使燃料颗粒逐渐演变成多孔结构,颗粒内气孔的尺寸和位置的非均匀分布与孔间的应力干涉效应极易导致气孔开裂贯通。事故工况下,燃料芯体内部颗粒破裂的比例很高,大量微裂纹贯穿、连通扩展至基体,最终宏观表现为包壳表面起泡,可认为燃料颗粒的开裂失效是弥散燃料失效的根源[4-5]。
为研究弥散燃料的失效行为,需建立相应的理论模型,发展有效的数值模拟方法,学者们在这方面开展了许多有意义的工作。Rest等[6-8]研究了燃料内裂变气体肿胀模型的计算以及U-Mo合金中裂变气泡尺寸分布规律与高温成核机制。万远富等[9]利用Eshelby等效夹杂理论,在考虑温度场和辐照肿胀的条件下,分析了颗粒的形状以及辐照肿胀对应力状态的影响。龙冲生等[10]在裂变气孔尺寸均匀分布的条件下利用弹性力学建立了弥散燃料颗粒开裂模型,系统计算预测了燃料颗粒的开裂规律。Jeong等[11-12]建立了弥散燃料的局部应力失效分析模型,并用有限元模型模拟了燃料基体和颗粒的热-力学行为。Ding等[13-15]采用代表性体元并假设燃料颗粒均匀分布,建立了细观有限元模型,分析了细观热-力学行为和辐照蠕变行为对弥散型板状燃料元件可靠性的影响。赵毅等[16-18]基于数值模拟对高燃耗结构的燃料颗粒内部气孔力学行为进行研究,建立了双气泡和均匀分布的多气泡模型,讨论了燃料颗粒内部气孔的尺寸、分布等对其应力分布的影响,得到了燃料颗粒裂纹起源是在表层气泡内壁的结论。目前的研究都是基于颗粒或气孔均匀周期性分布情况下展开的,这与实际不符,开展考虑燃料颗粒内部非均匀性的数值模拟,能更好地反映颗粒的强度特性。
本文基于随机序列吸附法(RSA)思想实现含弥散非均布的裂变气孔的高燃耗陶瓷燃料颗粒的几何建模,并结合ABAQUS有限元软件二次开发实现燃料颗粒静力学分析的参数化建模。分析关键参数气孔尺寸、温度、及颗粒所受基体材料约束压应力对燃料颗粒内部最大拉应力的影响规律,并对燃料颗粒内部危险区的分布进行讨论。
1 燃料颗粒参数化建模
弥散燃料芯体中的每一个燃料颗粒都可单独看作1个微型燃料元件,在辐照条件下燃料颗粒内部弥散分布了大量的气孔。在高温和高燃耗条件下,气孔内部裂变气体的压力会达到上百MPa[19],气孔的尺寸和位置分布均会改变燃料颗粒内部应力场的分布,进而影响开裂行为。考虑这些参数的影响必须参数化建模,通过参考辐照后高燃耗燃料颗粒微观形貌的电镜照片可知,燃料颗粒及其内部弥散分布的小气孔近似为球形[20]。因此,本文对燃料颗粒进行抽象与简化(图1):1) 燃料颗粒为球形,颗粒由致密的燃料相和离散的裂变气孔两相组成;2) 燃料颗粒外表面受到均布的约束压应力pf,源于基体材料对燃料相肿胀变形的约束作用,弥散气孔内表面受到均布的气体压应力pg作用。

图1 高燃耗燃料颗粒的抽象与简化Fig.1 Abstraction and simplification of high burnup fuel particle
文献[21]利用对数正态分布对燃料颗粒中的气孔半径数据进行过拟合,但这种方法对不同燃耗的适用范围有要求。本文采用适应性更强的Weibull分布来描述气孔尺寸及气孔间距的分布规律。Weibull分布的概率密度函数如下:
(1)
式中:x为随机变量,本文中代表气孔半径或气孔间距;λ为尺度参数,反映变量的平均特性;k为形状参数,反映变量的非均匀性,k越大则离散性越小。当k取不同值时,可得到正偏、负偏和对称的概率密度函数。
参数化建模流程如图2所示。首先,基于RSA思想,运用Python编程手段,在燃料颗粒内部投放小气孔,并记录气孔的坐标和半径,此过程保证气孔相互不重叠,并控制气孔半径(r)和相邻气孔间距(d)都服从Weibull分布,分别用Weibull-r和Weibull-d表示,以颗粒半径160 μm、平均气孔半径2 μm的模型为例,所绘效果图如图3所示。然后,使用Python脚本语言对ABAQUS有限元进行二次开发,建立颗粒几何模型,并实现程序化加载、划分网格和静力学计算。

图2 参数化建模流程Fig.2 Parametric modeling process

图3 气孔尺寸和位置非均匀分布的 高燃耗燃料颗粒模拟效果图Fig.3 Simulation effect picture of high burnup fuel particle with heterogeneous distribution of pores
2 数值模拟
2.1 燃料颗粒的力学参数
UO2陶瓷核燃料具有耐高温、耐辐照、肿胀小、包容裂变产物性能好等优点,能达到高燃耗的状态,是目前应用最广泛的陶瓷核燃料。本文针对高燃耗状态下的UO2燃料颗粒开展数值模拟研究,定性分析关键参数对燃料颗粒开裂的影响规律。作为陶瓷型核燃料,UO2燃料颗粒从辐照初始状态到高燃耗断裂失效,致密的燃料相都处于弹性阶段,不考虑其塑性变形行为。目前对于辐照后陶瓷颗粒的力学性能研究较少,本文参考文献[10]中陶瓷的弹性模量E与燃耗和温度T的关系式:
E=162 000+63 000/
(1+35BU)-20(T+273)
(2)
其中:BU为燃耗深度,FIMA;T为温度,℃。
燃料颗粒中裂变气孔体积分数ρg与燃耗的关系为:
ρg=0.021+0.66BU
(3)
有限元模型中气孔的最大尺寸与最小尺寸相差倍数不大,所以假设颗粒内部气孔的内压大小相同,气孔内压pg采用超高压下实际气体的状态方程计算:
(4)
(5)
其中:ng为裂变气体总量;Vg为气体总体积;R=8.31 J/(mol·K)为气体常数;a=5.57×10-5m3、b=2.39×10-5m3为实际气体状态方程参数;Df=10.96×106/(1+ρg)为燃料颗粒的密度,g/m3;β为裂变气体(Xe+Kr)的裂变产额;Mf=269 g/mol为燃料相的摩尔质量。
此外,认为图1所示裂变气孔内压作用的致密燃料相球壳内壁的拉应力大于UO2燃料相的断裂强度时,燃料颗粒开裂,即选用第一强度理论作为UO2燃料颗粒的开裂判据。对应有限元模拟研究中,计算得到燃料颗粒内部气孔相互干涉的第一主应力场,其中最大应力点处即为整个燃料颗粒最大拉应力位置。
2.2 有限元模型
本文选取的高燃耗燃料颗粒尺寸Rf定为160 μm,弥散气孔尺寸Rg也在实验观测范围内。欲建立高温、高燃耗UO2燃料颗粒的全尺寸仿真计算模型,还需对各气孔内壁和颗粒外表面施加均匀压力(图4),载荷数值由程序代码计算并控制施加,运用有限元求解得到应力场。此外,由于本研究有限元模型中考虑了气孔尺寸和分布位置的非均匀性,致使燃料颗粒内部的结构非常复杂,为保证计算结果的精确性,在有限元网格划分过程中,采用四节点平面应力缩减积分单元CPS4R,对所有的气孔孔壁和燃料颗粒外表面进行加密分割,完成网格划分后,每个模型的单元数都在20万以上。

图4 高燃耗UO2燃料颗粒有限元模型的 加载方式Fig.4 Loading mode of high burnup UO2 fuel particle
3 结果分析与讨论
3.1 气孔尺寸对燃料颗粒最大拉应力的影响
为方便定性分析,参数化建模过程中保证颗粒内部气孔间距满足一致的非均匀分布形式,而气孔尺寸相同,选取的气孔半径Rg分别为0.8、1.2、1.6、2.0、2.4 μm,利用有限元法计算不同模型的最大拉应力。基于蒙特卡罗方法[22],在给定气孔率和气孔间距满足Weibull分布形状参数的情况下,对每种气孔尺寸的颗粒模型建立多个随机模型,取计算结果的平均值作为有效数据。其中,仿真模型的材料参数由式(2)~(5)计算得到,具体如下:颗粒半径,160 μm;温度,600 ℃;气孔率,20%;基体压应力,0.1 MPa;弹性模量,156 .4 GPa;泊松比,0.316。
在给定气孔率ρg、温度T、燃耗BU和基体压应力pf的情况下,燃料颗粒内部的最大拉应力随气孔半径的变化规律如图5所示。由图5可知,气孔尺寸增大,颗粒的最大拉应力随之增大,即当气孔半径由0.8 μm增大到2.4 μm时,最大拉应力从222.7 MPa增大到484.5 MPa。此过程是非线性变化的,气孔尺寸越大,最大拉应力增加的幅度越大。如气孔尺寸从0.8 μm变化到1.2 μm时,最大拉应力增大34 MPa,气孔尺寸从2.0 μm变化到2.4 μm时,最大拉应力增加122.1 MPa。基于以上结果,可认为太小的气孔对燃料颗粒开裂失效的影响不大,大尺寸气孔对燃料颗粒开裂失效的影响更显著。
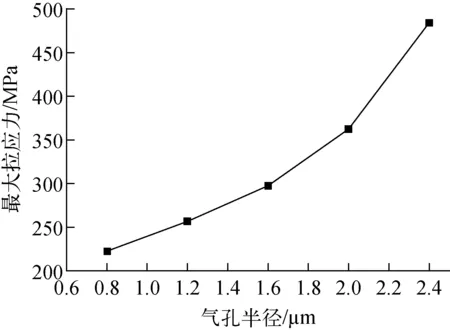
图5 气孔半径对最大拉应力的影响Fig.5 Influence of pore radius on maximum tensile stress
有限元计算的最大拉应力云图示于图6。由图6可看出,不同气孔尺寸的燃料颗粒最大拉应力出现在靠近颗粒表层,而从高燃耗燃料颗粒的电镜照片[5]可知,燃料颗粒也确实多从表层附近开始起裂,本研究结果与辐照实验观察结果具有一致性。

图6 最大拉应力出现位置Fig.6 Position of maximum tensile stress
3.2 基体约束压应力对燃料颗粒最大拉应力的影响
燃料元件在堆内服役时受到的环境静水压力通过基体的传递最终作用在燃料颗粒上,此外颗粒辐照肿胀也会受到基体的束缚,所以可将基体材料对燃料颗粒的约束压应力pf看作燃料颗粒开裂行为的阻力,它与颗粒的强度密切相关[23]。选取气孔半径Rg=2.4 μm的燃料颗粒模型控制变量分析最大拉应力的变化趋势,取pf为1、10、20、30、40、50 MPa进行有限元计算,其余材料和模型参数不变,研究pf对颗粒强度的影响,结果示于图7。分析图7可知,在给定气孔率ρg、燃耗BU、温度T、气孔半径尺寸Rg的情况下,基体对燃料颗粒的约束压应力pf越大则燃料内部最大拉应力越小;pf由1 MPa增大到50 MPa时,最大拉应力近似线性减小了128.5 MPa。可见基体约束压应力pf对UO2燃料颗粒的开裂行为影响很大,不可忽略。
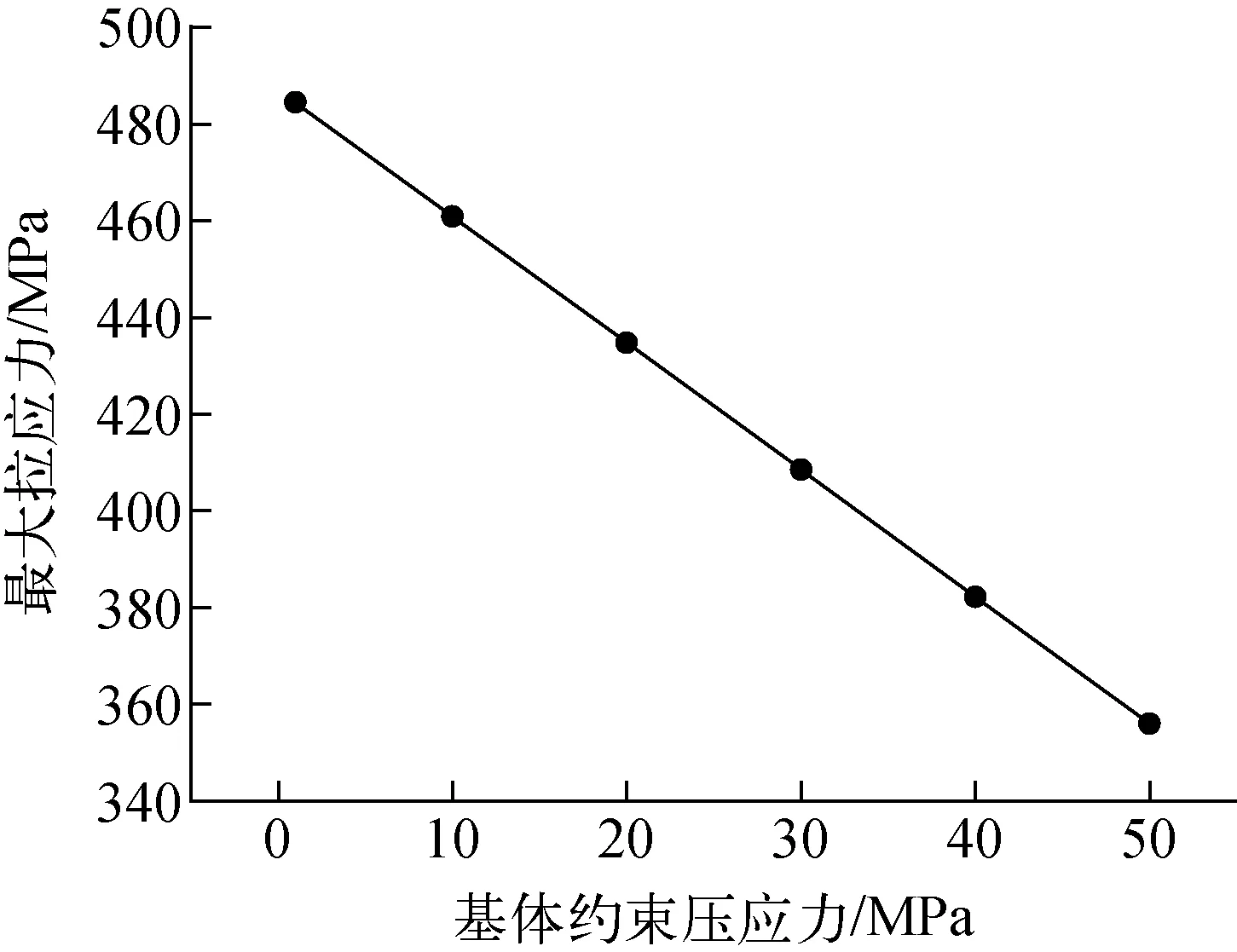
图7 基体约束压应力对最大拉应力的影响Fig.7 Influence of constrained compressive stress of matrix on maximum tensile stress
3.3 温度对燃料颗粒最大拉应力的影响
堆内运行工况下,燃料颗粒处于高温状态,且温度是变化的,通常与燃料颗粒在燃料元件中的分布位置和运行工况有关。因此,有必要分析温度变化对燃料颗粒强度的影响。对于气孔尺寸和间距均满足Weibull分布且气孔平均半径为2.4 μm的燃料颗粒,在给定ρg为20%、pf为0.1 MPa时,温度增大,其内部最大拉应力的变化规律如图8所示。图8表明,气孔尺寸Weibull分布参数λ和k不同时,燃料颗粒内部最大拉应力均随温度升高而增大,且均近似呈线性关系。从图8还可知,温度是燃料颗粒失效的敏感参数,温度从300 ℃上升到700 ℃时,最大拉应力增加超过200 MPa。如气孔尺寸Weibull分布形状参数k=7时,最大拉应力随温度升高而增大了241.3 MPa。形状参数k反映气孔尺寸分布的离散性,从结果分析可知k越小,相同温度条件下,最大拉应力越大。原因是形状参数k越小,气孔尺寸分布越离散,这会增大大尺寸气孔的比例。

图8 温度对最大拉应力的影响Fig.8 Influence of temperature on maximum tensile stress
3.4 燃料颗粒内高应力区的分布
在辐照条件下,UO2陶瓷燃料相本身的断裂强度σf会随微结构变化[24]。本文定义陶瓷燃料颗粒内部超过燃料相断裂强度的区域为高应力区域,即开裂危险区,裂纹先从这些区域产生。在给定气孔率、燃耗深度、温度、基体约束压应力、气孔尺寸和间距都非均匀分布的条件下,改变陶瓷燃料相的断裂强度,考察高应力区的分布,结果如图9所示。分析可知,当气孔内压一定,陶瓷燃料相的断裂强度从275 MPa减小到175 MPa时,高应力(红色)区域的面积增大;从图9也可看出高应力区的演化过程,首先开裂危险区先从陶瓷燃料颗粒的表层多处出现,然后在颗粒内部某些地方也出现开裂危险区,之后这些区域相互连通,甚至可将颗粒贯穿。此外,尺寸较大气孔边缘的高应力区面积更大,也更易与其周围的气孔连通。综上所述,在辐照条件下,由于气孔尺寸和位置非均匀分布,颗粒内部应力干涉效应复杂,致使颗粒的危险区从多处出现,即颗粒是从多处开裂破坏的。

图9 燃料相断裂强度不同时高应力区域的分布Fig.9 Distribution of high stress regions with different fracture strengths of fuel phase
3.5 气孔分布方式对燃料颗粒最大拉应力的影响
高燃耗结构的气孔尺寸和位置本身是随机分布的,因此这种模型孔间产生干涉效应是复杂的,相较于传统的气孔均匀分布燃料颗粒模型,二者内部的应力场存在差异。本文参照文献[17]的气孔分布方式建立气孔均匀分布的燃料颗粒模型,通过有限元计算得到应力云图,如图10所示。对与上述模型具有相同气孔率、内压载荷、约束条件的气孔非均分布的颗粒模型进行计算。其中非均匀分布的颗粒模型在给定气孔分布参数的情况下随机生成7次,得到7组计算数据,将其与均匀分布的模型进行对比,结果如图11所示。

图10 气孔位置均匀分布的燃料颗粒模型应力云图Fig.10 Stress contour of fuel particle model with uniform arrangement of pore position
图11表明,非均匀分布的最大拉应力较均匀分布模型的大,更易开裂,且非均匀分布的燃料颗粒内部的高应力区是多处存在的,更能反映高燃耗燃料颗粒多处开裂的物理现象,而均匀分布的颗粒模型没有此现象。

图11 气孔均匀分布与非均匀分布模型结果对比Fig.11 Comparison of model results of uniform and non-uniform arrangement of pores
4 结论
本文结合Python语言和有限元二次开发,实现了气孔尺寸和位置非均匀分布的高燃耗陶瓷燃料颗粒参数化建模,基于有限元技术对陶瓷燃料颗粒的强度和开裂影响因素进行了分析研究,得到如下主要结论。
1) 在给定气孔率、燃耗深度、温度、基体约束压应力,且仅考虑气孔位置非均匀随机分布的条件下,燃料颗粒内最大拉应力随气孔尺寸的增大而增大,且大尺寸气孔对最大拉应力的影响更大;在给定气孔率、燃耗深度、温度、气孔尺寸,且仅考虑气孔位置非均匀随机分布的条件下,燃料颗粒内最大拉应力随基体约束压应力的增大近似线性减小。
2) 本研究有限元模型中考虑了温度这一重要开裂影响参数,同时模拟计算了气孔尺寸和非均匀随机分布下的应力场,发现燃料颗粒内最大拉应力受温度影响显著,且随温度升高而近似线性增大。
3) 在气孔尺寸和间距都非均匀分布的条件下,改变陶瓷燃料相的断裂强度能得到高应力区的演化过程。颗粒内部应力干涉效应复杂,致使多处出现颗粒开裂的危险区域,即颗粒是从多处开裂破坏的,而气孔均匀分布的燃料颗粒模型没有这种现象。
高燃耗燃料颗粒在堆内运行环境下的开裂行为是多因素耦合作用的结果,本研究基于有限元理论结合Python语言,为系统分析这种复杂失效行为提供了技术支持,也为进一步研究整个弥散燃料元件的辐照性能奠定了基础。