基于GNSS技术的波浪浮标测波方法研究
2021-10-09李梦昊刘焱雄
田 力,刘 杨*,李梦昊,2,刘焱雄
(1.自然资源部 第一海洋研究所,山东 青岛266061;2.河海大学 地球科学与工程学院,江苏 南京210098)
在海洋工程建设、海洋灾害预防、航海安全等领域中,波浪是重要且复杂的一种海洋气象要素[1]。发展海洋是增强我国经济实力、政治地位和国际影响的重要途径。通过加强海洋监测来增强海上的防御能力,对增强我国的国防建设有着十分重要的意义。此外,近海波浪的监测研究对海况预报、海上运输、海洋开发和海洋渔业等活动也都有非常重要的影响,加强与完善我国现场波浪观测已成为我国海洋研究的重要课题[2-3]。
波浪是海洋中的重要运动现象,监测波浪的变化并研究其运动规律,对人类在海上活动及近岸活动具有重要的意义。近几十年来,人类对海洋开发活动的增加促进了海洋观测方法的研究和仪器设备的研制。目前,常见测波仪器有加速度式测波仪、压力式测波仪、声学测波仪及全球导航卫星系统(GNSS)测波浮标等[4]。其中,GNSS测波浮标利用了全球导航卫星系统获取浮标载体的三维空间位置、速度和时间信息,测波浮标具有良好的随波运动特性,可以通过位置信息有效反演波浪要素。GNSS测波浮标结合卫星导航定位技术,可有效观测波浪信息,而且具有系统简单、成本低、体积小等优点[5]。
由于GNSS技术的限制,如RTK(Real-Ti me Kinematic)实时载波相位差分技术和PPK(Post-Pr ocessing Kinematic)动态后处理差分技术均可得到厘米级定位结果,但都依赖于基站,有效作用距离限制在几十公里,无法应用于远海场景。PPP(Precise Point Positioning)精密单点定位技术不受基站距离限制,是一种被广泛采用的GNSS测波技术,目前已有很多学者做过相关研究。程世来和张小红[6]提出了利用精密单点定位技术结合Trip软件对实测浮标数据进行处理,探讨了海啸预警的新方法。邱冠维[7]研究了利用精密单点定位技术进行GPS浮标近实时精密定位,并与DGPS观测资料和潮位站观测资料进行了对比,证明了采用精密单点定位技术进行波浪测量的可行性。然而,PPP技术仍存在很多劣势,卫星轨道和钟差产品的精度是影响PPP定位精度的重要因素,而这类产品一般存在时间延迟,制约了实时场景的应用。实时高精度PPP方法需要额外的实时精密差分改正数产品,在海上应用时极大增加了精密差分改正服务的成本和通讯的成本。
综上所述,为了实现实时厘米级的波浪测量精度,若将波浪浮标GNSS观测值传回数据处理中心进行实时解算,需要大量的通讯带宽,从而产生了通讯成本,尤其是远海卫星通讯成本,而且由于通讯降低了实时性;若将波浪浮标GNSS观测值在浮标本地进行实时解算,则需要额外的差分改正服务,其中,在近海需要与陆地通讯获得差分改正服务,在远海需要从通讯卫星获得差分改正服务,这增加了购买差分改正服务和通讯的成本。所以,目前传统的GNSS测波方法在实时高精度波浪测量方面存在极大劣势和限制。随着GNSS技术的发展,研究更为高效、低成本的实时高精度波浪测量方法,是提高海洋波浪测量业务实时性、高精度能力,为全球海洋波浪要素信息获取提供技术支持的重要手段。
本文研究了一种基于GNSS技术的实时高精度波浪测量方法,获取的波浪要素信息可以存储于本地或者通讯传回,并以2020年10月底南海现场浮标试验所得数据为例进行了处理和分析,验证了该方法的可行性。
1 GNSS实时高精度波浪测量方法
本文方法是一种基于GNSS技术的实时高精度波浪测量方法,主要由两部分组成,一是载波相位历元差分法实时求解浮标运动水平和垂直的三维运动速度,二是通过波浪反演算法由位移信息反演得到波浪要素信息。
1.1 载波相位历元差分法
首先,采用搭载GNSS接收机的波浪浮标等海面载体,实时采集高频GNSS的定位电磁波信号,将其转换为相位、伪距、多普勒频移观测值和广播星历发送至波浪浮标的处理器;其次,利用基于广播星历和建立的相位历元差分观测方程,顾及误差项的处理,实时求解浮标运动水平和垂直的三维运动速度;最后,通过求得的浮标的垂向、东西向、南北方向的速度,采用滑动时间窗口的方法,对垂直运动速度进行一定时长的积分,并去除由系统误差与潮汐导致的趋势项或采用直接去除线性趋势项,得到垂向位移随时间变化信息。
其中,基于广播星历和建立的相位历元差分观测方程为利用广播星历的历元差分载波相位观测方程,其方程如下:
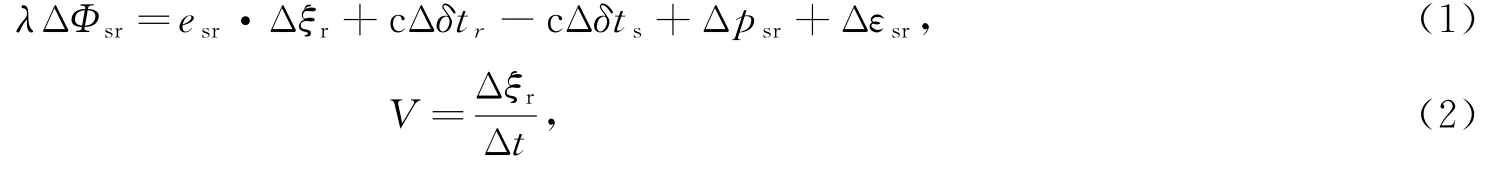
式中:λ为载波频率;ΔΦsr为从卫星S到接收机r的相邻历元的载波相位观测值之差;esr为从卫星S到接收机r的单位矢量;Δξr为相邻历元之间接收机的位移增量;c为光速;Δδtr、Δδts分别为相邻历元之间的接收机时钟偏差、广播星历计算的卫星时钟偏差;Δpsr为相邻历元之间的综合误差改正,包括卫星轨道、电离层、对流层、相位中心变化、相位缠绕、相对论效应、地球自转效应等,其中卫星轨道改正由广播星历计算,电离层改正由双频无电离层组合消除一阶项,对流层改正由气象数据(实测值或者模型值)及投影函数改正,相位中心变化由天线模型计算,相位缠绕、相对论效应、地球自转效应等由相应模型计算;Δεsr为其他残余误差项与噪声;V为三维速度;Δt为相邻历元之间的时间间隔。
由于速度受海况、浮标位置、信号误差和其他噪声的影响,速度数据含有误差,积分方法将积累误差,速度反演的位移数据存在趋势项,同时潮汐的水位变化也会导致垂向位移的趋势项[8-11]。本方法在剔除速度粗差的基础上,采用滑动窗口平均的方法,例如每10~20 min的时段,将所得到的位移去掉线性趋势项,进而得到波浪的位移信息。
1.2 波浪反演算法
波浪核心要素信息包括波高、周期等,波高和波浪周期与波浪垂直位移有关,本方法采用跨零法、谱分析方法从去除趋势项后的垂直位移中提取波高及波浪周期参数,具体包括十分之一大波波高及其对应周期、有效波高及其对应周期、平均波高及其对应周期等。采用谱分析方法,由位移时间序列得到波浪参数,计算公式见式(3)~式(7)[8-11]:
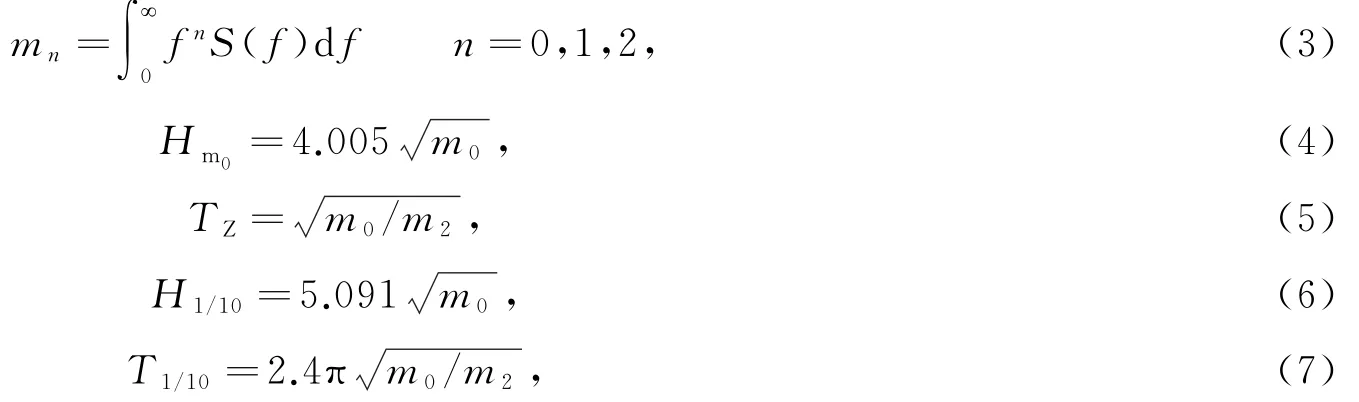
式中:f为频率;S(f)为功率谱密度;mn为n阶谱矩;Hm0为由频谱得到的有效波高;TZ为平均周期;H1/10为十分之一最大波高;T1/10为十分之一最大波高周期。
由于一般波浪周期为1~30 s,本方法实施时可采用高通滤波器消除低于0.03 Hz频率的低频噪声数据,GNSS接收机采样频率一般设置为5~20 Hz,本方法求得的上述波浪信息可存储于浮标本地,或者实时、定期通讯传回。
2 试验数据
本文数据来源于2020年10月底自然资源部第一海洋研究所组织实施的南海浮标试验,试验区位于广东茂名博贺近岸海域,具体位置见图1。浮标采用锚系的形式布放在船只周围,试验现场浮标布放情况见图2,试验中GNSS多功能浮标运行轨迹以及高程变化见图3。本试验采用了2种不同类型的GNSS浮标:GNSS多功能浮标和波浪骑士公司的DWR-G4波浪浮标。其中,GNSS多功能浮标采样频率为5 Hz,质量约50 kg,直径约0.5 m;波浪骑士DWR-G4浮标采样频率为2 Hz,质量约17 kg,直径约0.4 m。
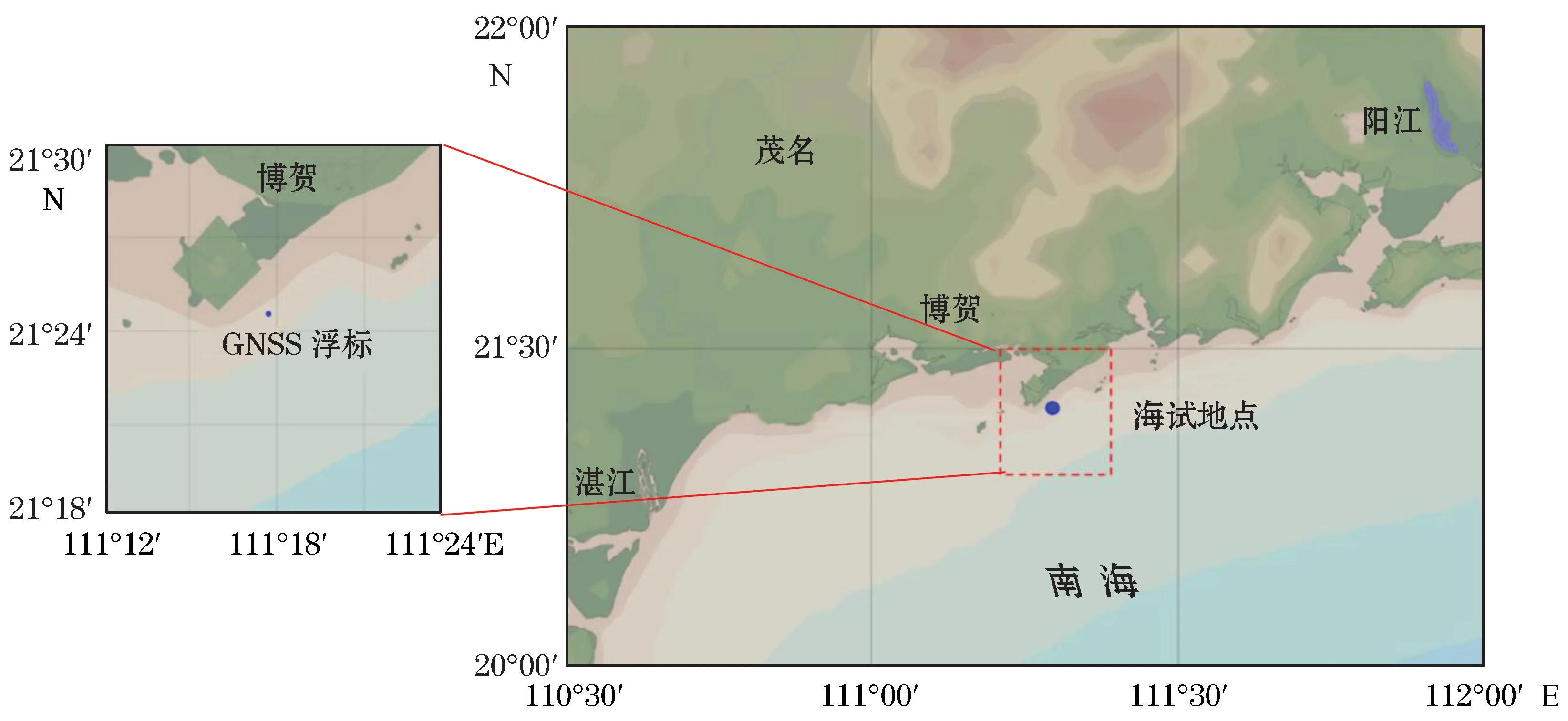
图1 海试地点Fig.1 Buoy mooring field

图2 浮标布放现场Fig.2 Location of the sea test
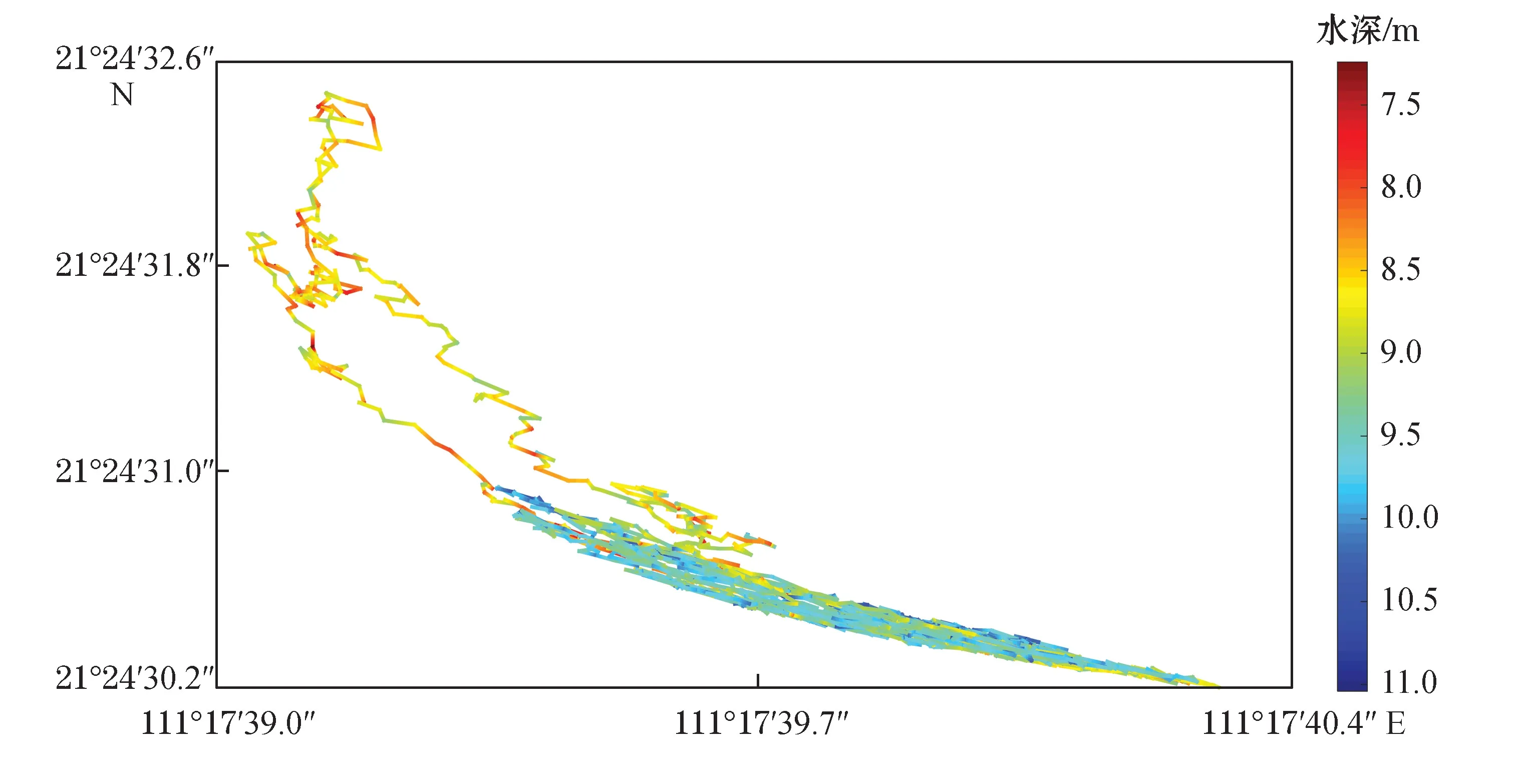
图3 GNSS多功能浮标运行轨迹与高程变化Fig.3 Tracks and elevations of the multi-f unctional GNSS buoy
本文处理的数据所取时间段2020-10-28 T06:30—2020-10-28T22:00,分别采用精密单点定位(PPP)方法和载波相位历元差分法对GNSS多功能浮标该时间段原始数据进行处理,再通过波浪反演算法得到所需的波浪要素结果,与波浪骑士DWR-G4波浪浮标结果进行对比,验证GNSS测波方法的可靠性。
3 结果与分析
3.1 波浪要素反演结果对比
对2020-10-28 T06:30—2020-10-28T22:00这一时间段的GNSS多功能浮标原始数据进行解算,分别采用精密单点定位(PPP)方法以及载波相位历元差分法对GNSS多功能浮标该时间段原始数据进行处理,得到相应的位置信息结果,再通过波浪反演算法得到所需的波浪要素结果,与波浪骑士DWR-G4波浪浮标官方软件处理结果进行对比。
首先对该时间段基于广播星历历元差分与基于精密星历精密单点定位(PPP)处理得到的垂向速度进行比较(图4),其中PPP的速度由原始位移的数值微分得到。由图4可知,基于广播星历历元差分得到的速度结果与PPP结果大体一致。
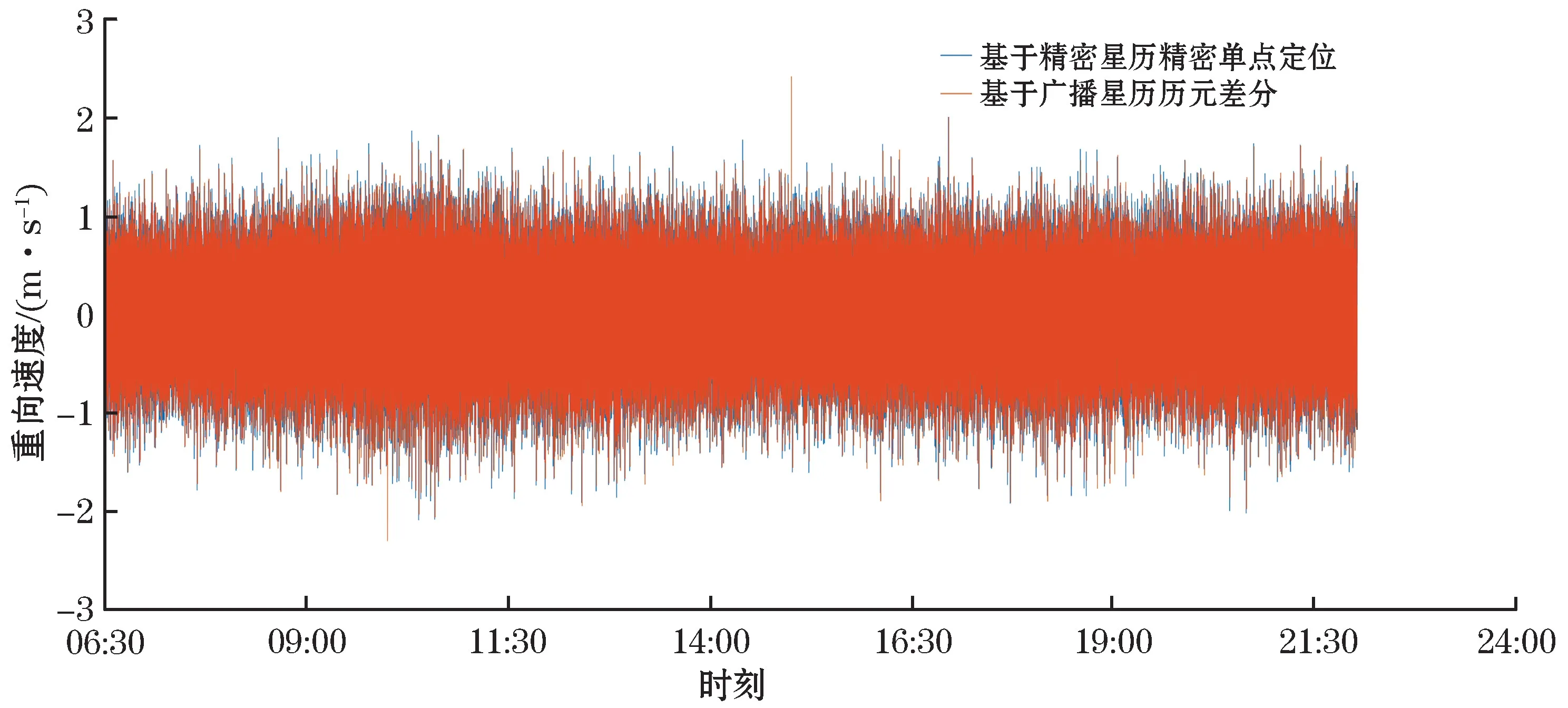
图4 垂向速度变化Fig.4 Changes in vertical velocity
本研究共对比了5个波浪要素信息:有效波高(H )、平均周期(T)、十分之一最大波高(H/)、十分之一最大波高周期(T1/10)和跨零法有效波高。由于波浪骑士DWR-G4浮标官方软件处理所得结果为0.5 h对应一组波浪参数,为保证与其时刻一一对应以便于对比,设置滑动时间窗口为0.5 h。各波浪要素对比结果见图5。
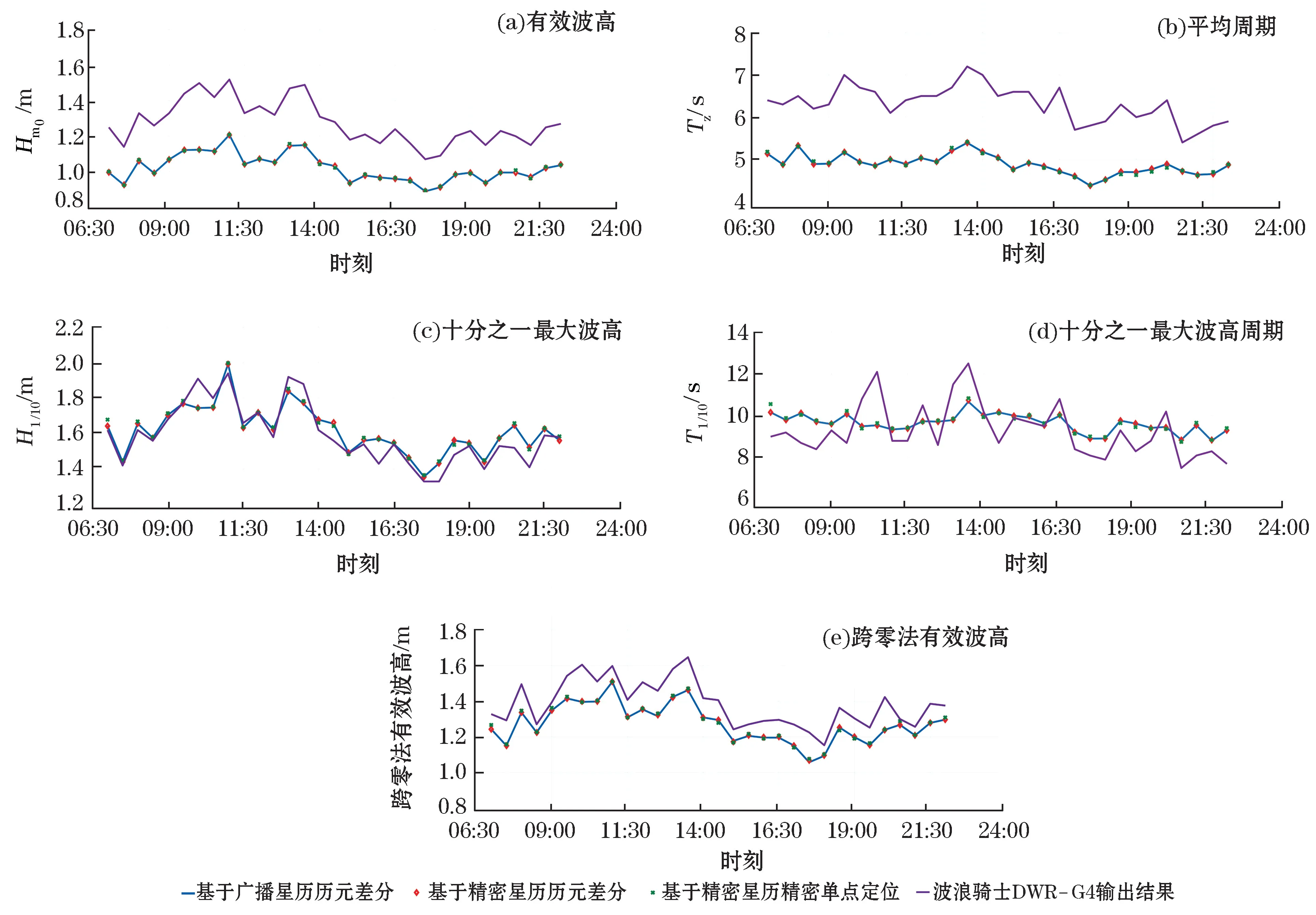
图5 各波浪要素对比Fig.5 Co mparison of wave elements
由图5a可知,波浪骑士DWR-G4波浪浮标有效波高结果略高于GNSS多功能浮标的有效波高反演算法结果,其中波浪骑士浮标有效波高均值为1.022 m,GNSS多功能浮标的有效波高均值为1.276 m,高出约25 c m;由图5b可知,波浪骑士DWR-G4波浪浮标平均周期结果略高于GNSS多功能浮标的平均周期反演算法结果,其中波浪骑士浮标平均周期均值为4.885 s,GNSS多功能浮标的平均周期均值为6.316 s,高出约1.5 s。
由图5c可知,波浪骑士DWR-G4波浪浮标结果与GNSS多功能浮标的反演算法结果总体吻合,其中波浪骑士浮标的十分之一最大波高均值为1.593 m,GNSS多功能浮标的十分之一最大波高均值为1.616 m;由图5d可知,波浪骑士DWR-G4波浪浮标结果与GNSS多功能浮标的反演算法结果均值相差不大,但对应时刻数值有较大差异,表现为围绕GNSS多功能浮标结果上下波动,其中波浪骑士浮标的十分之一最大波高周期均值为9.3 s,GNSS多功能浮标的十分之一最大波高周期均值为9.641 s,相差约0.3 s。
由图5e可知,波浪骑士DWR-G4波浪浮标结果略高于GNSS多功能浮标的反演算法结果,其中波浪骑士浮标跨零法有效波高均值为1.383 m,GNSS多功能浮标的跨零法有效波高均值为1.274 m,相差约0.1 m。
为进一步分析GNSS测波方法精度,本文统计了GNSS多功能浮标基于广播星历产品的历元差分方法反演得到的各波浪要素相对于波浪骑士DWG-G4浮标波浪要素的差值百分比(表1)。

表1 两浮标各时间段波浪要素差值百分比(%)Table 1 Percentages of the differences bet ween the wave elements of t wo buoys at each ti me periods(%)
由表1可知,两浮标的Hm0与Tz的差值百分比约为20%,两浮标的H1/10、T1/10和跨零法有效波高的差值百分比基本上在10%,进一步说明了两浮标的波浪要素反演结果较为接近,采用载波相位历元差分法的波浪反演结果较为可靠。
本文分析了两种浮标波浪参数反演结果的相关性。根据相关系数绝对值(|r|)划分相关程度:微相关(0.00~0.30)、实相关(0.30~0.50)、显著相关(0.50~0.80)和高度相关(0.80~1.00)。
本文统计了波浪骑士DWG-G4浮标与GNSS多功能浮标基于广播星历产品的历元间差分方法的相关系数,二者反演得到的各波浪要素相关系数(表2)。由表2可知,波浪骑士浮标的波浪要素结果和GNSS多功能浮标的波浪要素结果普遍存在显著相关关系,其变化趋势具有高度一致性。

表2 两浮标各波浪要素的相关系数Table 2 Correlation coefficients of the wave elements of t wo buoys
3.2 试验分析
对比GNSS多功能浮标不同解算方法的各波浪要素结果可知,基于广播星历产品、基于IGS精密星历产品的历元间差分方法和基于IGS精密星历产品的精密单点定位方法得到的各波浪要素信息结果基本吻合,数值与总体变化趋势均吻合良好,验证了历元差分方法的可靠性,证实了基于广播星历的历元差分方法可获取高精度的波浪信息。
对比GNSS多功能浮标和波浪骑士浮标的各波浪要素结果可知,波浪骑士浮标的波浪要素结果总体略高于GNSS多功能浮标波浪要素结果,两者总体较为吻合(图5、图6和图9),且波浪骑士浮标的波浪要素结果和GNSS多功能浮标波浪要素结果存在显著相关关系,其变化趋势具有高度一致性,可以说明利用该方法得到的波浪要素结果较为准确。本试验中波浪骑士浮标的波高结果略高于GNSS多功能浮标的波高结果,可能是因为GNSS多功能浮标整体体积和重量均大于波浪骑士DWR-G4浮标,导致随波性不够好,致使波浪要素信息反演结果出现一定偏差。
4 结 语
本文研究了一种可实时得到波浪要素信息的GNSS高精度波浪测量方法,并且以2020年10月底南海现场浮标试验所得数据为例进行了处理和分析。结果表明,该方法可反演得到包括有效波高、平均周期、十分之一最大波波高、十分之一最大波周期等多种波浪要素信息,与波浪骑士浮标反演结果的对比说明该方法所得波浪要素信息较为准确。与基于IGS精密星历产品的历元间差分方法、基于IGS精密星历产品的精密单点定位方法结果对比说明,采用基于广播星历的历元差分方法可以得到高精度的波浪要素信息,验证了该方法的有效性。
本文的方法直接基于广播星历进行GNSS相位观测值历元差分确定速度,无需额外的精密差分改正数,从而节省了浮标等海面载体的精密差分改正服务成本与通讯成本。该方法可适用于近海、远海场景,可实时直接得到波浪要素信息,扩大了基于GNSS技术的海洋波浪测量的工作范围。采用该方法的浮标等海面载体可以搭载低成本单频GNSS接收机,得到高精度波浪测量结果,具有较高的实际应用价值,为海浪浮标的设计与研究提供参考。本研究仅解算得到了部分波浪要素信息,蕴含更为丰富海浪信息的方向谱反演仍需进一步的研究。
