Φ 1650 mm口径反射镜的坦克链支撑研究∗

2021-10-09宫雪非

天文学报 2021年5期

关键词：反射镜钢带滚子

张俊宫雪非

(1 中国科学院国家天文台南京天文光学技术研究所南京 210042)

(2 中国科学院天文光学技术重点实验室(南京天文光学技术研究所)南京 210042)

(3 中国科学院大学北京 100049)

1 引言

随着反射镜的口径不断增大,因为重力作用导致的镜面变形问题就越严重.本文研究的Φ 1650 mm口径反射镜是某套大口径精密光学元件检测系统中的定标校正模块,系统提出的技术指标为:面型均方根误差(Root Mean Square,RMS)小于1/70波长,这其中包含了镜面的加工误差和支撑误差.工作时反射镜在光路中竖直放置,光轴始终保持水平状态.

针对镜面始终保持光轴水平的工作条件,国内外专家学者都对大口径镜面的侧支撑技术做出了仔细深入的研究.目前具有代表性的侧支撑技术有杠杆平衡重支撑、水银带支撑以及钢带支撑.朱星申等[1]针对大口径透镜提出了杠杆平衡重支撑方案,优化了支撑点的数量、支撑力与支撑位置,引入了透射波前像差的概念,得到了理想的面型精度.陶天奇[2]对主镜采用水银带径向支撑,并对水银的充满度、承担主镜质量的比例、支撑位置进行了优化分析,满足了预期的技术要求.李睿等[3]利用有限元方法,研究了Φ 600 mm口径反射镜钢带支撑方案,并与环形支撑、3点支撑进行对比,得出了钢带支撑结构下的反射镜应力变化更加均匀的结论.

上世纪90年代初期,Vukobratovich和Richard[4]提出一种新型的坦克链支撑技术并成功运用于实践,在国内外广泛应用.刘兆栋[5]在Φ 600 mm口径的干涉仪设计研制过程中,对比分析了Φ 600 mm口径平镜在钢带支撑和坦克链支撑条件下的面型及最大等效应力,对坦克链的宽度、中心距进行了优化,并进行了最大许用应力校核,保证方案的可靠性.Fitzsimmons等[6]针对Φ 660 mm口径反射镜提出了坦克链支撑结构,并基于赫兹接触理论,对坦克链滚子与反射镜边缘的非线性接触进行了模型简化,减少计算量并保证计算结果的收敛.

本文以位于光学检测系统中的Φ 1650 mm口径反射镜为研究对象,根据反射镜的工作状态与技术指标,最终确定采用坦克链径向支撑结构,并与传统的钢带支撑结构进行了对比,对坦克链支撑的优势进行了深入的研究.

坦克链支撑的具体方案是采用两条钢制坦克链,按反射镜重心平面对称安装布置.坦克链支撑具有明显的优点:可以通过调节坦克链的轴向位置,降低反射镜侧面滑脱的风险,提高了反射镜的空间稳定性;将连续的面支撑转变为离散支撑,镜面与坦克链滚子的摩擦力更小;可以采用成熟的商业产品,如市场上常见的超大滚子坦克链,产品尺寸和型号多样,价格相对便宜.缺点在于:坦克链滚子与反射镜边缘的非线性接触,会产生较大的应力而导致镜面边缘破碎.通过选择合适的坦克链类型以及精细地调整坦克链滚子位置等措施,可以有效降低反射镜破碎的风险[4].

Φ 1650 mm口径反射镜在坦克链支撑结构下,面型精度达到了工程设计要求,经过校核,最大等效应力值也在许用应力范围之内.坦克链支撑是一种理想的大口径反射镜侧支撑方案.

2 反射镜模型参数

该平凹反射镜口径1650 mm、曲率半径63 m、边缘厚度240 mm、矢高5.4 mm.材料选用微晶玻璃,材料参数如表1所示.

表1 微晶玻璃材料参数Table 1 Properties of Zerodur

3 钢带支撑

钢带支撑是在光学检验车间最常用最简易的方案,具体操作是将反射镜通过钢带悬挂固定在支撑框架内,如图1.这种装置结构简单、造价适中、受力均匀,适合在地面设备上使用[7].本文将对钢带支撑与坦克链支撑进行深入的分析比较.

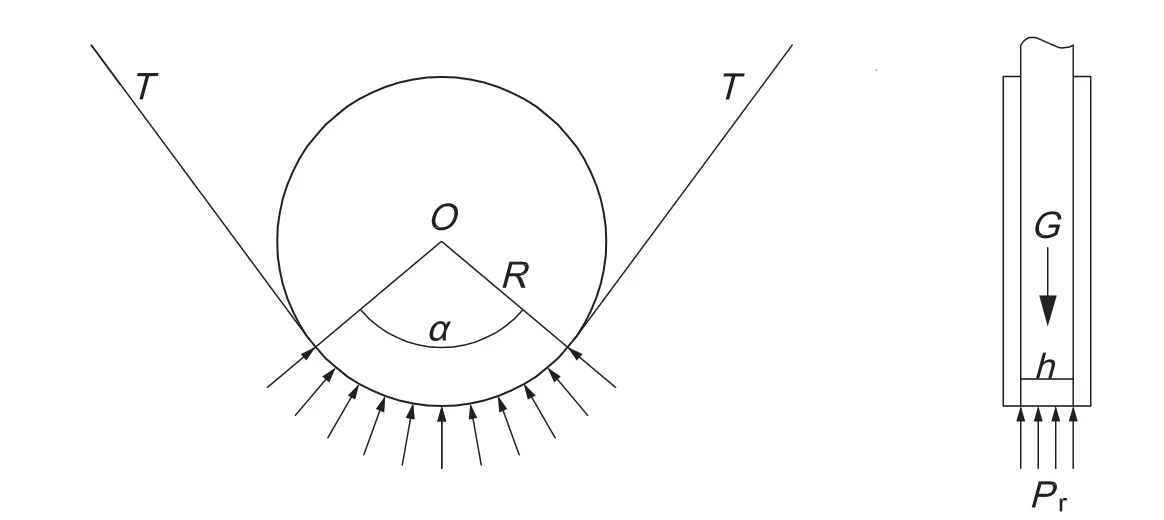
图1 钢带支撑反射镜受力示意图Fig.1 The sketch of steel belt supporting

钢带两端拉力沿反射镜切向方向,大小为:

钢带与反射镜接触区域的径向载荷,方向指向反射镜重心,大小为:

其中,G是反射镜的重力,R是反射镜的半径,α是反射镜与钢带的接触角,h是钢带的宽度.

设定钢带与反射镜的接触角为180°,钢带宽度为60 mm.反射镜重心平面穿过钢带的中心线,避免反射镜出现翻转的意外.忽略钢带与反射镜之间的摩擦力及钢带自身的弯矩和重力,在钢带与反射镜边缘接触区域施加均匀径向载荷.此时反射镜所受到的外力主要来自于自身的重力作用以及钢带对它的均匀载荷[5].

计算得出反射镜镜面上各节点在光轴方向的位移,如图2左图.对计算结果进行网格收敛性分析,以保证计算的准确性.不断加密网格,节点位移逐渐趋近于不变时,说明网格已经收敛,符合有限元分析检验准则.

该镜面节点位移包含了刚体位移和表面畸变两部分.对分析得到的镜面节点坐标进行Zernike多项式拟合并去除刚体位移,得到表面畸变结果,RMS值为4.62 nm.图2右图是镜面拟合后的变形云图.

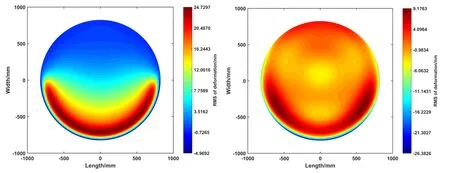
图2 钢带支撑拟合前变形云图(左);钢带支撑拟合后变形云图(右).Fig.2 Deformation contour diagram of steel belt supporting before fitting (left panel);deformation contour diagram of steel belt supporting after fitting (right panel).

4 坦克链支撑

在钢带对反射镜侧支撑安装过程中,因为钢带自身的较大硬度,事实上很难与反射镜侧面完美贴合,会额外引起一些应力,从而影响反射镜的面型精度[5],另外由于镜面加工与检测过程中需要多次拆装钢带,因安装导致的附加应力带来检测结果的不确定性也是难以消除的干扰因素.因此,Vukobratovich和Richard[4]引入了坦克链支撑方案,如图3所示,A–A意为剖面图.反射镜竖直放置,光轴保持水平状态,两条相同规格的坦克链通过螺栓连接固定在镜室上,分别承担反射镜一半的重力,相对于反射镜的重心平面对称布置.与钢带支撑相比,坦克链优点更加显著:降低了接触区域的摩擦力,可以获得更好的面型;可以通过调节坦克链的轴向位置从而降低反射镜倾覆的可能性,空间稳定性更高;坦克链作为成熟的工业产品,市场上可供选择的种类很多、价格便宜,更易于采购使用.选择坦克链支撑的两个重要参数分别为坦克链的节数和中心距,这两个参数对反射镜的面型结果有着直接的影响,在下文展开深入仔细的研究.

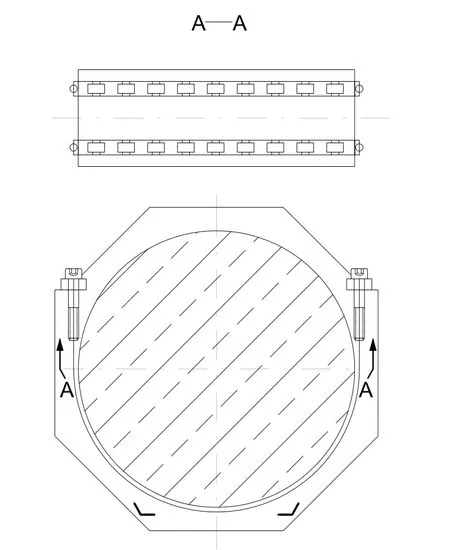
图3 坦克链支撑示意图Fig.3 Illustration of roller-chain supporting

4.1 链节数量分析

坦克链支撑结构的特点在于,坦克链滚子与反射镜的边缘是线接触,区别于钢带支撑的面接触.参考了Fitzsimmons等[6]的均匀径向力模型,每一个坦克链滚子对反射镜的径向力都是大小相等,方向垂直于接触区域并指向反射镜圆心.这些径向力在竖直方向的合力与反射镜的重力平衡.

反射镜在坦克链支撑结构下,首先要确定合理的链节数量.在这里,我们先只考虑链节数量,暂时忽略其他因素.坦克链的链节数量决定了支撑点的数量,从而影响了支撑力的大小与位置,是影响反射镜面型及应力的重要因素.在保证支撑方式安全可靠的情况下,探究不同链节数量对于镜面变形以及应力分布的影响[5].采用了不同链节数量的坦克链对Φ 1650 mm口径反射镜进行侧支撑,分析了坦克链从10节变化到34节时镜面面型的变化情况.暂定的中心距是80 mm,链条滚子宽度是30 mm.得到了链节数量对面型及应力影响的数据,如表2.

表2 链节数量对面型及应力的影响Table 2 Effects of pitches on surface accuracy and stress

图4显示了不同的链节数量对面型及应力的影响.图4左图是链节数量对拟合前后的反射镜面型的影响,图4右图是链节数量对反射镜受到最大应力的影响.从图4左图中可以看出,反射镜的RMS随着链节数量的增加而波动变化,在26节时,拟合后的RMS达到了最小值.根据图4右图,随着链节数量的增加,反射镜的最大等效应力在逐步降低,都处于最大许用应力范围之内,从力学性能角度保证了坦克链支撑结构的可靠性.最终选择了链节数量为26的坦克链进行反射镜的侧支撑.

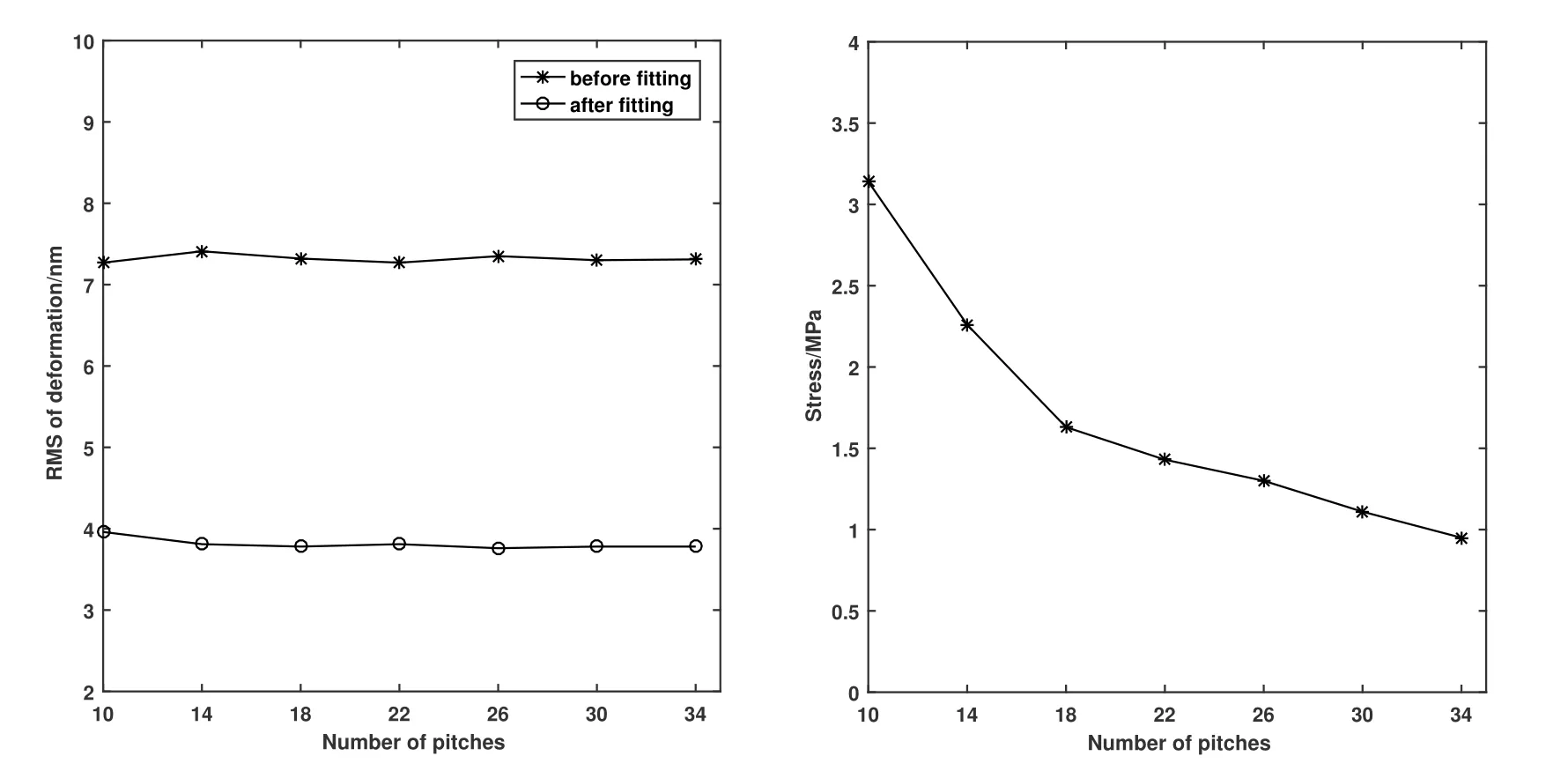
图4 拟合前后链节数量对面型的影响(左);链节数量对最大应力的影响(右).Fig.4 Effects of pitches on surface accuracy before and after fitting (left panel);effects of pitches on stress (right panel).

4.2 中心距分析

我们确定了链节数量为26节,两条坦克链之间的中心距也作为一个主要因素进行考量.探究了中心距从40 mm增加到140 mm时反射镜的面型及应力变化情况,如表3.

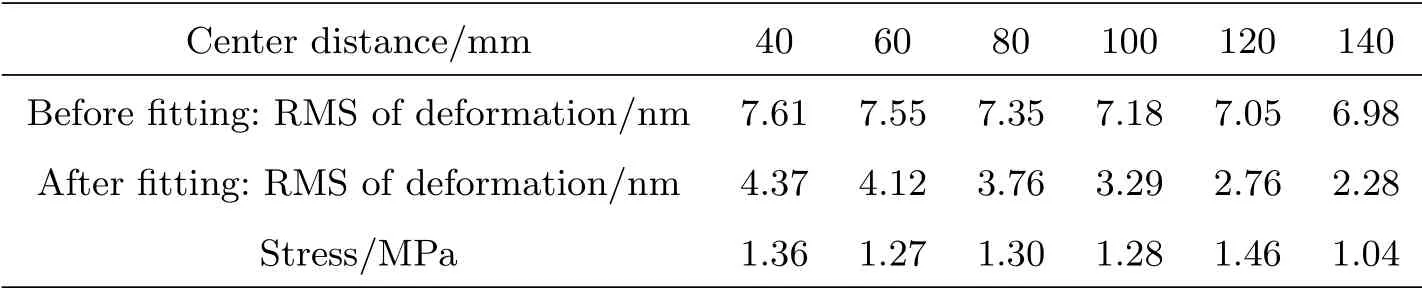
表3 中心距对于面型及应力的影响Table 3 Effects of center distance on surface accuracy and stress

图5反映了坦克链中心距对面型及应力的影响.图5左图是中心距对拟合前后的反射镜面型的影响,图5右图是中心距对反射镜所受最大应力的影响.从图5左图分析,随着中心距的增加,RMS值持续缓慢下降.在中心距为140 mm的时候,拟合前后的RMS值都达到了最小值.图5右图显示,最大应力在一直波动,变化范围不大.综合考虑,确定了中心距为140 mm.

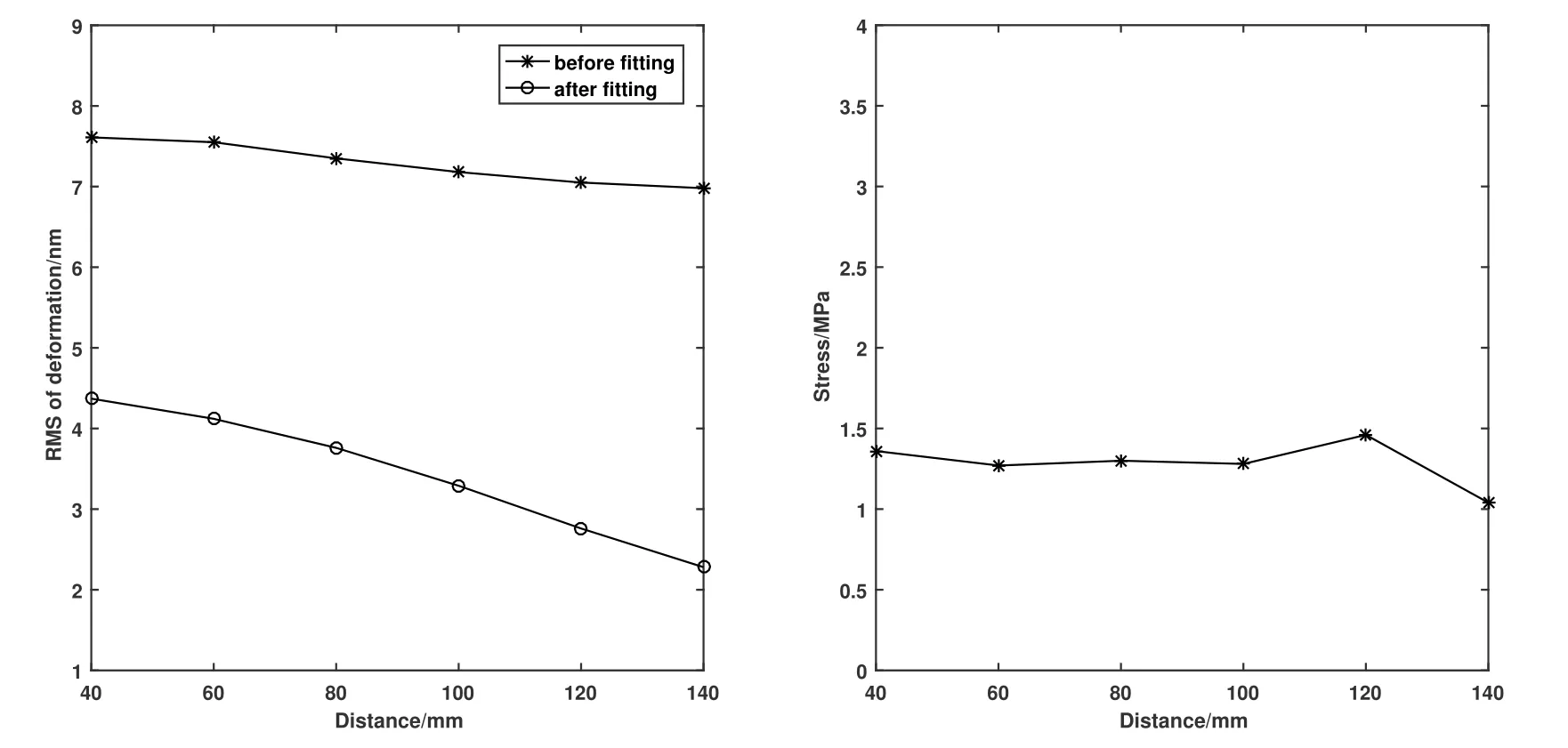
图5 拟合前后中心距对面型的影响(左);中心距对最大应力的影响(右).Fig.5 Effects of center distance on surface accuracy before and after fitting (left panel);effects of center distance on stress (right panel).

除此之外,也对滚子宽度进行了一个初步的仿真,但是从结论来看,滚子宽度变化对面型的影响极不敏感,所以不做专门章节讨论.

5 工艺选型

5.1 选型与计算

综上所述,选用26节、中心距为140 mm的两条坦克链沿着反射镜的重心平面对称布置.查阅标准链条手册[8],选择C2162H大滚子双节距坦克链,节距为101.60 mm (经过计算节数为26),滚子直径为57.15 mm,内节内宽为31.75 mm.

进行有限元仿真时,坦克链与反射镜存在很多约束条件与非线性接触问题,计算复杂且容易不收敛.本文根据赫兹接触理论[9],对坦克链与反射镜的非线性接触进行模型简化,根据公式计算出接触宽度.

滚子与光学元件之间的正压力:

滚子与光学元件的接触长度:

综合曲率半径:

接触区域宽度:

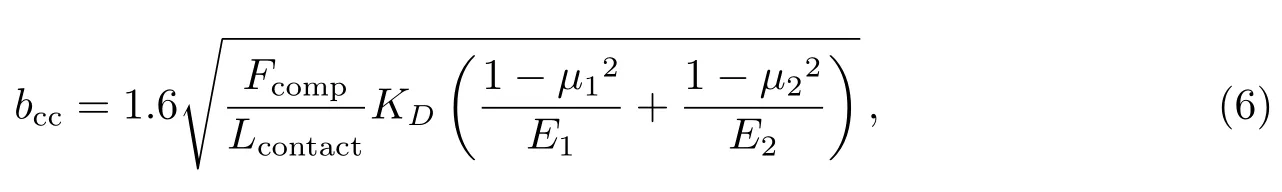
式中,αi是第i节坦克链滚子与反射镜的接触角,D是反射镜的直径,dRC是滚子直径,ωRC是滚子内节内宽,µ1、µ2分别是微晶玻璃和滚子的泊松比,E1、E2分别是微晶玻璃和滚子的杨氏模量.

图6左图是镜面拟合前变形云图,图6右图是Zernike多项式拟合后的变形云图.拟合后的RMS值为2.58 nm,满足预期的技术指标.

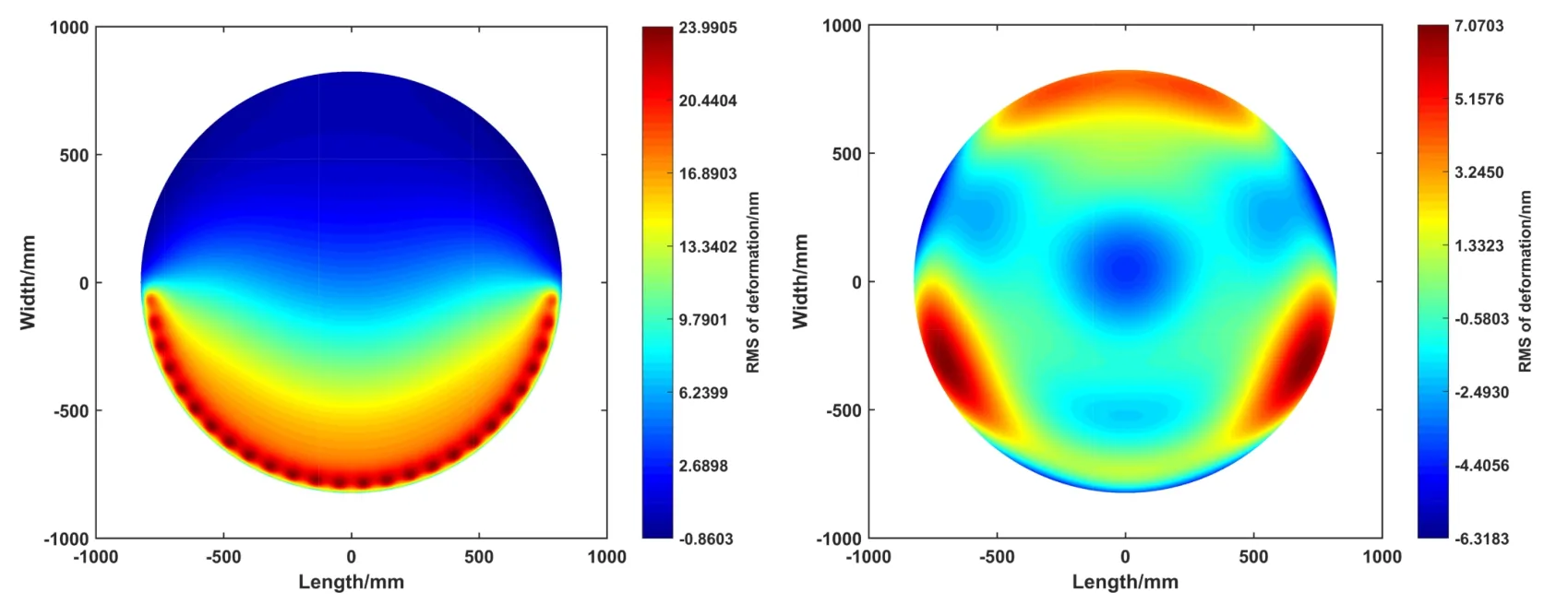
图6 坦克链支撑拟合前变形云图(左);坦克链支撑拟合后变形云图(右).Fig.6 Deformation contour diagram of roller-chain supporting before fitting (left panel);deformation contour diagram of roller-chain supporting after fitting (right panel).