Temperature-dependent Photoluminescence Properties of Cs0.05FA0.79MA0.16PbI2.52Br0.48 Perovskite Thin Film

ZHANG Qiong, WU Yue-jia, FENG Yan-qin, SUN Li-wei, DAI Jun

(School of Science, Jiangsu University of Science and Technology, Zhenjiang 212100, China)

*Corresponding Author, E-mail: daijun@just.edu.cn

Abstract: This paper reports the temperature-dependent photoluminescence properties of Cs0.05FA0.79MA0.16PbI2.52-Br0.48 perovskite thin film. The Cs0.05FA0.79MA0.16PbI2.52Br0.48 perovskite thin film was prepared by one-step spin coating with chlorobenzene anti-solvent treatment, and the surface morphology and crystallization quality were characterized. The X-ray diffraction(XRD) indicates that the Cs0.05FA0.79MA0.16PbI2.52Br0.48 has a typical tetragonal perovskite structure. The perovskite film has a uniform and dense surface, and the grain size is about 300 nm. The photoluminescence intensity was measured in the temperature range of 5-200 K. The photoluminescence spectra show a continuous blue shift of about 9.36 nm, and there is no reversal redshift induced by phase transition. The photoluminescence intensity shows a bi-exponential quenching with the increase of temperature, and two thermal activation energies are obtained by Arrhenius equation. The optical bandgap is fitted by the Bose-Einstein double harmonic oscillator model, and the non-renormalized bandgap energy, the energies of acoustic phonon and optical phonon were fitted. The photoluminescence broadening mechanism was studied by the Segall formula. At 10 K and 100 K, the photoluminescence is mainly from exciton recombination, while at 200 K, the radiation recombination is mainly from free-to-bound and donor-acceptor pairs, which means the defect associated photoluminescence arises at high temperature. The detailed optical parameters in our paper can provide a physical foundation for further optimization of perovskite optoelectronic devices.

Key words: perovskite thin film; photoluminescence; exciton-phonon interaction

1 Introduction

In recent years, with the significant improvement of the performance of organic-inorganic metal halide perovskite solar cells, perovskite semiconductor was regarded as the ideal photovoltaic material to substitute the traditional silicon. Meanwhile, perovskite semiconductor materials also present excellent advantages in the light-emitting diodes, lasers and photodetectors. Therefore, semiconductor perovskite materials attract tremendous attention in the field of optoelectronics. The performance of optoelectronics devices strongly depends on the basic properties of carriers, such as the exciton binding energy, diffusion length, carrier-phonon interaction, and so on. Except for the organic-inorganic halide perovskite MAPbX3[1-2]and pure inorganic perovskite CsPbX3[3-4], scientists found many kinds of multiple cation perovskite CsFAMAPbI3[5]can present higher power conversion efficiency than the MAPbI3and CsPbI3perovskite solar cell[6-9], so the CsFAMAPbI3is widely accepted as the active layer for the solar cell, and the Cs0.05(FA0.83MA0.17)0.95Pb(I0.83Br0.17)3achieves the best efficiency of 20.48%[10]. Usu-ally, the MAPbI3perovskite bandgap changes with temperature, and phase transition can take place at about 120 K[11-13], which leads to the photoluminescence center reversal redshift. However, the temperature-dependent bandgap, photoluminescence profile and the carrier-phonon interaction have not been studied for such mixed cation perovskite CsFAMAPb-(I/Br)3.

In this paper, the optical properties of the Cs0.05FA0.79MA0.16PbI2.52Br0.48perovskite thin film with the reported highest power conversion efficiency was investigated. The Cs0.05FA0.79MA0.16PbI2.52Br0.48thin film was fabricated by spin-coating method, and the X-ray diffraction(XRD) and field-emission scanning electron microscope(FE-SEM) were measured to characterize the structure. The temperature-dependent photoluminescence center wavelength presents continuous blueshift as the temperature changes from 5 K to 200 K. The photoluminescence linewidth presents broadening as the temperature increases. The exciton binding energy, non-renormalization bandgap energy, electron-phonon coupling coefficient, optical and acoustic phonon energy are systematically studied.

2 Experiments

Formamidinium iodide(FAI) and methylammonium bromide(MABr) were bought from Dyesol. Lead iodide(PbI2) and lead bromide(PbBr2) were bought from Sigma-Aldrich. Cesium iodide(CsI) was bought from Alfa Aesar. The perovskite precursor solutions were prepared by dissolving CsI(0.057 mol·L-1), FAI(1.16 mol·L-1), PbI2(1.24 mol·L-1), MABr(0.23 mol·L-1) and PbBr2(0.238 mol·L-1) in the mixed solvent of DMF∶DMSO=4∶1(volume ratio). The solution was stirred at 60 ℃ for 10 h and then filtered through a polytetrafluoroethylene filter(pore diameter 0.22 μm).

Indium-tin oxide glass substrates were sonicated for 15 min with detergent, deionized water, acetone and anhydrous ethanol, respectively. The substrates are dried by nitrogen, then cleaned in the UV-ozone cleaner for 15 min. The cleaned substrates were transferred to a nitrogen glove box. The perovskite precursor solution was spin-coated on ITO substrates with 6 000 r/min for 30 s in a nitrogen glove box, at the 20th second, dip 200 μL chlorobenzene quickly to improve the perovskite crystalline quality. Then the obtained Cs0.05FA0.79MA0.16PbI2.52Br0.48perovskite thin film was annealed at 100 ℃ on the heating plate for 30 min.

Under the irradiation of Cu Kα(λ=0.154 056 nm), XRD of the Cs0.05FA0.79-MA0.16PbI2.52Br0.48thin film was measured by Bruker D8 superior diffractometer, and the morphology of the sample was measured by scanning electron microscope(Zeiss SURRA-40). The sample was positioned in a quartz optical cavity, refrigerated to 5 K through liquid nitrogen cryogenic system(Janis 150c), excited by means of 325 nm laser, then temperature was adjusted from 5 K to 200 K, and the photoluminescence spectra was amassed by means of a spectrometer geared up with CCD(SP 2500i, Acton).

3 Results and Discussion

Fig.1(a) shows SEM image of Cs0.05FA0.79-MA0.16PbI2.52Br0.48perovskite thin film and the scale bar is 3 μm. The complete film is composed of uniform and dense perovskite layer, and the grain size is about 300 nm.

Fig.1 SEM image(a)， AFM image(b) and XRD pattern(c) of Cs0.05FA0.79MA0.16PbI2.52Br0.48 perovskite thin film.

Fig.1(b) shows the AFM image of as-fabricated film with the root mean square roughness of 36.9 nm. Fig.1(c) shows the XRD pattern of Cs0.05-FA0.79MA0.16PbI2.52Br0.48perovskite thin film coated on ITO substrates. In the X-ray diffraction pattern, except for the diffraction from the ITO substrate and PbI2, the other Bragg signals can be assigned to tetragonal perovskite phases. The obvious peak at 12.73° indicates that there is excess lead iodide(PbI2) in the solutions of Cs0.05FA0.79MA0.16PbI2.52-Br0.48precursor and the peaks at 14.16°, 20.06°, 24.61°, 28.49°, 31.88°, 35.33°, 40.68°, 43.2° and 50.31° can be assigned to the scattering from (001),(011),(111),(002),(012),(112),(022),(003) and (222) crystal plane of the layered perovskite[14-17]. The signals of 14.16°, 20.06° and 24.61°(2θCu radiation) were observed from the X-ray diffraction patterns. The PbI2signal is widely presented in the perovskite samples due to the excessive PbI2in the precursor solutions[16,18-19].

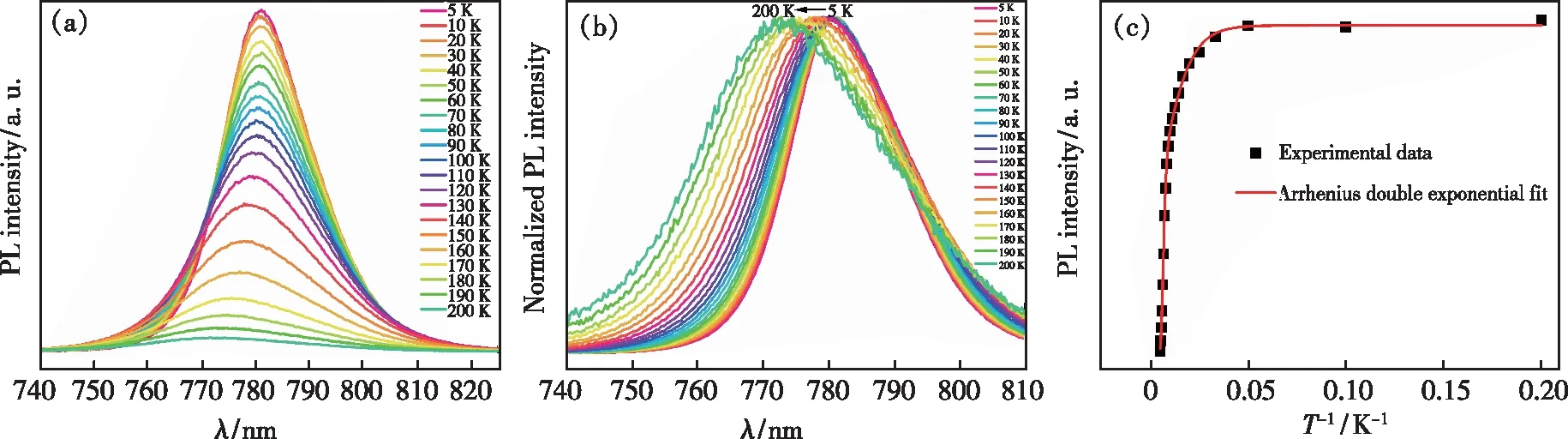
Fig.2 (a)Temperature-dependent photoluminescence spectra of as-fabricated film. (b)Normalized photoluminescence spectra of (a). (c)Rrelationship between photoluminescence intensity and reciprocal of temperature.

The exciton-phonon interaction is examined by measuring the photoluminescence spectra in the temperature vary ofT=5～200 K as proven in Fig.2(a) and (b). Fig.2(a) and (b) show the temperature-dependent unnormalized and normalized photoluminescence spectra of the Cs0.05FA0.79MA0.16PbI2.52-Br0.48perovskite thin film. In addition, a 9.36 nm blueshift of photoluminescence peak position from 781.07 nm to 771.71 nm is observed, and accompanied by a slight broadening of FWHM from 19.4 nm to 34.32 nm. The blueshift reflects the lattice deformation potential and exciton-phonon coupling[20], and it is related to the photoluminescence emission of bound excitons on the short wavelength side. For the pure FAPbI3or MAPbI3, the phase transition temperature is about at 120 K. Here the Cs and Br doping may change the crystal structure[21]. It may be the reason of the absence of phase transition phenomenon.

Fig.2(c) shows the relationship between photoluminescence intensity and reciprocal of temperature, which can be fitted by the Arrhenius equation[22]:

(1)

whereI(T) andI(0) are the emission intensity at the temperaturesTand 0 K,C1andC2are the relative weight of the two quenching processes,kBis Boltzmann constant,E1andE2are the activation energies related with the nonradiative recombination process.E1andE2obtained by fitting are 123.45 meV and 10.73 meV respectively. The highE1is considered as the potential barrier between the localized potential minima and the non-radioactive recombination centers, and the lowE2might be attributed localized exciton binding energy[23-25].

The Bose-Einstein double oscillator model only considers the relative contributions of acoustic phonon and optical phonon, but does not consider the sum of all possible phonon in Brillouin zone, and depends on the fact that the electron-phonon contribution symbols given by the two oscillators are opposite[26]. The model is used to analyze the bandgap change, and described as follows[27]:

(2)

whereE0is non-renormalized bandgap energy,AacandAoptrepresent the relative weight of oscillators (or the electron-phonon coupling coefficients),ωacandωoptare the acoustic and optical phonon energies, andMacandMoptare the relative atomic masses of the oscillator.

Fig.3(a) shows the temperature-dependent bandgap of the Cs0.05FA0.79MA0.16PbI2.52Br0.48perovskite thin film. The model provides an excellent fit(red solid line) to the experimental data obtained for the film across the temperature range studied. The best fitting parameters were obtained asE0=1.639 eV,Aac=3.485,Aopt=-12.99,ωac=50.65 meV andωopt=285.42 meV. The non-renormalized bandgapE0is reasonable, and it is thought between 1.62 eV and 1.65 eV[15,28-29]. As shown in Fig.3(a), the bandgap of Cs0.05FA0.79MA0.16-PbI2.52Br0.48increases non-linearly with the temperature, and the contribution of optical phonon and acoustic phonon to bandgap obeys the Bose-Einstein distribution.

The total photoluminescence emission broadening can be described by the sum of three broadening contributions given by the Segall expression as follows[30]:

Γ(T)=Γinh+ΓAC+ΓLO,

(3)

(4)

whereΓinhis the non-uniform expansion constant caused by exciton-exciton interaction and crystal disorder, which is independent of temperature. In the second term (ΓAC),φACrepresents the phonon coupling coefficient of exciton-phonon interaction, which is mainly related to the temperature-dependent deformation potential interaction. The third term (ΓLO),φLOis the exciton-longitudinal optical phonon coupling coefficient or Fröhlich coupling coefficient, which is related to the Bose-Einstein distribution of LO phonons given as 1/(e(ELO/kT)-1)[26]. Here，ELOis the energy of the LO phonons,kis the Boltzmann constant.

Fig.3(b) shows the temperature-dependent FWHM of the Cs0.05FA0.79MA0.16PbI2.52Br0.48perovskite thin film. The contribution to broadening from acoustic phonon and LO phonon is also plotted. The FHWM

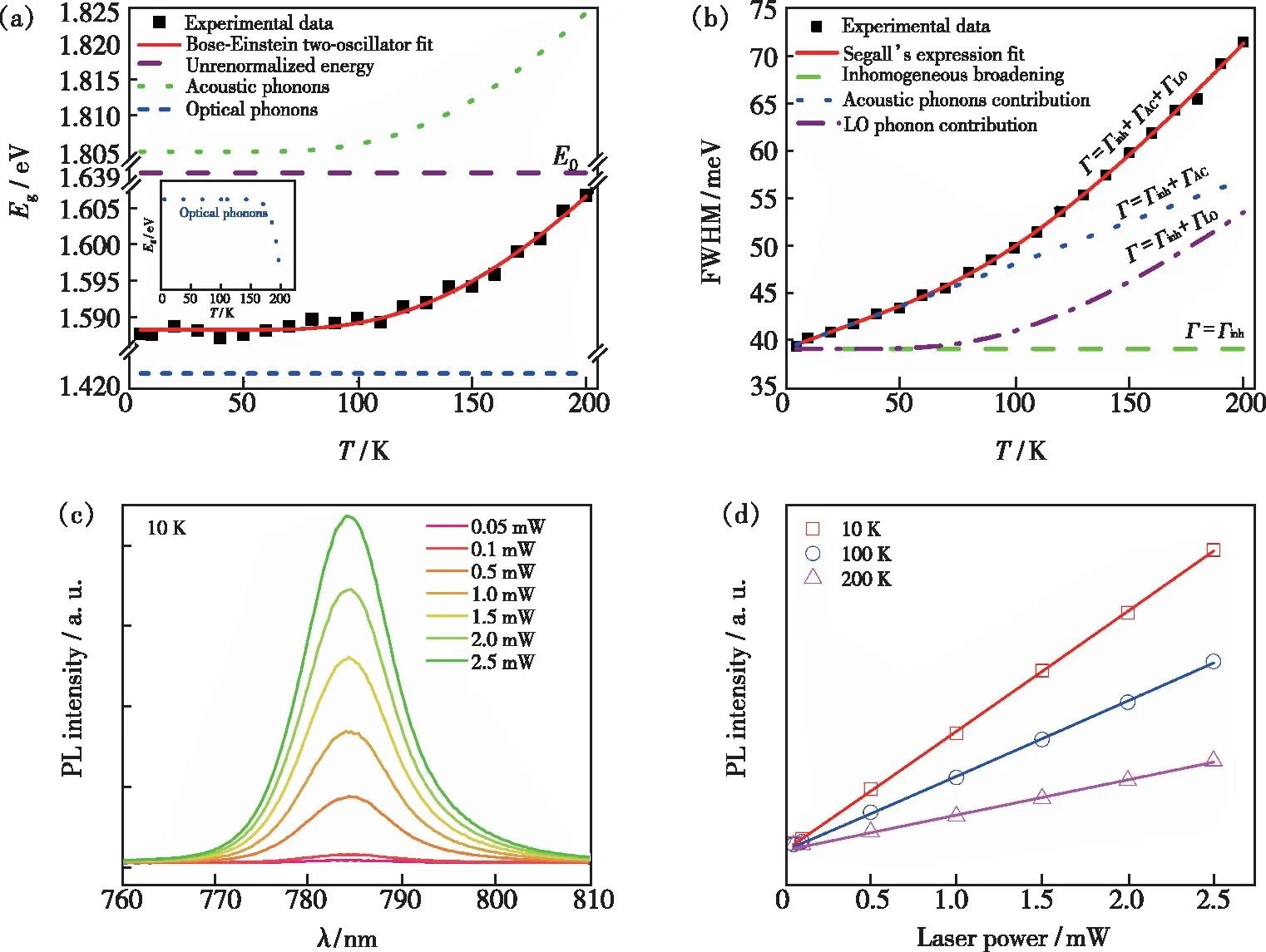
Fig.3 (a)Temperature-dependent photoluminescence bandgap of Cs0.05FA0.79MA0.16PbI2.52Br0.48perovskite thin film. The experimental data(black squares) are fitted using a Bose-Einstein two-oscillator model(red solid line). At the same time, the relative contributions of non-renormalized bandgap energy(horizontal purple dashed line) and lead-like phonon(green dotted line) and X-like optical phonon(blue dotted line) to energy drift are given. (b)Temperature-dependent FWHM for Cs0.05FA0.79MA0.16PbI2.52Br0.48perovskite thin film. The black squares are the experimental data fitted using Segall expression(red solid line). The temperature-dependent the photoluminescence exciton linewidth broadening arising from acoustic phonon interplayΓ(T)=Γinh+ΓAC(blue dash-dot line), LO phonon interplayΓ(T)=Γinh+ΓLO(purple dash-dot line), inhomogeneous broadening termΓ(T)=Γinh(horizontal green dotted line). (c)Photoluminescence spectra evolution with the laser power at 10 K. (d)Relationship between photoluminescence intensity and incident laser power at 10, 100， 200 K.

broadening by the contribution of acoustic phonon increases linearly with the temperature, while LO phonon is on the contrary. It indicates the strong exciton-phonon interactions in Cs0.05FA0.79MA0.16-PbI2.52Br0.48perovskite thin film. The best fitted parameters by equation (4) areΓinh=39.19 meV,φAC=88.93 μeV·K-1,φLO=81.67 meV andELO=32.77 meV.

With the increase of laser power at 10 K, there is no blueshift or redshift in photoluminescence spectra as shown in Fig.3(c). Fig.3(d) shows the relationship between excitation power and photoluminescence intensity at 10， 100， 200 K. The photoluminescence intensityIexponentially increasing with excitation powerPcould be expressed as

I∝Pγ,

(5)

here the parameterγcan reflect the carrier recombination processes physically. Ifγ=1, it indicates that the radiation recombination is dominant[31]. If 1<γ<2, the photoluminescence is mainly from exciton-like recombination, and ifγ<1, the photoluminescence might be from free-to-bound and donor-acceptor pairs recombination[4]. Here the fittedγare 1.006 3 and 1.013 2 at 10 K and 100 K, respectively, which means the photoluminescence is from exciton recombination. While the fittedγ=0.998 6 at 200 K indicates the radiation recombination is mainly from free-to-bound and donor-acceptor pairs, which means the defect associated photoluminescence arises at high temperature[31].

4 Conclusion

In this paper, the temperature-dependent photoluminescence properties of Cs0.05FA0.79MA0.16PbI2.52-Br0.48perovskite thin film treated with chlorobenzene were studied. The temperature-dependent photoluminescence reveals the effect of exciton-phonon coupling. With the increase of temperature, the photoluminescence shows blue-shift and bi-exponential quenching. The activation energiesE1andE2fitted by Arrhenius equation are 123.45 meV and 10.73 meV respectively. The bandgap fitted by the Bose-Einstein double harmonic oscillator model gives the non-renormalized bandgap energy 1.639 eV, and the non-uniform expansion and exciton-phonon coupling coefficients of the photoluminescence were obtained by Segall expression fitting. At 10 K and 100 K, the photoluminescence of Cs0.05FA0.79MA0.16PbI2.52Br0.48is dominated by the exciton recombination, while at 200 K, the photoluminescence is donated by free-to-bound and donor-acceptor pairs, which indicates that the photoluminescence related to defects is produced at high temperature.

Response Letter is available for this paper at：http://cjl.lightpublishing.cn/thesisDetails#10.37188/CJL.20210195.