基于Code Composer Studio的无限冲激响应滤波器(IIR)的设计*
2021-10-09许志敏魏海峰陆彦如
许志敏 魏海峰 陆彦如
(江苏科技大学电子信息学院 镇江 212003)
1 引言
数字信号处理技术伴随着信息科学的发展而迅速发展,滤波器在数字信号处理中基础而又十分重要。数字滤波器通过数值计算实现滤波,其工作稳定、体积小、重量轻、灵活、处理精度高,并且可通过模拟信号和数字信号相互转换的技术来处理模拟信号,这些优点使其广泛应用于语音图像处理、数字通信、频谱分析、模式识别、自动控制等领域,成为数字信号处理中最重要的组成部分之一。
数学信号处理器的出现彻底改变了通信,其具有高速灵活性、可编程性和低消耗等特点,让其在图形、图像处理和语音处理等方面发挥着重要作用。数字信号处理器是一个专用处理器,在模拟信号转换为数字信号后执行高速实时处理,处理速度比CPU快10~50倍。在数字化时代背景下,DSP已经成为通信、计算机、消费类电子产品等领域的基本组成部分。
有限冲激响应滤波器(FIR)和无限冲激响应滤波器(IIR)是常用的两种数字滤波器,无限冲激响应滤波器(IIR)相较于有限冲激响应滤波器(FIR),实现算法更为复杂。但是IIR滤波器工作量相对小,可以用低阶数来实现较高性能要求,所需的存储单元少,从而运行效率得到提高,更加经济。
文献[1]实现了IIR数字滤波器在Matlab中的仿真。文献[2]介绍了后向差分法和双线性变换法,以实现模拟控制器的离散化,本文将采用双线性变换法。文献[3]提出了四种典型的归一化模拟器实现方法,并在Matlab进行仿真实验。文献[4]提出冲激响应不变法会带来的频谱混叠失真问题,“数字-数字频带变化”设计的数字滤波器是一种有效的抗混叠的设计办法。文献[5]在DSPTMS320C54x芯片上实现了FIR低通滤波器。文献[6]用AT89C51合成脉冲波形。文献[7]在DSPTMS320C55x实现IIR数字滤波器。文献[8]通过FPGA实现IIR数字滤波器。文献[9~10]说明滤波器在语音信号处理中的实际应用。文献[11]设计基于Delphi环境实现了IIR滤波器。文献[12~16]、[18]研究了数字滤波器的参数设定、优化等问题。文献[17]设计了基于FPGA的FIR数字带通滤波器。
结合上述文献,本文将采用双线性变换法来设计巴特沃斯滤波器,并在DSP集成开发环境CCS上进行仿真实验。
2 双线性变换法
脉冲响应不变法和双线性变换法是设计IIR数字滤波器的两种常用方法,脉冲响应不变法无法有效解决频谱混淆的问题。因此,本文采用双线性变换法设计IIR数字低通滤波器。
设过渡模拟滤波器的系统函数用Ha(s),s=jΩ,将Ha(s)的复数自变量压缩到±π/T得到系统函数用Ha(s1),s=jΩ1表示,用正切变换频率进行压缩,实现了s平面上整个虚轴完全压缩到s1平面上虚轴的±π/T之间,得到
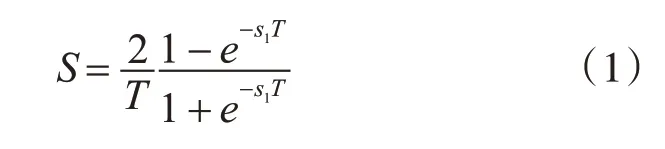
再按照Z=es1T从s1平面转换到z平面变换成Ha(z),得到
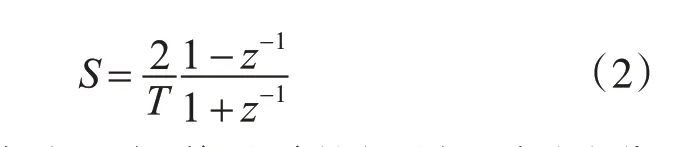
此时便不会出现频谱混淆的问题。式(2)分子、分母函数均是线性的,称为双线性变换。
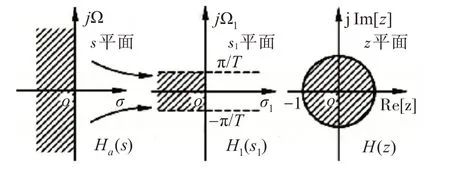
图1 双线性变换过程示意图
3 模拟滤波器设计步骤
1)本系统的设计技术指标为
通带边缘频率fp1、待求阻带边缘频率fs1和待求阻带衰减-20 logδsdB。
模拟边缘频率为fp1=1000Hz,fs1=12000Hz阻带边缘衰减为-20 logδs=30dB
2)将数字低通滤波器的技术指标转换成模拟低通滤波器的技术指标。
用非线性关系Ω1=2πf/fs将待求边缘频率转换成用弧度表示,得到Ωp1和Ωs1。

3)由于双线性变换会出现频率变换非线性,所以预扭曲模拟频率来避免非线性引起的失真。由w=2fstan(Ω/2)求得wp1和ws1,单位为弧度/秒。
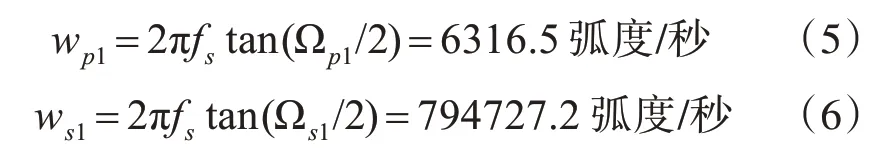
4)根据所需要的阻带衰减-20 logδs来计算出阻带边缘增益δs。
因为-20 logδs=30,所以logδs=-30/20,δs=0.03162。
利用结束计算公式求模拟滤波器的最低阶数:
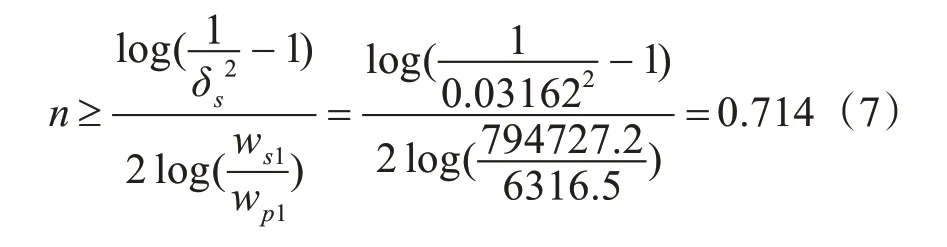
因此,一阶巴特沃斯滤波便可达到要求,完成所需的性能指标。
一阶巴特沃斯滤波器系统传输函数为
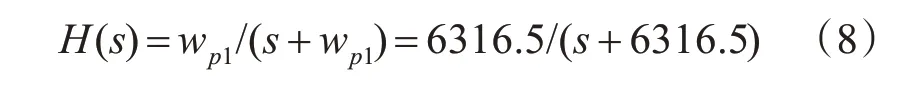
通过双线性变换式(2)得到数字滤波器系统传输函数为
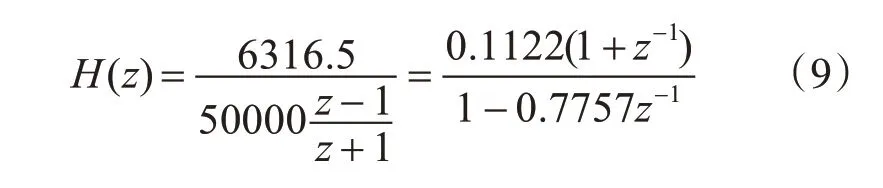
因此系统差分方程为
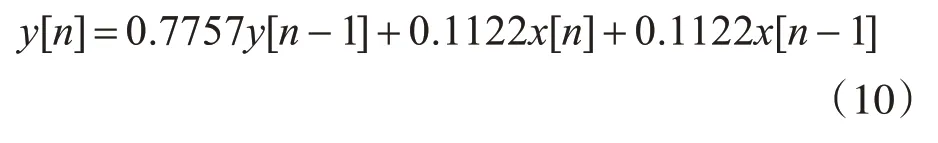
4 IIR滤波器的实现
软件设计分为两大部分,波形产生子程序和无限冲激响应滤波器子程序,采用了C语言与汇编语言相合的方式,在开发环境方面,采用的是DSP集成开发环境Code Composer Studio(CCS)。
1)主程序模块设计如图2所示。
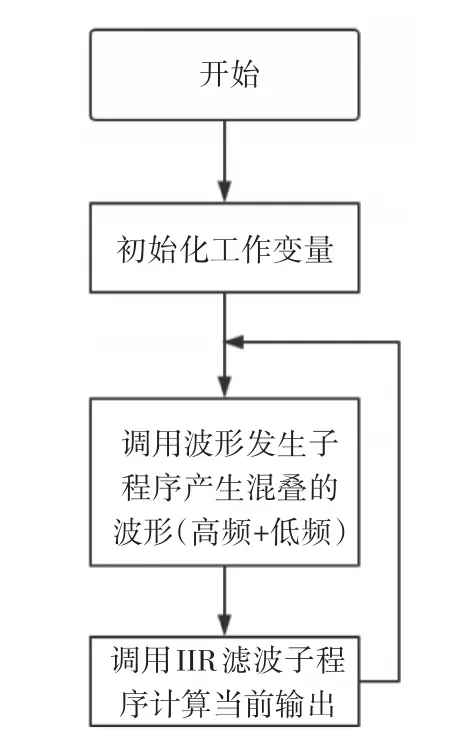
图2 主程序模块设计流程图
2)波形产生子程序设计如图3所示。
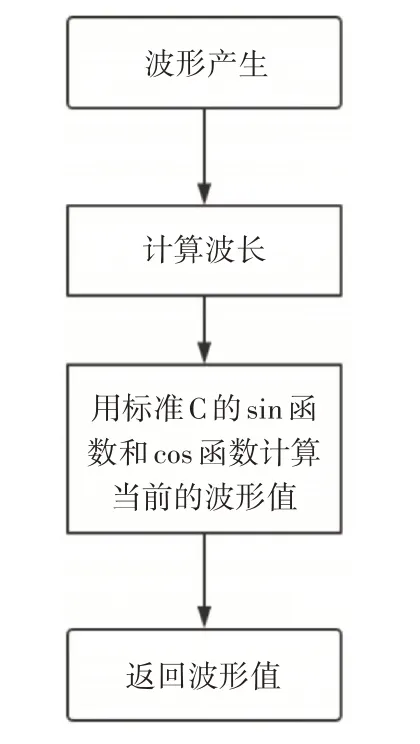
图3 波形产生子程序流程图
3)无限冲激响应滤波器(IIR)子程序设计如图4所示。
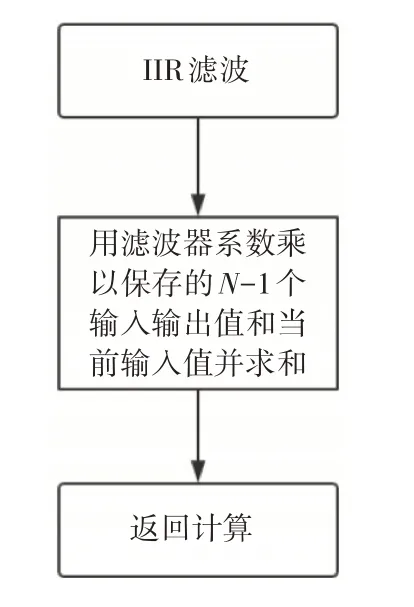
图4 无限冲激响应滤波器(IIR)子程序流程图
5 IIR滤波器的实现
软件调试结果如图5、6所示。
输入波形是低频正弦波和高频余弦波的叠加。
由图5所示的时域仿真结果可以看出:当低频正弦波和高频余弦波相互叠加的信号进入滤波器后,观察输出波形,高频部分的余弦波受到遏制作用而衰减,低频部分的正弦波信号得到保留。
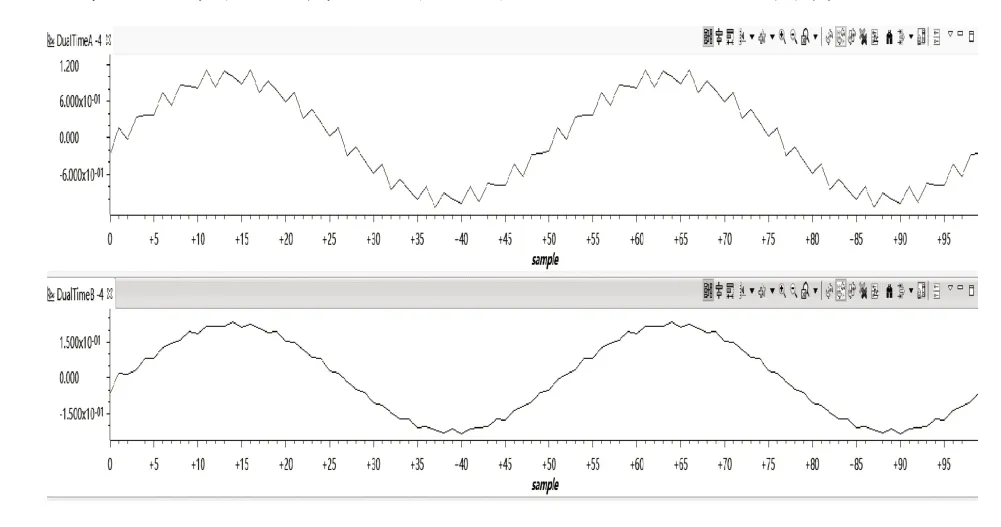
图5 时域仿真结果
结合图6所示的频域仿真结果可以更显著地看出:低频部分(横坐标为0~0.1)的波形无明显变化,而高频部分(横坐标为0.4附近)的波形幅值减小,表明高频部分的波形受到明显的遏制作用。
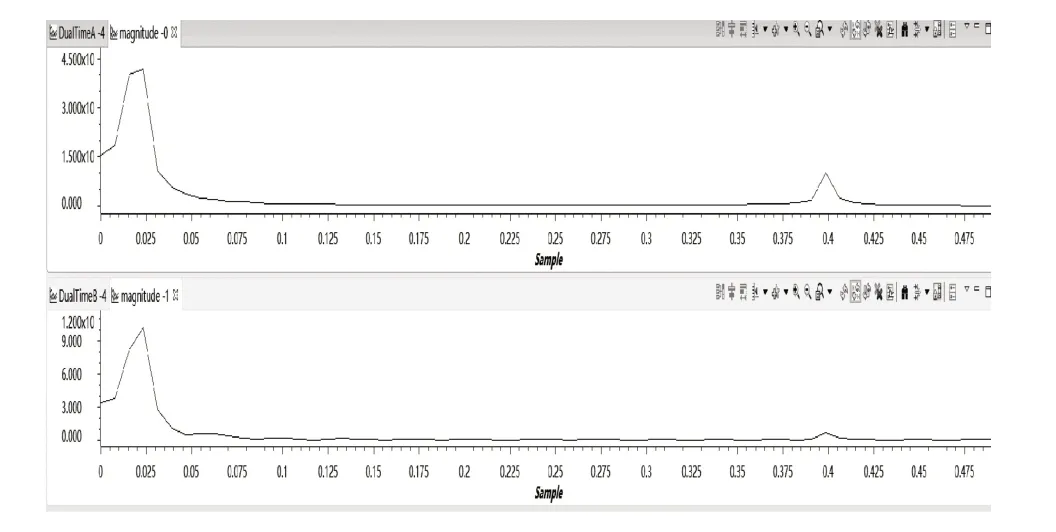
图6 频域仿真结果
6 结语
本文采用CCS集成开发环境软件设计双线性变换法的IIR数字低通滤波器,当输入波形是低频的正弦波和高频的余弦波叠加时,通过观察频域和时域的仿真结果图,得知:当低频正弦波和高频余弦波相互叠加的信号进入滤波器后,高频部分的余弦波收到遏制作用而衰减,低频部分的正弦波信号得到保留。通过无限冲激响应低通滤波器,可以准确地过滤掉输入波形中的高频部分,显示输入波形中的低频部分。
本文简要说明了数字滤波器在数字信号处理的重要作用、数字信号处理器在通信方面的重要地位,分析了有限冲激响应滤波器(FIR)和无限冲激响应滤波器(IIR)的优劣,通过巴特沃斯数字低通滤波器的实例,阐述了双线性变换法的设计步骤,通过仿真结果得出:IIR数字低通滤波器可以准确过滤掉输入信号中的高频部分,显示输入波形中的低频部分。
