HUFFMAN编码技术应用研究

徐爱芸

摘要：现代社会每天产生海量级的信息，而这些信息的存储和传输需要大量的存储空间，信息本身有很大的的冗余度，因此信息必须采用压缩技术处理。Huffman编码是一种流行而又高效的无损编码，利用Huffman编码就可能比普通的编码方法使用的码数少，提高了编码的有效性。

关键词：Huffman编码;最优二叉树;无损压缩

Huffman编码根据消息出现概率的分布特性进行统计，寻找概率与码字长度间的最优匹配，利用数据的统计冗余进行压缩，基于符号出现概率的不同赋予长短不一的码字，出现概率越大的符号，相应的码越短;出现概率越小的符号，其码越长。算法用一串二进制位（称作位码）来代替每个字符，再将这些位码写进压缩后的文件。利用位码压缩的关键之处是选择最优二叉树，在Huffman树中没有一个位码是另一个位码的前缀，每一个字符都在树的叶子结点中出现。

Huffman编码一般用来压缩多媒体信息，如文本、程序文件和特色的图像等，实现对数据的无损压缩。解码时，在消息和码字之间找到明确的一一对应关系，恢复时能准确无误地再现出来，完全恢复原始数据而不引起任何失真。

1编码步骤

Huffman编码是一种一致性编码法，以Huffman树即带权路径长度最小的二叉树构建变长最佳编码，其步骤如下：

（1）将信源符号按其出现的概率，由大到小顺序排列;

（2）将两个最小的概率的信源符号进行组合相加，并重复这一步骤，始终将较大的概率分支放在上部，直到只剩下一个信源符号且概率达到1.0为止;

（3）对每对组合的上边一个指定为1，下边一个指定为0;

（4）画出由每个信源符号到概率1处的路径，记下沿路径的1和0;

（5）对于每个信源符号都写出1、0序列，就得到非等长的Huffman码。

2 Huffman编码设计

例如要压缩字符串“abaadffbghadffda”，首先统计各字符出现的概率：

a： 5/16，b：2 /16，d：3 /16，f： 4/16，g： 1/16，h：1/16

上述原字符的二進制编码为 ： 01100001 01100010 01100001 01100001 01100100 01100110 01100110 01100010 01100111 01101000 01100001 01100100 01100110 01100110 01100100 01100001，共128bit。

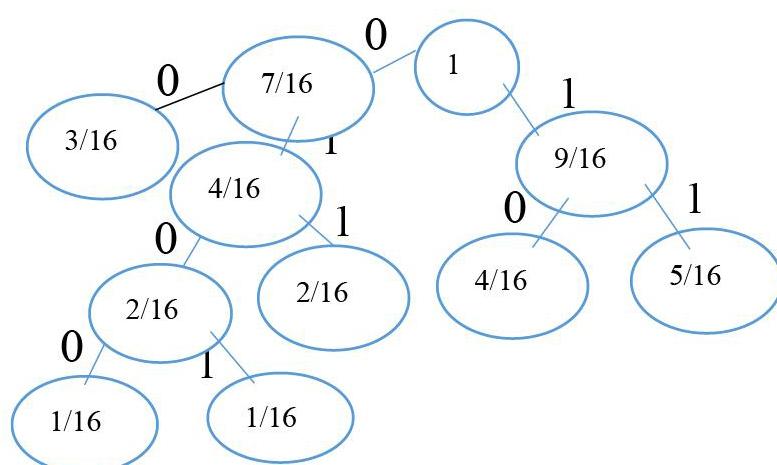
构造Huffman树，树从最下层的结点开始构造，选取概率最小和次小的两个符号作为左右子树构造一棵新的二叉树，新二叉树根结点的权值为其左右子树根结点权值之和。重复这一过程，最后得到一个横放的码树即Huffman树。

Huffman编码就是将从根结点出发到叶结点的路径上各左、右分支的编码顺序排列就得到了该叶子结点所对应的字符的二进制前缀编码，每个字符转换为一个唯一的二进制位串，则该字符串中每个字符的Huffman编码为： a：11，b：011，d：00，f： 10，g： 0100，h：0101

原字符串的Huffman编码为：11 011 11 11 00 10 10 011 0100 0101 11 00 10 10 00 11，共38bit。

3 Huffman编码分析

（1）压缩比

压缩比是压缩前后所需的信息存储量之比，上面的例子中可以计算出压缩比为：38/128=30%，所以说Huffman编码在数据压缩中的压缩效果是非常好的，只要Huffman编码表基于大量概率统计，其编码效果是足够好的。

（2）时间空间效率高

Huffman编码是最佳变长码，得到的是最短的编码长度，有效节省空间。

（3）Huffman编码是无失真的数据压缩编码，解码之后可以无失真的恢复原信息。

（4）Huffman编码的实现方法有很多，比如说MATLAB实现，C语言实现等。

4 Huffman编码不足

（1）Huffman编码要精确统计出每个符号出现的概率，通常要进行两次扫描：第一遍扫描产生统计结果，第二次扫描完成编码，所以编码速度相对慢。

（2）Huffman编码只能用整数来表示单个符号而不能用小数。

（3）只有当信息源各符号出现的概率很不平均的时候，霍夫曼编码的效果才明显。

（4）哈夫曼方法构造出来的码不是唯一的。

5译码

解码时，将码字用码值代替。解码时必须参照这一Huffman编码表才能正确译码，所以在信源的存储与传输过程中必须首先存储或传输这一Huffman编码表。

结束语

Huffman编码是最佳变长码，编码的效率高，它依赖于信源的统计特性，如果消息数很大，需要存储的码表也要很大，会影响存储量、编码以及译码速度等性能。

参考文献

[1]孟彩霞.计算机软件基础，西安电子科技大学出版社，2015.1.

[2]李忠月.数据结构与算法（C语言版）.北京大学出版社，2019.3.