装配式双钢套管混凝土组合剪力墙抗震性能有限元分析

2021-10-08黄明壕黄炎生

华南地震 2021年3期

黄明壕，黄炎生，熊枫

（华南理工大学土木与交通学院，广州 510640）

0 引言

预制装配式建筑因为工业化生产、现场湿作业少和绿色节能等优点成为当前高层建筑发展的趋势。剪力墙作为高层建筑的重要受力构件，其装配化是研究装配式高层建筑的重要课题。混凝土高层建筑对装配式结构要求“等同现浇”的性能，以保证结构具有良好的整体性。现有装配式混凝土剪力墙的力学性能依赖竖向钢筋连接的构造和施工质量，构造复杂、施工要求高、质量控制难度大。钢管混凝土剪力墙是近十几年来发展起来的具有较高承载力和抗震性能的组合剪力墙形式，大量试验[1-5]研究表明钢管混凝土组合剪力墙试件具有高承载力、刚度退化慢、抗震性能好的优点，即使在高轴压比下试件仍有良好的延性能力。

周靖[6]等提出一种新型的装配式内置双钢套管混凝土组合剪力墙，熊枫等[7]依据此组合剪力墙（下文都用此简称）设计了SW1～SW6六个试件进行加载试验。该组合剪力墙采用“部分装配、部分现浇”的复合方式。“部分装配”为内置外钢管的预制混凝土剪力墙，“部分现浇”为内钢管高强混凝土柱芯。内钢管高强混凝土柱芯作为连续无削弱地贯穿不同层剪力墙的主体部件，既是装配时的定位构件，也是受力时抗压、抗弯、抗剪的受力构件。在剪力墙装配时，预制剪力墙通过内置外钢管管孔套装内钢管的方式进行定位组装，剪力墙间外钢管采用焊接形式连接，内外钢管采用径向螺栓连接。试件设计轴压比的受压情况和底端固定、上端位移约束的约束条件模拟组合剪力墙在建筑底层遭遇地震时的受力状态；设计两层剪力墙检验组合剪力墙在载荷状态下装配模式和连接方式是否能达到装配整体性要求。结果证明这种组合剪力墙既具有钢管剪力墙高承载力、抗震性能好的优点，又具有整体性好、装配方便的优势。

试验发现组合剪力墙含圆钢率小的试件具有更好的位移延性，可通过改变含圆钢率对组合剪力墙进行优化。但受限于实际试验的条件，未能对该现象进行更加深入的研究。为研究组合剪力墙不同含圆钢率对其抗震性能的影响，本文在前期试验研究的基础上，基于有限元软件ABAQUS对装配式内置双钢套管混凝土组合剪力墙进行拟合分析。建立不同含圆钢率的有限元模型进行加载，对结果对比分析，以期发现含圆钢率对组合剪力墙抗震性能影响的规律。

1 有限元模型

本文先以SW1试件参数进行建模，采用分离式方法分别建立钢管、钢筋、钢管内混凝土和钢管外混凝土部件，再将各部件组建在一起并通过定义接触关系使各部件组合成一个整体，最后通过定义边界条件和加载方式使有限元分析符合实际试验情况。

1.1 几何尺寸

有限元模型依据试验SW1试件进行等参数建模，模型的几何尺寸相同。截面尺寸和配筋如图1所示。

图1 试件的尺寸及钢筋构造Fig.1 Dimensions and reinforcement details of specimens

1.2 材料本构模型

混凝土材料与钢筋的材料力学性能采用熊枫等试验[7]的实测数据，如表1和表2所示：

表1 混凝土力学性能Table1 Material propertiesof concrete

表2 钢筋和钢管的力学性能Table2 Material propertiesfor reinforcing bars and steel tubes

混凝土采用ABAQUS中的塑性损伤模型（Concrete damaged plasticity model），CDP模型考虑了混凝土在受荷过程中的损伤，能很好拟合模型在加载后期的混凝土损伤情况。其中钢管外混凝土的单轴受压/受拉应力-应变关系采用《混凝土结构设计规范》（GB 50010-2010）中附录C[8]所提供的混凝土本构关系模型。核心混凝土处于钢管内，在高轴压比的水平位移加载下处于三轴受压的复杂应力状态，材料力学性能与钢管外混凝土有较大的差异，单轴受压应力-应变关系采用韩林海等[9]在文献中介绍的适用于钢管混凝土的核心混凝土本构关系模型，模型公式计算如下：

式中的应变单位为με，其中，ξ为混凝土的约束特征系数，它的取值与核心混凝土和钢管的截面面积和屈服极限有关。

钢管外混凝土和核心混凝土受压本构模型见图2。

图2 混凝土受压本构模型Fig.2 Constitutive model of concrete under compression

CDP模型中的损伤因子采用刘巍等[10]建议的方法计算而得，损伤因子计算公式的比例系数ηc和ηt分别取0.6和0.9，刚度恢复因子wc和wt默认缺省值1和0。混凝土材料其余参数见表3：

表3 其余参数取值Table 3 Value of remaining parameters

钢筋采用双斜线模型，考虑到试验采用20#无缝钢管，属于流幅较长的低强度钢材，且通过试验结果可知，边缘钢管最大应变约为0.004，故钢管采用完全弹塑性的双直线模型。

1.3 单元选取

考虑到混凝土自身的材料特性，混凝土采用C3D8R单元，即三维实体8节点减缩积分单位；对于钢管采用壳单元与实体单元计算的结果误差很小，但钢管在采用壳单元时接触定义比采用实体单元相对更加复杂且计算量大，因此钢管采用C3D8R，即三维实体8节点减缩积分单位；考虑到钢筋只承受拉压荷载的受力特点，故钢筋采用T3D2单元，即三维桁架2节点完全积分单元。

1.4 接触关系

由试验可知，一二层的钢管焊接连接可有效传递剪力，内外钢管可通过螺栓有效传递水平荷载，故将内外钢管合并成一根贯通一二层的钢管。钢管与管内、管外的混凝土接触关系均采用Tie约束模拟。钢筋与混凝土的接触关系采用Embedded嵌入单元。由试验结果可知，钢管剪力墙与加载梁和底梁连接良好，没有发生水平错动，故采用Tie约束定义三者之间相互作用关系。

1.5 边界条件与加载方式

试验中试件通过地梁锚栓固定在工作台上，二层加载梁采用位移控制的加载方式，一二层剪力墙按F1：F2=1：2施加水平荷载，在墙顶施加竖向力。在有限元模拟中，剪力墙的底端采用固定约束的边界条件，二层加载梁顶部施加轴向荷载，荷载大小参照《组合结构设计规范》[11]。二层加载梁施加以位移控制的水平荷载，大小为45 mm，在一层加载梁施加水平力，荷载数值依据试验实际采集数据。试件的有限元模型见图3。

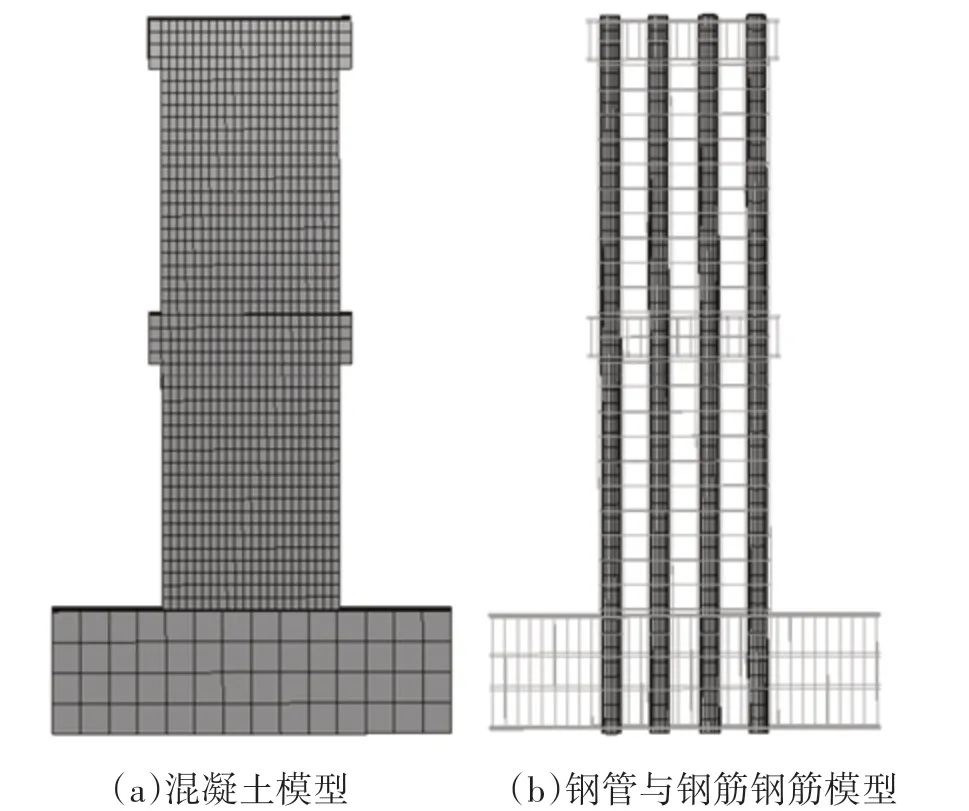
图3 试件模型Fig.3 Specimensmodel

2 有限元分析

验证有限元模型的合理性，进行SW1有限元分析并与试验结果对比，验证模型的合理性，再依据SW2～SW6试件参数建立多组模型进一步分析，验证合理性并获得试验一致性结论。在已验证的模型基础上建立多个不同含圆钢率的模型，进一步研究含圆钢率对组合剪力墙抗震性能的影响。考虑到模拟试件在特定工况下的全过程滞回曲线计算量较大，而构件在单调加载制度下的荷载-位移曲线能够近似反应低周往复荷载作用下的承载力骨架曲线，所以本文仅采用水平单推作用加载方式对有限元模型模拟分析。

2.1 有限元结果验证

对SW1试件进行有限元分析并与试验结果数据的骨架曲线进行对比，结果见图4。

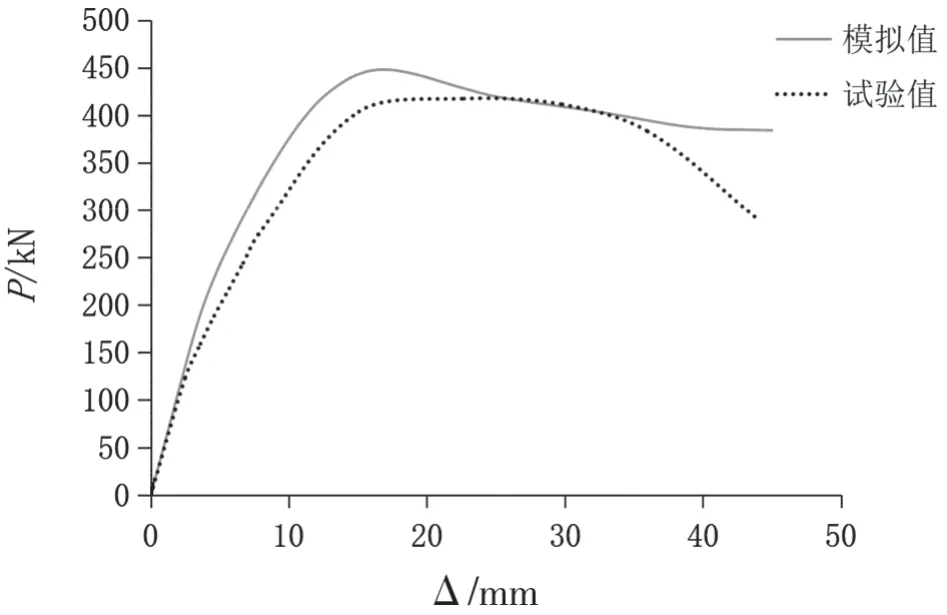
图4 SW1荷载—位移曲线对比Fig.4 SW1 load-displacement comparison curve

由图4可知，有限元分析结果和试验结果具有较好的吻合度，有限元峰值承载力为447.8 kN，与试验值417.3 kN误差为7.3%，小于10%。基于已验证的SW1有限元模型，依据实际试验的其余SW2～SW6试件参数，建立SW2～SW4、SW6四个有限元模型，参数见表4。将模型进行计算分析并与试验结果进行对比，结果见图5。

表4 试件参数Table 4 Design parametersof specimens

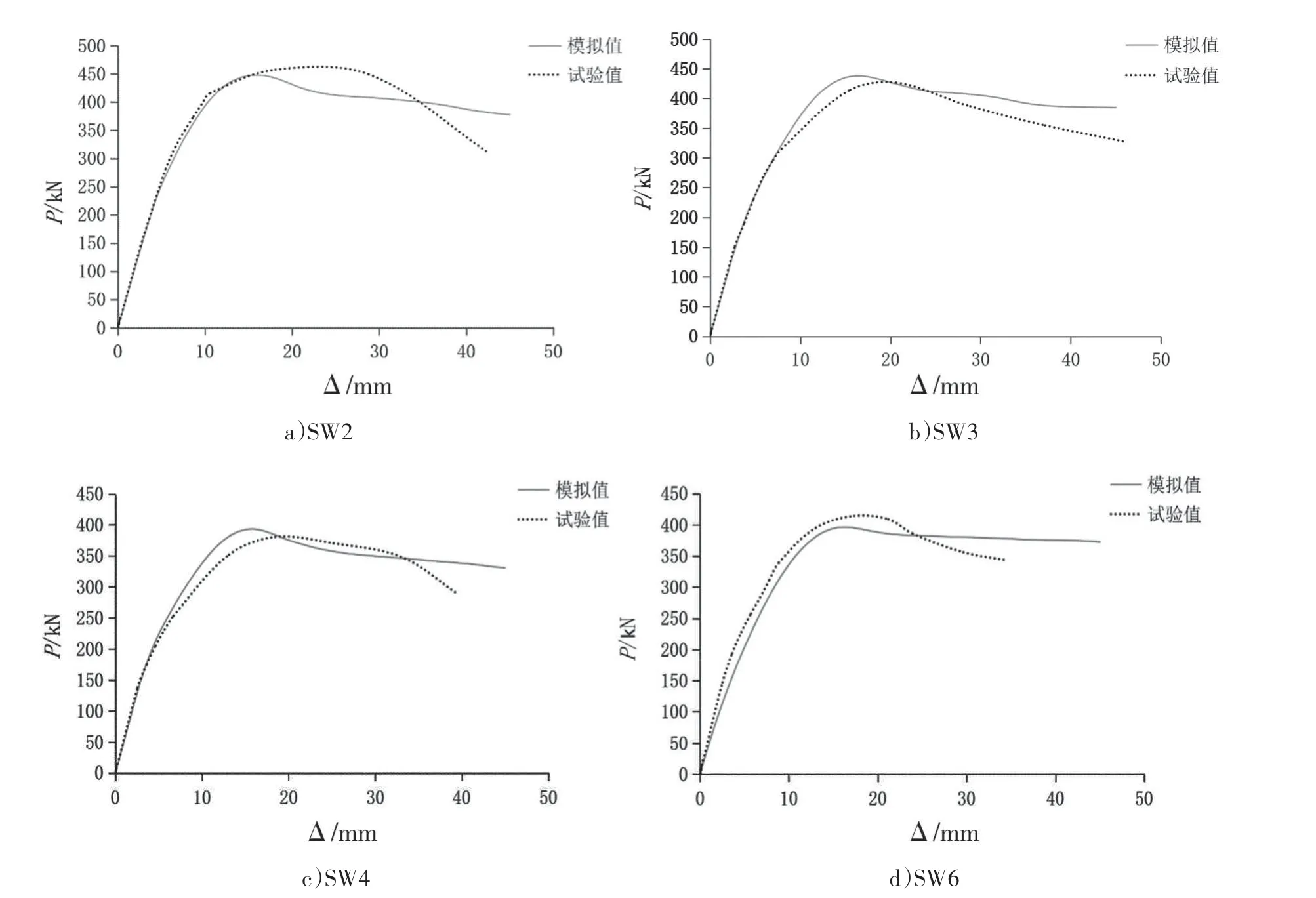
图5 模拟值和试验值荷载—位移曲线对比Fig.5 Comparison of simulated and tested load-displacement curves

2.2 结果对比分析

由图5可知，有限元模拟所得的荷载-位移曲线与试验中提取所得荷载-位移曲线吻合较好。两者的承载力峰值相差不大，误差均在10%以内，试件承载力的模拟值与试验所得的实际值见表5。模拟值在加载后期均有下降段，但均未能模拟出试件在达到峰值之后承载力的较大下降段，这主要是软件中采用的混凝土本构模型无法模拟混凝土加载后期真实压碎、开裂情况和钢管、钢筋与混凝土界面滑移情况。有限元模拟获得与试验一致性结果，反向证明试验结果的准确性。

表5 承载力模拟值与试验值对比Table5 Comparison of simulated and experimental values of bearing capacity

2.3 含圆钢率参数分析

试验研究发现含圆钢率低的试件具有更好的延性，但因实际试验条件的限制，未能深入研究含圆钢率对组合剪力墙抗震性能的影响规律与工作机理。为进一步研究含圆钢率对组合剪力墙抗震性能的影响，本文以已验证合理性的SW1有限元模型为基础，通过控制单一变量，建立5个不同含圆钢率的组合剪力墙有限元模型进行模拟分析，对模型进行水平单推作用加载分析，计算模型参数见表6，其余参数与SW1相同。分析所得的荷载-位移曲线见图6。

表6 不同含圆钢率模型参数Table 6 Model parameters with different round steel ratio

图6 不同含圆钢率荷载—位移曲线Fig.6 Load-displacement curve with different round steel ratio

由图6可知，组合剪力墙模型的刚度与强度随含圆钢率的降低而逐渐减小。本文采用位移延性系数μ来分析组合剪力墙延性的好坏，位移延性系数μ的计算公式为：

上式中Δu为构件的极限位移，Δy为构件的屈服位移。极限位移采用在试件达到峰值荷载后，随位移荷载增加而下降至峰值荷载的85%时对应点所对应的位移作为极限位移。屈服位移采用Park[12]法来确定屈服点，确定方法如图7所示。

图7 Park法Fig.7 Park method ratio

按上述方法确定屈服点与极限点，计算所得得位移延性系数见表7。

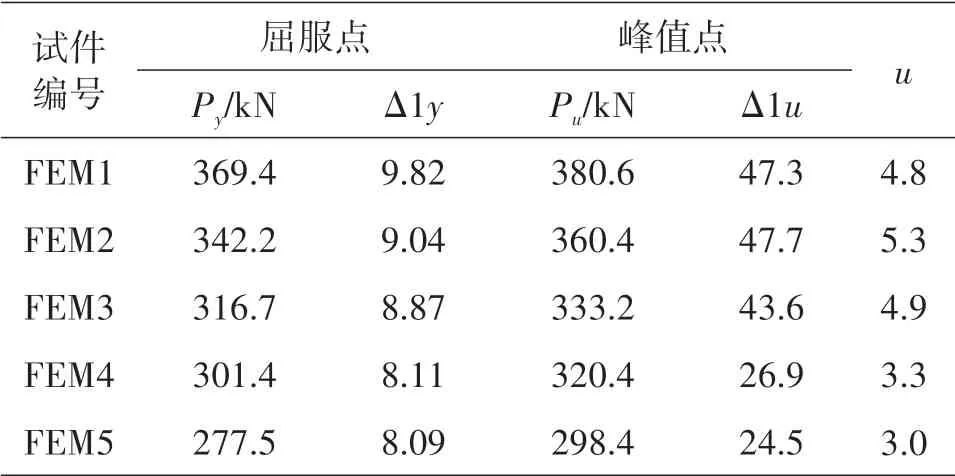
表7 延性系数Table 7 Ductility coefficient

以含圆钢率作为x轴，位移延性系数和承载力作为y轴，可以直观看出含圆钢率对组合剪力墙抗震性能的影响，结果见图8。

由图8可知，有限元模型承载力性能随含圆钢率的提高而呈线性增长。位移延性性能随含圆钢率的增加，先提高，在含圆钢率为6.5%左右时达到最高值5.3，后开始下降。

图8 延性与承载力—含圆钢率关系Fig.8 Relationship between ductility and bearing capacity-girth ratio

《建筑抗震设计规范》[13]要求现浇混凝土剪力墙在罕遇地震下的位移延性（μ＞3.0），则要求装配式内置双钢套管混凝土组合剪力墙的含圆钢率满足一定的要求，才能保证在地震下拥有良好的变形能力。组合剪力墙的截面设计可根据实际情况需求，参考图8的曲线进行优化设计。

2.4 受力机理分析

借助有限元软件分析组合剪力墙受力机理，ABAQUS可分离模型各部件，观察其应力分布情况，分析各部件间协助工作的受力机制。查看FEM1与FEM5模型加载结束后的应力分布，见图9。

图9 应力分布情况Fig.9 Stressdistribution

由图9可知，对于含圆钢率大的FEM1，受力机制主要通过加载梁传递到双钢管进行受力，在混凝土与钢管接触界面会有明显的应力集中区域。随着荷载的增加试件表现为混凝土受压区和与钢管接触区域受压脆性破坏，延性性能差。对于含圆钢率低的FEM5，由于含圆钢率低，试件主要由预制混凝土墙撑受力，在一层剪力墙底部边缘混凝土受压破坏后，组合剪力墙强度快速下降发生脆性破坏，延性性能差。只有合理的含圆钢率，才能使钢管、钢筋和混凝土更好的协同工作，使组合剪力墙发挥更好的延性性能。