基于联合对角化的MIMO雷达近场目标定位
2021-10-08周二宁
周二宁, 姜 宏, 苏 康
(1. 吉林大学, 吉林长春 130012; 2. 广东东软学院, 广东佛山 528200)
0 引言
近些年来,MIMO雷达目标定位一直是学者们研究的热点[1-3]。但对于MIMO雷达近场目标定位的研究却很少,目前大部分的近场源目标定位文献只局限于阵列信号处理,不适用于收发阵列并存的场景[4]。而近场源目标定位越来越受到重视,其中地面穿透雷达和室内定位是近场源目标定位的典型应用。
传统的目标定位方法都是基于远场假设的,尽管经典算法很多,但不能直接用于近场信号模型。而在有源阵列信号处理领域内,有关MIMO雷达近场目标定位算法的文献较少。文献[5]提出基于平行因子的双基地MIMO雷达目标定位算法,该算法信号模型中收发阵列距离较近,但阵元间隔可以拓展到λ/2;文献[6]提出一种双基地MIMO雷达近场目标四维参数估计算法,但阵元间隔局限在λ/4内;文献[7]提出的算法利用MIMO雷达接收信号的互协方差矩阵来构造二阶统计量矩阵,再通过特征值分解估计近场目标的三维参数,但此算法在加性复高斯噪声环境下角度模糊现象严重,且阵元间隔局限在λ/4内。
联合对角化算法在阵列信号处理领域和MIMO雷达远场源定位方面都有应用,而且性能较好[8-9]。本文利用联合对角化算法解决单基地MIMO雷达近场目标定位问题,并通过仿真实验证明了算法的有效性。和文献[7]所提算法相比,本文算法参数估计精度高,无角度模糊现象,而且接收阵元间隔可以拓展到λ/2。
1 MIMO雷达近场信号模型
假设这样一个场景,如图1所示:单基地雷达系统由Mt=2M+1个发射阵元和Mr=2N+1个接收阵元组成,发射阵列和接收阵列都是均匀线阵,阵元间隔分别是dt和dr,中间阵元为参考阵元;假设空间有P个目标,第l(l=1,…,L)个快拍内接收信号可以表示为:
第l个快拍(l∈[1,2,3,…,L])内接收信号可以表示为
(1)
式中,
A(θr,r)=[a1(θr1,r1),a2(θr2,r2),…,
aP(θrP,rP)]
(2)
B(θt,r)=[b1(θt1,r1),b2(θt2,r2),…,
bP(θtP,rP)]
(3)
ε(tl)=[ε1(tl),ε2(tl),…,εP(tl)]T
(4)
(5)

图1 单基地MIMO雷达信号模型
第p个目标的接收导向矢量和发射导向矢量分别为
ap(θrp,rp)=[ej(Nωrp+(-N)2φrp),…,
ej(ωrp+φrp),1,ej(-ωrp+φrp),…,
ej(-Nωrp+(N)2φrp)]T
bp(θtp,rp)=[ej(Mωtp+(-M)2φtp),…,
ej(ωtp+φtp),1,ej(-ωtp+φtp),…,
ej(-Mωtp+(M)2φtp)]T

(6)

接收信号经过发射信号sm(m=-M,…, -1,0,1,…,M)滤波后得到
Xm=A(θr,r)diag(ε(tl))dm+Nm
(7)
式中,dm=[ej(-mωt1+(-m)2φt1),ej(-mωt2+(-m)2φt2),…, ej(-mωtP+(-m)2φtP)]T。
将式(7)矢量化得到

[a1⊗ej(-mωt1+(-m)2φt1),…,
(8)
式中,“⊗”表示求Kronecker积。在L个快拍后,式(8)变成
Ym=Amε+Zm
(9)

2 算法描述
所提出的算法主要包括3个部分:首先,根据接收信号构造相关矩阵;其次,构造选择矩阵,利用相关矩阵和选择矩阵,通过联合对角化算法得到自动配对的发射角和距离估计值;最后,通过谱峰搜索得到接收角估计值。
求Ym和Y0之间的互协方差矩阵,即

(10)
式中,Rε=E⎣εεH」。取m=-1,0,1,则
(11)
(12)
(13)
利用互协方差矩阵R-1,0,R0,0和R1,0构造矩阵R:
(14)

R=USVH
(15)
式中,S为R的奇异值矩阵,U和V为相应的奇异向量矩阵,则信号子空间Up=UsSs包含方向信息,其中Ss是P个最大奇异值组成的对角阵,Us是相应的奇异向量矩阵。
定义3个矩阵:
则发射角θt和距离r的选择矩阵可以表示成
K1=J1⊗I
(16)
K2=J2⊗I
(17)
K3=J3⊗I
(18)
式中:I为Mr×Mr的单位阵;K1,K2,K3分别用来选取Up中和R-1,0,R0,0,R1,0对应的子块。
根据联合对角化方法[8],定义两个矩阵:
G1=(K1Up)-1K2Up=TD1T-1
(19)
G2=(K3Up)-1K2Up=TD2T-1
(20)
式中,
D1=diag[ej(-ωt1-φt1),…,ej(-ωtP-φtP)]
(21)
D2=diag[ej(ωt1-φt1),…,ej(ωtP-φtP)]
(22)
则对角矩阵D1和D2中包含发射角和距离信息,且G1和G2具有相同的特征向量矩阵。分别对G1和R0,0进行特征值分解:
(23)
(24)

(25)

D=diag[ej(2ωt1),…,ej(2ωtP)]
(26)
令ρtp=ej(2ωtp),p=1,2,…,P为D的对角线元素,则第p个目标的发射角可以用下式计算:
(27)
式中“∠”表示求相位角。

(28)

(29)

(30)
3 算法仿真
仿真实验一: 假设两个目标的信噪比为SNR=10 dB,进行20次重复实验,得到两个近场目标的参数估计值和配对结果,实验结果如图2所示。由图2可以看出,该算法可以实现单基地MIMO雷达近场目标三维参数联合估计,三维参数可以实现自动配对,而且精度较高。
仿真实验二: 假设两个目标的信噪比(SNR)从0 dB到30 dB变化,进行100次重复实验,得到3个参数估计值的均方根误差(RMSE)随信噪比的变化曲线,实验结果如图3~图5所示。其中RMSE的定义如下:
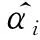

图2 两个近场目标的参数估计和配对结果

图3 接收角估计RMAE

图4 发射角估计RMSE

图5 距离估计RMSE
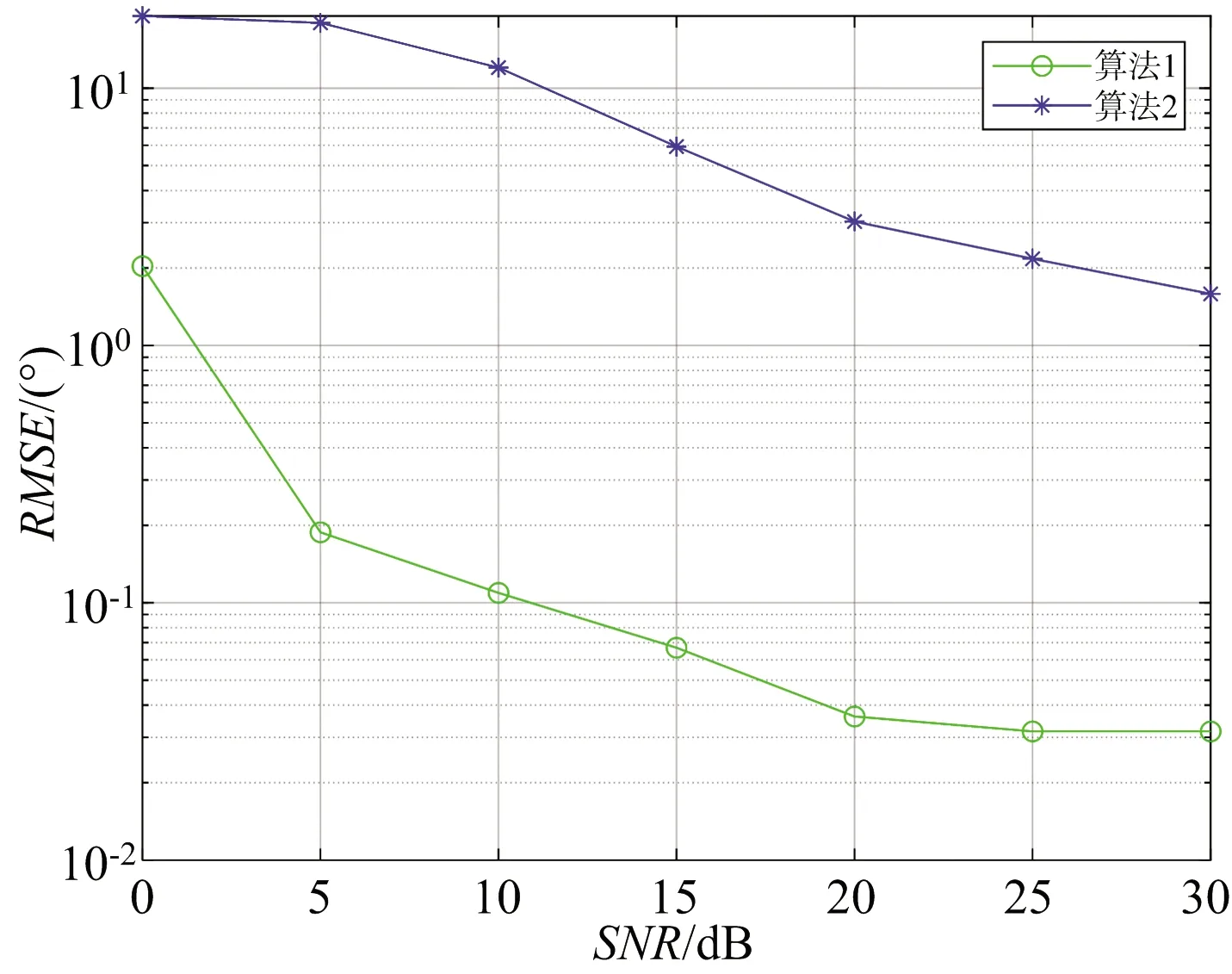
(a) 接收角估计值RMSE对比图

(b) 发射角估计值RMSE对比图图6 角度估计性能对比图

图7 距离估计性能对比图
仿真实验三:为了进一步验证算法的有效性,和已有算法进行如下对比实验。噪声为复高斯白噪声,信噪比(SNR)从0 dB到30 dB变化,进行100次重复实验,对比本文所提算法(算法1)和文献[7]所提算法(算法2)的参数估计值的RMSE随信噪比的变化曲线,结果如图6~图7所示。从图中可以看出:在高斯复噪声环境下,本文所提算法的精度明显高于文献[7]所提算法,文献[7]所提算法具有角度模糊现象,导致参数估计值的RMSE偏大,而且RMSE曲线不平滑。
4 结束语
本文提出了一种基于联合对角化的单基地MIMO雷达近场定位算法。该算法利用收发呈十字形的阵列模型,基于3个参数联合估计有效地解决了单基地MIMO雷达近场目标定位问题,参数可以自动配对,并具有较高的精度。此外,该算法对雷达系统的复杂度要求不高,只需3个发射阵列就可估计出近场目标的三维参数。另外,和文献[7]算法相比,所提算法在接收阵元间距为λ/2时依然有效,适用于任何高斯噪声环境。
