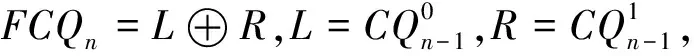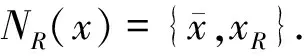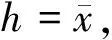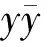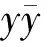折叠交叉立方体的限制连通度

2021-10-08阿斯牙米吉提

北华大学学报（自然科学版） 2021年5期

阿斯牙·米吉提

(喀什大学数学与统计学院，新疆喀什 844000)

0 引言

众所周知，互联网络在并行计算/通信系统中起着重要的作用.在多处理器系统中，处理器通常根据由图G=(V，E)表示的某种互连网络连接，其中V中的每个顶点对应于处理器，E中的每条边对应于通信链路.图的性质决定了系统的工作效率.可靠性是选择或设计互连网络时必须考虑的重要度量之一，评价互连网络可靠性的两个重要参数是点连通度和边连通度.连通图G的点连通度κ(G)(边连通度λ(G))是顶点子集(边子集)的最小基数，将其删除后图G不连通.然而，这两个参数都有一个明显的不足，即它们默认地假定一个顶点附近的所有顶点(或与一个顶点相关联的所有边)都可能同时失效，这在实际的多处理器系统中几乎是不可能的.后来人们发现仅有点连通度和边连通度不能够准确反映处理器和通讯信道受损时系统的损坏程度.为此，Harary于1983年首先提出条件连通度的概念[1]，Esfahanian和Hakimi于1988年更进一步提出了限制连通度的概念[2].本文中，我们将关注折叠交叉立方体的2-限制点(边)连通度.

n-维交叉立方体CQn[3-4]和n-维折叠超立方体FQn[5]被认为是计算机系统中最通用、最高效的两种互联网络.2002年，文献[7]中提出了一种基于n-维交叉立方体和折叠超立方体的互联网络——折叠交叉立方体(FCQn).FCQn是一种高性能、低成本的构架，具有短直径、短平均节点间距离和非常低的消息流量密度等吸引人的特性，文献[6-8]分别研究了FCQn的不同的性质.设子集F⊆V(G)(F⊆E(G))(如果存在)称为h-限制点割(h-限制边割)，如果G-F不连通，并且G-F中的每个连通分支至少有h+1个顶点，其中最小的h-限制点割(h-限制边割)的基数称为图G的h-限制连通度(h-限制边连通度)，记为κh(G)(λh(G)).近几年，对限制连通性的研究有着极为丰富的研究内容，并得到了一些漂亮的结果[9-11].本文中，我们确定了n-维折叠交叉立方体FCQn的2-限制(边)连通度，证明了κ2(FCQn)=3n-1(n≥8)以及λ2(FCQn)=3n-2(n≥7).

1 定义及引理

定义1设x和y是两个2长的二元字符串，如果(x，y)∈{(00，01)，(10，11)，(01，11)，(11，01)}，则称x和y为相关对，并记为x～y.

n-维超立方体Qn的顶点集是由2n个n长的二元字符串组成的，其中任意两个顶点相邻当且仅当它们的汉明距离等于1.n-维交叉立方体CQn(n≥2)是一无向图，它的顶点集和Qn的顶点集一样，两个顶点x=xnxn-1…x2x1和y=ynyn-1…y2y1相邻当且仅当存在j(1≤j≤n)使：

(a)xn…xj+1=yn…yj+1；

(b)xj≠yj；

(c)xj-1=yj-1，如果j是偶数；

(d)x2ix2i-1～y2iy2i-1，i=1，2，…，「(1/2)j⎤-1.

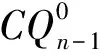
图1 3-维交叉立方体CQ3和FCQ3Fig.1 3 dimensional crossed cube CQ3 and FCQ3

引理1[12]CQn是n-正则的，有2n个顶点，(n+1)2n-1条边.

引理2[13]κ(CQn)=λ(CQn)=n.

引理3[14]κ1(CQn)=λ1(CQn)=2n-2.

引理4[8]κ(FCQn)=n+1.

引理5[15]对n≥2及任意u∈V(CQn)，CQn-NCQn[u]是连通的.

引理6[15]FCQn(n≥4)不含三角形.

引理7[12]对互异的两点u，v∈V(FCQn)，|NFCQn(u)∩NFCQn(v)|≤2(n≥4).

2 主要结果

定理1对于n≥7，κ2(FCQn)≤3n-2.

证明：由引理7可知，当n≥4时，可以在FCQn中选取两个不相邻的点u、w，使得|N(u)∩N(w)|=2.取u、w的一个公共邻点v，且令X={u，v，w}，S=NFCQn-X(X)，则由X的选法，得|S|=|NFCQn-X(X)|=3n-2，且S是一点割，其中FCQn-S的一个分支X具有3个顶点，令Y=FCQn-S-X，由于|S∪X|=3n+1

κ2(FCQn)≤|S|=3n-2.

证毕.

定理2对于n≥8，κ2(FCQn)=3n-2.

情形1.R-KR连通.

情形2.R-KR不连通.

令K′R=KR∪{h}，K′L=KL，则|K′R|≤⎣(3n-3)/2」+1<κ1(R)=2n-4(n≥7)，R-KR-h不含孤立点，说明R-KR-h连通.回到情形1，即L-K′L中任意点都与R-K′R连接.根据假设知，点h在FCQn-K中存在邻点，而此邻点与R-KR-h连接，从而h可通过某条路与R-KR-h连接.因此FCQn-K连通.综合情形1与2，得

κ2(FCQn)≥3n-2.

证毕.

定理3对n≥4，λ2(FCQn)≤3n-1.

若x∈X，则结论成立.若x∈NFCQn-X(X)，则因dFCQn(x)=n+1，再由引理7可知，|N(x)∩X|≤ 2，因此dFCQn-E(X)(x)≥n+1-2=n-1>2(n≥4)，结论成立；若x∈VFCQnN[X]，则此时dFCQn-E(X)(x)=dFCQn(x)=n+1>2，结论成立，即E(X)是FCQn的一个2-限制边割，从而λ2(FCQn)≤|E(X)|≤3n-1(n≥4).证毕.

定理4对n≥7，λ2(FCQn)=3n-1.

证明：由定理3可知，只需证λ2(FCQn)≥3n-1(n≥7).令K是FCQn的一个边集，|K|≤3n-2，且FCQn-K不含任何孤立点和孤立边.为了证明λ2(FCQn)≥3n-1，只需证FCQn-K是连通的.令FCQn=L⊕R，M是L与R之间补边与交叉边的全体.再令K=KL∪KM∪KR，其中KL=K∩L，KM=K∩M，KR=K∩R.因为R-KR要么连通，要么不连通，故分两种情形讨论.

情形1R-KR连通.

当(NL(x){y})∩(NL(z){y})=∅时，上述路共有3n-7条，且任意两条路无重边.

当(NL(x){y})∩(NL(z){y})≠∅时，根据引理7，存在唯一的一个顶点a∈(NL(x){y})∩(NL(z){y})，另取R中的点aR与a相连，此时pi∪pj∪p′∪{aaR}共有3n-7条路，且任意两条路无重边.由|KL|+|KM|+|KR|≤3n-2，以及|KM|≥6知，|KL|+|KM|-6≤3n-8<3n-7，故上述两种情况下3n-7条路中必有某条路与KL∪KM无重边，x通过此条路与R-KR连接.

情形2R-KR不连通.

因为|KL|+|KM|+|KR|≤3n-2，所以|KL|+|KR|≤3n-2-|KM|<3n-2，不妨设|KR|≤|KL|，则|KR|≤ ⎣(3n-2)/2<λ1(R)=2n-4(n≥7).由引理3可得，R-KR含孤立点h，所以R中与h相邻的边集ER(h)⊆KR.又因dR(h)=n-1，且|KR|<2n-4，则有|KR|-|ER(h)|≤n-4.对任意t∈V(R-ER(h)-h)，dR(t)≥n-2>n-4，从而R-KR-h不含孤立点，下证R-KR-h必连通.

用反证法.若它不连通，则连接点h与h在R中的一个邻点hN，可以得到一新图R-KR∪{hhN}，且此图仍不连通，此图是由R删掉2n-6条边得到，且无孤立点.但另一方面，由引理3知，R-KR∪{hhN}连通，矛盾.因此R-KR-h必连通，且此时|KR|≥n-1，从而|KL|+|KM|=|K|-|KR|≤2n-1.现只需证任意x∈L-KL，x与R-KR-h连接，而h与L-KL中的某个点相邻，h通过此点连接到R-KR-h.此情形下有三种情形：

情形2.1|KL|≤2n-5.