基于深度Q-学习和粒子群优化的僵尸检测算法*
2021-10-08任勇军
顾 伟 任勇军
(南京信息工程大学计算机与软件学院 南京 210044)
1 引言
活跃于社交网络平台的社交机器人(Social Bot,SB)实质是一个自动计算机程序[1]。这些SBs可分为僵尸SB、干扰SB和诚意SB。这些恶意SBs也称为僵尸攻击,它们分布于垃圾邮件、钓鱼网。干扰SBs用于操控在线评论和评分,进而干扰用户的行为[2]。而诚意SBs正常地发布产品消息、新闻资信。
现有多种检测在线社交网络上的僵尸[3~4]算法。然而,僵尸会动态地改变其行为,进而避免检测。目前主要有基于机器学习、基于众包(Crowdsourcing)和基于社会图谱的僵尸检测算法。
基于机器学习的检测算法通过考虑多项特征数据,从SBs中分离合法的SB。文献[5]提出基于随机森林分类器的BotorNot检测算法。文献[6]采用了基于深度Q-学习的僵尸检测算法。
基于众包的检测算法是利用专家库构建评判标准,进而对SB进行分类。例如,文献[7]针对2000个账户数据,并基于10个专家评判,建立分类标准。
基于社会图谱的检测算法是采用社会网络图谱对SB进行分类。目前,有基于用户间的社会信任关系和基于中心测量和图拓扑两种类型。文献[8]采用基于Sybil随机-漫步的方法检测Sybil用户,其中不信任用户的分数最低,而合法用户的分数最高。文献[9]采用了基于中心测量的算法,并提出了基于神经网络、随机森林和决策树分类器。
在传统的Q-学习算法中,所有学习动作均需计算其Q值。因此,Q-学习算法的收敛速度很慢,增加了存储所有动作的Q-值的空间。
为此,提出基于深度Q-学习和粒子群优化的僵尸检测(Deep Q-Learning and Particle Swarm Optimization-based Bot Detection,DQL-PSO)算法。利用粒子群算法优化Q-学习,进而获取最优的学习动作序列。仿真结果表明,提出的DQL-PSO算法提高了检测算法的收敛速度,并提高了检测僵尸的准确性。
2 网络模型
引用如图1所示的网络架构。每个粒子代表一个状态,并且每个粒子有n个序列的学习动作,且每个序列对应一个Q值。在随机环境中,先计算每个粒子的适度值。再依据适度值,更新学习动作的局部和全局最优序列。因此,通过载入新的粒子,更新迭代,进而优化性能。

图1 网络框架
3 DQL-PSO算法
3.1 基于PSO的Q函数的更新
DQL-PSO算法利用粒子群优化(Particle Swarm Optimization,PSO)对Q函数进行更新。将僵尸的检测问题转化为优化问题,提高检测性能。
令S={s1,s2,…}和LA={α1,α2,…}分别表示状态集和学习动作集。每个用户行为关联了状态和学习动作,再依据用户行为,对用户进行奖励。
引用文献[12]的定义,令st和令αt分别表示当前的状态和动作。令表示下一个状态。在时间t获取了奖励rt。据此,定义状态转换函数:
通过优化学习动作序列,进而最大化累加奖励R。用fst(A)表示优化后的动作序列的适度函数:fst(A)=R(st,A)。而。
当在时刻t执行动作αt,位于状态st的学习代理就得到奖励rt。DQL-PSO算法的根本目的就是最大化累加奖励,决策最优的动作集序列。因此,对适度函数fst(A)进行更新:

式中:T表示在每个学习时期内总的学习动作数。rt表示第t个动作的当前奖励。而γ表示折扣因子,且γ∈(0,1)。
针对SB检测问题,用动作集序列A={αt,αt+1,…}表示粒子位置;用状态转换率表示粒子速度。并且通过比较适度函数决定每个学习代理的局部最优解和所有学习代理的全局最优解。

式中:ω、c1和c2分别代表权重系统。而r1、r2为随机数,且在0~1之间。Qi(st,αt)表示第i个粒子在状态st所选择的动作αt所形成的Q-值。而表示由第i个粒子决策的局部最优Q值。Gbest(st,αt)表示由所有粒子决策的全局最优Q值。
3.2 检测步骤
DQL-PSO算法的检测步骤如算法1所示。每个用户的执行步骤:
1)依据式(2)计算累加奖励R;
2)依据最优的学习动作集A,计算局部和全局最优Q值;
3)再依据式(3)和式(4)更新速度和Q值。
重复上述过程,直到达到迭代次数。
Algorithm 1
Parameters:
R:Cumulative reward for Q-valueQ(s,α)

具体而言,首先对Qi(s,α)以及Vi(st,αt)进行初始化。并以状态s1进行学习。然后,代理在时刻t执行动作αt获取当前奖励rt以及下一个相应的状态,并缓存经历值。
再依据式(2)计算奖励值Ri,再更新粒子的局部最优位置。若Ri小于或者=-1,就将当前位置作为局部最优位置,并将当前Q值作为局部最优Q值,如式(5)所示:

将所有粒子中具有最高Q值的位置作为全局最优解,如式(6)所示:

图2给了DQL-PSO算法的执行流程。先对参数进行初始,再评估每个粒子的适度值。然后,再选择局部最优和全局最优值。随后,依据局部和全局最优值更新每个粒子的位置和速度。并进行迭代,若达到迭代次数,就停止迭代。

图2 DQL-PSO算法的执行流程
4 性能仿真
为了更好地分析DQL-PSO算法的性能,选择文献[10]的用户群数据库(User Popularity Dataset,UPD)作为实验数据。其中用户数为453853,合法用户数为476,僵尸个数为320。最大的迭代次数为30。其余的仿真参数如表1所示。

表1 仿真参数
选择文献[11]提出的同步策略的PSO算法(Heterogeneous Strategy PSO,HS-PSO)和文献[6]提出的自适应深度Q-学习的(Adaptive Deep Q-learning,ADQL)算法作为参照。主要比较它们的达到最优状态的动作序列数(以下简称为最优-动作序列数)、准确率Pprecision和重放率PRecall。
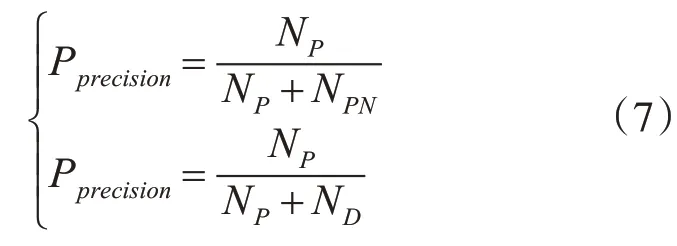
式中:NP表示正确地将僵尸评判为僵尸的数量。而ND表示错误地将SB评判为合法的SB的数量。而NPN表示将合法用户评判为僵尸的数量。
4.1 最优-动作序列数
首先,分析在不同迭代次数下的DQL-PSO算法的最优-动作序列数,如图3所示。图3记录了30次的迭代次数。

图3 最优-动作序列数
从图3可知,相比于HS-PSO算法,提出的DQL-PSO算法在同等的迭代次数环境下,所需的学习动作数少,降低了最优-动作序列数。例如,迭代次数为25次时,HS-PSO算法的最优-动作序列数达到约28.5,而DQL-PSO算法的最优-动作序列数低至22。
4.2 准确率
图4显示了在不同学习时期下ADQL和DQL-PSO算法的准确率。图4反映了两项信息:1)收敛性;2)准确值。从收敛角度,DQL-PSO算法的性能优于ADQL算法。DQL-PSO算法未到300个学习时期收敛,并收敛于95%。而ADQL算法约在350个学习时期收敛。从准确值角度,DQL-PSO算法的准确值也优于ADQL算法。DQL-PSO算法的准确值收敛于95%,而ADQL算法的准确值收敛于约92%。
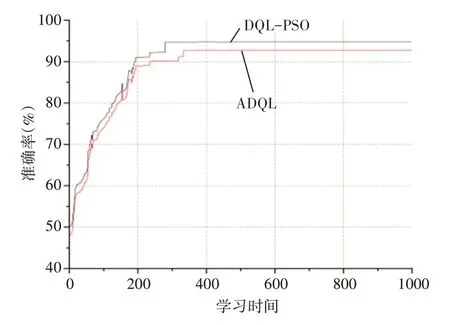
图4 准确率
4.3 重回率
最后,分析DQL-PSO算法和ADQL算法的重回率,如图5所示。相比于ADQL算法,提出的DQL-PSO算法的重回率得到提升。例如,ADQL算法的合法用户的重回率约93%,而DQL-PSO算法的重回率约95%。

图5 重回率
5 结语
在深度Q-学习算法中,学习代理依据更新Q-值自动学习。此外,通过有效选择更新策略可以快速地收敛。本文采用DQL-PSO算法检测僵尸。利用粒子群优化算法更新Q函数。并利用局部最优Q值和全局最优Q值更新Q值。
利用UPD数据库进行分析,并与HS-PSO和ADQL算法进行比较,仿真结果表明,提出的DQL-PSO算法能达到95%的检测准确率和93%的重回率。相比于HS-PSO算法,DQL-PSO算法提升了收敛速度。
