Ф-OTDR非平稳信号的连续时频域分析

徐涛 李黎

摘 要：多数自然振动为平稳信号，且受光纤分布式振动传感系统的干涉光信号调制。作为事件识别关键参量之一的幅值信息无法采用传统信号分析方法准确获得。本文基于分数阶傅里叶变换在统一的幅、时、频域内更准确地提取Phase-sensitive optical time domain reflectometry（Ф-OTDR）信号的幅值信息。在分析Ф-OTDR非平稳信号形成原因的基础上，进一步讨论分数阶傅里叶变换的适用条件，最后在实际地下电气管廊第三方破坏中检测分数阶傅里叶变换提取Ф-OTDR信号的幅值信息的有效性。分数阶傅里叶变换在连续的幅、时、频域分析中，更准确地提取非平稳振动信号的幅值信息，有助于Ф-OTDR事件探测与类型分析。

关键词：Ф-OTDR;分数阶傅里叶变换;非平稳信号;振动事件识别

DOI：10.15938/j.jhust.2021.04.020

中图分类号：O439;TP212

文献标志码：A

文章编号：1007-2683（2021）04-0146-07

Abstract：Most of the natural vibration signals are stationary and modulated by the interference light signal of the distributed optical fiber vibration sensing system. As one of the key parameters of event recognition， amplitude information cannot be accurately obtained by traditional signal analysis methods. This paper used the fractional Fourier transform（FRFT） method to analyze the nonstationary vibration signal of Ф-OTDR. In the unified amplitude， time and frequency domain， the amplitude of nonstationary signal can be extracted more accurately than the conventional method. Based on analyzing the causes of the non-stationary signal of Ф-OTDR， the applicable conditions of FRFT are further discussed. The effectiveness of extracting the amplitude of Ф-OTDR signal by FRFT is validated by the actual third-party damage of urban electric pipe gallery. In the continuous amplitude， time and frequency domain analysis， the fractional Fourier transform can extract the amplitude information of non-stationary vibration signal more accurately， which is helpful to improve the accuracy Ф-OTDR event detection and type analysis.

Keywords：Ф-OTDR; fractional Fourier transform; nonstationary signal; vibration event identification

0 引 言

相位敏感光時域反射（Φ-OTDR）光纤振动传感系统，具有高灵敏度、无源供电、良好隐蔽性、抗电磁干扰、可多点同时定位等优点，广泛应用于周界安防、油气电管廊、通信等重要民生工程。振动信号的处理技术并提取特征的优劣决定了系统振动事件定位与特征识别。因此对其研究成为研究热点。近年来国内外大量报道Ф-OTDR的信号分析。Vries[1]应用频域特征与神经网络相结合的方法识别不同入侵事件。罗光明等[2]利用不同尺度下方差分布的特征区分入侵行为。冯欣等[3]提出小波分析与信熵结合的方法区分噪声与信号。Tan等[4]利用信号强度特征识别车辆经过、人工挖掘、以及挖掘机挖掘三种模式。Zhu等[5]应用短时过电平率有效区分埋墙环境下的攀爬、踢、浇水三类行为模式。蒋立辉等[6]基于总体平均经验模态分解与双重支持向量法识别攀爬、敲击、汽车、风四类入侵行为。郑印等[7]采用小波分析与自适应均值去阈值的方法识别不同频率振动事件。吴俊等[8]基于多尺度一维卷积神经网络的光纤振动事件识别破坏、敲击、干扰信号。盛智勇等[9]基于随机配置网络的光纤入侵信号识别算法降低光了约4%的测试误差，有效提升了系统的普适性。Z Qin等[10]提出了一种基于经验模态分解（EMD）的新型去噪方法，以提高相敏光时域反射仪（-OTDR）系统中振动传感的信噪比。Marcel[11]利用传统的图像和视频处理方法滤除分布式光纤传感信号中的相似性和冗余性信息，显着提高信噪比达100倍。 Tabi等[12]提出了一种基于功率谱估计的二级振动模式识别方案，实现实时有效地识别沿传感电缆的任何入侵事件，入侵检测率大于95%。Z Wang等[13]提出了一种基于经验模态分解（EMD）和极端梯度增强（XGBoost）的模式识别新方法，实时识别出五种干扰事件，包括浇水，爆震，攀爬，挤压和假干扰事件，其有效性优于其他常用方法。Yi Shi等[14]提出了一种基于深度学习的事件识别方法。直接使用来自Φ-OTDR的时空数据矩阵作为卷积神经网络（CNN）的输入。使用简单的带通滤波和灰度转换实现实时处理，还构建了一种体积小，训练速度快，分类精度高的网络结构 。Bernard[15]提出了一种识别光纤振动信号的时频特性方法， 基于希尔伯特（Hilbert）变换和所描述的时频熵和重心频率的经验模式分解（EMD），形成一个特征向量，并对其执行多种类型的概率神经网络（PNN），以确定是否发生入侵事件。对此问题仍在持续研究中，但迄今为止，仍没有有效的信号处理方法。虽然各类方法与判断指标层出不穷，但振动能量仍是Φ-OTDR的信号特征分析的首要判断指标。前人大多采用单一的幅值域、或时域、或频域分析方法分析振动能量，存在局限性，如小波分析方法实质是一种窗口可调傅里叶变换，没有摆脱傅里叶变换束缚。傅里叶变换是分析和处理平稳信号的一种标准和有力的工具，它是一种全局变换方法，得到的是信号的整体频谱，但在实际应用中，信号大多是非平稳的，其统计量（如均值 、相关函数、功率谱等）是时变的，时域和频域绝对分离，即在频域不包含任何时域信息，在时域中同样找不到任何频域信息。不可能同时在时域和频域都具有良好的定位的能力。无法得知某一频率产生时间，且采用传统的傅里叶变换无法表述信号频谱随时间变化的情况。传统傅里叶变换无法将某一振动事件引起的信号各频率的能量聚集在一起。傅里叶变换以三角正弦或余弦函数为基，无法分析非平稳时变信号。因此于1980年提出分数阶傅里叶变换，其本质上是一种统一的时频变换，同时反映了信号在时域和频域上的信息。与传统的傅里叶变换相比，它更适用于处理非平稳信号，尤其是线性调频（啁啾）信号。其在音频讯号、雷达与声呐系统、波物理学、机械与震动、生物与医学等领域有广泛应用[16-21]。

本文首次采用分数阶傅里叶变换对Φ-OTDR的振动信号进行处理，该方法可综合幅、时、频域分析方法，在统一的时频连续变换中准确提取非平稳信号特征频率的能量幅值。首先简述Ф-OTDR的原理并阐述其非平稳啁啾信号的形成原因;其次解释采用分数阶傅里叶变换分析Ф-OTDR信号的必要性以及适用条件与方法;最后分析真实环境中Ф-OTDR事件的幅值响应情况，验证分数阶傅里叶变换的有效性。该方法可有效地提取非平稳信号的幅值信息，有助于Ф-OTDR事件分析与识别。

1 Ф-OTDR非平稳信号分析

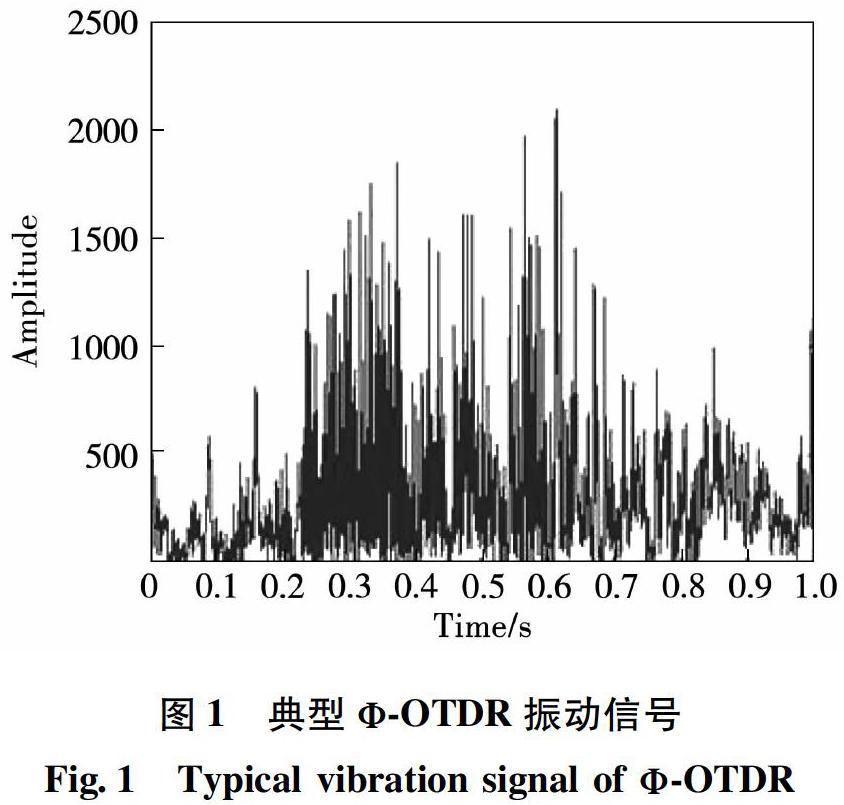
Ф-OTDR传感原理本质上是脉冲光内的干涉统计结果，由于系统元器件噪声、干涉光学信号的非线性、振动激励源的非平稳性、传感光缆系统的材料非线性，以及各种随机噪声，导致Φ-OTDR监测所采集的各种振动信息的频率特性不同，与此频率特性相对应的能量信息也不同，因此对特征频率的能量信息分析是事件类型判断最直接有效的方法。图1为Ф-OTDR的典型振动信号，明显是一个非平稳信号，其周期由密集逐渐变稀疏。典型振动信号的近似系数由低频部分组成，涵盖了光脉冲信号的大部分轮廓信息，而细节系数由信号的高频部分组成，往往包括扰动引起的突变和大部分噪声。Ф-OTDR振动信号频率成分并不单一，且随时间变化，即非平衡振动信号。该信号的传统傅里叶变换频谱分布宽且幅值变小，可能被噪声淹没。

1.1 非平稳振动信号的分數阶傅里叶变换分析

信号的分数阶变换可以认为是在时频平面中，坐标轴绕原点逆时针旋转任意角度的表示方法。信号f（t）在α角度下的分数阶傅里叶变换的定义为

式中：j为复数符号;p为傅里叶阶数。式（3）定义表明分数阶傅里叶变换是关于时频坐标旋转角α和u的函数。令阶次p=2α/π，当p=1时，此时旋转角

度为π/2，分数阶傅里叶变 f-1（u）就是f（t）的传统的傅里叶变换;当p=-1时，f-1（u）就是f（t）的传统的傅里叶逆变换;同时，FRFT满足阶数可加性（指数可加性，或旋转可加性）。所以可以认为分数阶傅里叶变换是一种广义的傅里叶变换。

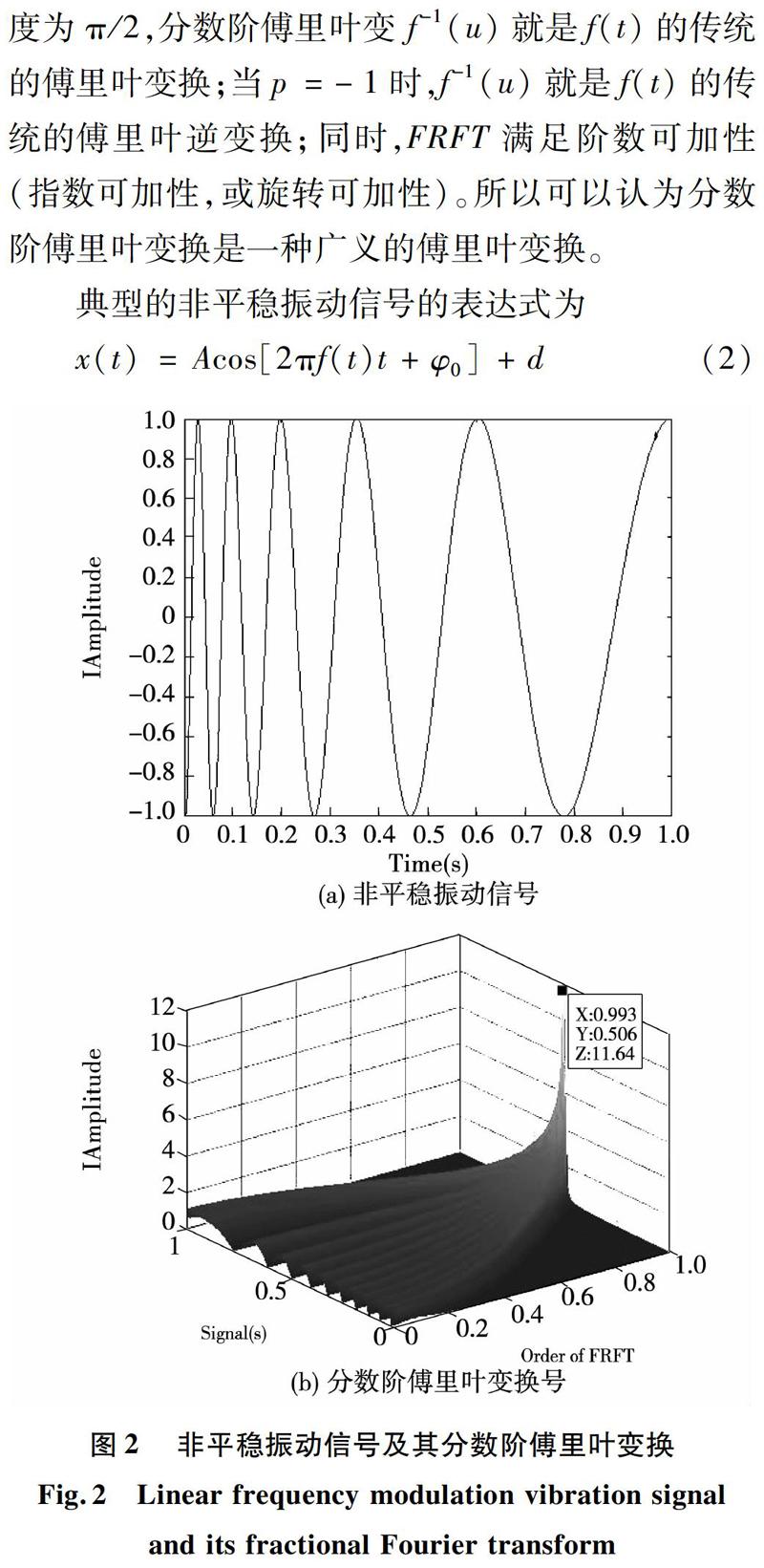
典型的非平稳振动信号的表达式为

其中：A为信号幅值;f为频率;t为时间;φ0为初始相位;d为直流分量。如图2（a），假设非平稳振动信号的频谱为0至50Hz，分数阶傅里叶变换如图2（b），以0.01步长逐渐从0阶（对应时域信号）过渡至1阶（对应普通傅里叶变换，此时幅值最大值为6.285）。由于传统傅里叶变换能量分散在各频率，导致最大幅值偏低。为确定非平稳振动信号的最大幅值，采用二维峰值搜索法，即以阶次p和分数阶傅里叶频域坐标u为二维平面，计算在每一阶次p处信号的分数阶傅里叶变换。为简化计算，可将二维峰值搜索分两部分，即粗与细搜索。在较大阶次范围中，使用阶次步长较大的粗搜索确定峰值大致位置。在该位置附近设置阶次范围，使用较小的阶次步长进行细搜索，以确定峰值的精确位置。在指定阶次的分数阶傅里叶变换二维图中，最大值是非平稳振动信号在二维平面上的能量聚集，相应的阶次就是最佳阶次。如图2（b）所示，非平稳振动信号在0.993阶时的最大幅值为11.64，该值远大于传统傅里叶变换所得幅值。窗口可调傅里叶变换与分数阶傅里叶变换，其本质上都是傅里叶变换。传统傅里叶变换仅能观察频域的能量幅值，特别是非平稳振动信号，其频谱能量分散于各个频率上;而分数阶傅里叶变换具有能量聚集的特性，在其连续地从0阶变换至1阶（即从时域连续变换到频域）过程中，在某一分数阶的时频谱里，可将不同频率分量上的能量汇聚在一起。

1.2 分数阶傅里叶变换的Ф-OTDR适用范围

为分析分数阶傅里叶变换的适用条件，本小节讨论啁啾信号各参量变化对分数阶傅里叶变换的影响。图3（a）为线性调频信号的频率f从0变化至100，线性啁啾信号的幅值单调递减，在频率0～10Hz时能量极大值下降很快，而在机械震动的一般频率范围内（10～80Hz）能量极大值缓慢下降。虽然振动信号有许多倍频量，但其高频成分对信号幅度贡献很小。因此在一般机械振动频率区间内，调频导致的能量极大值变化不大。所以分数阶傅里叶变换分析Ф-OTDR测得的机械振动信号幅值具有一般意义。图3（b）线性啁啾信号（幅度为A=1）的直流分量d从-1变至1， 可见-0.5～0.5的幅度区间内能量极大值基本处于稳定值，因此，被分析的啁啾信号必须去直流处理，即Ф-OTDR的迹线应做相邻相减。图3（c）线性啁啾信号的振动幅值A从-10变至10，可见啁啾信号的幅度越大，则能量极大值越大。由于Ф-OTDR信号的幅度受限于激光脉冲，对应的振动光信号幅值随振动能量增大，并趋于某一稳定值;而其频率则受光干涉原理的调制，振动信号越强烈，等效的信号频率越高，能量极大值略有降低。综合上述分析，分数阶傅里叶变换分析Ф-OTDR振动信号前，需对其去直流处理，且调频范围在10～80Hz间的能量具有可比性。因此，在实际信号处理步骤，首先应滤除信号中的直流信号;其次要对信号作归一化处理;最后采用输出分数阶傅里叶变换信号的合适频宽（如半高宽）进行滤波处理。

2 Ф-OTDR振动信号的验证分析

2.1 实验方案

为验证分数阶傅里叶变换分析Ф-OTDR信号的能量的有效性，搭建Ф-OTDR系统，脉冲光入射光强为200mW，扫描频率为5000Hz，待测光缆长度为5km，末端100m埋置于距地面0.5m深的泥土地中，传感光缆距挖掘点5m。监测挖掘机破挖掘信号，如图4所示。测得信号后，根据分数阶傅里叶变换的适用条件，相邻信号相减以去直流信号。所得振动信号如图5（a）所示，在1s内的破碎与挖掘行为的时域信号幅度不超过400。由于某一振动事件的能量分散在各频率分量上，其时域信号未能真实体现行为的能量幅值。利用分数阶傅里叶变换可聚集非平稳振动信号各频率分量的能量。由于不同的分数域内能量聚集性不同，故以上小节的峰值搜索方法查找。在时频域内对微弱的地震波信号进行峰值搜索。如图5（b），随阶数增加，时域信号的振动能量逐渐聚集，在0.9863阶时幅值最大611.1。这一能量对应于Ф-OTDR探测的某一事件。相比于时域信号幅值，分数阶傅里叶变换后聚集的能量峰值增大了52%以上。在多次检测中仍有相似结果。分数阶傅里叶变换的正交基为一系列的线性调频函数，故更适用于分析非平稳信号，特别是线性调频信号。分数阶傅里叶变换克服了传统信号分析方法无法兼顾时、频域与幅度的问题，有效提高事件振动能量判断的准确性。

此外，采用分数阶傅里叶变换滤除噪声，可得Ф-OTDR非稳振动信号。对于实际监测的挖掘机破挖掘行为的三次冲击信号进行滤波，可得如图6时域信号。滤波前的三次挖掘行为几乎无区分，滤波后明显可见三次独立的挖掘行为。分数阶傅里叶变换的滤波方法与传统傅里叶滤波相同。当搜索到挖掘行为的最大幅值与变换阶数后，将峰值两边的时频分量设为零，再做分数阶傅里叶反变换，将与非平稳信号无关的分量去除，可得滤波后的信号。

综上分析，虽然非平稳振动信号可能是非线性调频及多个线性调频信号复合，但相比传统傅里叶变换与小波变换，它能够更好地反映非平稳信号的幅值信息。振动能量幅值作为识别振动事件的判断标准之一，对于Ф-OTDR振动事件分析与识别具有重要意义。此外，分数傅里叶变换滤波也能更好地滤除背景噪声，保留非平衡振动信号。

由于实际环境工程限制，本文采集样本为模拟实验样本，下一步工作可考虑实际工程事件监测采样，如汽车正常行驶事件、行人入侵脚步、风镐振动、电锯切割等。由于不同的振动系统具有不同的固有频率，振动源也互不相同。在采用分数阶傅里叶变换取得振动事件幅值信息的基础上，结合其他数据分析方法探讨更准确提取能量的方法，进一步结大数据分析、人工智能等方法识别振动事件类型。

3 结 论

本文应用分数阶傅里叶变换对Ф-OTDR非平稳振动信号进行分析。在阐述Ф-OTDR系统原理的基础上，分析了其信号非平稳的原因。采用分数阶傅里叶变换对非平稳信号的处理效果，并研究其适用范围。在实际环境中检验基于分数阶傅里叶变换提取的Ф-OTDR振动特征频率的能量幅值，明显可见非平稳信号中的调频部分能量被压缩并与噪声分离，证明了分数阶傅里叶变换更准确提取振动事件的能量信息，优于传统方法52%以上。该方法在统一连续的幅、时、频域中有效分离噪声，提取振动能量。作为Ф-OTDR振动事件识别的关键参数之一，分析结果对Ф-OTDR的实际应用具有现实意义。

参 考 文 献：

[1] DE VRIES J. A Low-cost Fence Impact Classification System with Neural Networks[C]// IEEE 7th Africon Conference in Africa. 2004， 1：131136.

[2] 罗光明， 李枭， 崔贵平， 等. 分布式光纤传感器的周界安防入侵信号识别[J]. 光电工程， 2012，39（10）：71.

LUO Guangming，LI Xiao，CUI Guiping，et al. The Intrusion Signal Recognition of Perimeter Security of Distributed Fiber-Optic Sensor[J]. Opto-Electronic Engineering， 2012， 39（10）：71.

[3] 冯欣，曾周末， 封皓， 等. 基于小波信息熵的分布式振动传感系统的扰动评价方法[J]. 光学学报， 2013， 33（11）：55.

FENG Xin， ZENG Zhoumo， FENG Hao， et al. Method for Evaluating the Disturbance in Distributed Vibration Sensor Based on Wavelet Information Entropy[J]. Acta Optica Sinica， 2013， 33（11）：55.

[4] TAN Dongjie， TIAN Xiaozhong， SUN Wei. An Oil and Gas Pipeline Pre-warning System Based on Φ-OTDR[C]// Preceedings of SPIE-The International Society for Optics and Photonics， 2014：9157.

[5] ZHU Hui， PAN Chao， SUN Xiaohan. Vibration Pattern Recognition and Classification in OTDR Based Distributed Optical-fiber Vibration Sensing System[C]// Preceedings of SPIE-The International Society for Optics and Photonics， 2014：9062.

[6] 蔣立辉，盖井艳，王维波，等. 基于总体平均经验模态分解的光纤周界预警系统模式识别方法[J]. 光学学报，2015，35（10）：60.

JIANG Lihui， GAI Jingyan， WANG Weibo， et al. Ensemble Empirical Mode Decomposition Based Event Classification Method for the Fiber-Optic Intrusion MonitoringSystem[J]. Acta Optica Sinica， 2015，35（10）：60.

[7] 郑印， 段发阶， 涂勤昌， 等. φ-OTDR识别不同频率振动事件研究[J]. 光电工程， 2015， 42（5）：68.

ZHENG Yin， DUAN Fajie， TU Qinchang， et al. Monitoring Intrusion Incidents in Different Frequencies Based on φ-OTDR[J]. Opto-Electronic Engineering， 2015， 42（5）：68.

[8] 吴俊， 管鲁阳， 鲍明， 等. 基于多尺度一维卷积神经网络的光纤振动事件识别[J]. 光电工程， 2019， 46（5）：79.

WU Jun， GUAN Luyang， BAO Ming， et al. Vibration Events Recognition of Optical Fiber Based on Multi-scale 1-D CNN[J]. Opto-Electronic Engineering， 2019， 46（5）：79.

[9] 盛智勇， 曾志强， 曲洪权， 等， 基于随机配置网络的光纤入侵信号识别算法[J]. 激光与光电子学进展， 2019， 56（14）：47.

SHENG Zhiyong， ZENG Zhiqiang， QU Hongquan et al. Fiber Intrusion Signal Recognition Algorithm Based on Stochastic Configuration Network[J]. Laser & Optoelectronics Progress， 2019， 56（14）：47.

[10]QIN Zengguang， CHEN Hui， CHANG Jun. Signal-to-Noise Ratio Enhancement Based on Empirical Mode Decomposition in Phase-Sensitive Optical Time Domain Reflectometry Systems[J]. Sensors（Basel）， 2017（17）：1.

[11]SOTO， M.， RAMREZ， J. THVENAZ， L. Intensifying the Response of Distributed Optical Fibre Sensors Using 2D and 3D Image Restoration[J]. Nat Commun， 2016（7）：1.

[12]Tabi Fouda Bernard Marie， Dezhi Han， Bowen An. Pattern Recognition Algorithm and Software Design of An Optical Fiber Vibration Signal Based on Φ-optical Time-domain Reflectometry[J]. Applied Optics， 2019， 58（31）：8423.

[13]WANG Zhandong， LOU Shuqin， LIANG Sheng. Multi-class Disturbance Events Recognition Based on EMD and XGBoost in φ-OTDR[J]. IEEE Access， 2020（8）：63551.

[14]SHI Yi， WANG Yuanye， ZHAO Lei. An Event Recognition Method for Φ-OTDR Sensing System Based on Deep Learning[J]. Sensors（Basel）. 2019， 19（15）：3421.

[15]Bernard Marie TabiFouda， Dezhi Han， Bowen An， et al. Research and Software Design of an Φ-OTDR-Based Optical Fiber Vibration Recognition Algorithm[J]. Journal of Electrical and Computer Engineering， 2020（1）：1.

[16]邵巖，卢迪，杨广学，分数阶傅里叶变换在轴承故障诊断中的应用[J]， 哈尔滨理工大学学报2017，22（3）：1.

SHAO Yan， LU Di， YANG Guangxue. Application of Fractional Fourier Transform in Fault Diagnostics of Rolling Bearing[J]. Journal of Harbin University of Science and Technology， 2017， 22（3）：1.

[17]温鹏辉. 基于分数阶傅里叶变换的滚动轴承故障诊断[J]. 内燃机与配件， 2020（5）：1.

WEN Penghui. Fault Diagnosis of Rolling Bearing Based on Fractional Fourier Transform[J]. Internal Combustion Engine & Parts， 2020（5）：1.

[18]纪俊卿， 张亚靓， 孟祥川， 等. 自适应小波阈值滚动轴承故障振动信号降噪方法[J]. 哈尔滨理工大学学报， 2021， 26（2）：124.

JI Junqing， ZHANG Yaliang， MENG Xiangchuan， et al. Adaptive Wavelet Threshold Rolling Bearing Fault Vibration Signal Denoising Method， Journal of Harbin University of Science and Technology， 2021， 26（2）：124.

[19]薛萍， 姚娟， 邹学洲， 王宏民. 基于法矢修正的点云数据去噪平滑算法[J].哈尔滨理工大学学报，2018，23（5）：86.

XUE Ping， YAO Juan， ZOU Xuezhou， et al. Smoothing Algorithm of Point Cloud Based on Normal Vector Correction[J]. Journal of Harbin University of Science and Technology， 2018，23（5）：86.

[20]柳长源， 张付浩， 韦琦. 基于脑电信号的癫痫疾病智能诊断与研究[J]. 哈尔滨理工大学学报， 2018， 23（3）：91.

LIU Changyuan， ZHANG Fuhao， WEI Qi. Intelligent Diagnosis and Research of Epileptic Diseases Based on EEG Signals[J]. Journal of Harbin University of Science and Technology， 2018，23（3）：91.

[21]王海英， 王远远， 姚之琳. 心电信号QRS波检测算法的设计与仿真[J]. 哈尔滨理工大学学报， 2019，24（4）：84.

WANG H， WANG Y， YAO Z. Design and Simulation of Detection Algorithm for QRS Wave of ECG Signal[J]. Journal of Harbin University of Science and Technology， 2019，24（4）：84.

（编辑：温泽宇）