基于场路耦合的电力变压器不同运行方式下漏磁场的仿真研究

王康 曾静岚 郑宇 兰生 杜国安 林野

摘 要：針对变压器运行方式改变，变压器在短路电流的冲击作用下，绕组的磁场分布特性存在差异的问题。本文采用了场路耦合的有限元仿真方法，以1台SSZ11-50000/110三相三绕组电力变压器为研究对象，建立了变压器仿真模型，根据建立的变压器的三维模型，考虑变压器在高-中运行方式下，中压侧绕组出现三相短路故障时，计算出了绕组最大分接、额定分接、最小分接3种情况下瞬态漏磁场，分析了3种不同分接情况下绕组不同位置的轴向、辐向的最大磁感应强度分布规律。仿真结果表明，绕组在短路过程中漏磁场的分布情况与运行状态、时间和空间有关。当t=0.01s，随着短路电流出现最大值，绕组轴向和辐向的瞬态漏磁场数值均为最大，绕组轴向内侧、外侧、中间外侧和辐向顶端和底端漏磁场分布规律差异明显。同时，3种不同分接类型的切换，对高压绕组的磁感应强度畸变影响较大，对中压绕组的磁感应强度畸变影响较小。上述计算结果，可为设计变压器绕组结构提供理论参考。

关键词：变压器;场路耦合; 瞬态磁场;三相短路;有限元仿真

DOI：10.15938/j.jhust.2021.04.005

中图分类号：TM41

文献标志码：A

文章编号：1007-2683（2021）04-0028-10

Abstract：In view of the change in the operation mode of the transformer， under the impact of the short-circuit current of the transformer， the magnetic field distribution characteristics of the windings are different. In this paper， a field-circuit coupling finite element simulation method is adopted. Taking a SSZ11-50000/110 three-phase three-winding power transformer as the research object， a simulation model of the transformer is established. In operation mode， when a three-phase short-circuit fault occurs in the medium voltage side winding， the transient magnetic field leakage under the three conditions of maximum tap， rated tap and minimum tap of the winding is calculated， and the different windings under three different tap situations are analyzed. The distribution law of the maximum magnetic induction intensity in the axial and radial directions of the location. The simulation results show that the distribution of the leakage magnetic field of the winding in the short-circuit process is related to the operating state， time and space. When t=0.01s， as the short-circuit current reaches the maximum value， the values of the transient magnetic field leakage in the axial and radial directions of the winding are both maximum， and the distribution law of the leakage magnetic field in the inner， outer， middle outer and radial directions of the winding axis The difference is obvious. At the same time， the switching of the three different tapping types has a greater impact on the distortion of the magnetic induction intensity of the high-voltage winding， and less influence on the distortion of the magnetic induction intensity of the medium-voltage winding. The above calculation results provide a theoretical reference for the design of transformer winding structure.

Keywords：transformer; field-circuit coupling; transient magnetic field; three-phase short circuit; finite element simulation

0 引 言

由于外界各种因素作用，当电力系统中出现短路状态时，变压器绕组将承受短路电流冲击的影响，因短路电流产生的电动力将对变压器绕组的结构产生严重的破坏，在变压器运行和变压器设计过程中，必须考虑绕组所能承受各种短路电流的作用，从结构上加强变压器绕组强度[1-2]。

目前，针对电力变压器相关的研究主要集中于绕组稳定性及漏磁场的计算和分析，对于变压器磁场的问题，可以结合电磁学理论，运用有限元方法对变压器进行分析和计算[3]。Faiz等对电力变压器绕组所产生的短电流引起的电磁力进行了三维有限元分析研究[4]。G. B. Kumbhar和胡忠平等人，通过场-路耦合研究了变压器绕组的轴向稳定性，并利用理论进行了校核 [5-6]。康雅华等利用三维瞬态场路耦合有限元分析方法计算变压器结构件的三维漏磁场及损耗，以TEAM Problem 21C-M1模型为例，对计算方法进行了验证[7-8]。Ahn等用有限元方法研究了电力变压器的绕组短路状况，并计算了短路的电磁力和通过绕组的浪涌电流 [9-10]。李祎春等利用ANSYS有限元软件，建立低压绕组的结构模型，利用屈曲分析方法分析了低压绕组的辐向稳定性[11]。赵志刚等利用有限元方法计算变压器磁场，并把理论计算结果与220kV变压器的突发短路试验结果作对比，最后分析了变压器低压线圈辐向宽度、导线尺寸、撑条等对变压器抗短路能力的影响[12]。张海军等利用有限元计算了短路电动力的分布规律，进行了多次累积冲击下的变压器绕组结构分析[13-14]。王丰华等使用有限元方法，分析不同预紧力、材料等因素影响绕组轴向的振动特性，并利用实验验证了相关理论[15-17]。汲胜昌等利用ANSYS系列软件对变压器绕组在稳态运行条件下的振动特性进行了仿真计算，并将结果同实测数据进行对比验证，分析了绕组轴向振动特性随其预紧力、温度、老化程度的变化趋势[18-20]。

上述相关文獻的研究，其中一部分研究主要利用理论计算变压器绕组的抗短路能力，其他部分则使用二维和三维有限元模型进行磁场和电动力的仿真分析计算，缺乏对不同分接类型下磁场以及变压器短路过程中的瞬态磁场分布特性的研究分析，而变压器在短路条件下的漏磁场决定了绕组电动力的大小，进而直接影响绕组结构强度，有必要对绕组周围的漏磁场进行分析。本文以1台SSZ11-50000/110电力变压器为研究对象，使用ANSYS系列软件并结合场路耦合理论进行计算，计算出了变压器不同分接下，绕组在短路状态下瞬态磁场强度分布情况，并通过对比研究不同分接下的变压器绕组最大磁场强度分布，得出相关结论，可为绕组的抗短路设计提供参考。

1 磁场计算分析理论

1.1 磁场原理分析

变压器的电磁场分析计算问题，实际上是求解给定边界下的Maxwell方程组问题，而变压器的电磁场有限元求解方法，一般采用节点矢量位磁势法[21]，原理是引入矢量磁位A，将磁场计算转化为求解泊松边值问题：

其中，Ω为求解区域;JSθ表示电流密度JS的分量; Г1，Г2为两种边界条件;Ht表示其切向量;t0为初始时刻。

利用（1）转化为变分函数，进行离散化处理，求解出各节点磁矢量值A。

利用公式B=×Α可计算求解域内任意位置的磁密，其中，x、y方向磁通密度分别为：

1.2 场路耦合计算理论

使用有限元方法计算变压器的电磁场时，通常以电流激励，在实际情况下，变压器外侧的端口一般是电压激励，于是一般引入场路耦合理论，进行有限元计算。对变压器的绕组进行等效，获得场路耦合电路模型如图1所示，利用等效电路与有限元方程进行结合，求解矢量磁位A及磁感应强度B。

忽略变压器绕组中的涡流影响，根据图1可以推出电路方程[21]：

式中：u（t）为电压激励;i（t）为电流;R为电阻;L为电感;e（t）为绕组中的感应电势。

在忽略绞线圈中涡流的情况下，引入矢量磁位A，沿导电回路对电场强度进行积分可以得到电路中的感应电动势为

式中：Sc为绕组截面积;nc为绕组匝数;h为绕组切向的单位矢量。

综合式（3），（4）可得到等效电路方程为

将式（5）表示成矩阵的形式为

式中：U为电压矩阵;I为电流矩阵;L′为电感矩阵。

上述式（6）将磁场与电路联系起来，实现了场路耦合计算。

2 变压器磁场计算算例

2.1 磁场计算过程

根据表1型号为SSZ11-50000/110的电力变压器参数，利用Solidworks建立几何模型，如图2所示。本文考虑变压器在高-中运行方式条件下磁场的分析计算问题，高压侧加载不同分接下的电压，中压侧短路，低压侧开路，三相三绕组变压器被简化成一个三相双绕组变压器。在变压器绕组磁场计算过程作如下假设：

1）忽略变压器绕组的铁芯夹件、压板;

2）忽略变压器绕组的涡流去磁影响;

3）忽略绕组中撑条、垫块等构件对磁场计算的影响。

对变压器磁场计算的材料参数进行设置。绕组相对磁导率1，电导率5×107S/m，变压器的铁芯采用型号35DQ151冷轧硅钢片，相对磁导率由图3所示的B-H曲线设置，铁芯电导率2×106S/m。

根据场路耦合理论，利用ANSYS Maxwell有限元计算软件，对高压侧加载电压，中压侧短路，通过绕组与有限元模型进行耦合计算，计算出变压器绕组的磁场及短路电流。最大运行方式下，场路耦合法的外电路结构如图4所示，高中压绕组为YNyn连接组别，高压绕组设置电压为最大运行方式下的相电压，高压绕组ABC三相电阻R1均为0.89Ω，中压绕组ABC三相电阻R2均为0.16Ω，设置中压绕组短路模拟电阻R3均为1.00×10-10Ω，模拟短路故障;其中，WindingHA、WindingHB、WindingHC，WindingMA、WindingMB、WindingMC分别表示高压、中压绕组的ABC三相，其他运行方式原理相同，只需减少调压绕组线圈个数及匝数。

磁场计算过程中，网格的质量决定了计算的准确性。ANSYS Maxwell有自适应剖分和手动剖分2种形式，本文采用自适应剖分，对不同模块控制网格最大边长进行剖分。其中，最大分接下剖分效果如图5所示，高压、中压绕组最大网格边长为30mm，铁芯最大网格边长为50mm，变压器油介质所在空间区域的最大边长为30mm，自适应的网格总数量为1650089个，能量迭代误差变化率为2.1%，网格总体质量较好。

2.2 短路电流计算结果

利用有限元法进行磁场计算，可得到变压器绕组的3种分接条件下的短路电流如图6所示。3种分接下，在t=0.01s时刻变压器高压、中压绕组的短路电流最大。其中，最大分接、额定分接、最小分接下的高、中绕组短路电流最大值分别为3868.060A、-13.74A，6250.40A、-18693.10A，8585.00A、-22202.50A，結合3种分接下的匝数进行计算，均满足磁势平衡要求。

2.3 瞬态漏磁场计算结果

利用ANSYS Maxwell进行有限元瞬态磁场仿真，取t=0.01s的磁感应强度计算结果，得到最大分接、最小分接、额定分接的磁感应强度图结果如图7所示。对比3种不同分接下的最大磁感应强度可知，最大分接、额定分接、最小分接3种情况下变压器整体的最大磁感应强度为2.77T、3.50T、4.24T。铁芯主要是主磁通，导磁性好，磁感应强度数值大，分布与绕组及周围油介质的漏磁场数值较小，分布相对均匀。

变压器的主磁通和漏磁通路径不同，主磁通主要分布在铁芯中，漏磁通主要分布在绕组及周围介质间隙中。为了研究绕组不同方向的漏磁场分布，于是把变压器绕组空间的漏磁场分布方向分为轴向和辐向2个方向，如图8所示。沿着高压、中压、调压绕组的轴向方向，分别选取3条轴向路径，并计算该3条路径下的轴向瞬态漏磁场分布。考虑最大分接条件下，3条高压、中压、调压绕组轴向路径下的瞬态磁场分布情况，分别如图9～11所示。

对比图9～11中高压、中压、调压绕组的轴向瞬态漏磁场，磁感应强度的第一个峰值是频率为f的暂态周期分量，并随时间逐渐衰减，第二个峰值是频率为2f稳态周期分量，并随时间增大，3条路径下的磁感应强度频率变化相同。

在t=0.01s时，由于高压和中压调压绕组的存在，高压绕组的中间部位出现磁场不平衡，靠近绕组中间部位出现最大值，最大磁感应强度为0.56T;中压绕组在最内侧，绕组磁感应强度分布相对平均，磁感应强度幅值呈现两端小，绕组中间大，最大磁感应强度为1.79T;高压和中压绕组的调压绕组由于中间出现较大空气间隙，空隙的磁感应强度出现极大值，最大磁感应强度为0.86T;中压绕组的磁通密度值大于调压绕组、高压绕组磁通密度。

在图8中选择2条辐向路径：辐向路径1、辐向路径2，计算绕组的瞬态漏磁场如图12、13所示。

对比两条路径下，同一线饼的辐向的磁感应强度随时间变化的趋势与短路电流的趋势一致，数值逐渐减小，且磁感应强度的频率与电动力频率也相同;辐向路径1、辐向路径2下，瞬态磁场变化相似，路径两侧靠近绕组的磁感应强度在t=0.01s达到最大值后开始衰减;由于高压和中压绕组之间存在空道，高压绕组外侧和中压绕组内侧之间的磁感强度“Λ”，铁芯空间的漏磁场呈增加趋势。

2.4 不同分接下静态漏磁场对比

为了分析绕组轴向和辐向的静态漏磁场分布规律，根据前面瞬态磁场的计算结果，取t=0.01s时刻的计算结果，此时短路电流最大，绕组的磁感应强度数值最大。同时，按照图8示意图所示选择路径;其中，沿高压绕组和中压绕组的轴向高度分别取外侧、中间、内侧3条路径作为轴向磁场的计算路径;沿高压和中压绕组顶端和底部的辐向选择2条路径作为辐向磁场的计算路径。

图14、15所示，选择高压、中压绕组顶部和底部的2个辐向路径，绕组顶部和底部漏磁场均呈现中压绕组由内侧到外侧逐渐增加，高压绕组内侧到外侧逐渐减小，绕组中间空道的漏磁场出现一个“平台”，绕组顶部的“平台”比绕组底部“平台”的分布更明显。由于绕组顶部距离变压器铁芯的上铁轭远，空气气隙更大，磁阻大，漏磁通密度明显减小。对比不同分接，最大分接的短路电流最小，漏磁场数值也最小，符合理论。

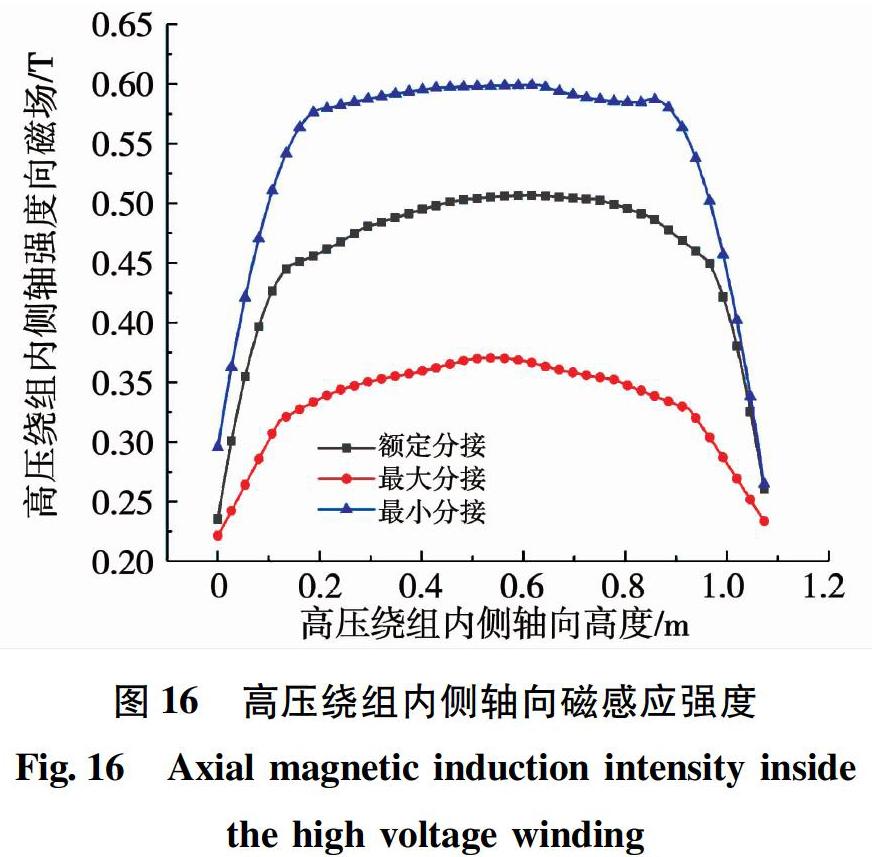
图16～18分别为不同分接下高压绕组内侧、中间、外侧轴向路径下磁感应强度值的分布情况。高压绕组内侧路径靠近空道，不同分接条件下，轴向磁感应呈现“梯形”分布，数值分布呈现两端小，中间大;高压绕组轴向中间路径穿过绕组，轴向磁感应强度呈现“菱形”分布，但是在最大分接条件下，绕组中间磁感应强度出现“凸起”，磁感应强度数值分布规律开始发生变化，受分接类型改变产生了影响;高压绕组外侧路径的磁感应强度分布情况与内侧路径、中间路径不同，轴向磁感应强度呈现“W形”分布，绕组两端和中部磁力线发生弯曲，轴向分量较大。最大和最小分接下高压绕组的漏磁通密度差异明显;最大分接下，短路电流最小，但绕组中部的磁感应强度明显比其他分接更大;由于高压绕组外侧调压绕组的作用，绕组的磁场在中部增大，在轴向漏磁场和短路电流共同作用下，绕组将产生辐向电动力，将更容易对绕组结构产生更强的破坏作用。

图19～21分别为中压绕组内侧、中间、外侧的轴向路径下的磁感应强度分布情况。中压绕组内侧路径靠近铁芯侧，磁力线部分从铁芯中流通，靠近铁芯的上下铁轭的漏磁通密度比中部大，3种分接条件下，轴向磁感应呈现“U”分布，数值分布呈现两端大，中间小;中压绕组中间路径穿过绕组，开始出现畸变，轴向磁感应呈现“W”分布，但在最大分接条件下，绕组中间磁感应强度“凸起”更明显，此时电磁力最大;中压绕组外侧路径，靠近高、中压绕组之间的空道，磁力线中部与绕组轴向平行，两侧发生弯曲，轴向磁感应强度呈现“梯形”分布，数值分布呈现两侧小，中间大，3种不同分接分布规律相似，磁感应强度畸变较小。对比上述6种不同位置高压和中压漏轴向磁场分布情况发现，高压、中压绕组内侧和外侧轴向磁感应强度呈现相反分布趋势，这与绕组之间的空道对轴向漏磁场改变有关。

3 结 论

本文研究了电力变压器绕组在三相接地短路条件下，绕组瞬态漏磁场和静态漏磁场的分布规律。通过使用ANSYS Maxwell有限元仿真软件，利用场路耦合理论，并结合1台110kV电力变压器作为仿真实例，分析了该型变压器的不同空间位置的漏磁场分布，并对比研究了不同分接条件下的最大磁感应强度值，仿真研究结果表明：

1）变压器绕组的轴向和辐向的瞬态漏磁场相对独立，数值大小不同，波形变化规律基本相似，空间分布上存在差异。

2）3种不同分接条件，变压器绕组的短路电流和磁感应强度均在t=0.01s达到最大，其中最小分接条件下，二者数值最大。

3）高压绕组辐向由外侧至内侧，辐向磁感应强度增加，中压绕组辐向由外侧至内侧，辐向磁感应强度逐渐减小，高压和中压绕组之间的空道漏磁场出现极大值，铁芯中间空道漏磁场呈现增加趋势。

4）高压绕组外侧、中间、内侧3个不同位置的轴向磁感应强度分别呈现“梯形”分布、 “菱形”分布、 “W形”分布，分接类型对高压绕组外侧漏磁场分布特性影响最大;中压绕组外侧、中间、内侧3个不同位置的轴向磁感应强度呈现“U”分布、 “W”分布、 “梯形”分布，3种不同分接下磁场分布规律相似，分接类型对中压绕组内侧的漏磁场畸变影响较小。

参 考 文 献：

[1] 张春红， 周腊吾， 李中祥，等. 一起500kV事故变压器短路强度计算与分析[J]. 变压器， 2016， 53（3）：1.

ZHANG Chunhong， ZHOU Lawu， LI Zhongxiang， et al. Calculation and Analysis of Transformer Shortcircuit Strength in a 500kV Accident [J]. Transformer， 2016， 53（3）：1.

[2] 宋云东， 周志强， 张文广，等. 一起变压器绕组严重变形缺陷分析[J]. 变压器， 2019， 56（8）：79.

SONG Yundong， ZHOU Zhiqiang， ZHANG Wenguang， et al. Analysis of a Serious Deformation Defect of a Transformer Winding[J]. Transformer， 2019， 56（8）：79.

[3] 荣佳星， 刘文里， 牛一博， 等. 变压器计及局部安匝不平衡时的轴向动态响应[J]. 哈尔滨理工大学学报， 2017， 22（5）：52.

RONG Jiaxing， LIU Wenli， NIU Yibo， et al. AxialDynamic Response of Transformer Taking into Account Local Ampere-turn Unbalance[J]. Journal of Harbin University of Science and Technology， 2017， 22（5）：52.

[4] FAIZ J ， EBRAHIMI B M ， NOORI T. Three- and Two-Dimensional Finite-Element Computation of Inrush Current and Short-Circuit Electromagnetic Forces on Windings of a Three-Phase Core-Type Power Transformer[J]. IEEE Transactions on Magnetics， 2008， 44（5）：590.

[5] KUMBHAR G B ， KULKAMI S V. Analysis ofShort-Circuit Performance of Split-Winding Transformer Using Coupled Field-Circuit Approach[J]. IEEETransactions on Power Delivery， 2007， 22（2）：936.

[6] 蘭生， 胡忠平， 廖福旺， 等. 短路电动力对变压器低压绕组辐向稳定性的研究[J]. 电机与控制学报， 2018， 22（5）：19.

LAN Sheng， HU Zhongping， LIAO Fuwang， et al.Research on Short-circuit Electromotive Force on the Radial Stability of Transformer Low-voltage Windings[J]. Journal of Electrical Machines and Control， 2018， 22（5）：19.

[7] 康雅华， 白保东， 郭源成， 等. 场路耦合方法在大型电力变压器三维瞬态有限元分析中的应用[J]. 电工技术学报， 2014， 29（9）：219.

KANG Yahua， BAI Baodong， GUO Yuancheng， et al. Application of Field-circuit Coupling Method in Three-dimensional Transient Finite Element Analysis of Large Power Transformers[J]. Transactions of the China Electrotechnical Society， 2014， 29（9）：219.

[8] 朱占新， 谢德馨， 张艳丽. 大型电力变压器三维漏磁场与结构件损耗的时域分析[J]. 中国电机工程学报， 2012， 32（9）：156.

ZHU Zhanxin，XIE Dexin，ZHANG Yanli.Time-domain Analysis of Three-dimensional Leakage MagneticField and Structural Component Loss of Large Power Transformers[J].Proceedings of the Chinese Society of Electrical Engineering，2012，32（9）：156.

[9] AHN H M， LEE J Y ，KIM J K， et al. Finite-Element Analysis of Short-Circuit Electromagnetic Force in Power Transformer[J]. IEEE Transactions on Industry Applications， 2011， 47（3）：1267.

[10]WANG S ， WANG S ， ZHANG N ， et al. Calculation and Analysis of Mechanical Characteristics of Transformer Windings Under Short-Circuit Condition[J]. IEEE Transactions on Magnetics， 2019， 1（7）：1.

[11]李祎春， 刘文里， 唐宇， 等.大型电力变压器低压绕组辐向稳定性分析[J]. 黑龙江电力， 2016， 38（3）：247.

LI Yichun， LIU Wenli， TANG Yu， et al. Radial Stability Analysis of Low-voltage Windings of Large Power Transformers[J]. Heilongjiang Electric Power， 2016， 38（3）：247.

[12]赵志刚， 李光范， 李金忠， 等. 基于有限元法的大型电力变压器抗短路能力分析[J]. 高电压技术， 2014， 40（10）：3214.

ZHAO Zhigang， LI Guangfan， LI Jinzhong， et al. Analysis of Short-circuit Withstand Capability of Large Power Transformers Based on Finite Element Method[J]. High Voltage Technology， 2014， 40（10）：3214.

[13]张海军， 王曙鸿， 李姗姗， 等. 多次短路下电力变压器绕组变形累积效应分析[J]. 变压器， 2018， 55（2）：37.

ZHANG Haijun，WANG Shuhong， LI Shanshan， et al. Analysis of Cumulative Effect of Power Transformer Winding Deformation under Multiple Short  Circuits[J]. Transformer， 2018， 55（2）：37.

[14]张博， 李岩. 多次冲击条件下的大型变压器绕组辐向失稳[J]. 电工技术学报， 2017， 32（S2）：71.

ZHANG Bo， LI Yan. The Radial Instability of Large Transformer Windings under Multiple Shock Conditions[J]. Transactions of the Chinese Society of Electrical Engineering， 2017， 32（S2）：71.

[15]王丰华， 杨毅， 何苗忠， 等. 应用有限元法分析变压器绕组固有振动特性[J]. 电机与控制学报， 2018， 22（4）：51.

WANG Fenghua， YANG Yi， HE Miaozhong， et al. Analysis of Natural Vibration Characteristics of Transformer Windings with Finite Element Method[J]. Journal of Electric Machines and Control， 2018， 22（4）：51.

[16]王丰华， 段若晨， 耿超， 等. 基于“磁–机械”耦合场理论的电力变压器绕组振动特性研究[J]. 中国电机工程学报， 2016， 36（9）：243.

WANG Fenghua， DUAN Ruochen， GENG Chao， et al. Research on the Vibration Characteristics of Power Transformer Windings Based on the “Magnetism-Mechanical” Coupling Field Theory[J]. Proceedings of the Chinese Society of Electrical Engineering， 2016， 36（9）：243.

[17]李洪奎， 李巖. 不同预紧力下变压器绕组轴向振动模态分析[J]. 电机与控制学报， 2010（8）：101.

LI Hongkui， LI Yan. Modal Analysis of the Axial Vibration of Transformer Windings under Different Preload Forces[J]. Journal of Electrical Machines and Control， 2010（8）：101.

[18]汲胜昌， 张凡， 钱国超， 等. 稳态条件下变压器绕组轴向振动特性及其影响因素[J]. 高电压技术， 2016， 42（10）：3178.

JI Shengchang， ZHANG Fan， QIAN Guochao， et al. Axial Vibration Characteristics and Influencing Factors of Transformer Windings under Steady-state Conditions [J]. High Voltage Technology， 2016， 42（10）：3178.

[19]罗汉武， 来文青， 姜国义， 等. 不同温度下变压器绕组材料弹性模量及短路轴向力学性能研究[J]. 绝缘材料， 2017，56（9）：46.

LUO Hanwu， LAI Wenqing， JIANG Guoyi， et al. Research on the Elastic Modulus and Short-circuit axial Mechanical Properties of Transformer Winding Materials at Different Temperatures [J]. Insulating Materials， 2017，56（9）：46.

[20]闫振华， 马波， 马飞越， 等. 220kV电力变压器短路动力学性能分析[J]. 高压电器， 2014（3）：79.

YAN Zhenhua， MA Bo， MA Feiyue， et al. Short-circuit Dynamic Performance Analysis of 220kV Power Transformers[J]. High Voltage Apparatus， 2014（3）：79.

[21]梁振光， 唐任远. 三相电力变压器的场路耦合模型及突发短路过程计算[J]. 电工技术学报， 2004， 19（3）：46.

LIANG Zhenguang， TANG Renyuan. Field-circuit Coupling Model of Three-phase Power Transformer and Calculation of Sudden Short Circuit Process[J]. Journal of Electrotechnical Engineering， 2004， 19（3）：46.

（編辑：温泽宇）