城市轨道交通路网建模中路径搜索算法的实现
2021-10-04何跃齐赵嘉伟
肖 晨,何跃齐,赵嘉伟,张 宁
(1.天津轨道交通运营集团有限公司,天津 300392;2.北京城建设计发展集团股份有限公司,北京 100045;3.东南大学智能运输系统研究中心轨道交通研究所,南京 210018)
1 概述
城市轨道交通具有运量大、速度快、时间准、污染少和安全舒适等特点,在缓解大城市交通拥堵方面具有独特优越性,已成为城市公共交通系统中的重要组成部分。截至2019 年底,中国大陆地区共40 个城市开通城市轨道交通服务,19 个城市进入网络化运营阶段。在网络化运营阶段,客流量急剧增大且乘客出行路径选择增多,需要运营管理者从宏观角度把握客流特征,安排运营组织。构建合理的轨道交通路网模型,能够为运营组织者提供决策依据,而路网模型的关键在于路径选择算法。
以图的方式描述路网已成为交通研究中广泛使用的方法,如何从路网中提取有效路径一直以来都受到广泛关注,相关学者先后提出了Dijkstra 算法[1]、FLOYD 算法[2]、A*算法[3]等一系列最短路径求解方法。然而在网络化运营的轨道交通路网中,起讫点(OD 对)之间可能会存在多条有效路径,如果仅按最短路径进行客流量的分配,会与实际情况有较大出入,故需要求解OD 对间的K 短路径。K短路径搜索问题最早由Hoffman 等[4]提出,并得到不断完善。在轨道交通方面,在找到K 短路径之后,一般情况下,需进一步寻找有效路径进行客流量的分配[5-6]。徐瑞华等[7]通过删除法获得轨道交通网络上任意两点不重复的K 条路径,四兵锋等[8]先利用深度优先的搜索算法,搜索出OD 对之间一条有效路径,接着利用回溯的方法再次进行深度优先遍历,直至找出所有有效路径。这两种方法虽然能够保证搜索路径的完整性,但是复杂程度明显增大,而且在搜索过程中并未对路径进行简化处理,在构建轨道交通路网模型进行客流实时仿真时,可能存在搜索效率不高的问题。周玮腾等[9]对路径做了简化,构建了只包含换乘车站的拓扑网络,利用深度优先的搜索策略搜索出所有有效路径,最后通过对比还原的方法找出完整网络下OD 对之间的有效路径,但是该方法增加了匹配的难度并且没有对搜索深度进行限制,同样会产生一定的无效搜索。本文在简化搜索路径的基础上,利用深度优先的搜索思想并结合轨道交通路网的拓扑特征,提出一种更加高效的有效路径搜索算法。
2 路径搜索算法
2.1 路网模型
本文所建立的轨道交通路网拓扑结构可表示为G={L(s)},G表示所构建的轨道交通路网,L表示轨道交通路网中的线路。其中:
L={l1,l2,…,lm},m为路网中所包含的线路数量;
li={si1,si2,…,sin},n为线路i上的车站数,sin表示线路li上的第n个车站。
车站sin又包含车站名、所属线路编号、车站编号和是否为换乘站点4 个属性。其中,车站所属线路编号为该车站所在所有线路的集合;车站编号由车站在线路上的相对位置确定,按从下行到上行依次递增。换乘站在不同的线路中分别设置不同的编号以示区分。
轨道交通网络由不同的线路组成,各线路间通过换乘车站衔接。本文提出的搜索算法以换乘站为核心节点进行搜索,故需在构建路网模型时,依据车站与线路的逻辑关系,实现如下两个基本方法。
1)寻找与非换乘站最近的换乘站
对于一个非换乘车站,找出其所在的线路上的所有换乘车站,并选择与其间隔车站数最少的换乘站作为其最近换乘站。若同时存在两个或两个以上最近换乘站,则随机选择一个作为其最近换乘站。
2)寻找与换乘站相邻的换乘站
换乘车站是多条线路的交汇点,为保证路径搜索的完整性,需要找出与之相邻的所有换乘车站。对于一个换乘站点,遍历其所在的线路,找出每条线路上与之相邻的换乘车站,形成换乘车站集合,作为与该换乘站相邻的换乘车站。
2.2 限制搜索深度的搜索算法
对于国内大多数轨道交通路网而言,从任意一点出发,最多经过3 次换乘,可以到达路网中任意一个节点。故本文将一个行程分为5 个部分,如图1所示。对于不同的OD 对,换乘站的数目可能有所差别,需要根据实际情况进行调整。在路径搜索的过程中,只考虑由起终点及换乘站组成的简化路网,从给定的起点站开始,通过逐层搜索中间换乘站点的方式,找到与终点站属于同一线路的换乘站以完成路径搜索。同时,为了提高搜索效率,算法限制了搜索深度,搜索到第3 层换乘车站后,如果其不与终点站在同一线路,则放弃该条路径的搜索,这样选择性的放弃了一些明显不合理的路径,节约了搜索时间但不会遗漏合理路径。

图1 出行行程划分Fig.1 Typical travel partition
2.3 算法流程
步骤1:从自动售检票系统(AFC)记录的交易数据中提取乘客出行的起讫点。
步骤2:构建3 个换乘站列表,换乘站列表1、换乘站列表2、换乘站列表3,分别对应如图1 所示的3 个换乘节点。列表为一维列表,用于存放车站(sin)信息,在记录路径时分别称从换乘站列表1、换乘站列表2、换乘站列表3 中提取出的站点为换乘站1、换乘站2、换乘站3。
步骤3:判断起终点是否在同一条线路上,如果是,则记录路径[起点站,终点站],如果不是,则找出与起点站相邻的换乘车站(如果起点站为非换乘车站,找到与之最近的换乘车站,如果起点站为换乘车站,找到与之相邻的所有换乘车站),添加到换乘站列表1 中。
步骤4:遍历换乘站列表1 中的车站,判断其是否与终点站在同一线路上。如果是,则记录路径[起点站,换乘站1,终点站],继续遍历,直至换乘站列表1 中的车站全部被遍历,执行步骤7;如果不是,则中断遍历,找出与之相邻的换乘站,添加到换乘站列表2 中,执行步骤5。
步骤5:遍历换乘站列表2 中的站点,判断其是否与起点站位于同一条线路上。如果是,则将其添加到换乘站列表1 中;如果不是,判断其是否与终点站在同一条线路上,如果是,则记录路径[起点站,换乘站1,换乘站2,终点站],继续遍历换乘站列表2 中的站点,直至换乘站列表2 中的站点均被遍历,清空换乘站列表2、换乘站列表3,返回步骤4 继续遍历下一个车站,如果不是,则中断遍历,继续寻找与之相邻的换乘站并添加到换乘站列表3 中,执行步骤6。
步骤6:遍历换乘站列表3 中的站点,如果其与换乘站1 在同一条线路上,则将此站点添入换乘站列表2,如果其与起点站在同一线路上,则将该站点添入换乘站列表1;否则,判断该站点是否与终点站在同一线路上,如果是,则记录路径[起点站,换乘站1,换乘站2,换乘站3,终点站],继续遍历换乘站3 中的站点,直至列表3 中的换乘站点均被遍历,清空换乘站列表3,返回步骤5 继续遍历下一个车站。
步骤7:输出所有记录的路径。
注1:在步骤4、步骤5 向换乘站列表中添加站点时,如果该站点已经存在于列表中,则不再继续添加。若找到的换乘车站为起点站,同样无需将起点站加入换乘站列表中。
注2:在搜索步骤4、步骤5 中,之所以会往换乘站列表1、换乘站列表2 中回添站点,是为了避免同一线路上出现多个换乘站,导致经过3个换乘站后无法由起点到达终点,即路径中的换乘站指乘客实际发生换乘的车站,而非简单的物理换乘站。
2.4 有效路径筛选
经过上述方法搜索后,某一OD 对之间可能会搜索到多条可达路径,但在实际环境中,乘客在进行路径选择时,不会考虑所有的可达路径,而会从有效路径中进行选择。通常情况下,采用3 条以内渐短路径作为有效路径。故找到可达路径后,还需从中筛选出有效路径,本文考虑设置如下3 条筛选原则。
1)找出搜索结果中经过换乘站数目最少的路径,删除比最少换乘路径多两个及以上换乘站的路径。
2)找出搜索结果中经过车站数目最少的路径,删除路径中经过车站数比最少经过车站数多n个以上车站的路径(n可根据实际调查设定)。
3)如果经1)、2)两条原则筛选过后,剩余路径的条数仍多于3 条,则优先考虑换乘站数较少的路径,换乘站数相同的情况下,保留经过站点数较少或舒适度较高的路径。
3 应用实例
3.1 路网结构设计
以天津地铁为例,首先构建轨道交通路网模型。目前天津地铁包含6 条运营线路,143 个车站及15个换乘车站,在轨道交通路网模型中为每个站点设置包括所属线路、站点编号、是否为换乘站点等3个属性。其中,站点编号由站点在线路上的相对位置确定,从下行到上行依次递增,换乘站在不同的线路中分别设置不同的编号以示区分。
3.2 结果与讨论
以咸阳路站为起始站,以营口道站为终点站,采用本文的搜索方法,共搜索到8 条路径,如表1所示。

表1 咸阳路站至营口道站路径搜索结果Tab.1 Search results of the paths between Xianyang Road Station and Yingkou Road Station
可以看到,此11 条路径均可由咸阳路车站到达营口道车站,但各条路径所经过的站点数及换乘车站的数目不同。根据上述有效路径筛选原则进行筛选,7、9、10、11 号路径为从咸阳路站到营口道站的有效路径,经验证,乘客在出行路径选择时很少会考虑其他路径出行。
评价路径搜索算法优劣主要从准确性与搜索效率两个角度进行考虑,本文使用天津地铁线网客流数据,按上述介绍的算法,寻找全线网20 306 个OD 对之间的有效路径。从准确性角度讲,本文的搜索不会漏掉任何换乘次数≤3 的路径,对有效路径的筛选也满足人们日常出行的行为习惯,算法的准确性可以得到保障。从效率角度讲,本文提出的搜索算法完成全部OD 对的搜索共耗时127 s,找到有效路径210 001 条。相比于基于线路组合的路径搜索算法[10],本文的方法在搜索时间上有明显优势。两种算法的搜索效率对比如表2 所示,可以看到,在路网复杂度明显增大的情况下,本文所实现的方法在搜索时间上仍有明显优势。
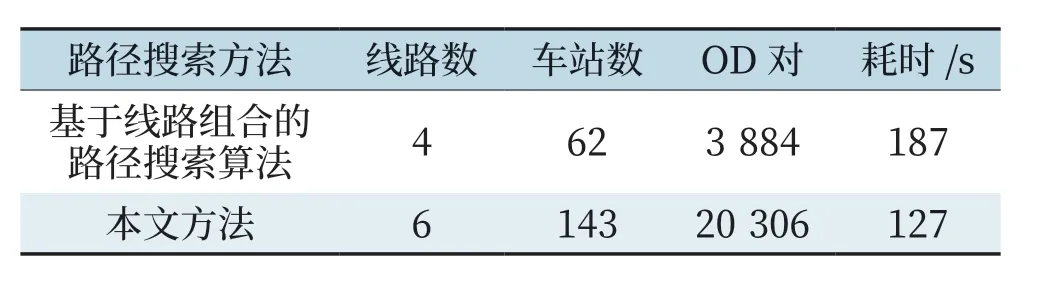
表2 两种搜索算法效率对比Tab.2 Efficiency comparison of two search algorithms
4 结语
本文基于轨道交通线网拓扑特点,利用深度优先的搜索思想,提出了一种高效的路径搜索算法,相比于传统深度优先算法,该算法在搜索之前,首先进行路径简化,减少了搜索节点,同时在搜索过程中,限制了搜索深度,避免无效搜索,大幅提高了搜索效率。此外,本文提出的基于3 层换乘的搜索算法具有良好的可移植性,对城市轨道交通路网模型的建立具有一定的参考价值。
