基于中间估计量观测器的飞行器姿态容错控制
2021-10-01张亮樊承阳周宁博邓双喜银翔叶佳卓
张亮 樊承阳 周宁博 邓双喜 银翔 叶佳卓


摘 要:针对刚性飞行器在飞行过程中发生执行器故障和受到外界干扰的问题,基于中间估计量的方法提出了一种主动容错控制方案。通过设计中间估计量观测器,将常见的乘性及加性执行器故障以整体故障估计量的形式加入到系统模型中,并验证了观测结果的收敛。在未知外部干扰和执行器故障同时存在的情况下,基于求解Riccati方程设计了一种飞行器主动容错控制策略,利用Lyapunov定理验证闭环系统的稳定性。最后通过仿真验证了设计控制系统的有效性和稳定性。
关键词:容错控制;中间估计量观测器;非线性系统;单位四元数
Abstract:An active fault-tolerant control method was proposed based on intermediate estimator for the Aircraft Attitude in the presence of actuator fault and external disturbances. To estimate the total effect of the multiplicative and additive actuator fault instead of each fault individually, an intermediate estimator observer was proposed, and the convergence of the observer's results were verified. To the attitude subsystem with both actuator fault and external disturbances an active fault-tolerant controller based on Riccati equation was designed to track the desired attitude. The stability of the closed-loop system was proved based on Lyapunov's theory. Finally, simulation results show the effectiveness and stability of the proposed control system.
Key words:fault-tolerant control; intermediate estimator; nonlinear systems; unit quaternion
容错控制系统(Fault-Tolerant Control System ,FTCS)作为飞行器的核心安全系统的重要组成部分,用以提高飞行器的可靠性和确保其生存能力[1]。飞行器运行过程中,传感器、控制器、执行器及控制过程本身所存在的微小故障都有可能使整体控制性能受到影响,甚至造成系统的不稳定,进而导致人员和财产的巨大损失[2]。主动容错控制(Active Fault-Tolerant Control,AFTC)在故障发生后能通过实时调整控制器参数和改变控制器结构,更大限度的提高控制系统的性能,更具有应用价值,因此AFTC也受到广泛关注和研究[3]。理想的FTCS是一个能够自动适应组件故障,同时保持整体闭环稳定性和控制性能的控制系统。
现有的FTCS方案通常很难获得故障大小的确切信息。而这些能够准确反映故障的发生、位置以及大小的实时故障估计,对于FTCS而言具有重要意义[4]。近年来对于非线性系统,已经提出不同类型的控制器设计方案:传统PID控制[5]结构简单明了,但需要反复调节PID参数,且应用于非线性系统控制效果有限;文献[6]提出一种基于Lyapunov的反步法姿态控制策略,虽然在有限时间内稳定表现优异,但其鲁棒性较差,需要进行繁琐的补偿;文献[7]提出的自适应控制算法可以动态调节被控对象的参数,但是直接使用标准自适应控制器时,参数选择导致的调节速度过快或过慢,都会影响最终系统控制的表现。
基于上述原因,通过引入中间估计量[8],针对飞行器中常见的Lipschitzian非线性系统故障,基于间接故障识别方法的角速度估计值和辅助参数,得到了影响姿态控制性能的总故障效应,通过Lyapunov定理证明了观测结果的收敛。以此为基础,提出一种基于Riccati方程的飞行器姿态AFTC[9],同样通过Lyapunov定理证明了AFTC系统的稳定性,最后仿真验证结果。
区别于文献[5]和[6]传统容错控制,本文的主要贡献如下:
1)通过引入中间估计量,实现对系统整体故障的估计。相较于传统加性故障与乘性故障的分别估计,本文提出的控制方法在精确实现故障识别的同时,简化了计算流程,提高了系统的可靠性。
2)针对执行机构失效故障,基于求解Riccati方程,设计了故障调节策略,故障时系统能实现对包含非线性和模型不确定的飞行器故障调节,具有良好的动态和稳态性能,三轴姿态角和姿态角速度实现了渐进收敛,能够对系统未建模不确定性、执行器损伤引起的干扰进行及时且有效的容错控制。
1 系统数学模型
1.1 飞行器姿态动力学模型
为避免万向死锁,飞行器姿态的动力学模型可采用单位四元數描述表示为如下形式[10]:
1.2 执行器故障模型
飞行器运行过程中因执行器的老化、元部件失效引起的故障时有发生。根据其故障程度大致可分为执行器卡死、松浮、飞车或饱和以及损伤四种故障类型[11]。执行器故障一般被表示为飞行器模型上的乘性故障Ξ·Γc和加性故障Γadd[12]。
2 中间估计量观测器的设计
1.2节提出的飞行器故障的姿态动力学方程中,对系统总故障f包含加性故障和乘性故障两个分量。考虑到飞行器对姿态控制的时效性要求较高,而目前广泛使用的嵌入式芯片算力有限,针对执行器故障的非线性系统,提出并设计中间估计量观测器,用以实时识别飞行器总体故障。
3 姿态主动容错控制器设计
当运行过程中因执行器的老化、元部件失效引起故障发生后,飞行器正常状态的控制律无法适用于执行器故障模型的控制。为此,本文提出一种基于求解Riccati方程的主动容错姿态控制策略,利用中间量观测器提供的估计角速度i和估计故障,保障故障情况下仍能维持对飞行器姿态的稳定控制。
4 仿真验证
为验证本文提出容错控制算法的有效性,基于Matlab平台对飞行器姿态进行了执行器失效故障情况下的仿真。在对本文提出的容错控制算法仿真验证的同时,设置了如文献[5]中提出的PID容错控制作为仿真对照组。姿态主动容错控制器各项参数设置如下:
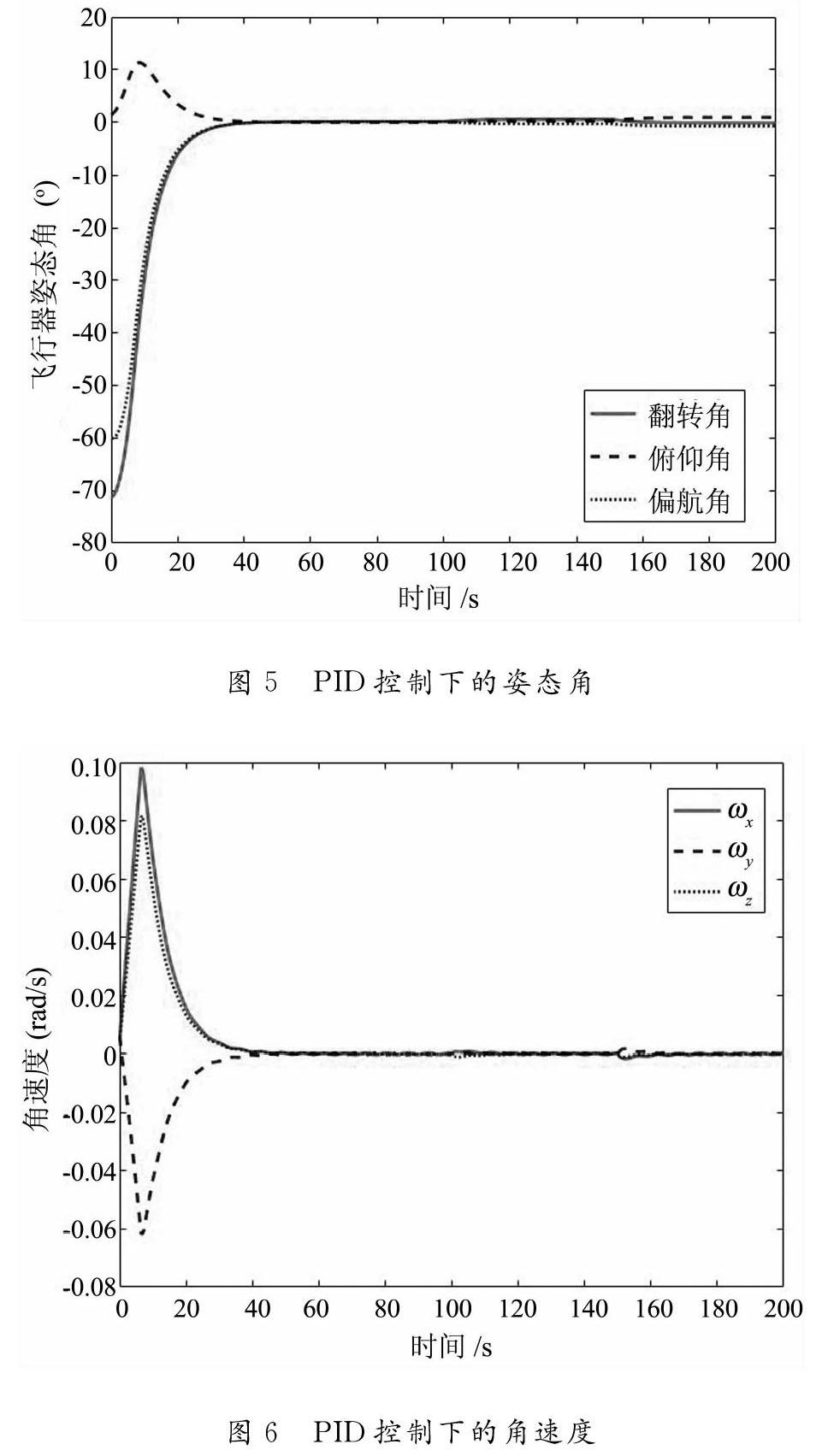
对比图3图5可知,飞行器启动过程中,采用AFTC与 PID容错控制,无论在超调量还是响应时间上都相差无几。但对于t=100 s和t=150 s注入的加性偏置故障,AFTC无稳态误差,能在短时间内对故障进行补偿,进而保持姿态角的稳定,振幅小于0.17°;而PID容错控制出现0.85°的稳态误差,且无法保障姿态角恢复至故障发生前的状态。
同理,对比图4图6,飞行器启动过程中,采用AFTC与 PID容错控制,二者控制性能相当。但对于t=100 s和t=150 s注入的加性偏置故障,AFTC能在短时间内保持角速度的稳定,振幅小于0.00026 rad/s;而PID容错控制虽能保持角速度的稳定,但稳定时间较长(17s)且出现峰值为0.0016 rad/s的误差。
综上,本文采用的AFTC在获得故障估计值后,相较于传统PID容错控制具有良好的动态和稳态性能,三轴姿态角和姿态角速度实现了渐进收敛,能够对系统未建模不确定性、执行器损伤引起的干扰进行及时且有效的容错控制,保证系统在短暂调整后再次满足迹跟踪要求的同时也保障了飞行的安全。
5 结 论
针对同时存在执行器故障和外界干扰的刚性飞行器系统,提出了基于中间观测量的主动容错控制方法,并通过设计中间估计量观测器,将常见的乘性及加性执行器故障以整体故障估计量的形式加入到系统模型中。仿真结果表明姿态主动容错控制能够对系统未建模不确定性、执行器损伤引起的干扰进行及时且有效的容错控制。
参考文献
[1] 邢琰,吴宏鑫,王晓磊,等.航天器故障诊断与容错控制技术综述[J].宇航学报,2003(3):221-226.
[2] 李丽荣,刘春生.基于积分滑模控制的飞行器主动容错控制技术研究[J].电光与控制, 2019, 26(3):20-24.
[3] 韩晓娜,陈朝旭,缑林峰.一类传感器故障的主动容错控制[J].西北大学学报(自然科版),2010,40(1):39-42.
[4] 姜斌,杨浩.飞控系统主动容错控制技术综述[J].系统工程与电子技术,2007(12):2106-2110.
[5] 蒋银行,刘剑慰,杨蒲,等.基于增益调度PID的四旋翼无人机主动容错控制[J].山东科技大学学报(自然科学版),2017,36(4):31-37.
[6] 范佳明,陈奕梅.四旋翼无人机反步自适应容错控制研究[J].计算机仿真,2017,34(7):79-82.
[7] 范佳明,陳奕梅.四旋翼无人机反步自适应容错控制研究[J].计算机仿真,2017,34(7):79-82.
[8] ZHU Jun-wei , YANG Guang-hong , WANG Hong , et al. Fault estimation for a class of nonlinear systems based on intermediate estimator[J]. IEEE Transactions on Automatic Control, 2016, 61(9):2518-2524.
[9] 何斌,芮筱亭,陆毓琪.多体系统动力学Riccati离散时间传递矩阵法[J].兵工学报,2006(4):622-625.
[10]CAI Wen-chuan, LIAO Xiao-hong, SONG Yong- duan. Indirect robust adaptive fault-tolerant control for attitude tracking of space- craft[J]. Journal of Guidance Control and Dynamics, 2008, 31(5) :1456-1463.
[11]XIAO Bing, HU Qing-lei,ZHANG You-ming. Fault-tolerant attitude control for flexible spacecraft without angular velocity magnitude measurement[J]. Guid Control Dyn, 2011,34(5):1556-1561.
[12]姚元鹏.四旋翼直升机控制问题研究[D] .哈尔滨工业大学,2007.
[13]MURUGESAN S, GOEL P S . Fault-tolerant space- craft attitude controlsystem[C].Sadhana-Academy Proceedings in Engineering Sciences, 1987,11(1):233-261,
[14]SHEN Qiang , YUE Cheng-fei , GOH C H , et al. Active fault- tolerant control system design for space- craft attitude maneuvers with actuator saturation and faults[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5):3763-3772.
[15]陈萍.单边Lipschitz非线性系统观测器的设计[J].工业设计,2017(3):182.
[16]闫鑫. 基于滑模的航天器执行机构故障诊断与容错控制研究[D]. 哈尔滨工程大学, 2012.
