塔机臂根铰点水平位移计算方法研究
2021-09-30夏国伟
才 冰,夏国伟,史 勇,吴 静,梅 琨
(抚顺永茂建筑机械有限公司,辽宁 抚顺 113126)
1 塔机臂根铰点水平位移概述
塔机臂根铰点水平位移即塔顶位移(静态刚性)是塔机行业十分关注的问题,历年来在型式试验、现场检验检测、结构设计、用户验收等各个方面都较重视这个参数,已经成为不可或缺的技术指标之一。
我国GB/T 13752-2017《塔式起重机设计规范》标准中5.6.2 条和GB/T5031-2019《塔式起重机》标准中5.2.5 条均对塔机塔顶位移(静态刚性)都做了规定。
早在20 世纪六七十年代,国外塔机理论界就已经提出:只要保持在弹性范围内,保证结构强度、稳定性满足使用要求,刚度主要由结构设计和不同的使用要求决定,塔顶位移并无统一的硬性规定。因为塔机使用的施工领域不同、塔身材料不同、企业加工的精度不同等等,无法达成一致意见。因而在DIN、FEM、BS 等设计规范里,均未对塔顶位移(静态刚度)作出相关规定。因为塔顶位移对塔身产生的附加力矩直接影响塔机强度、结构稳定性、抗倾翻稳定性。因此,塔机设计计算应包括塔顶位移。
塔顶位移的理论定义:塔机不承受横向载荷、塔顶力矩为零时,塔身中心线作为起始原点,额定载荷作用下,塔机起重臂根部连接处相对于无载荷作用时的水平偏移距离。
设塔顶力矩为Mt,塔顶垂直力Pt,塔身垂直力为P0,塔顶位移最大值为Δxmax,Δx由0 趋近于Δxmax,塔顶附加力矩ΔM=[Pt+0.4P0]Δxmax,此式中,0.4P0为考虑塔顶位移导致下面塔身弯曲变形引起塔身的重心变化[3],使塔身力矩增大0.4Δxmax。
塔顶力矩最大值Mtmax

下面讨论塔顶力矩Mt→Mtmax后,对塔身强度、稳定性、抗倾翻稳定性的影响。
1.1 主肢强度
当Δx=0 时,主肢最大轴力

式中MW——风载荷力矩;
MFC——回转离心力力矩;
a——主肢形心线距离。
当Δx→Δxmax,

主肢轴力增大

主肢应力增加值

式中A0——单肢截面积。
塔顶位移使主肢应力增大,是不可忽视的,特别在Δxmax较大时,必须校核应力强度。
1.2 主肢单肢屈曲稳定
为什么仅讨论主肢单肢屈曲稳定?因为塔身桁架结构整体失稳,都是由主肢单肢屈曲失稳而开始的,如实腹结构局部屈曲失稳会导致整体破坏一样。且桁架整体稳定校核计算中很多系数都是来自建筑钢结构,与塔机塔身不符,因此,整体稳定性校核不准确,单肢屈曲稳定校核简单、明确,无论是型材截面积、惯性矩I、回转半径i、长细比λ、屈曲系数φ,均可确切查出。只要保证了单肢稳定性,塔身整体稳定的校核就无必要了。
考虑塔顶位移后,可在强度计算应力除以屈曲稳定系数,即可计算出塔身单肢屈曲稳定性。
当然,由于强度计算应力随塔顶位移增大,而许用应力及φ不变,屈曲稳定的安全裕度肯定降低,因此必须校核单肢屈曲稳定性。
1.3 抗倾翻稳定性
对行走式或压重式塔机,由于塔顶位移,重心变化,稳定性力矩减少,(M+/M-)增加,不利于抗倾翻稳定,应注意校核。
2 塔顶位移的计算方法
除回转支承滚道间隙、连接销轴配合间隙影响外,塔顶位移主要由受载后结构变形所致。当不考虑压弯作用时,塔顶力矩Mt(Nm)、塔顶风剪力Fwt(N)、塔身风载荷分布力W0(N/m)、塔身风载荷集中力Fw0(N)等产生的塔顶位移如图1 所示。

图1 塔顶力矩、水平力产生的塔顶位移
2.1 变截面塔身换算惯性矩
塔身由不同外廓、不同主肢的塔身节组成,例如基础节、过渡节、标准节等。而且他们大多为桁架结构,不是实腹,需要考虑腹杆的影响。惯性矩计算方法如下。
塔身节惯性矩I

图1 中,虚线为位移、细实线为弯矩M、剪力Q,Fw0为基础节、套架的风剪力,则塔身、塔顶风载荷及塔顶力矩产生的总位移ΔM

EI是结构件刚度的重要标志,直接影响塔顶位移大小。对组合塔身的惯性矩不应简单选取。
2.2 不考虑压弯作用时塔身侧向位移计算方法
塔顶位移可以转化为塔身侧向位移,不考虑回转支座、塔头的作用。计算方法毋庸置疑。电算最简单,但是目前电算通用程序存在不能计算屈曲稳定、节点位移不易分析不同载荷产生的位移、不够直观、错误不易检查,而手算简单明了,经得起推敲,便于分析。
本文推荐参考资料1 的手算方法,下面仅对应用此方法做些提示,详细运算过程见资料1,此方法与有限元相比,误差很小。
该方法将塔身按实腹构件求出塔顶位移,即本文ΔM各分项,再乘以考虑腹杆作用的位移修正系数βi,求出ΔM=∑Δi,βi的求法如下
图中,AO——单主肢截面积;——斜腹杆截面积;Ab2——直腹杆截面积。
柔度系数

E——弹性模量。

修正系数

以上是按图2 所示腹杆布置,如与此不同,可参照图表另选,一般,β≥1 修正桁架与实腹位移的不同。

图2 柔度系数及修正系数
在计算ΔM各分项时,I=Ieq,对组合塔身,A0、Ax、An,则按个塔身不同的截面积及B、α等。
2.3 考虑塔身压弯屈曲变形的塔顶位移Δx,欧拉屈曲极限载荷
式中,μ1=2.0,μ2=1.0
塔顶对塔身的垂直力PN

塔顶位移计算值Δx

塔身中部各处位移Δxi

2.4 静位移与动位移
如果外载荷不加动载荷系数,可认为计算的是静位移,反之,则认为是动载荷。静位移测量简单,动位移则应考虑振动效应,频率幅度衰减、加速度,必须具有测试、记录等条件。但在计算方面,也是将动态按静态加动载系数计算,方法相同。
3 塔顶位移计算实例
某塔式起重机,惯性矩I如表1 和图3 所示,塔身由I1/I2/I3组成。图中Ht=75.15m,h1=25.5m,h2=21.75m,h3=13.5m,h4=4.5m。

表1 塔身各阶惯性矩


图3 塔机塔顶位移计算简图
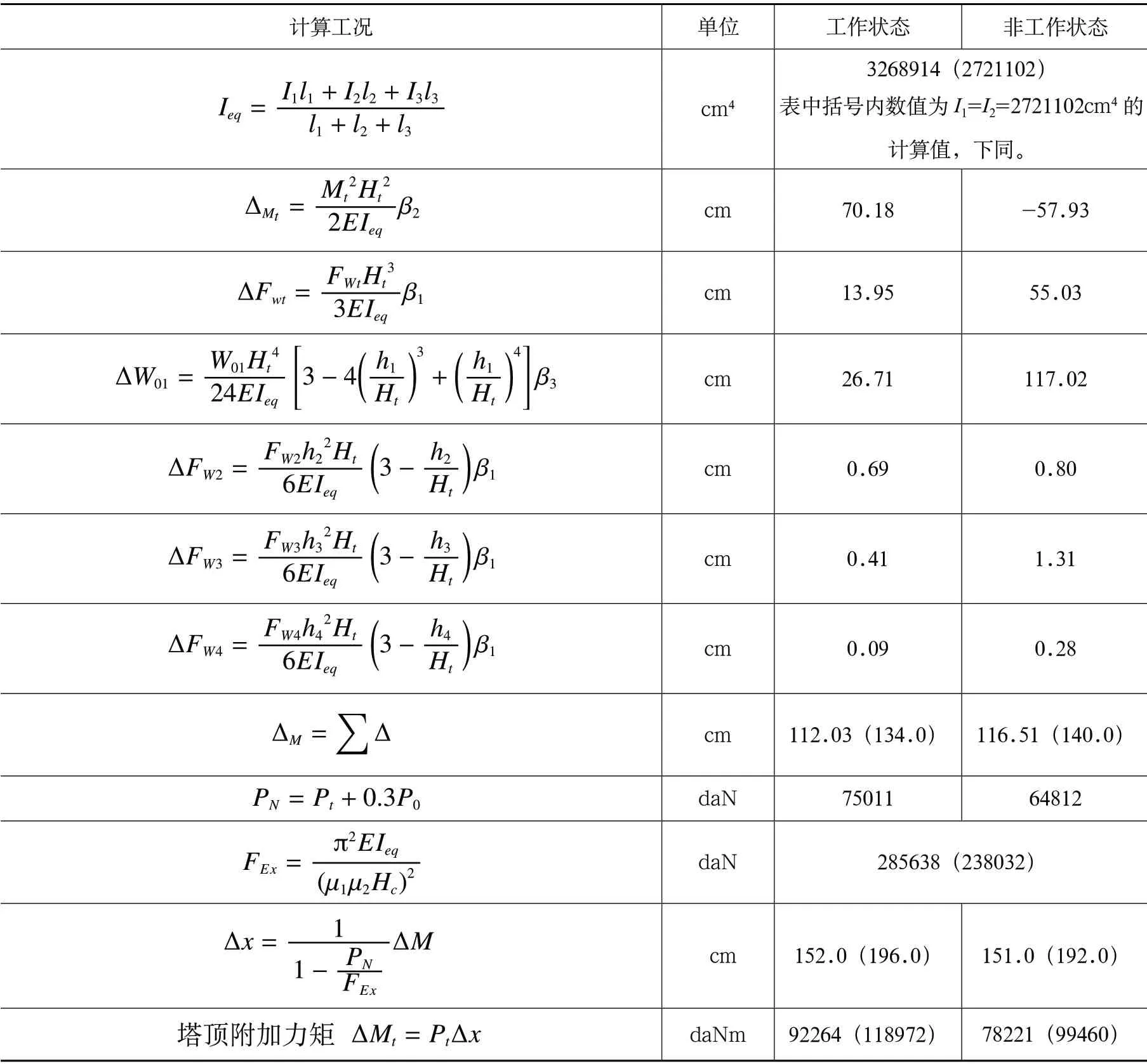
表2 各工况计算数据
4 结语
1)塔身惯性矩对塔顶位移影响很大,选择确定惯性矩尤其重要。
2)塔身惯性矩I=,塔身宽度B占比最大。
3)塔身结构稳定性由单肢来保证,整体稳定校核无必要,建议相关标准应进行明确规定。
4)塔式起重机塔顶位移是塔机设计的重要参数之一,用户对此参数也有高度的重视,建议塔机设计时应予以计算,并且满足相关规范的刚度要求。
