摩擦力对盾构主轴承齿轮啮合的影响

李坤杰，程永龙，何 聪

（中铁工程装备集团有限公司，河南 郑州 461400）

盾构掘进过程中，地层条件复杂且施工过程的多重边界载荷可能使盾构受力载荷发生剧烈波动，很容易导致主驱动系统出现力矩失衡，甚至造成主传动系统力矩不平衡，导致主轴承和小齿轮等关键部件的损坏。一旦关键部件发生破坏，不仅维护成本非常高，而且洞内更换或维修的操作也非常困难，将严重影响盾构施工的经济效益。

主驱动系统是盾构的重要组成部分，主要功能是为刀盘提供切削扭矩，具体路线是将电机或液压马达的原动力通过减速机传递到小齿轮，再通过小齿轮驱动主轴承从而实现刀盘运转。但是，针对复杂的地质情况和工况条件，特别是掘进过程中不规则，强烈冲击以及较大的波动载荷条件，对主轴承齿轮和小齿轮工作时的运行状态有很大影响，主轴承齿轮等关键零部件的极易出现损坏。在主轴承齿轮与小齿轮啮合过程中，齿轮的接触应力过大是造成齿轮传动系统出现故障的主要形式之一。因此，为了提高主轴承齿轮齿的承载能力，确保主驱动系统的安全可靠运行，并延长主轴承齿轮使用寿命，研究摩擦系数对主轴承齿轮啮合过程中接触应力变化的影响具有重要意义。

近年来，对齿轮传动系统的接触问题研究取得了飞速发展，国内外专家学者也对此进行了许多深入的分析和研究，但是，齿轮接触问题的计算通常是基于赫兹公式或基于该公式进行的较小幅度的修改校正，然后通过理论分析获取齿轮啮合传动的接触强度。这样的计算方式结果相对准确，但是计算量大，对于复杂的齿轮传动系统来说，有时甚至无法获得准确的分析结果。与传动的理论计算方法相比，ANSYS 有限元数值分析具有精度高，效率高，方便简单等特点，并直接获得分析结果，更有利于齿轮啮合的相关设计和校对。目前在齿轮系统的研究和分析过程中，很多专家学者虽然对齿轮啮合进行了非常详细的建模和分析，但很少考虑摩擦力对齿轮啮合过程中接触应力变化的影响。由于盾构主轴承在工作过程中的工况条件极为复杂，因此，可以利用ANSYS有限元数值分析方法来更为准确的分析盾构主轴承齿轮在运行过程中的应力和应变变化，在仿真分析过程中增加摩擦系数，分析盾构主轴承齿轮啮合过程中受摩擦力的影响。

为探讨盾构主轴承齿轮和小齿轮在啮合过程中受摩擦力影响的变化情况，本文建立了盾构主轴承和小齿轮的三维模型并进行了有限元分析，找到盾构主轴承齿轮在受摩擦力时的应力和应变变化规律，为提高主轴承齿轮设计制造及啮合受力分析提供理论依据。

1 齿轮接触有限元理论

除了齿轮副的一般弹性方程，盾构的主轴承和小齿轮的啮合传动过程还需要满足啮合点法线上的位移非嵌入条件和库伦摩擦定律在啮合点切线方向上的条件。假设主轴承齿轮和小齿轮都是弹性体，主轴承齿轮为弹性体A，小齿轮为弹性体B，在弹性体A 和B 上的一对接触点分别编号1 和2。如图1 所示，弹性体A 和B 在外部载荷FA和FB作用下发生了位移和。

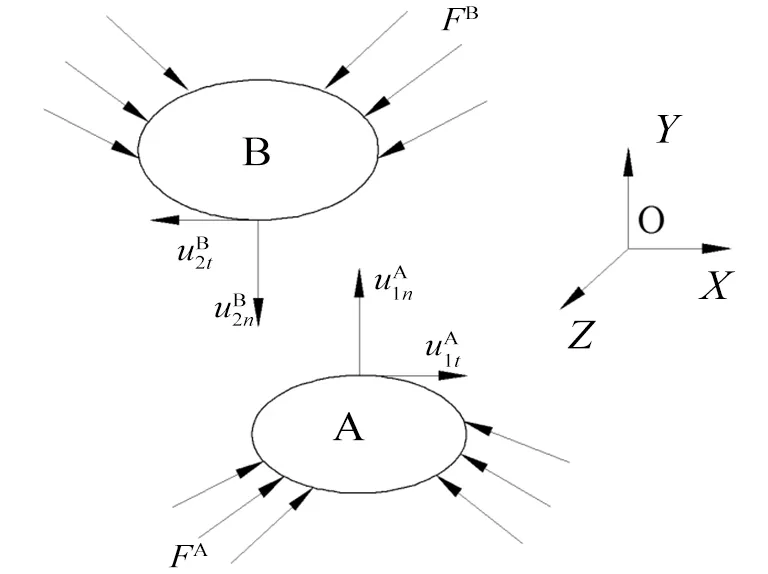
图1 弹性接触体模型

根据有限元的基本理论，其平衡方程为

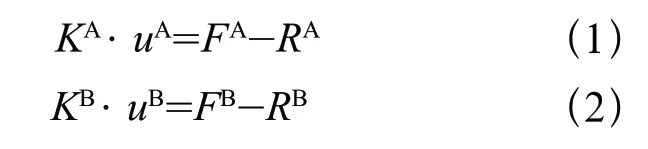
式中KA、KB——弹性体A 和B 的整体刚度矩阵；

uA、uB——弹性体A 和B 的节点位移矢量；

FA、FB——弹性体A 和B 总载荷矢量；

RA、RB——弹性体A 和B 整体接触矢量。

式（1）和式（2）中的KA、KB、FA、FB为已知矢量，uA、uB、RA、RB为未知矢量，假设已经确定了齿轮A 齿轮B 的材料和外部载荷条件，并且假设了A 和B 的单位类型。对于具有确定负责条件的齿轮传动系统来说，齿轮传动系统的啮合情况具有3 种接触状态：连续接触、滑动接触和啮合面的分离。齿轮对的接触边界条件不同，其所对应的接触状态不相同。对于3 种不同接触状态下的定义如下。

连续接触状态

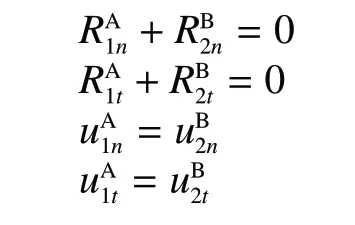
滑动接触状态

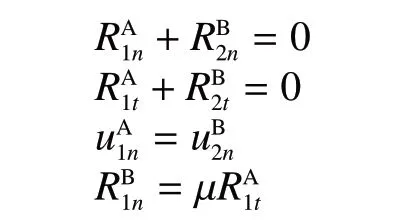
分离状态

可以看出，对于特定的接触状态，假设存在p个接触对，则可以获得4p个条件作为补充方程，并可以求解方程式（1）和式（2）。

2 主轴承齿轮建模及有限元分析

2.1 齿轮建模

本文以某项目主驱动主轴承为例，选择主轴承和小齿轮接触面进行建模和分析，其结构参数如表1 所示。

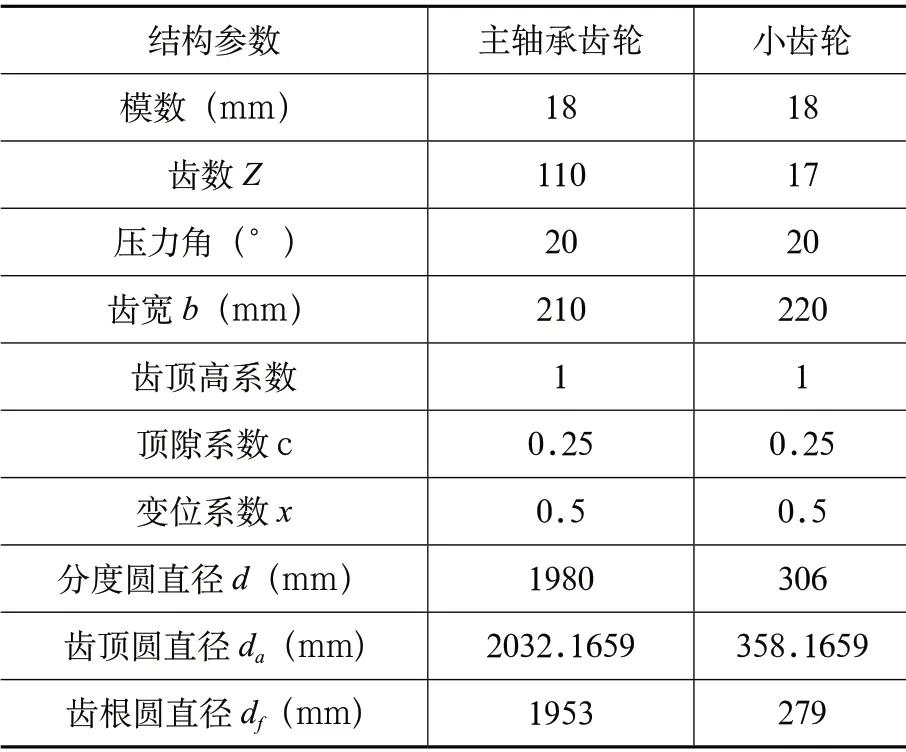
表1 主轴承齿轮和小齿轮基本参数

通过三维软件创建主轴承与小齿轮的啮合模型，将啮合模型导入到有限元分析软件中，并在有限元软件中对啮合模型进行分析。

2.2 ANSYS有限元分析

图2 为盾构主轴承齿轮与小齿轮的三维几何模型，将该模型导入到ANSYS 有限元分析软件中，并通过模拟边界条件和载荷来分析齿轮啮合的应力场。

图2 齿轮三维几何模型

2.2.1 添加材料常数并划分网格

主轴承齿轮材料设置为42CrMo，硬度为HRC55±5，小齿轮材料为17CrNiMo6，齿轮表面作渗碳淬火处理，硬度为HRC58+4，弹性模量E=2.1×106MPa，泊松比λ=0.3，密度ρ=7 930kg/m3。

通过主轴承齿轮有限元分析模型，建立了齿轮啮合的3 个接触对，共有3 对啮合齿和6 个齿轮接触面。在进行有限元分析之前，将盾构主轴承齿轮的摩擦接触类型设计为Fricical，以小齿轮作为驱动轮，主轴承齿轮用作从动轮，对整个模型进行网格划分。

2.2.2 施加载荷和边界条件

在分析齿轮系统的接触问题时，边界条件的定义和负载应尽可能和实际啮合情况保持一致。小齿轮通过与主轴承齿轮啮合传递扭矩，主轴承齿轮在输入扭矩和负载的反作用下保持力平衡，以实现能量传递。将主轴承齿轮（从动轮）内表面设置为固定约束，小齿轮（主动轮）的内孔表面设置为圆柱面约束，并将扭矩和转速等边界条件施加到该内表面。输入转矩为9×107Nmm，小齿轮转速为0.83rad/s。

2.2.3 有限元仿真与分析

在有限元分析中，通过设置摩擦系数，设置边界条件和载荷条件，分析了盾构主轴承齿轮和小齿轮的啮合接触问题。通过应力云图可得摩擦系数为0.1 时，当齿轮接触时，齿轮对的最大接触应力出现在第一对啮合齿上，应力集中主要出现在主轴承齿轮的齿顶处，并且是最大值。当接触齿轮对刚进入啮合时，接触力就相当于是对齿轮施加了剪切力，因此应力集中出现在齿廓的边缘，并且在小齿轮的齿根处也出现了应力集中现象且应力值为最大。齿宽方向上的应力与接触应力呈正比。在齿廓方向上，接触线附近的应力和应变出现最大值。

从盾构主轴承齿轮在啮合时的应变位移云图可以看出，主轴承的齿根或小齿轮的齿顶边缘发生了最大变形，并且小齿轮距离啮合点部位最远的节点的变形最大。

综上所述，主轴承齿轮和小齿轮在啮合过程中，齿轮副的齿根附近的应力和应变有非常大的变化，也是齿轮断齿为何经常发生在齿根处的主要原因。

在恒定负载的条件下，将齿轮的接触类型修改为无摩擦，即齿轮轮齿之间的接触为静态接触。由应力云图得出，啮合齿轮的最大接触应力为276.59MPa，接触变形为0.123mm。在没有摩擦的情况下，齿轮的接触应力和应变大大降低。因此，在有摩擦条件下对齿轮啮合进行有限元分析，研究在摩擦条件下啮合齿轮的接触应力和变形的变化情况以及分析摩擦力对齿轮啮合力变化的影响具有重要的研究意义。

3 结论

1）盾构主轴承齿轮与小齿轮啮合时，应力集中主要发生在轮齿的根部。齿根在啮合过程中最容易出现断裂，这也是盾构主轴承齿轮的主要失效形式。

2）分析了盾构主轴承齿轮和小齿轮的啮合变化情况。通过分析齿轮对在齿轮接触力的作用下最大应力和变形以及危险截面位置等要素，可以为提高主轴承和小齿轮设计、制造及热处理提供理论依据，也为提高齿轮的承载能力和使用寿命提供了可靠的分析方法。

3）主轴承齿轮和小齿轮在工作过程中，摩擦系数的变化对齿轮的啮合接触应力和应变有重要影响。在加工制造时，应充分考虑摩擦力的影响，以延长主轴承与齿轮的使用寿命并提高其承载能力。