失焦照片的去模糊系统设计

闵泳翊 段俊涛

摘要：在日常生活中，我们离不开照片的帮助，照片是我们了解和阅读这个世界的眼睛。而有的时候，照片会因为或相机镜头的粗糙，或拍摄时镜头或者物体的运动，产生模糊的效果。而往往这样的效果，会大大影响照片的质量。而对这些照片进行去模糊的处理，使其重新变得清晰，既能够帮助我们弥补镜头还不够精致的时期的图像的模糊，重现近代的历史或者重现几十年前的情景，又能够提升某些运动情况下图像的清晰状态，从而帮助我们突破一些难以侦破的案件。

关键词：失焦 图像质量 去模糊

1.图像处理概述

在图像处理中，我们一般将模糊图像分为两类：失焦模糊和运动模糊。失焦模糊产生的原因有两种，一种是相机镜头对焦失效导致整个图像的模糊，另一种则是由于镜头内所拍物体距离透镜的不同即景深不同，无法同时对焦多个物体从而导致镜头内部分物体失焦。运动失焦则是在拍摄瞬间镜头的运动或拍摄物体的运动从而导致图像的模糊。在我们拍摄过程中，运动模糊可以通过人为的手段解决，即保持相机与拍摄物体的相对静止，就能够拍出清晰的图像。而失焦模糊往往无法人为解决，只有对拍摄后的图像进行处理。

在本文中，研究的对象是失焦模糊，即对失焦模糊情况下的去模糊处理。失焦模糊的具体表现是图片的背景呈现模糊状态或图片中部分物体呈现模糊状态。要研究失焦模糊，首先要了解光学透镜的原理。根据聚焦的定义，聚焦位置是是最清晰像的位置，即光学透镜焦点所在的位置，当物体通过光学透镜成像时，在焦点位置处观察到的像最为清晰。而如果在焦点前后接收图像，则成像在该平面处不再是一个点，而是光束聚合形成的弥散圆，此时接收到的图像，不再具有在焦点处成像的清晰度。对于具有一定横向宽度的物体，其经过透镜的光线不会聚焦在同一点。而生活中我们拍照时，拍摄的物体往往不会具有到镜头处的相同距离，因此，我们所拍摄的照片都会有一定程度的模糊。

2.图像去模糊处理原理

对于一般的图像，我们都是采用卷积的方式对其进行处理。过程为：

其中，B代表失焦模糊图像，I代表清晰图像，K代表模糊核，N代表图像噪声。模糊核可以理解为矩阵，其本质是通过卷积，对原始图像的每个像素进行模糊处理。而图像噪声则是一切不规则信号，图像在获取过程中会受到噪声的影响。因此，模糊处理的过程需要加上噪声的影响。这里的噪声主要是高斯噪声和椒盐噪声。前者是正态噪声，其概率密度符合正态分布;后者是脉冲噪声，由于传输信息过程中的各种错误缺陷引起。

事实上，不同的图像模糊对应着不同的模糊核。运动模糊中，其模糊核的表达式为

利用相应的模糊核对模糊图像进行处理后，再进行一系列的图像还原，即可完成对图像的去模糊过程。

3.去模糊系统设计

如果我们知道图像的相关模糊核后，我们可以通过反卷积的方法进行图像的清晰度复原，接下来我们进行图像的模糊还原过程。

为获得一个失焦照片，我们选择使用Matlab进行图片仿真，考虑到在失焦模糊中模糊核函数的表达式与Disk模糊中模糊核函数均为弥散圆，在此，我们选择使用Disk模糊代替失焦模糊进行仿真，其中使用Matlab中fspecial函数，该函数是用来生成滤波器的函数，我们使用‘Disk’形式进行原图像处理，使用代码如下所示，对比得到图1。

I= imread（'123123.jpg'）;

figure（1）;

imshow（I）;

title（'Original Image'）;

PSF = fspecial（' disk'，5）;

Blurred = imfilter（I，PSF， 'symmetric’，'conv'）;

figure（2）;

imshow（Blurred）;

title（'Disk Blurred’）;

imwrite（Blurred，’Disk模糊.png'）;

在獲得Disk模糊图像后，我们接下来通过Matlab使用露西理查森算法去模糊复原图像。

露西理查森算法

露西理查森算法是图像复原迭代算法里面的经典算法，该算法是以贝叶斯定理和条件概率为基础实现的，其中

式中： 表示 事件发生的条件下事件发生的概率; 、分别是、事件发生的概率。由于：

将式（5）代入式（6）得：

假设为原始图像，为退化图像，则为原图像的灰度分布 为退化图像的分布，是以点为中心的点扩散函数 。把这些量代入式（7），可得卷积形式为：

式中：是迭代次数，一般选择初始条件为进行迭代，当不断增大时， 收敛于 ，进而可求得图像的近似值。式（8）即为露西理查森算法的迭代公式。

接下来我们使用露西理查森算法进行图像的迭代复原，我们选用迭代8次与18次为例，其中使用代码如下，效果展示如图2。

lucy = deconvucy（Burred，PSF，8）;

figure（3）;

Imshow（lucy）;

title（'Restored Image， NUMIT= 8’）;

imwrite（ucy，' 8次迭代.png'）;

lucy = deconvlucy（Blurred，PSF，18）;

figure（4）;

imshow（lucy）;

title（'Restored Image， NUMIT = 18'）;

Imwrie（lucy，’18次迭代.png'）;

可以将图2中两种迭代情况下所求图片与图1（b）中对比，可以发现图像清晰度具有很大改观，但是与图1（a）中比较时，图像的清晰度并没有达到原图标准，接下来我们考虑使用蒙特卡洛模拟来优化迭代次数。

蒙特卡洛模拟

当所要求解的问题是某种事件出现的概率，或者是某个随机变量的期望值时，它们可以通过某种“试验”的方法，得到这种事件出现的频率，或者这个随机变数的平均值，并用它们作为问题的解。这就是蒙特卡罗方法的基本思想。蒙特卡罗方法通过抓住事物运动的几何数量和几何特征，利用数学方法来加以模拟，即进行一种数字模拟实验。它是以一个概率模型为基础，按照这个模型所描绘的过程，通过模拟实验的结果，作为问题的近似解。

在选择迭代次数时，我们查阅资料大部分迭代次数为50次之内获得最优解，在此我們设计迭代次数50次作为我们迭代的最大值，采用随机选取30数据作为蒙特卡洛选择因子，其中对每次选取的迭代次数值所获得的图像进行一个数据的量化表示，对于在每一次循环下生成的图片，我们选取峰值信噪比与信噪比作为复原清晰度的一个标尺。本文使用Matlab中内置函数峰值信噪比函数进行计算。

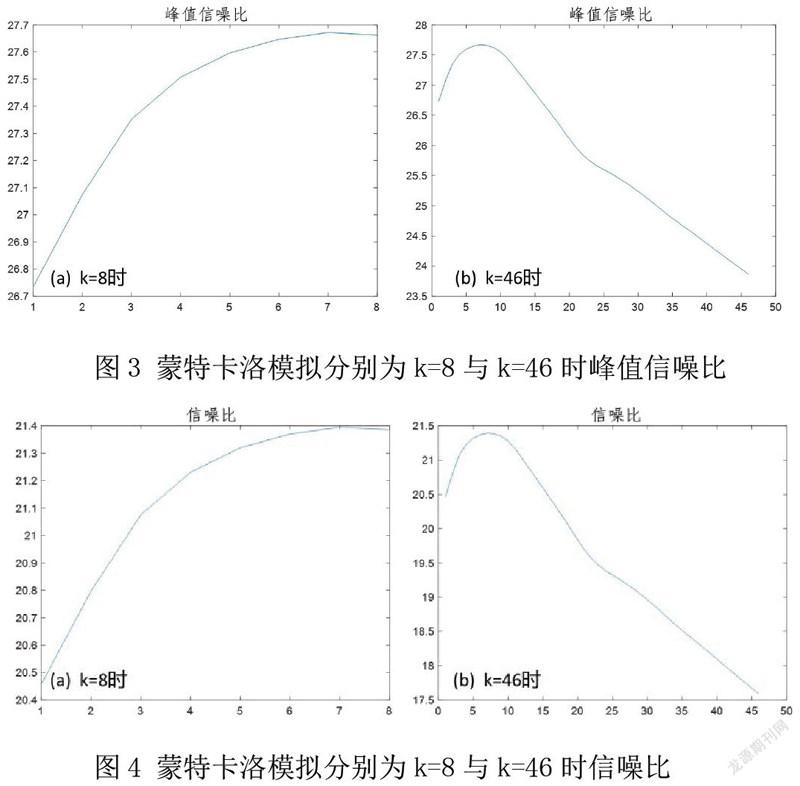
其中考虑到通过峰值信噪比与信噪比大小比较复原清晰度示例如图3、图4。

对比图3中（a）与（b），图4中（a）与（b），可以看出在使用露西理查森算法迭代次数为7次时可以获得最清晰图片，这样也就完成了图像的模糊复原过程。

4.结论与总结

本文提供了一种失焦照片的去模糊设计方案，根据失焦模糊的模糊核对图像进行模糊处理。而后对模糊处理后的图像进行清晰度还原，通过对灰度分布的选取，使用图像迭代算法，还原出相较于原图像更为清晰的图像。同时，在设计中采用蒙特卡洛模拟，使其得到的图像结果为其迭代过程的最优解。

5.参考文献

1.Dowski and Cathey， “Extended depth of field through wave-front coding，” Applied Optics 1995.

2.基于深度全卷积网络的图像可变模糊盲去除，伍处单，华南理工大学，2018-04-20

3.无参考图图像模糊区域分割算法研究，王坤，东南大学，2018-04-01

4.单幅图像去运动模糊研究，刘艳玲，北京交通大学，2017-04-01

5.刘砚一，胡洁，刘红英，线性CNN用于QR码图像去模糊化处理.《CNKI;WanFang》，2012

作者简介：

闵泳翊，男，生于2000年2月，汉族，江苏淮安人，江苏大学本科在读，研究方向：光电信息科学与工程