基于BP神经网络CFRP约束混凝土抗压强度预测

马高 刘康

摘   要：为研究BP神经网络对CFRP约束混凝土抗压强度的预测能力以及神经网络模型的输出性能，在大量的实验数据基础上，建立了CFRP约束混凝土抗压强度的BP神经网络预测模型，探讨了不同数据组合对神经网络模型预测精度的影响;基于神经网络理论，将高精度BP神经网络模型生成了可方便应用的一般公式和简化公式，并与已有经验公式进行了对比分析. 研究结果表明：BP神经网络能够很好地挖掘输入输出参数的数据信息，得到高精度的预测模型;相比于传统回归模型，用purelin代替sigmoid做传递函数推导得到的简化线性方程式仅增加了一项常数项，其预测值与试验值比值的平均值为1.011，变异系数为0.112，具有更高的预测精度和稳定性.

关键词：纤维增强复合材料;人工神经网络;FRP约束;强度模型

中图分类号：TU37                            文献标志码：A

Prediction of Compressive Strength of CFRP-confined

Concrete Columns Based on BP Neural Network

MA Gao1，2，LIU Kang1

（1. College of Civil Engineering，Hunan University，Changsha 410082，China;

2. Hunan Provincial Key Laboratory on Damage Diagnosis for Engineering Structures（Hunan University），Changsha 410082，China）

Abstract：In order to study the predictive ability of BP neural network on compressive strength of CFRP-confined concrete and the output performance of neural network model，this paper establishes a BP neural network prediction model for the compressive strength of CFRP-confined concrete based on a large number of experimental data. The influence of data combinations on the prediction accuracy of the neural network model is investigated. Based on the theory of neural network，the high-precision BP network model is generated into general formulas and simplified formulas for application convenience，and the prediction results of the neural network models and the empirical formulas are compared and discussed. The analysis results show that： BP neural network can well mine the data information of the input and output parameters and obtain a prediction model with  high accuracy; compared with the traditional regression models，the simple linear equation derived by using purelin instead of sigmoid as the transfer function only adds a constant term，and the average value of prediction result/test result is 1.011，and the coefficient of variation is 0.112，showing a higher prediction accuracy and stability.

Key words：fiber reinforced polymer;artificial neural network;FRP confinement;strength model

纖维增强复合材料（Fiber Reinforced Polymer，FRP）以其优越的材料性能可对混凝土提供有效的横向约束，从而提高混凝土柱的承载能力和抗震性能. 随着对FRP约束混凝土力学性能研究的不断深入，国内外已经积累了大量的试验数据和混凝土本构模型[1-3]. Singh和Patra[4]收集了755个试验数据对56个FRP约束混凝土强度回归模型进行了评价，发现部分模型的预测结果偏于保守，按回归方法得到的抗压强度预测值远低于试验数据;而部分回归模型的预测值与试验值之比的平均值高达2.2～3.8，且预测结果变异系数较大. 显然，按传统统计回归方法得到的强度预测模型具有一定的局限性. BP神经网络由于其优异的自学习和自适应能力，具有良好的研究与应用前景. 朱先勇等[5]通过BP神经网络的训练和神经元间连接权值的调整，建立了合金成分与球墨铸铁组织和力学性能的复杂联系. 唐和生等[6]建立了基于人工神经网络的矩形混凝土柱屈服性能的预测方法，发现与经验预测模型相比，神经网络方法吻合程度更高. 在FRP加固混凝土结构方面，也已开展了一些研究[7-9]，均发现BP神经网络能对结果进行很好的预测，具有较强的映射能力.

目前神经网络的研究大多集中在提高预测精度方面，而对于如何把结果形成简单的数学表达式的研究还很少. J？准rgensen等[10]利用BP神经网络原理将压弯荷载作用下钢筋笼增强RC柱承载力预测模型的权值和阈值输出成简单的数学表达式，相比于其他设计公式更加简单、且具有较高的预测精度. Leung等[11]提出一种用图表和修正系数的方式来输出神经网络结果，该方法计算精度较好，但需要查图表，且修正系数公式较为复杂，不便于推广使用. Pham和Hadi[12]用纯线性purelin函数作为BP神经网络的传递函数，相比用logsig或者tansig做传递函数的网络结构，该方法得到的预测精度有所下降，但是能够将神经网络结果输出为简明的线性方程. 此外，由于原始数据可以互相组合形成新的数据输入，不同的输入形式对预测精度存在影响，Elsanadedy等[13]的研究表明原始数据输入形式和数据组合形式不同（如无量纲、几何物理形式等）对FRP约束柱强度预测结果的影响较大.

因此，本文将神经网络方法引入FRP加固混凝土柱抗压强度的研究中，在大量的试验数据基础上，建立各输入参数及组合形式与被约束柱抗压强度非线性映射关系的神经网络预测模型，最后根据神经网络输出结果提出理论计算公式和简化公式，为FRP约束混凝土柱抗压强度模型的研究提供了新的思路.

1   FRP约束混凝土强度模型

现有的FRP约束混凝土抗压强度模型，大多数是基于Richart等[14]针对主动约束混凝土提出的形式（公式（1）），其中k1为约束有效性系数，m为回归曲线的形状参数. 虽然k1、m的取值通过回归分析得到，但其与FRP约束混凝土的力学机理密切相关，较小的k1反应约束的有效性较差，m则与fl / fco的增量对抗压强度的贡献大小相关，一般小于等于1. 一些常见强度模型的k1、m取值见表1.

式中：fcc为FRP约束混凝土抗压强度;fco为未约束混凝土抗压强度;fl为FRP提供的横向约束应力;ffrp为FRP环向抗拉强度;ρfrp为FRP体积配置率;d为混凝土柱直径;t、εfrp、Efrp分别为FRP包裹层总厚度、FRP断裂应变、FRP弹性模量.

除了上述公式中提到的参数外，FRP种类、FRP强度测试方法同样会影响FRP约束混凝柱抗压强度. 比如：约束试件中FRP实际断裂时达到的应力水平要低于FRP条带拉伸试验测得的抗拉强度;生产商提供的材性指标一般高于FRP条带拉伸试验结果.

2   神经网络的建立与训练

2.1   神经网络原理

BP神经网络能够模仿人脑神经元对外部刺激信号的反应过程，基于多層感知器，结合信号正向传播和误差的反向调节，能有效建立用于处理非线性信息的智能化网络预测. BP神经网络由输入层、隐含层、输出层组成，如图1所示，通过改变网络的连接权值和阈值来适应外界环境，达到误差要求，输出最佳预测值. 故BP神经网络具有较强的容错能力、自学习能力和自适应能力.

2.2   试验数据处理与模型建立

由第1节可知，在原始数据收集过程中应该对FRP种类、FRP抗拉强度测定方法进行分组，减少因数据来源不同而带来的误差. 本文利用Sadeghian和Fam[15]收集的251组CFRP约束混凝土圆柱的试验数据，其中CFRP材性均通过条带拉伸试验获得. 原始数据各参数的频率分布直方图见图2，可以发现：各试验数据变量相对集中，分布不均匀，试件直径主要分布于130 ～ 160 mm，原因为标准圆柱体试件（直径150 mm，高300 mm）使用最多;试验中未约束混凝土强度主要为常见强度范围（30 ～ 50 MPa）;FRP断裂应变、弹性模量主要分布于0.5% ～ 1.5%、200 ～ 300 GPa.

由于所收集的数据往往不在同一个数量级，需将所收集的数据映射到[-1，1]之间，即归一化处理. 本文采用的归一化公式为：

式中：xi是归一化后的输入值;x是原始数据;xmax、xmin分别是这组数据的最大值、最小值，具体数值参见表2.

本文按70%、15%、15%将实验数据随机划分为训练集、验证集和测试集.

由于原始数据可以互相组合形成新的数据，不同的组合形式会对FRP约束混凝土强度的预测精度产生影响. 为了得到最优的输入形式，本文考虑以下3种神经网络模型：1）原始数据，即d、t、 fco、εrup、Efrp，记为模型A;2）考虑物理意义，以ρfrp=4t/d、 ffrp=Efrp frup、fco为输入形式，记为模型B;3）无量纲形式，以γ=t/d、 u = ffrp /fco为输入形式，记为模型C. 即

模型A：

fcc = f1（d，t，Efrp，εrup，fco）        （4）

模型B：

fcc = f2（ρfrp，ffrp，fco）        （5）

模型C：

2.3   最优神经网络结构和模型选择

隐含层的神经元采用光滑、可微S型对数函数sigmoid（见式（7）），将神经元的输入范围从（-∞，+∞）映射到（0，1）区间. 本文的训练函数是trainlm函数，即用Levenberg-Marquard（LM）算法随机把输入向量和目标向量划分成训练、验证和测试集，该算法梯度下降快，训练步数少.

由于Hecht-Nielson在理论上已经证明一个隐含层的BP神经网络能够逼近任何区间内的连续函数，所以本文神经网络选用一个隐含层的结构，但隐含层的神经元个数需要试算确定. 大量研究表明，增加隐含层神经元个数可以提高BP神经网络的映射能力，但是神经元数目超过一定值后，网路性能反而降低. 因此，一般采用R值和均方误差MSE（Mean Squared Error）来确定隐含层神经元个数. 图3为A模型在隐含层为7个神经元时的训练集、验证集、测试集和总集经训练后的拟合情况，可见神经网络经过训练能很好地挖掘输入输出参数之间的关系，预测结果与试验结果的相关性趋近于1. 为了得到最优神经网络结构，将不同神经元个数下的R值和MSE值绘于图4. 可见在网络结构为5-8-1时，MSE值较小，预测精度高且稳定，因此模型A的隐含层神经元数取8个.

在最优的神经网络结构下，各模型的FRP约束混凝土抗压强度预测值vpred与试验值vtest之比的统计信息见表3. 从表中可以看出，A模型的平均值为0.993，变异系数为0.083，计算精度高于B、C模型，说明原始参数模型A为最优模型，能够很好地挖掘输入参数与FRP约束混凝土抗压强度之间的非线性映射关系.

2.4   与现有約束混凝土强度模型比较

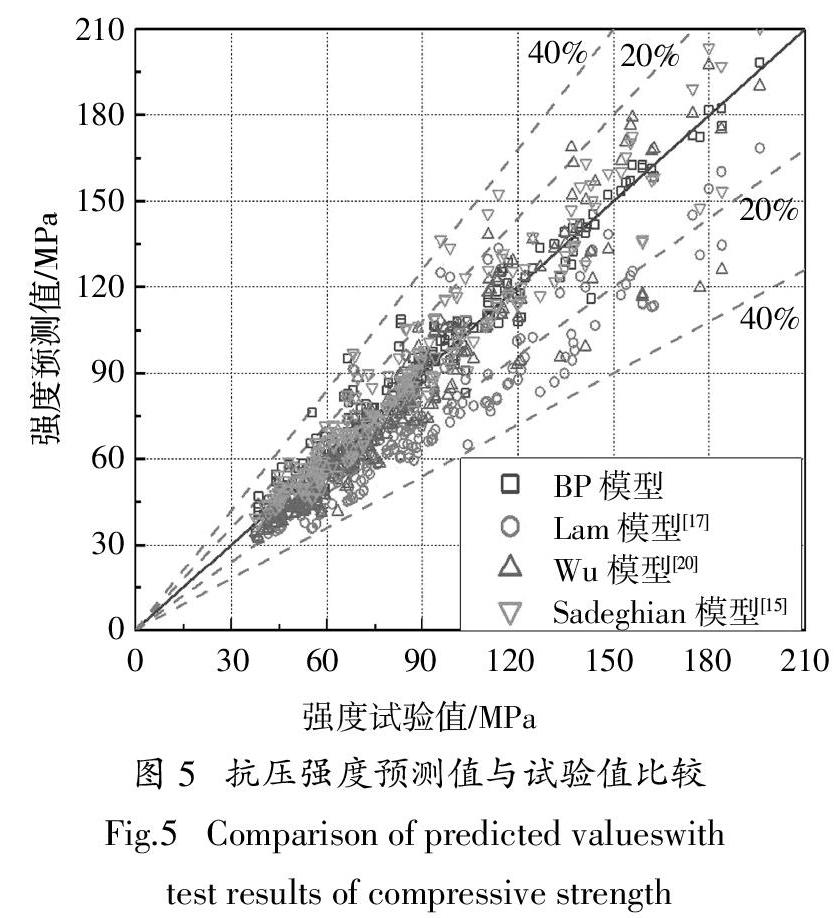
考虑到文献模型提出时依赖的试验数据与本文所用的数据不同，本文选取3个具有代表性的FRP约束混凝土强度模型进行比较，即Lam模型[17]，Wu模型[20]和Sadeghian模型[15]，其中：Lam模型被ACI规范采纳，在研究和工程应用中已被广泛采用;Wu模型为基于大量试验数据的典型非线性模型;Sadeghian模型来自本文引用的数据文献. BP神经网络模型（模型A）、常用强度模型预测值和试验值对比情况见图5和表3、表4.

通过表3可以发现，神经网络模型相比常用强度模型预测精度更高、变异系数更小. 从图5和表4可以发现，各模型误差范围基本都在40%以内，Wu模型、Sadeghian模型和Lam模型的精度依次减小. 神经网络模型中超过90%的数据点误差范围在15%以内，但回归模型误差在15%内的数据点个数不到70%，这说明神经网络模型相比于传统数据回归方法，能够更好地挖掘输入参数的数据信息.

3   神经网络结果公式化输出

神经网络通过不断调整权值和阈值，使网络误差最小或者达到期望要求，因此具有较高的预测精度. 根据神经网络传播理论，可通过权值和阈值输出计算结果. 为便于实际应用，本节将探讨用excel输出网络结果和用简化的线性方程输出改进的神经网络结构.

3.1   理论公式推导

隐含层第i个节点的输入neti为：

式中：iwij表示隐含层第i个节点到输入层第j个节点之间的权值;b1i表示隐含层第i个节点的阈值.

隐含层第i个节点输出ui为：

输出层第k个节点输入netk为：

式中：lwki 表示输出层第k个节点到隐含层第i个节点的权值;b2k表示输出层第k个节点的阈值;φ为隐含层激励函数，即传递函数sigmiod.

输出层第k个节点输出为：

式中：？准为输出层的激励函数，一般为purelin函数：

y = purelin（xi） = xi          （12）

3.2   一般公式结果输出

采用sigmoid做传递函数的模型A的最优网络结构的权重值和阈值见附录A，参照3.1节，因此神经网络隐含层第i个节点输入neti为：

net1=0.249 3x1+0.902 4x2-1.169 8x3+0.705 4x4-

2.092 9x5 - 3.480;

net8=0.882 1x1+1.896 1x2+1.624 8x3+2.759 5x4+

0.447 2x5 - 4.586       （13）

式中：x1，x2，…，x5分别对应d、t、 fco、εrup、Efrp归一化后的值.

传递函数为sigmoid，因此隐含层节点输出ui为：

输出层的激励函数为purelin函数，因此输出层输出为：

y=-3.33u1+2.02u2-0.42u3+3.08u4+2.60u5+

1.15u6-1.50u7-0.79u8-3.17（15）

式中：y是fcc归一化后的结果，可通过反归一化得到fcc，具体参考公式（3）和表2. 基于以上公式推导，利用excel计算表格得到的结果和模型A预测结果完全一致，证明了该公式推导的正确性和神经网络结果输出的可行性.

3.3   简化公式

3.3.1   简化公式推导和模型选择

3.2节中，模型A采用sigmoid函数作为输入层和隐含层间的传递函数时，网络结果需要借助excel等工具辅助输出，不便于推广应用. 因此，本文采用purelin函数代替sigmoid函数做传递函数，期望得到具有较高精度而又形式简洁的线性方程式，其推导过程见图6（以m个参数输入，隐含层为n个神经元为例）.

φ函数采用purelin函数时，式（10）可简化为：

y = lw × iw × x + lw × b1 + b2        （16）

令：

w = lw × iw，a = lw × b1 + b2       （17）

最终计算公式可以写为：

y = w × x + a       （18）

在推导简化公式时，考虑以下3种数据组合形式：

1）模型1. fcc = f1（d，t，Efrp，εrup，fco）

2）模型2. fcc = f2（d，t，Efrp，εrup，fco，fl）

3）模型3. fcc = f3（fco，fl）

对比表3和表5可以发现，未进行数据组合形式下采用纯线性函数purelin做传递函数的模型1比采用sigmoid做传递函数的模型A网络性能差，相关系数R值仅为0.761，但将d、t、Efrp、 输入参数组合成fl后（即模型3），神经网络预测精度明显提高，相关系数R值增加到0.961，这说明：1）数据的不同组合形式对预测精度有影响;2）模型3仅用纯线性函数purelin做传递函数可以得到高精度的预测结果，说明FRP约束混凝土抗压强度fcc与fco、fl近似成线性关系;3）模型2和模型3的区别为：在模型3中，神经网络的训练和学习只能通过改变由d、t、Efrp、εrup组成的fl和fco的权值与阈值来适应，而在模型2中，除fl、fco外，还可调整d、t、Efrp、εrup的权值和阈值，设置模型2是为了得到更高精度的模型. 但对比模型2和模型3结果可以发现，模型2添加d、t、Efrp、εrup后网络模型性能提升并不明显，且本文的模型3已具备较好的计算精度，因此本文采用模型3来推导简化公式.

3.3.2   简化公式结果输出

采用purelin函数的模型3最优拓扑结构为2-7-1形式，此时m = 2，n = 7，将其权重和阈值（附录B）代入式（17），得到

wi = [0.484 4   0.741 9];

a = 0.157 8          （19）

由于式（18）中x、y是歸一化以后的值，为了得到输入参数fl、 fco和输出fcc的相互联系，将归一化式（3）代入（18），得到：

式中：xi为模型3中归一化之前的fl和fco;y1、y分别表示归一化前、后的fcc值;xi max、xi min分别为输入参数最大值和最小值，具体数值见表2.

参考表2及式（19）中的权重和阈值，代入式（24）（25）可得到：

ki  = [0.867 8     2.996 7]

c = 8.552 1

ki中系数称为权重系数，代表各输入参数对输出参数的影响程度.

保留两位有效数字，得到：

fcc = 0.87fco + 3.00fl + 8.55          （26）

3.3.3   简化模型与非简化模型对比

图7和表4对比了各模型预测结果，可见采用purelin做传递函数的简化模型3，相比采用sigmoid做传递函数的BP模型，预测精度有所下降，但下降程度较小;用模型3推导出的预测结果90%以上数据误差在20%以内，相比于回归模型预测精度更高，且变异系数更小.

因此，在使用BP神经网络预测FRP约束混凝土抗压强度时利用purelin函数代替sigmoid函数是可行的，模型3推导出来的线性方程式（式（26））相比于传统回归模型，形式上仅增加一项常数项，但有更高的预测精度，且可以方便实际应用.

3.3.4   简化模型与数据回归模型对比分析

现有的FRP约束混凝土强度模型大多是基于式（1）形式，其k1、m取值依赖于所选择的试验数据. 此外，参考式（26），考虑模型表达式为fcc = Afco + Bfl + C的情况. 对2.2节收集的251组试验数据进行线性回归分析和非线性拟合分析，可得：

式中pred和test分别对应预测值与试验值. IAE和MAPE是对模型误差敏感的统计指标，IAE和MAPE值越小，则模型误差越小. 表6为简化公式与本文回归模型预测结果的统计信息. 可以发现，基于神经网络的简化模型的预测效果仅略低于采用表达式fcc =Afco + Bfl + C直接拟合的结果，但要优于回归模型.

对简化模型的公式变形如下：

式（32）表明约束有效性系数k1是一个变量，随fl增大而降低，对于高侧向约束应力时，k1趋近于常数. 值得注意的是，当fl为0时，式（31）不能退化为素混凝土强度，由于实际应用时FRP约束混凝土均会包裹一定厚度的CFRP（至少一层），因此其约束应力存在最小值.

已有不少文献在基于试验数据的回归分析时，也发现k1不是常数. Balmer[21]发现对于主动约束混凝土，系数k1在4.5到7.0之间变化，平均值约为5.6. Toutanji[22]通过FRP约束混凝土试验结果的对比发现系数k1随fl /fco增大而减小，对于高侧向约束应力时，k1趋近于常数，主要原因是在高侧向约束应力下，混凝土的受压力学行为更接近弹塑性材料，其提出的约束模型公式如下：

fcc = fco + k1  fl，k1 = 3.5（ fl /fco）-0.15       （33）

Fahmy和Wu[23]也报道了相似的结论，且认为FRP约束混凝土强度模型的k1值除了与fl相关，还与混凝土强度有关，其提出的约束模型如下：

k1 = 4.5（ fl ）-0.3，fco≤40 MPa;

k1 = 3.75（ fl ）-0.3，fco > 40 MPa       （34）

4   结   论

现有的FRP约束混凝土抗压强度模型大多是通过数据统计回归分析得到，但是由于FRP约束混凝土柱的力学性能受多种因素影响，各回归模型预测结果相差较大，且有一定比例的数据预测值远大于实验值. 本文在大量的实验数据基础上，用BP神经网络对FRP约束混凝土抗压强度进行预测与分析，发现：

1）BP神经网络模型能够很好地预测FRP约束混凝土抗压强度. 神经网络模型中超过90%的数据点误差范围在15%以内，而回归模型误差在15%内的数据点个数不到70%. 与回归模型相比，神经网络的预测结果精度更高、变异系数更小.

2）基于神经网络理论，将sigmoid函数做传递函数的模型A输出为数学表达式，并生成excel工具表便于实际应用. 利用纯线性purelin函数代替sigmoid函数作传递函数的模型3可生成形式简洁的计算公式，与模型A相比，得到的简化公式计算精度有所下降，但下降程度较小，用模型3推导出的预测结果90%以上数据误差在20%以内，其计算精度仍高于现有的回归模型.

3）仅用纯线性purelin做传递函数的模型3， 其预测结果的相关系数达到0.961，这说明FRP约束混凝土抗压强度fcc与fco、 fl近似成线性关系，且通过权重系数ki能看出横向约束应力fl对FRP约束混凝土强度fcc的贡献远大于未约束混凝土抗压强度fco.

4）神经网络拟合结果是基于已有文献试验数据训练得到的，而非理论推导得到，因此其输出结果的物理意义尚不明确，只具有统计意义. 从统计学角度看，神经网络结果优于常规的线性回归结果.

附录A

神经网络权值和阈值如下：iw是隐含层到输出层的权重值，b1是对应的阈值，lw是输出层到隐含层的权值，b2是对应的阈值.

iw= 0.249 3   0.902 4   -1.169 8  0.705 4   -2.092 9-0.549 9 -0.843 7  -2.030 4  -0.203 1  3.461 0 2.308 6   1.344 1    1.174 9     2.789 4   0.983 8 0.923 7   1.737 3    0.064 6     1.515 2   1.395 9-2.045 9  3.308 3  -0.417 7  -0.419 9  -1.501 5 4.284 8   1.668 3    0.544 7     3.295 7   2.181 2 2.548 7   1.103 0    2.282 6     1.071 8   1.131 9 0.882 1   1.896 1    1.624 8     2.7595    0.447 2，

b1=-3.479 9  3.756 9-1.830 1  0.429 9  1.139 5  2.531 8  2.006 8-4.586 0，lw=-3.325 9  2.022 8-0.421 1  3.081 6  2.603 3  1.148 3-1.500 3-0.787 8，b2 = -3.166 3

附录B

iw=  0.359 6    0.638 2-0.918 9  -0.527 1-0.851 6    0.066 8  0.044 7  -0.022 5-0.807 0    0.963 6  0.637 4    0.249 7  0.633 0    0.639 2，b1=  0.002 4  0.050 5  0.527 1-0.862 3-0.724 9-0.676 9-0.172 7，

lw=  0.779 1  0.393 2-0.692 7-0.310 1  0.229 1-0.177 6  0.454 1，b2 = -0.397 8

参考文献

[1]    滕锦光，陈建飞，林力，等. FRP加固混凝土结构[M]. 北京：中国建筑工业出版社，2005：145—185.

TENG J G，CHEN J F，LIN L，et al. FRP strengthened RC structures[M]. Beijing：China Architecture & Building Press，2005：145—185. （In Chinese）

[2]    马高，陈晓煌. BFRP约束损伤混凝土轴压试验与应力-应变关系[J]. 湖南大学学报（自然科学版），2020，47（1）：36—44.

MA G，CHEN X H. Axial compression test and stress-strain relationship of BFRP-confined predamaged concrete[J]. Journal of Hunan University（Natural Sciences），2020，47（1）：36—44. （In Chinese）

[3]    單波，蔡静，肖岩，等. 大尺寸CFRP约束混凝土方柱的轴心抗压试验研究[J]. 湖南大学学报（自然科学版），2016，43（3）：75—82.

SHAN B，CAI J，XIAO Y，et al. Experimental research on large-scale square columns confined with wrapped CFRP under axial compressive load[J].Journal of Hunan University （Natural Sciences），2016，43（3）：75—82. （In Chinese）

[4]    SINGH S，PATRA N R. Peak strength expression for concrete confined with fiber-reinforced polymer[J]. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems，Part A：Civil Engineering，2018，4（3）：04018024.

[5]    朱先勇，劉耀辉，张英波，等. 基于BP神经网络的球墨铸铁组织和力学性能预测[J]. 湖南大学学报（自然科学版），2007，34（10）：74—77.

ZHU X Y，LIU Y H，ZHANG Y B，et al. Prediction of the microstructural and mechanical properties of pearlite nodule cast iron based on bp neutral network[J]. Journal of Hunan University （Natural Sciences），2007，34（10）：74—77. （In Chinese）

[6]    唐和生，李大伟，苏瑜，等. 人工神经网络预测混凝土柱屈服性能[J]. 湖南大学学报（自然科学版），2015，42（11）：17—24.

TANG H S，LI D W，SU Y，et al. Prediction of the yield performance of RC columns by neural network[J]. Journal of Hunan University （Natural Sciences），2015，42（11）：17—24. （In Chinese）

[7]    陈战波，韩有旺. 神经网络纤维布加固钢筋混凝土梁承载力预测[J]. 山西建筑，2010，36（32）：74—75.

CHEN Z B，HAN Y W. The BP artificial network forecasting model on the load-bearing capacity on reinforce concrete beam strengthened with FRP[J]. Shanxi Architecture，2010，36（32）：74—75. （In Chinese）

[8]    任达，周朝阳，刘坚，等. 带锚FRP受剪加固梁非剥离破坏模式BP网络预测[J]. 土木建筑与环境工程，2017，39（1）：77—85.

REN D，ZHOU C Y，LIU J，et al. Prediction of failure modes for RC beams shear-strengthened with well-anchored FRP composites using neural networks[J]. Journal of Civil，Architectural& Environmental Engineering，2017，39（1）：77—85. （In Chinese）

[9]    任达，黄宝全，刘启华，等. 基于神经网络的FRP抗震加固混凝土柱破坏模式预测[J]. 广州大学学报（自然科学版），2019，18（5）：43—50.

REN D，HUANG B Q，LIU Q H，et al. Prediction of failure modes for FRP-jacketed RC columns under seismic loads based on neural networks[J].Journal of Guangzhou University （Natural Science Edition），2019，18（5）：43—50. （In Chinese）

[10]  J？覫RGENSEN C，GRASTVEIT R，GARZ？魷N-ROCA J，et al. Bearing capacity of steel-caged RC columns under combined bending and axial loads：Estimation based on artificial neural networks[J]. Engineering Structures，2013，56：1262—1270.

[11]  LEUNG C K，NG M Y，LUK H C. Empirical approach for determining ultimate FRP strain in FRP-strengthened concrete beams[J]. Journal of Composites for Construction，2006，10（2）：125—138.

[12]  PHAM T M，HADI M N S. Predicting stress and strain of FRP-confined square/rectangular columns using artificial neural networks[J]. Journal of Composites for Construction，2014，18（6）：04014019.

[13]  ELSANADEDY H M，AL-SALLOUM Y A，ABBAS H，et al. Prediction of strength parameters of FRP-confined concrete[J]. Composites Part B：Engineering，2012，43（2）：228—239.

[14]  RICHART F E，BRANDTZAEG A，BROWN R L. A study of the failure of concrete under combined compressive stresses[R]. Illinois，USA：University of Illinois，Engineering Experiment Station，1929.

[15]  SADEGHIAN P，FAM A. Improved design-oriented confinement models for FRP-wrapped concrete cylinders based on statistical analyses[J]. Engineering Structures，2015，87：162—182.

[16]  SAAFI M，TOUTANJIN H，LI Z. Behavior of concrete columns confined with fiber reinforced polymer tubes[J]. Materials Journal，1999，96（4）：500—509.

[17]  LAM L，TENG J G.Strength models for fiber-reinforced plastic-confined concrete[J].Journal of Structural Engineering，2002，128（5）：612—623.

[18]  SAIIDI S M，SURESHKUMAR K，PULIDO C. Simple carbon-fiber-reinforced-plastic-confined concrete model for moment-curvature analysis[J]. Journal of Composites for Construction，2005，9（1）：101—104.

[19]  MATTHYS S，TOUTANJI H，AUDENAERT K，et al. Axial load behavior of large-scale columns confined with fiber-reinforced polymer composites[J]. ACI Structural Journal，2005，102（2）：258.

[20]  WU Y F，WANG L M. Unified strength model for square and circular concrete columns confined by external jacket[J]. Journal of Structural Engineering，2009，135（3）：253—261.

[21]  BALMER G G. Shearing strength of concrete under high triaxial stress-computation of Mohrs envelope as a curve[R]//Structural Research Laboratory Report No. SP-23. Washington：Bureau of Reclamation，1949.

[22]  TOUTANJI H A .Stress-strain characteristics of concrete columns externally confined with advanced fiber composite sheets[J]. ACI Materials Journal，1999，96（3）：397—404.

[23]  FAHMY M F M，WU Z S. Evaluating and proposing models of circular concrete columns confined with different FRP composites[J]. Composites Part B：Engineering，2010，41（3）：199—213.