MEMS电子罗盘三维补偿线圈参数优化设计

宁治文，傅 军，常 扬

(海军工程大学电气工程学院，湖北 武汉 430033)

MEMS电子罗盘因其具有体积小，成本低等优点，在多传感器信息融合领域有着广阔的应用前景[1]。MEMS电子罗盘主要通过内置三轴磁力计测量地磁分量来解算航向角。除去自身制造安装等方面的误差，在实际导航过程中，三轴磁力计更易受到载体干扰磁场的影响，降低电子罗盘的航向解算精度；强磁干扰严重时甚至超出磁力计量程范围导致其故障失效，进而影响导航系统的整体性能。因此，为提高MEMS电子罗盘的航向解算精度，改善组合系统的导航定位性能，必须对外部干扰磁场进行有效补偿。

磁传感器误差补偿方法主要分硬补偿和软补偿两种[2]。软补偿即通过对磁干扰信息进行数学建模，完成磁力计的校正以及载体硬磁、软磁干扰的综合补偿。通过各种误差建模方法，如椭圆/椭球拟合法进行误差建模，结合最小二乘法进行参数估计，补偿效果良好，但软补偿对建模的精准度要求较高。

硬补偿即通过外加硬件电路，由通电线圈产生补偿磁场以抵消干扰磁场。与软补偿相比，硬补偿方法不需要进行复杂的数学建模，简单有效。文献[3]利用环形线圈实现船舶的快速和高质量退磁。文献[4]分析了线圈位置变化对磁场精度的影响。文献[5]通过高精度电流源控制Helmholtz线圈，用于抵消低频干扰磁场。线圈是补偿磁场的发生部件，设计过程中应当使其既满足磁感应强度的需求，又要有合适的大小，节约制作成本，因此需要通过有限元分析[6]结合相关优化算法对线圈的位置，半径等参数进行优化。文献[7]分析了方形Helmholtz线圈结构特点，通过参数匹配设计了线圈的结构参数；进一步地，文献[8]分析了方形Helmholtz线圈的磁场均匀性，导出了磁场均匀性与线圈结构尺寸的关系式。文献[9]结合改进遗传算法，利用COMSOL有限元仿真，实现了线圈的结构优化。文献[10]通过有限元分析，结合相关优化算法实现了线圈优化。电磁补偿线圈参数的优化设计对有效降低线圈成本，提高磁场补偿精度具有重要意义。

本文从实际应用出发，选取三组互相正交的圆形Helmholtz线圈作为磁场补偿线圈，分别从X，Y，Z三个方向对干扰磁场进行补偿。三维正交线圈可有效避免不同线圈组之间的相互影响。在综合分析了Helmholtz线圈的性能特点的基础上，将线圈半径，线圈厚度与线圈高度作为待优化结构参数。将线圈消耗功率与线圈匝数作为目标函数，通过正交设计方法[11]确定优化初值，选取NSGA-Ⅱ算法和多目标粒子群算法(Multi-Objective Particle Swarm Optimization，MOPSO)进行优化计算。通过仿真对比两种算法，选取线圈最优参数值。

1 线圈建模与算法优化

由于圆形Helmholtz线圈绕制简单，制作成本较低，且MEMS电子罗盘自身体积很小，不需要将补偿线圈尺寸设计得过大，圆形线圈可满足补偿磁场的均匀度需求。因此本文选择圆形Helmholtz线圈作为补偿磁场的发生装置。

1.1 干扰磁场

磁传感器自身的安装误差与制造误差对磁力计的影响较小，便于补偿。通过对称旋转或正交旋转可实现有效的误差校正[12]。当MEMS电子罗盘用于载体导航时，MEMS电子罗盘的主要误差是载体强磁干扰误差，忽略涡流干扰时，主要可分为硬铁干扰与软铁干扰。

在钢制载体的近表面，即使经过消磁处理后，硬铁干扰仍有103nT量级[13]。硬铁干扰主要由导航载体上铁磁性物质的剩磁产生，不管有无外加磁场，剩磁也不会消失，因此可将硬铁干扰视为匀强磁场，补偿也相对简单。软铁干扰即是环境磁场与软磁材料相互作用而产生的感应磁场，该干扰磁场不仅与软磁材料自身特性相关，同时与环境磁场的大小与方向有关。可见在载体坐标系下，软铁干扰磁场将随着载体姿态的变化而变化。假设硬铁干扰为Bp，软铁干扰矩阵Esoft，真实量测磁场为Be，磁传感器输出为Bo，则可将三轴磁传感器载体干扰磁场模型写成如下的矩阵形式:

即:

由此可解出干扰磁场Bd的关系式为:

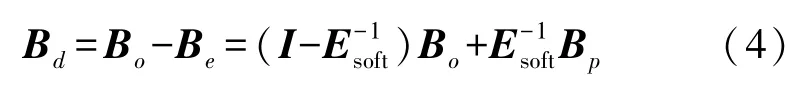
式中:I表示与软铁干扰矩阵Esoft阶数相同的单位矩阵。

1.2 线圈补偿方案

根据毕奥-萨法尔[14]定律，结合叠加原理，空间中单匝Helmholtz线圈轴向某一点A处的磁感应强度表达式可写为:

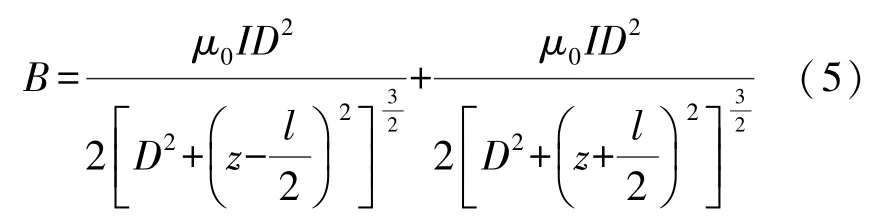
式中:真空磁导率μ0＝4π×10-7H/m，l代表两个线圈之间的距离，z表示A点与两线圈中间点的距离，D表示线圈半径。

在实际应用中，单一线圈无法满足磁场补偿的均匀度，且在线圈绕制过程中由于线径大小的影响，线圈的长度与厚度都不可忽略，因此选取线圈模型为圆柱形，如图1所示。

蓄能器Pacc和发动机泵P1的功率，通过使用功率分流因子概念从P2的预计功率确定.这个概念被选择作为模型的控制输入变量,并且可以在μ∈(-∞,1]范围内变化，则

图1 三轴补偿线圈网格图

用积分法求得单轴(x，y，z)圆柱形亥姆霍兹线圈中心的磁感应强度:

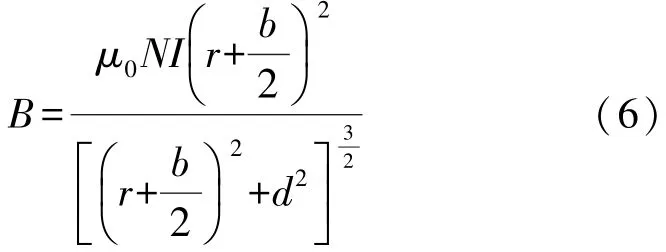
式中:设圆柱形线圈的半径为r，厚度为b，高度为h，2d＝0.5(2r＋b)，d表示一对圆柱形Helmholtz线圈的最佳间距；N表示线圈匝数，若设底层绕线匝数N1＝h/d0，绕线层数K＝b/d0，选取线径d0＝1 mm的导线，则可将绕线匝数N的表达式进一步写为:

以电流I作为线圈激励，通过控制电流的变化调节补偿磁场的大小。理想情况下，若三维圆柱形Helmholtz线圈产生的补偿磁场恰好能抵消三轴磁传感器的干扰磁场，联立式(4)可得到以下补偿电流关系式:

式中:Bd表示各方向的干扰磁场分量。由式(8)可知，线圈补偿电流不仅与外部干扰磁场有关，也与线圈的半径r，厚度b，高度h直接相关。因此，在降低线圈成本的同时保证磁场补偿精度，需要对线圈各参数进行优化设计。

1.3 多目标优化算法

与单目标优化问题不同，在多目标优化问题中，各目标函数之间可能彼此冲突，由此导致了多目标优化问题存在多个最优解，从而形成一个最优解集[15]。法国经济学家Pareto提出了Pareto最优解集概念:在可行域内，不存在另一个解向量满足所有目标函数值均小于(或最大)最优解所对应的目标函数值[16]。即要求所有目标函数都能取得最小值。

NSGA-II算法是非支配排序遗传算法的改进，该算法引入了快速非支配排序方法，精英策略选择方法和拥挤距离参数[17]。快速非支配排序算法提高了多目标函数值的求解效率；精英策略方法扩大了不同个体在概率计算中的差异性，优先保留较优个体，以此将保留的个体作为新一代种群，直至产生最优解；拥挤距离参数则无需用户自定义任何参数，使各组非支配解在Pareto最优方向的均匀分布趋于多样化。

多目标粒子群算法(MOPSO)同样根据支配关系选择Pareto最优解到非支配解储备集，使种群向最优方向前进[18]。通过引入自适应网格方法，根据拥挤程度选取最优个体，来保证其最优解分布的多样和均匀性。

提高磁场的补偿精度，补偿电流的精准控制至关重要。文献[19]提出一种自适应电流控制算法，通过控制线圈的补偿电流实现高精度强磁补偿。因此，本例在定义优化模型时考虑线圈的安装制造与消耗热量。将三轴线圈半径r，线圈厚度b，线圈高度h定为优化变量，选择线圈消耗的总功率与线圈总匝数作为目标函数，优化模型定义如下:

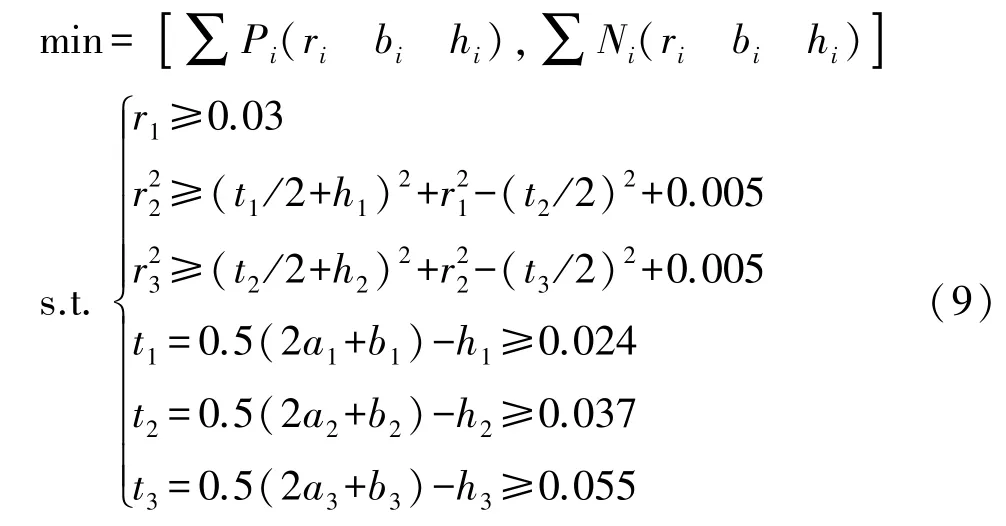
式中:Pi为各个轴向线圈所消耗的功率，约束条件为线圈内部有效容纳空间以及三组线圈正常装配关系，避免线圈在装配时出现相交。t1×t2×t3表示三维线圈内部可容纳空间，本例中该数值的具体大小由MEMS电子罗盘尺寸决定。

2 优化初值选取

2.1 正交试验

线圈各参数初值的设定很大程度上会影响最终优化结果，本文选用正交试验方法确定各优化参数的初值[20-21]。以线圈半径r，线圈厚度b，线圈高度h作为正交试验的3个因素，同时设定v为空白误差项，选取Helmholtz线圈中心处磁感应强度为考核指标。以x轴线圈为例，设置线圈电流为1 A，3个水平取值如表1所示，根据MEMS电子罗盘实际尺寸设置正交试验参数表L9(34)，如表2所示。

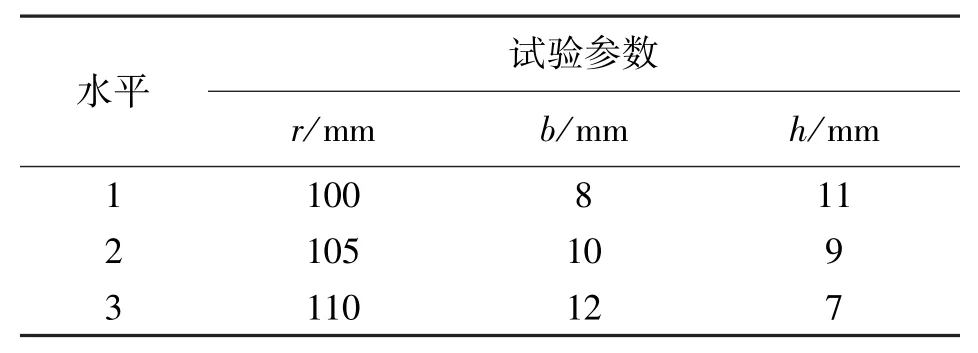
表1 正交试验水平值及参数

表2 正交试验仿真计算结果

极差分析结果如表3所示。

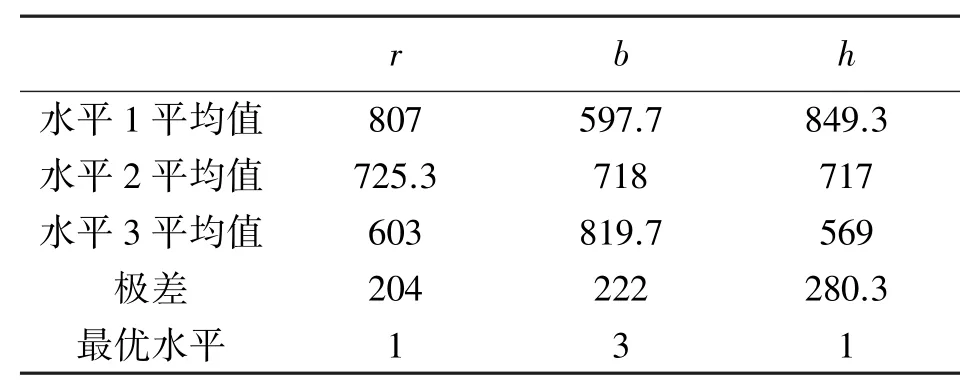
表3 极差分析结果

由表3可知，极差的大小顺序为h>b>r，说明线圈参数对中心磁感应强度影响最大的是线圈高度，其次为线圈厚度，影响最小的是线圈半径。选定x轴线圈各参数初值为线圈半径r＝100 mm，线圈厚度b＝12 mm，线圈高度h＝11 mm。

2.2 有限元分析

根据上述正交试验方法，完成三维线圈参数的初步设置，并在COMSOL软件环境中进行线圈3D建模。各参数初值如表4所示。

表4 三轴Helmholtz线圈仿真模型参数初值

完成线圈建模后进行仿真计算。由于三组线圈由内向外嵌套装配，且每组线圈相互正交，每组线圈所产生的补偿磁场主要作用于该线圈所在轴方向，对其余两坐标轴方向的影响可忽略不计，因此中心处的磁场强度可通过矢量叠加法则进行计算。图2显示三轴中心磁感应强度约为4.1 mT，半径15 mm的球型区域可视为匀强磁场区域。进一步地，分析三维立体以及各平面内的磁感应强度分布，图3(a)显示了三维线圈空间磁场的梯度分布，由图3(b)~图3(d)可知，中心区域颜色均匀统一，且箭头指示方向一致，表示中心区域的磁场大小和方向均不变。

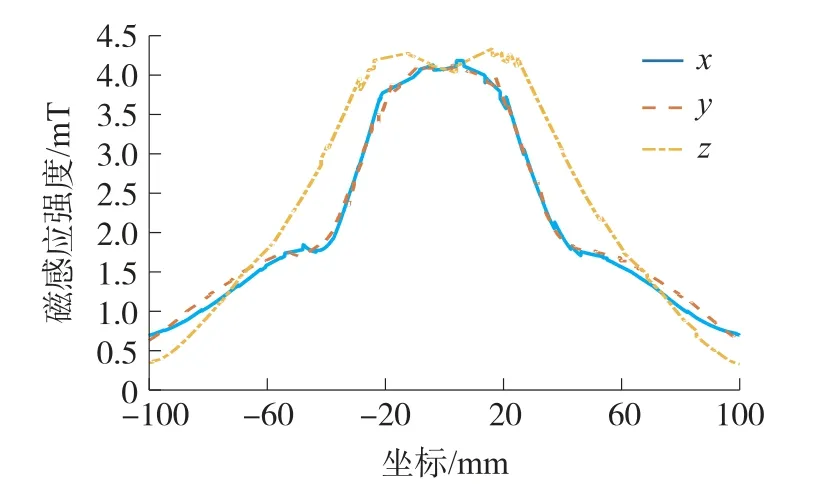
图2 各轴向磁感应强度分布

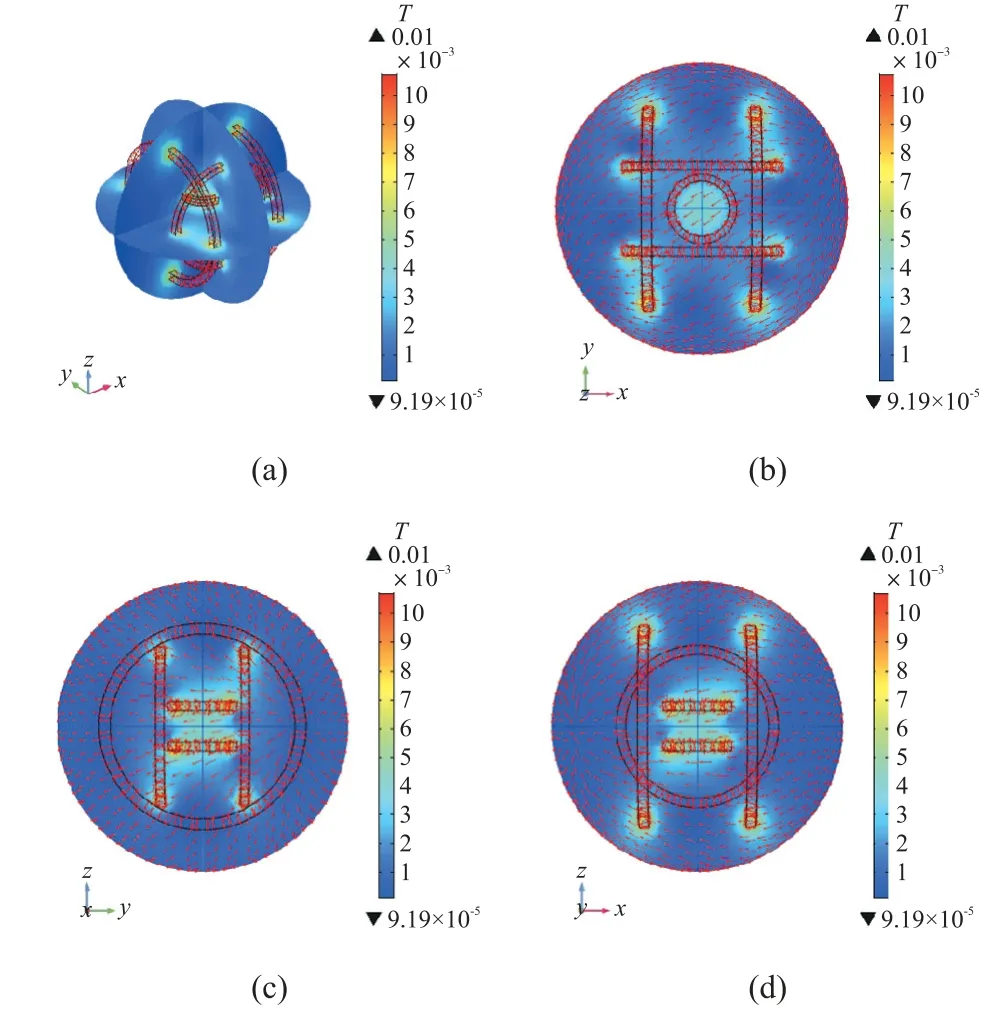
图3 线圈空间及各平面磁场梯度分布

综合分析以上仿真结果可知，该三维补偿线圈结构能满足MEMS电子罗盘强磁补偿需求。

3 参数优化分析

3.1 算法优化结果

以表4中各参数值作为优化初始值，此时电流大小设置为500 mA。分别利用NSGA-II与MOPSO优化算法对线圈结构参数进行优化。NSGA-II算法参数设置:最大迭代次数500，种群规模300，交叉概率0.8。MOPSO算法参数设置:群体大小300，最大迭代次数500，学习因子2.05。两种优化算法所得到的Pareto最优解分别如图4、图5所示。

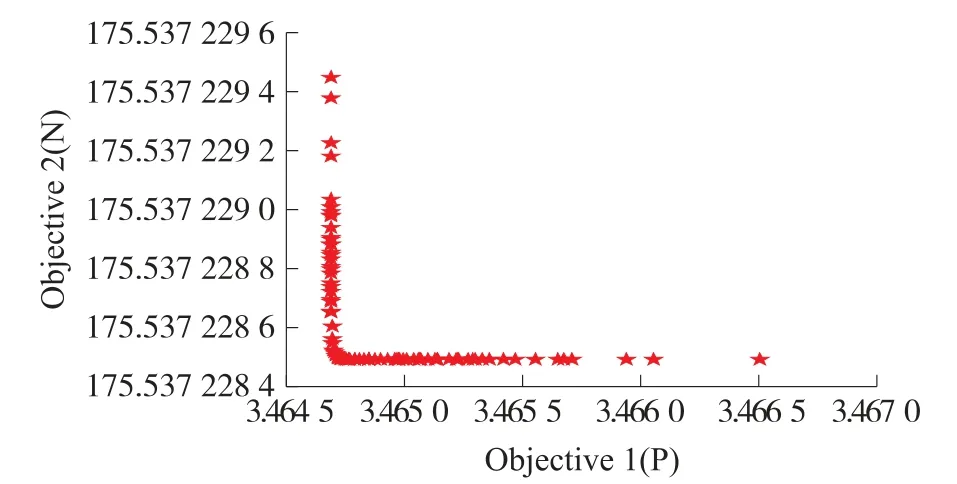
图4 NSGA-II算法Pareto最优解

图5 MOPSO算法Pareto最优解

在NSGA-II算法最优解中，线圈消耗功率约为3.46W时，线圈总匝数约为176匝；MOPSO算法最优解中，线圈消耗功率约为3.48 W时，线圈总匝数约为177匝。虽然两种优化算法得到的目标函数最优解大体一致，但在NSGA-II算法中两个目标函数的冲突性较小，这是由于NSGA-II引入了精英策略选择方法，保留了每代支配等级较高的个体。

将两种优化算法的Pareto最优解代入线圈模型中计算，可得到三轴补偿线圈的优化解。根据线圈半径r，线圈厚度b，线圈高度h3个参数可解出其余的电学参数，对相关参数进行取整后，结果如表5和表6所示。

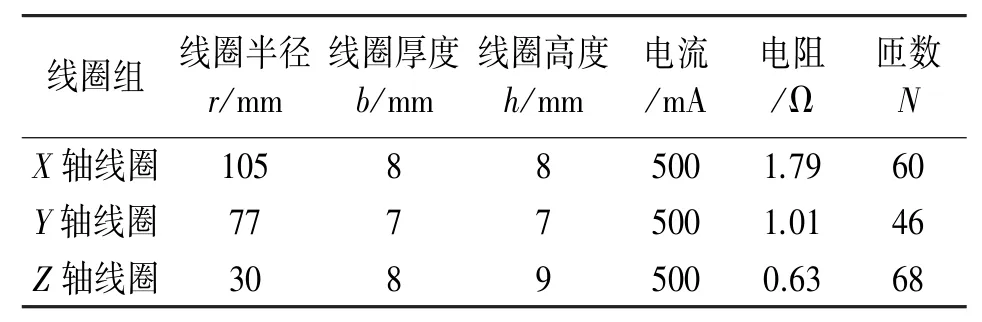
表5 三轴Helmholtz线圈优化参数(NSGA-II)

表6 三轴Helmholtz线圈优化参数(MOPSO)

由表5和表6可知，两组优化参数得到的性能指标相似，均满足补偿线圈设计要求。因此，根据两组参数对线圈进行仿真设计，进一步确定线圈的最终参数。

3.2 实际参数确定

分别以两组数据在COMSOL环境中进行线圈建模，为更好地体现线圈性能，在结果后处理中绘制各组线圈径向截面上的磁感应强度云图。各轴向方向的Helmholtz线圈空间磁场仿真结果如图6~图8所示。

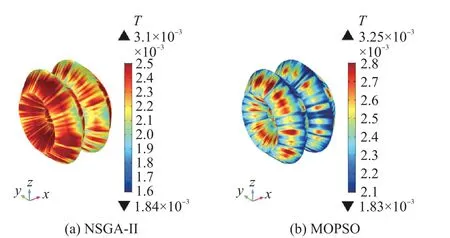
图6 NSGA-II(左)、MOPSO(右)X轴线圈磁感应强度云图

图7 NSGA-II(左)、MOPSO(右)Y轴线圈磁感应强度云图

图8 NSGA-II(左)、MOPSO(右)Z轴线圈磁感应强度云图

分析补偿线圈对应的磁感应强度云图可知，云图中心存在平坦区域，该区域即为匀强磁场区。各线圈在通入相同大小的电流时，两组参数对应的X轴线圈与Z轴线圈的空间磁感应强度分布相似，但MOPSO算法构建的Y轴线圈可产生更强的补偿磁场，拥有更高的补偿效率。

考虑到补偿磁场的均匀性，进一步分析两种算法对应线圈的轴线磁感应强度分布，结果如图9、图10所示，以线圈中心区域磁感应强度的均方根误差(RMS)衡量磁场的均匀性，结果如表7所示。

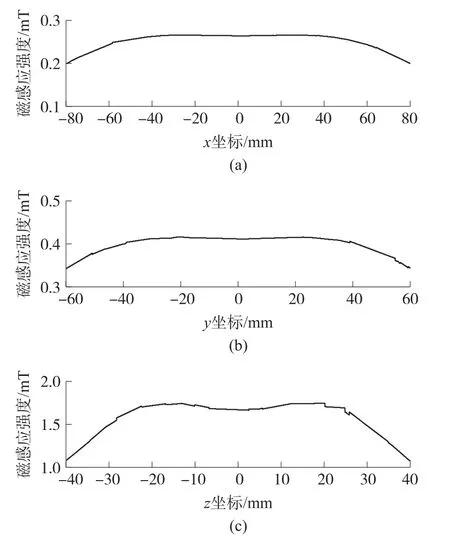
图9 线圈(NSGA-II)磁感应强度分布

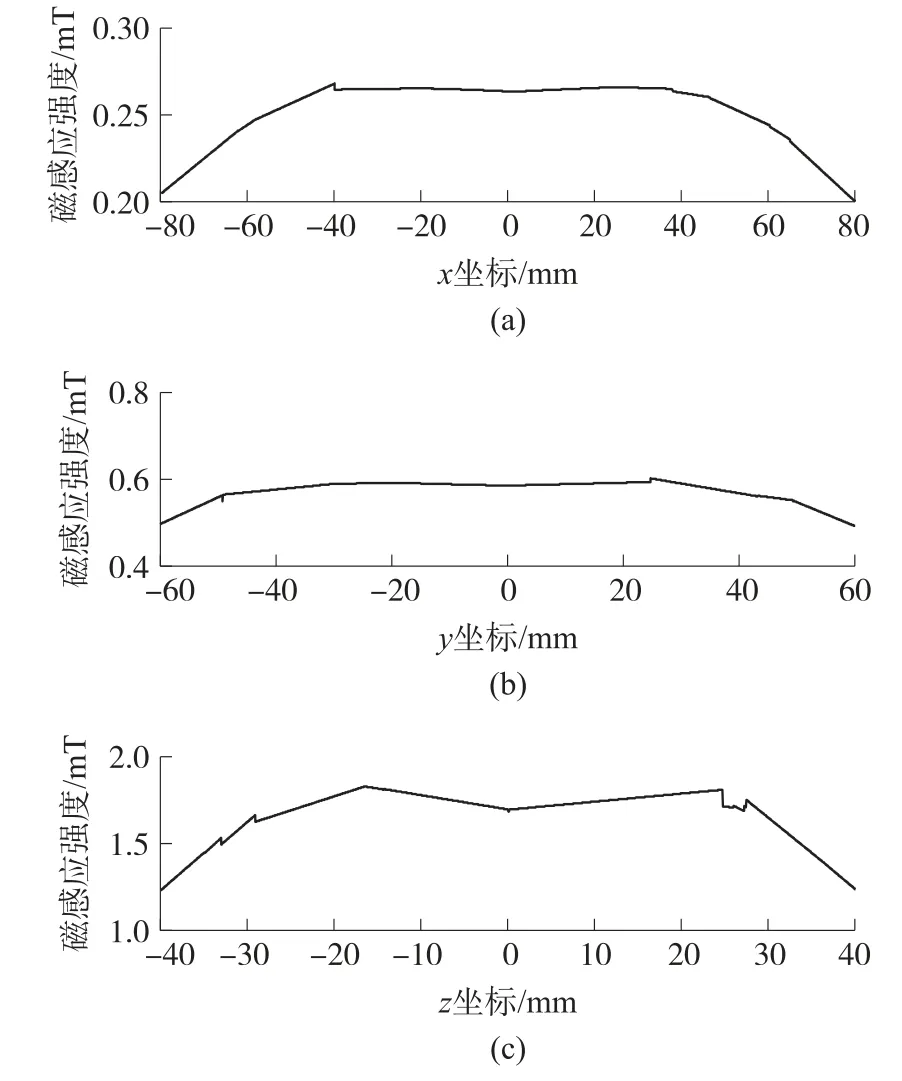
图10 线圈(MOPSO)磁感应强度分布

表7 中心区域磁感应强度RMS对比

由表7可知，NSGA-II算法对应线圈磁场具有更好的均匀性，而MOPSO算法对应的Y轴线圈补偿效率更高。因此，以NSGA-II算法的最优参数构建X轴线圈和Z轴线圈，以MOPSO算法的最优参数构建Y轴线圈。线圈的实际参数设置如表8所示。

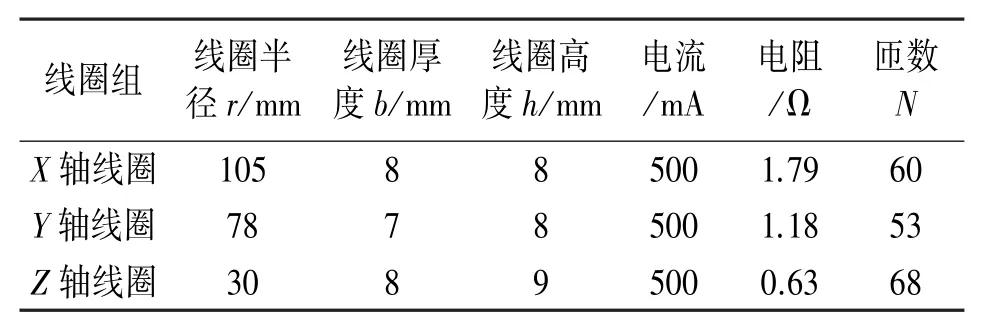
表8 三轴Helmholtz线圈实际参数

4 总结

根据MEMS电子罗盘强磁干扰补偿的实际需求，结合NSGA-II与MOPSO两种优化算法和COMSOL有限元分析，设计了一种优化的三维补偿线圈结构。首先分析了线圈的结构特性并对其建模仿真，确定了多目标优化变量。在此基础上，通过COMSOL和MATLAB联合仿真，以线圈总功30标优化算法对变量进行求解，并根据优化结果进一步确定了线圈的实际尺寸。仿真结果表明该三维补偿线圈产生的磁场均匀性良好，具有较高的补偿效率。