多步态SVM分类且自适应阈值的行人定位方法*

雷 明，李 擎，朱希安，付国栋

(1.北京信息科技大学自动化学院，北京 100192；2.高动态导航技术北京市重点实验室，北京 100192；3.北京德维创盈科技有限公司，北京 100192)

目前的行人导航方法主要有基于步长推算(Pedestrian Dead Reckoning，PDR)和 惯 性 导 航(Strapdown Inertial Navigation System，SINS)两种。PDR通过对步行者行走的步数、步长、方向、步进矢量进行测量和统计，可以推算出步行者行走轨迹和位置等信息，但只适用于有节律的行走和跑步状态，而SINS技术适用于各种步态下的行人导航。为减少惯性器件随时间积累的误差，目前，零速修正方法是SINS技术提高导航定位精度的主要技术之一。

传统零速检测方法一般的零速判别依据为三维加速度和角速度的模值或三维加速度窗口方差。文献[1]用了多条件约束的方法判定零速区间。固定阈值法在不改变运动步态条件下虽然能准确地判别零速区间，但实际情况中行人运动状态的多样性会影响零速判别的准确度。

检测的零速区间精确程度直接影响到系统误差修正的效果。因此，苑宝贞[2]等提出在每一个步态区间根据惯性测量器件足部数据和运动学的贝叶斯网络来估计零速区间，这种方法虽然能提高零速修正的鲁棒性，但是在行人快速行进时，贝叶斯网络估计精度下降。贾铮洋[3]等提出一种混合运动模式下的双重阈值检测方法，利用角速度变化曲线特点来匹配三种运动状态下对应的数据和窗口阈值，来判断零速区间。这种方法虽然在识别零速区间上有效，但在未知的运动状态下，无法识别出对应的阈值。王晓雷[4]等利用支持向量机分类决策的方法分析和训练足部的数据，建立超平面把步态分为静止区间和摆动区间。这种只区分摆动和静止区间的方法虽然在行走步态的轨迹数据中可以有效的抑制误差，但跑步、行走等多种步态同时切换下不同运动零速时所对应特征不同，所以分类效果较差。吴哲军[5]等也提出了基于支持向量机对行人行走和跑步状态实时步态分类的方法。此类方法的无法满足人在一般情况下多步态同时切换的问题，只针对于行走和跑步两种。Clara Piris[6]等人实现了SVM和k邻近分类器对行人跑步和行走运动的步态分类方法并对两种方法进行对比。目前现有的SVM决策方法只在行人行走、跑步运动模式识别的精度较高，但针对上下楼运动的分类精度还有待提升。

综上所述，本文提出一种多步态SVM分类且自适应阈值行人导航方法，利用多分类支持向量机方法把惯性器件输出的数据输入到本文已训练好的模型中进行训练以及分类，在已知行人上下楼运动状态后，通过气压计高度信息判断上下楼运动模式，根据行人运动分类结果将对应步态下的阈值进行自适应调节，确定不同步态下的零速区间。经实验证明，该方法改善了传统方法的不足，能够有效提高零速修正算法的精度。

1 零速区间检测

1.1 零速步态的判别

在行人步行运动过程中，行人行走的运动步态可分为摆动阶段和静止阶段。零速检测方法是利用传感器三维加速度和角速度的模值、方差和设定阈值进行比较，从而得到运动过程中静止区间。这时在理论上加速度和角速度的值处于平稳几乎为零，但是由于惯性传感器的漂移和噪声造成加速度和加速度信息非零，此时需要触发零速修正进行误差修正。本文采用加速度和角速度信息联合判定的方法来判定零速步态的区间[7]。k时刻的零速判定公式为:

式中:T(k)为k时刻加速度和角速度的函数；γ为零速判定阈值；w为时间窗的宽度；σω为角速度测量误差标准差；σa为加速度测量标准误差标准差；g为重力加速度；w(l)和a(l)分别为时间窗内l时刻的角速度和加速度值；为2范数；ma为时间窗内所有样本的加速度平均值。

1.2 最优阈值的选取

在传统的零速修正算法中，就是综合分析运动轨迹选用一个固定的阈值来判别零速区间，进而触发零速修正。图1(a)~1(e)是在不同运动步态下T(k)的变化。

图1 不同运动状态下T(k)变化曲线

图2是多运动模式下固定阈值判定零速区间的结果。阈值选取的是否准确是零速区间判定的关键。

图2 固定阈值零速区间检测

由图2可见(高状态为零速时刻，低状态为非零速时刻)，过高阈值导致把行走的摆动区间判定为零速区间，零速区间的误判影响零速修正的效果。针对上述情况，在本文中需要分别分析5种步态T(k)的变化特点，利用遍历的方法进行最优阈值的选取[8]。首先，根据T(k)确定最低点和次最低点对应纵坐标值y1和y2；然后，将零速判定阈值γ从y1到y2以Δy为间隔依次遍历，并依次输入相应的定位结果。按照遍历的方法先对不同的运动方式进行最优阈值的选取，为后续自适应零速检测算法做铺垫。如表1是对实验者5种运动类别进行最优阈值选取的结果，从中可见行走和跑步运动模态阈值明显比上下楼运动阈值得数量级大得多。根据数据分析可得，传统固定阈值的零速检测方法对于不同运动模态并不适用。

表1 不同步态阈值的选取例

2 多分类支持向量机算法

2.1 软间隔支持向量机

支持向量机[9]由于具有泛化性好、适用于小样本和高维特征等优点，所以被广泛应用于各种实际的步态分类问题和回归问题。一般惯性器件输出的加速度和角速度信息都不是线性的，所以本文选用的是能够处理线性不可分问题的软间隔支持向量机。支持向量机的原问题是在样本映射的高维空间内找到一个能把每一个样本正确分类的超平面，并且要使这类样本中离超平面距离最近的样本尽可能远离超平面。假设训练样本为Tr(xi，yi)，xi为n维的特征向量，yi为取值为＋1或-1的特征标签。为了寻找一个方程为wTx＋b＝0的最优分类超平面，必须满足以下条件:

①对于正样本有wTx＋b≥0，对于负样本有wTx＋b<0。

②超平面离两类样本尽可能远。每个样本到分类超平面的距离为。

上边两个条件可以转换成一个带约束的最小值问题:

因为目标函数的Hessian矩阵是严格正定的矩阵，它的可行域是一个凸集。因此这个优化问题是一个凸二次规划问题。为了满足能够解决线性不可分的问题，所以加入松弛变量ξi和惩罚因子C对违反不等式约束的样本进行惩罚。

ξi≥0，i＝1，2，…，l

不等式满足强对偶条件，考虑到对偶问题。然后构造拉格朗日函数:

固定乘子变量，分别对w、b、ξ分别求偏导并令它们等于零，再代入拉格朗日函数中得到关于α，β的函数。再根据条件等价最优化问题并求解。将求解的w的值代入超平面函数从而得到分类决策函数为:

考虑到原问题中两个不等式的约束和KKT条件，在最优点所有样本必须满足下面条件:

对于处理非线性问题，主要利用核映射的方法把特征向量变换到更高维度的空间，并在特征空间中找到最优的分类曲面。本文选用的是核函数为高斯核函数:

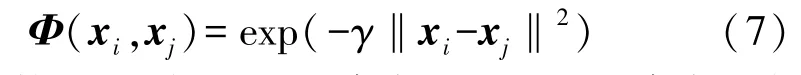
核函数必须满足KKT条件和Mercers条件，才能保留特征空间的几何解释，以便目标函数的解在特征空间中提供超平面。为向量加上核映射后，求解后得到的分类函数为:

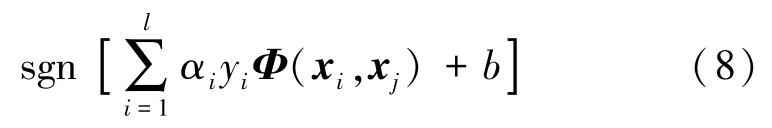
2.2 多分类支持向量机

经典的支持向量机只能解决二分类问题。对于处理多分类问题而不是二分类问题，支持向量机还是存在问题。对于多分类的问题现有的方法分两类:组合构造多个二分类器和直接优化多类分类的目标函数。构造多个而分类器的方法目前有:一对剩余方案、一对一和导向无环图方案等。根据所要对五种运动步态识别，本文采用一对一(OAO)的方案来实现[10]。假设对于有k类的分类问题，对每两类样本两两组合进行训练，构造k(k-1)/2个二分类器。训练时把每个组合中第i类作为正样本，其他各类依次作为负样本，总共训练个分类器。分类时采用投票的方法作为判定分类的结果。即用每一个二分类器对样本进行预测，如果判定为第n类，则第n类票数加1，得票最多的那一类作为预测的分类结果。算法流程如下:

Step 1 构造k(k-1)/2个SVM二分类器

Step 2 两两组合训练k(k-1)/2个SVM分类器如(1，2)(1，3)…(1，k)(2，3)(2，4)…(k-1，k)。

Step 3 选择一个最高票数的结果。

3 零速修正算法

本文选择传统的零速修正算法(ZUPT)对本文零速检测和传统阈值零速检测所定位结果进行对比。传统零速修正是以三维速度作为系统的观测量，用扩展卡尔曼滤波进行估计9维状态误差[11]。

本文选取9维状态量，如公式所示，

式中:δP、δv、δφ为惯导位置误差、速度误差、姿态误差在导航坐标系E-N-U坐标系上的三维分量。(其中，姿态δφ包括δα航向角、δβ姿态角、δγ横滚角)；状态转移矩阵Φk，k-1为9×9维，式中，I为3×3的单位矩阵；0是零矩阵。

噪声驱动矩阵的离散形式为:

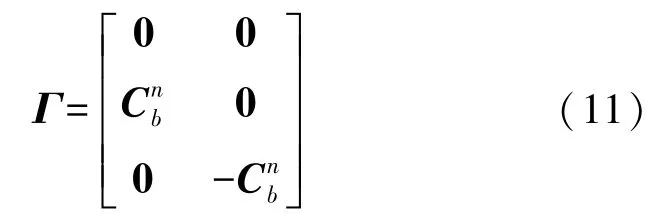
对于速度误差补偿，当检测到行人处于零速状态时，理论上此刻脚的速度为零，但由于存在测量等误差，此刻惯性传感器的测量值并不为零。将惯性传感器测量的实际速度与理论速度做差，得到的差值作为此刻的速度观测量，

观测矩阵为，

4 零速检测算法的自适应阈值调节

4.1 原始数据的滤波和特征提取

原始数据预处理和提取特征向量的过程是SVM模型训练以及分类的关键的一部分。利用MENS-IMU集成的三轴加速度、三轴角速度安装在行人脚部获取行人的运动数据信息。由于设备开关时或行人运动时抖动会导致设备采集的数据中产生脉冲干扰和随机噪声，影响数据的准确度，利用加窗和平滑滤波方法对原始数据进行预处理。

对原始数据滤波后，为了实现对5种运动步态模式的识别，需要对窗口内上述预处理的数据进行特征向量的提取。因为使用许多非相关性变量会导致过度拟合和过大的计算量。存在许多特征选择技术:相关系数，RF，主成分分析(PCA)，逻辑回归，RFE(无交叉验证的递归特征提取)或RFECV(有交叉验证的递归特征提取)和独立性测试(卡方)参考文献[12]详细介绍了特征生成和选择的理论。

本文数据特征值的提取[13]主要包含以下几种:范数、均方根误差、平均绝对误差、方差、皮尔逊相关系数。①加速度和角速度范数；②、和；③和；④ρay，az和ρax，az；⑤和。

均方根误差:

平均绝对误差:

方差:

皮尔逊相关系数:

ρay，az为加速度样本x轴和y轴数据之间的相关系数。

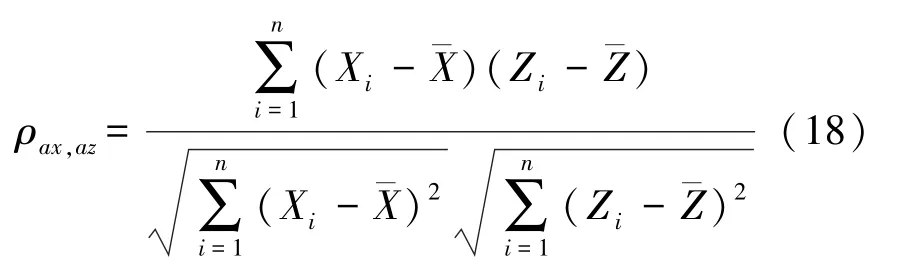
ρax，az为加速度样本z轴和y轴数据之间的相关系数。

四分位距IQR:即把所有数值由小到大排列并分成四等份，处于三个分割点位置的数值就是四分数。第三四分位数(Q3)，又称“较大四分位数”，等于该样本中所有数值由小到大排列后第75%的数字。

4.2 多分类支持向量机的阈值自适应调节

把提取的特征值和于其对应的运动步态标签输入到多分类支持向量机中对其模型进行训练，训练完成得到分类的决策函数。针对在行人多运动步态下传统方法中阈值不能调节导致定位精度差的问题，用多分类支持向量机模型对脚步的惯性器数据信息进行投票分类，再结合高度信息分类上下楼运动状态，根据识别出行人运动状态调节在其状态下对应的零速判别阈值，实现阈值的自适应调节。

4.2.1 多分类支持向量机模型训练:

构造个数为n＝10的二分类器，采集在五种行人脚部惯性器件的原始数据，分别为行走、跑步、静止、上楼、下楼，对采集的五种模式下的原始数据进行加窗预处理和特征提取，得到5种运动步态的特征向量。将5种步态的特征向量和对应的特征标签两两组合分别输入到10个二分类器中进行训练。

针对高斯核函数参数g和惩罚因子c难以确定，进而对模型性能影响大的问题，本文采用PSO优化算法对SVM模型参数进行优化。参数优化结果如图3所示。

图3 PSO-SVM参数优化结果

经过PSO算法优化后，得到最优的高斯核函数参数g＝32.362 6，惩罚因子c＝996.602 6。支持向量机的准确率为87.647%。

本文应用的训练样本总数量为2 500个，行走500个，跑步500个，静止500个，上楼500个，下楼500个。5种运动模式的分类标签分别为:行走<1>，跑步<2>，静止<3>，上楼<4>，下楼<5>。得到训练好的模型后，为了验证其分类效果，利用10 000个测试样本检验其分类器的准确率，表2为测试分类结果。其中上下楼运动模式测试样本得准确率均较低，但是其总体平均准确率可达到89.94%。

表2 多分类支持向量机模型测试结果

4.2.2 多分类支持向量机的阈值自适应调节

SVM对上下楼运动状态的分类效果并不好。为了更准确地确定上下楼运动状态模式，在得到分类器对5种运动模式分类结果后，上下楼分类结果需要根据窗口内气压计的高度信息来确定上下楼运动。在获取5种模式对应的阈值的基础上，实现对多运动模式的室内行人运动轨迹零速阈值自适应调节，需要将相应的零速修正的阈值赋予对应轨迹进行零速检测，进而触发零速修正算法。其过程如下:

Step 1 输入一段行人运动轨迹的原始加速度和角速度数据，并进行滤波平滑处理。

Step 2 对数据进行加窗处理，每个窗口数据算一组数据，分为n组。

Step 3 每一组数据做步态特征提取，并将步态特征向量输入训练好的多分类支持向量机模型中，对行人的步态模式进行投票预测。

Step 4 判断分类结果中是否为上下楼运动，再根据气压计窗口内得到高度信息判断上下楼运动的状态。

Step 5 将分类结果和上节对应运动模式已选取的最优阈值结合。根据对应阈值判别对应的零速区间，触发零速修正算法，利用扩展卡尔曼滤波对速度，位置进行校正。

Step 6 输出校正后的行人运动轨迹。

为了验证多分类支持向量机的阈值自适应调节方法的可行性，针对一段行人混合运动模式的轨迹，进行下述实验。首先，让行人在水平地面上持续跑步30 s，然后停止运动并保持静止15 s，最后让行人保持行走状态30 s。对上述实验得到的运动轨迹进行阈值的自适应调节，结果如图4所示。

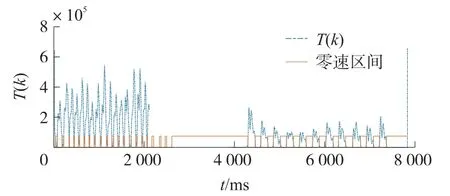
图4 人在跑步和行走时自适应阈值判定零速区间结果

5 实验结果与分析

5.1 总体的技术流程

本文总体技术流程如图5所示:①首先将输入的行人足部数据进行加窗和特征提取。②将提取的特征向量输入到上节训练好的多分类支持向量机中进行分类，并将根据气压计信息判定分类结果自适应调节零速检测的阈值。③触发零速修正算法。

图5 总体技术流程图

5.2 定位结果分析:

5.2.1 自适应阈值结果分析:

为了验证本文中方法的可行性，利用实验室自研的MENS-IMU惯性器件在实验室进行试验。实验时，采用足绑式IMU的方式进行室内行人混合运动实验。如图6所示:

图6 MENS-IMU器件以及安装方式

实验场地选在学校的实验室，运动起点选在实验室的4楼楼梯口处，首先进行从4楼下楼，到达一楼时停止15 s，接着沿着室内持续跑步两圈同样的轨迹，然后从原下楼的楼梯上到4楼，到达4楼停止5 s后继续沿室内行走一圈然后回到出发点。经过自适应零速阈值调节后，零速区间检测下图7所示:

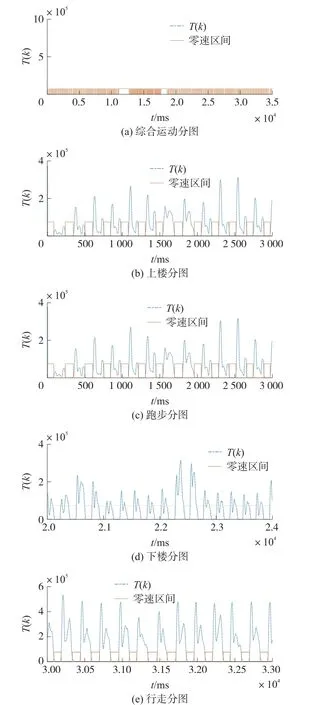
图7 五种运动切换时自适应阈值检测

一个步态周期中T(k)存在一个次最低点和一个最低点。而零速区间是在最低开始到最低点结束。如上图实验中零速检测结果，对于常规三条件法(图8和图9)与自适应多步态零速检测法进行对比得知，传统零速检测法在上楼、下楼时刻出现大量错误检测，整个上楼期间大部分的摆动区间被误检测为零速区间；是因为跑步时过高的阈值大于上下楼次最低点T(k)的值，导致摆动区间也被检测为零速区间。而自适应阈值多步态零速检测条件下，在零速时刻达到高精度的零速检测效果，并且零速区间准确率几乎达到100%。

图8 上楼时传统固定阈值零速阈值检测

图9 下楼时传统固定阈值零速阈值检测

5.2.2 定位结果分析:

图10包含多分类SVM算法的5种运动状态轨迹运动分类结果以及自适应阈值定位的结果。

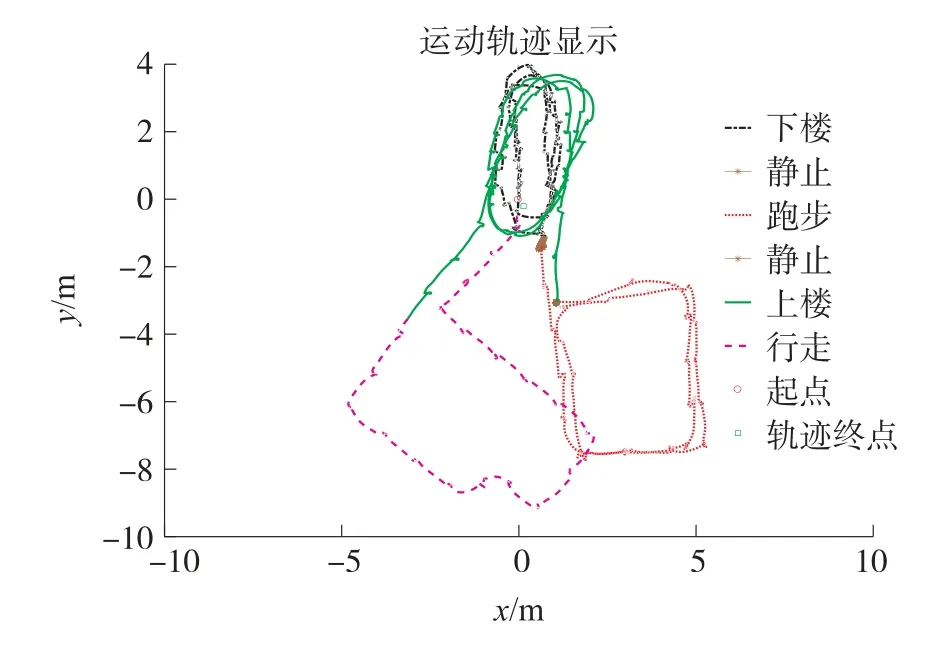
图10 五种运动切换时自适应阈值轨迹和分类结果

图11为其定位结果对应的解算速度与时间的关系。传统零速修正算法和SVM自适应阈值方法对比定位结果如图12所示。

图11 解算速度和时间的关系

图12 混合运动下两种方法定位结果

实验结果表明，引入本文提出的SVM自适应阈值方法定位结果在水平二维空间定位误差为0.2 m，0.2%，竖直方向上的定位误差为0.44 m。定位精度远远高于传统固定阈值的方法的定位结果。图12结果中，由于固定阈值为行走时阈值，则在上楼和下楼时零速区间出现很多误判，跑步时零速区间出现偶尔漏检的情况，导致定位精度下降。而多分类SVM方法可以将5种运动模式分类，再根据结果进行阈值的调节，进而提高定位的精度。

6 结论

本文针对行人在混合运动模式下传统零速修正算法定位精度差的问题，提出一种多步态SVM分类且自适应阈值的行人导航方法。由多分类SVM对预处理和特征提取的行人足部原始数据进行分类，再结合气压计信息区分上下楼运动，然后针对不同的分类模式进行最优阈值的调节，进而检测出更准确的零速区间触发零速修正，最后输出定位结果。实验结果表明，本方法对行走、跑步、静止、上楼、下楼五种模式的总体平均识别率已达到了89.94%，行人在多运动模式下的二维空间定位精度达到了0.2 m，竖直方向达到了0.44 m。