MCNP与GEANT4应用于随钻方位伽马测井仪探测性能对比

彭礼韬,张立国,郝琦,玉宇

(1.华北电力大学核科学与工程学院,非能动核能安全技术北京市重点实验室,北京102206;2.清华大学核能与新能源技术研究院,教育部先进反应堆工程与安全重点实验室,北京100084)

0 引 言

核测井是以核物理学和核物理技术为基础,利用岩石及其孔隙流体的核物理性质,研究测井钻孔地质剖面的地球物理方法[1]。随着石油勘测与开采规模不断增大,定向水平井和大斜度井的应用推广十分迅速,随钻方位伽马测井已成为一项常规测井项目。随钻方位伽马测井以随钻自然伽马测井为基础,自然伽马测井通过测量分析岩层中放射性元素(U、Th、K)原子衰变放射出的伽马射线,得到地层岩性;方位伽马测井除此之外还能测量方位信息,通过将测量数据分到不同的方位扇区,不仅可以提供地层岩性信息,还能反映测量数据的方位特性,从而即时绘制地层成像,引导钻井路线,保证正确地勘测到目标地层。

国外的随钻方位伽马测井技术发展较早,目前仪器的设计与研究已经相当成熟,测井方法和软件的研究也较为领先。中国随钻方位伽马测井技术和国外有一定差距,仪器需进一步优化[2]。仪器优化需要反复修改仪器各部分的设计及尺寸来获得最好的仪器性能,需要快速进行仪器设计进度和性能响应特征的测量,为节约时间、降低成本,采用蒙特卡罗模拟方式进行仪器的优化是最佳选择。

在核测井领域,最常用也最为成熟的模拟工具是MCNP(Monte Carlo N Particle Transport Code),MCNP是能够模拟连续能量的中子、光子、电子在任意几何形状模型中的输运过程且考虑时间因素的大型通用模拟软件[3]。MCNP在中国的使用存在部分局限性,例如其建模方法在某些情况下略显复杂或难以实现,因此,寻找一个能够与其互相补充、适用于不同情况的蒙卡模拟软件是必要的。GEANT4是一个采用面向对象技术构建的蒙特卡罗通用程序包,由于其面向对象的优越性,应用范围已经超越了高能物理的界限,在核物理实验模拟、加速器物理、空间物理和医学物理等各个领域中都得到了广泛应用,但GEANT4在核测井领域还没有得到广泛采用[4]。本文利用MCNP和GEANT4分别对某一方位伽马测井仪器模型进行性能响应特征的分析,并考察二者在模拟过程中的表现,对比二者的测量结果精度,验证GEANT4在核测井模拟中的适用性。

1 计算模型

本文建立模型及计算所使用的软件为MCNP4C和GEANT4.10.5。在不影响粒子主要路径的同时对模型进行适度简化,MCNP计算模型的正视图及剖面见图1。模型采用单晶体探测器,部分关键参数见表1。测量地层为标准井中具有高放射性的围岩层,含有一定量的U、Th、K放射性核素,井眼中填充淡水作为井眼液。

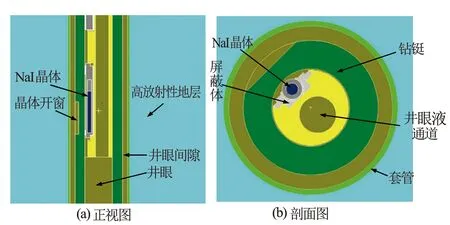
图1 MCNP模型

表1 模型参数

GEANT4模型对仪器进行不同程度的简化,各项参数与MCNP模型一致。尽管二者皆采用布尔运算来建立几何模型,但过程却相差极大。MCNP采用对曲面做布尔运算得到不同的几何体,根据建模需要,通过计算得到不同曲面解析式的参数,同时赋予该几何体材料、密度等物理信息。GEANT4则是自行创建简单几何体,并将其放置在空间内指定位置,对于复杂结构可以通过简单几何体进行布尔运算得到,也可以对几何体进行绕轴旋转处理。同时,GEANT4支持自动建模,可利用CAD模型转换完成GEANT4的几何模型[5],不仅可以提高建模效率和模型的真实性,还能减少简化模型带来的错误与偏差,缺点是对于精度极高、结构复杂的模型可能存在模拟效率较低的问题。

2 模型的实验验证

在进行性能响应特征的计算之前,对所建仪器模型和地层抽样方案进行实验验证,确保模拟结果符合仪器的实际性能。标准井中主要考虑3种放射性元素:238U,232Th,40K。其中,40K仅考虑1.46 MeV的γ射线;对于已经达到衰变递次平衡的238U和232Th,其衰变链上有十余种不稳定的核素,为了得到准确完整的238U和232Th的γ能谱,必须要对其进行一一考虑。使用GEANT4的G4 Radioactive Decay Physics类模拟达到衰变递次平衡的238U和232Th衰变链的γ能谱。统计N个母核衰变,得到的γ能谱除以N,就是当有一个母核裂变时放射出来γ光子的分布;按照该γ射线能量分布抽样γ光子,进而模拟γ光子的输运过程。按照上述思路,模拟107个238U、232Th母核的裂变过程,得到的γ能谱见图2,γ的能量取值为0～3.3 MeV,可见其能谱相当复杂。在模拟过程中,根据放射性核素的含量选择能谱并进行抽样即可达到模拟效果。

考察MCNP和GEANT4模型在高放层中计数率与实验结果的相对误差(见表2),二者模拟结果与实验结果的误差都在±5%以内,证明几何模型与地层模型均无较大偏差,所得模拟数据可靠。

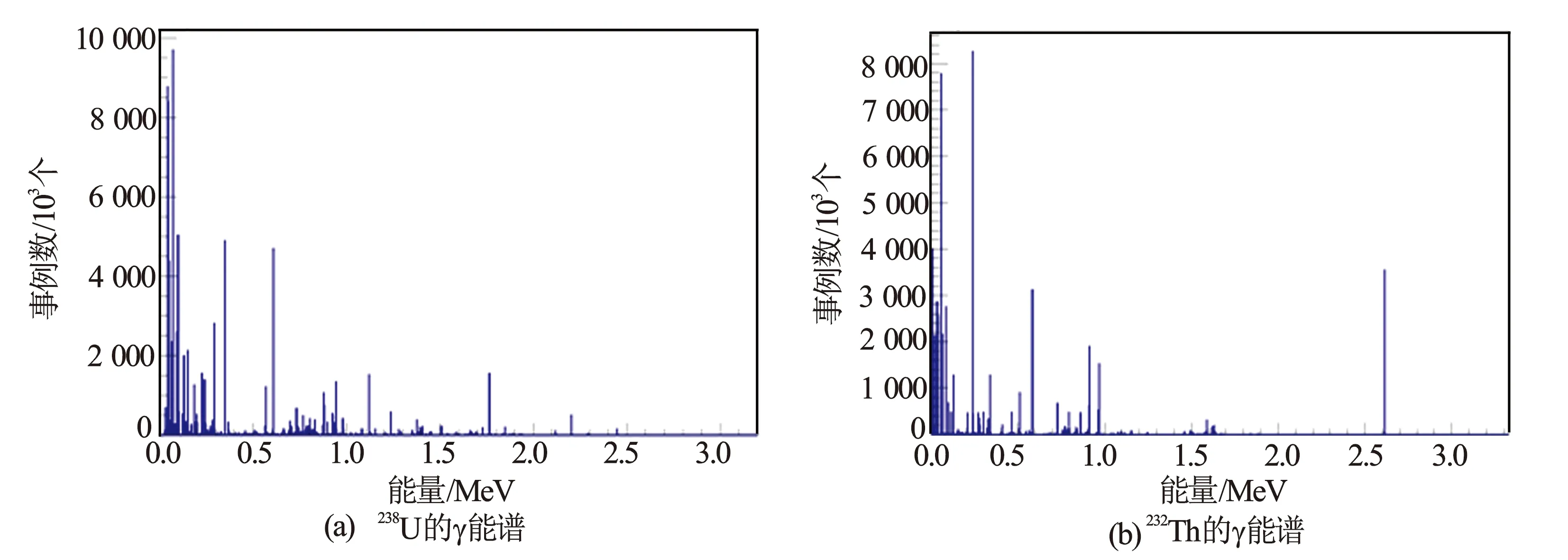
图2 模拟输入得到的γ能谱

表2 实验与模拟结果对比

对MCNP和GEANT4输出的能谱进行对比[6](见图3),二者谱形符合较好,在能量低于1 MeV时,特征峰相互重叠,比较难以分辨,但二者对于能量较大的特征峰都表现良好,如K的能量为1 461 keV、U的能量为1 764 keV和Th的能量为2 614 keV这3个特征峰,无过多干扰,分辨率较高。这说明GEANT4作为核测井模拟工具不论是模拟过程的准确性或是输出结果的可靠性都是合格的。

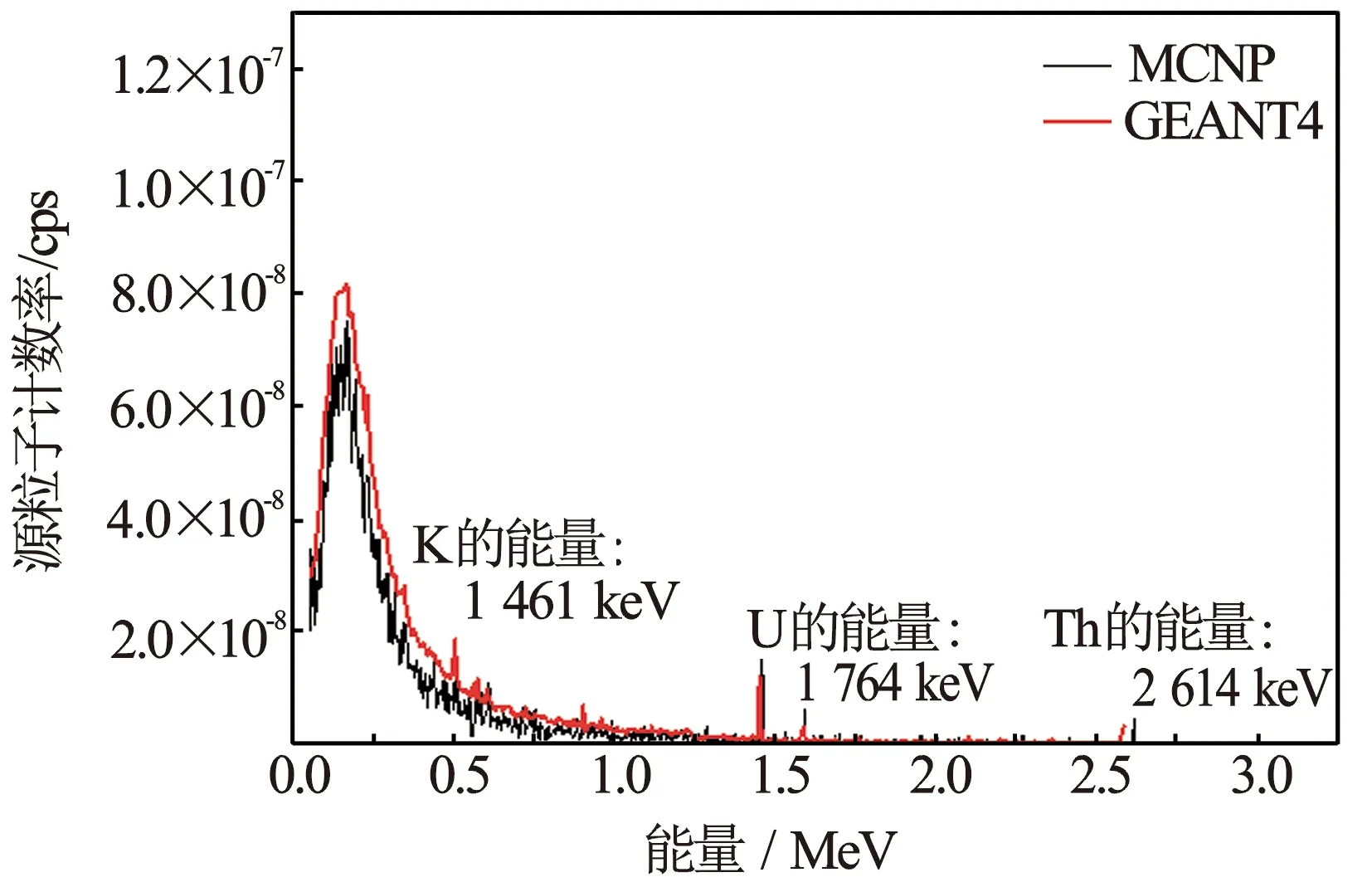
图3 输出能谱对比

3 仪器性能响应特征计算

通常用以判断仪器性能好坏的响应特征参数为径向分辨率、纵向分辨率以及方位分辨率[7-9]。对于方位伽马测井仪器,为了得到良好的性能响应特征,需要取得较大的径向探测深度、较小的纵向分辨厚度和较小角度内较高的方位分辨率,同时需要有较高的探测效率来保证相对较低的统计误差。

在方位伽马测井仪器的晶体中心位置与高放层中心重合的几何布局下进行径向探测深度等仪器性能响应特性参数分析。GEANT4从模拟过程记录的粒子位置信息,统计在探测器上造成有效计数(能量沉积事件)的源粒子在地层中的初始位置分布,计算性能响应特征。使用MCNP进行性能响应特征计算时,需逐步增大地层中粒子抽样范围,如增大抽样半径、纵向厚度等,测量其积分几何因子[10]。

3.1 径向探测深度

通常将径向积分几何因子达到0.9时所对应的半径定义为径向探测深度,径向探测深度表征探测器对地层中放射性物质发出射线的径向探测响应能力,径向探测深度越大,径向分辨率越高。GEANT4可直接通过统计输出的粒子初始位置分布来测量径向探测深度[11-12]。在使用MCNP进行探测深度分析时,则模拟一个圆环柱地层,从地层内侧开始,维持内径不变,逐步增大地层中粒子抽样范围的外径,进行模拟和数据统计。

图4(a)为GEANT4统计的伽马光子初始位置半径的分布,从地层内径开始,随着半径增大,探测到的粒子量逐渐减小。将相应半径对应的径向积分几何因子进行统计画出曲线,并与MCNP的模拟点进行对比,如图4(b)所示,MCNP在抽样半径较小时,探测效率较高,统计误差较低,所得结果与GEANT4曲线符合较好;在半径较大时,统计误差增大,导致模拟结果略微波动。根据GEANT4分布得到的径向探测深度为228 mm(以井眼内壁为零点),而MCNP测量出来的径向探测深度近似为230 mm,二者结果非常接近。

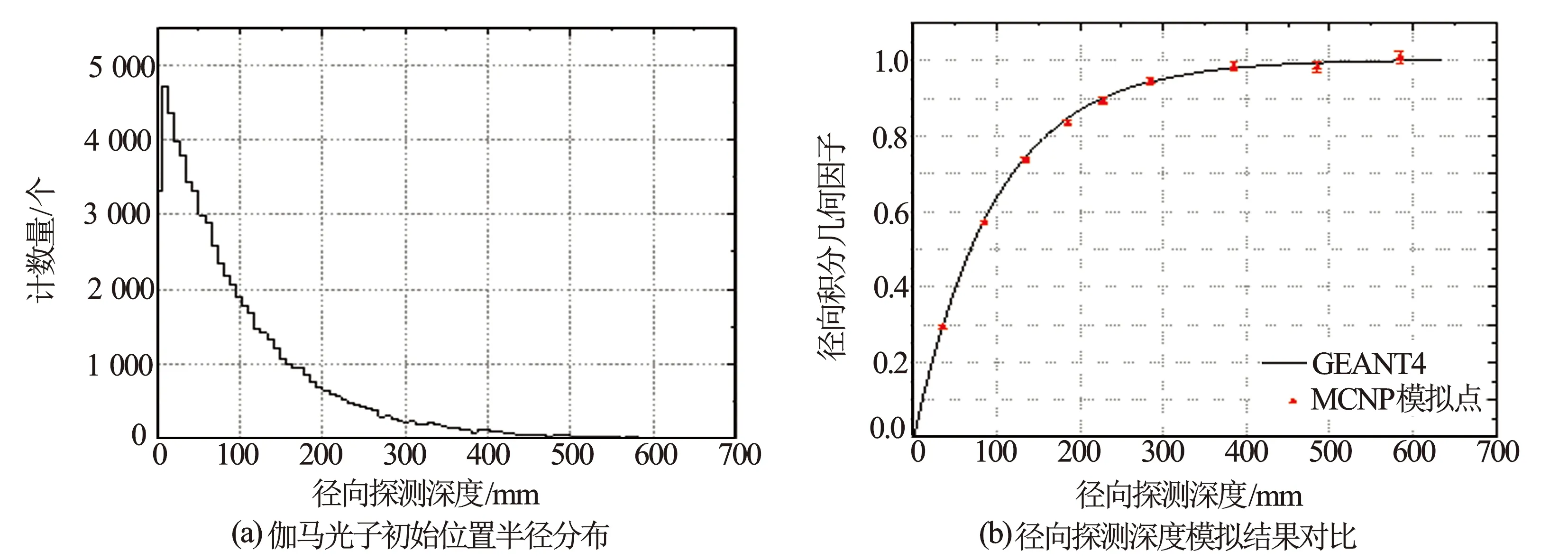
图4 径向模拟结果

3.2 纵向分辨厚度

在计算时取纵向积分几何因子为0.9的点对应的放射性层厚度为纵向分辨厚度,其表征仪器能分辨地层最小厚度的性能响应特征[6],纵向分辨厚度越大,纵向分辨率越小,仪器测量结果越容易受相邻不同地层的放射性影响。GEANT4可利用统计的粒子初始纵向位置分布直接计算得到纵向分辨厚度,而在使用MCNP进行探测深度分析时,模拟一个放射性薄层,逐步增大地层厚度,进行模拟和数据统计。

图5(a)为GEANT4统计的伽马光子初始位置纵向分布,纵向距离越大,粒子探测效率越低。将相应纵向距离对应的纵向积分几何因子进行统计画出曲线,并与MCNP的模拟点进行对比[见图5(b)]。在探测效率较高的部分,二者结果符合较好。随着径向距离的增大,数据点出现小幅波动,但对于纵向分辨厚度的测量来说影响不大。根据GEANT4分布得到的纵向分辨厚度为219 mm,而MCNP模拟测量的纵向分辨厚度近似为222 mm。

图5 纵向模拟结果

3.3 方位分辨角度

方位分辨角度表征仪器的方位角度探测范围,以晶体轴线和井眼轴线所在平面为0,统计来自方位角±θ范围内的方位积分几何因子,当方位积分几何因子等于0.9时,定义θ为方位分辨角度,而方位分辨率为探测器所面向的地层扇区对探测器总计数的贡献,方位分辨角度越小,则方位分辨率越高[13-15]。GEANT4可以通过计算源粒子位置分布的方式求取方位分辨角度。而用MCNP作为模拟工具时,需将地层分为16个扇区,每个扇区角度为22.5°,通过限制抽样扇区测量±22.5°到180°方位角时的计数占比。

通过分析GEANT4的模拟输出,得到的方位角分布见图6(a)。由图6可见,随着方位角角度增大,计数量先减小然后略有提升。出现该现象的原因:当角度较小时,随着角度的增加,两侧屏蔽体阻挡了该方向上的大部分射线;随着角度的继续增大,新增扇区的射线可通过后方钻井液通道进入探管,导致探测器计数量对该方向上的响应有所上升。GEANT4统计得出的方位分辨角度为105°,MCNP测量得到的方位分辨角度则为103°。表3为探测器所面向的地层扇区在不同角度时的方位分辨率。

图6 方位模拟结果

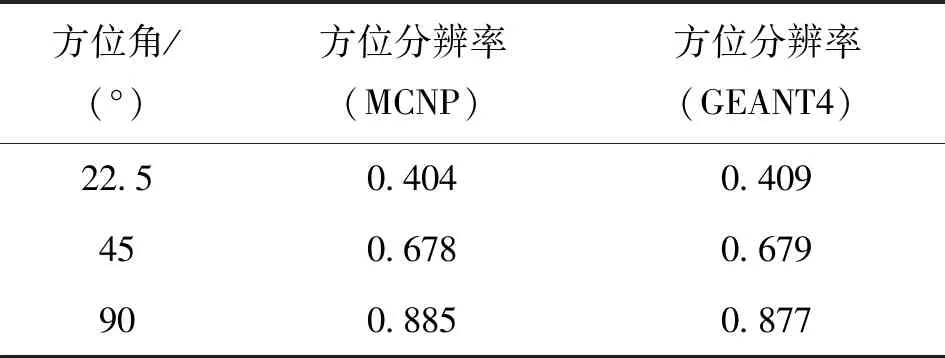
表3 不同方位角下的方位分辨率

4 对比与分析

从模型验证和仪器性能响应特征计算的结果上来看,GEANT4的谱形与MCNP基本符合,计算得到的性能响应特征数据也比较可靠,这与Nikolay等[4]所得的结论一致。GEANT4非常准确地模拟了自然伽马随钻测井中粒子输运的过程,仅有一些相对较小的偏差,差异的主要来源是用于模拟的核数据的多样性,插值算法和粒子输运模型的差异[4],这些偏差对于核测井应用是可以接受的。

在模拟计算过程中,由于GEANT4应用程序编程接口提供了创建特定应用程序的功能,可根据需要修改数值算法、修正程序、扩展物理或计算模型、追踪输出所需数据。因此,可在程序中对粒子初始位置的各项数据进行追踪统计和分析。这不仅为仪器性能响应特征分析提供便利,也利于提高数值分析准确度。

对二者的计算效率进行比较,在同一计算平台(Linux系统)上,将2种软件单核运行在相同环境下相同事例数的计算时间作对比。其中,GEANT4模拟5×109事例数所需时间为402.58 min,MCNP所需时间仅为94.2 min,二者的计算效率相差较大。分析表明造成如此差异的原因是GEANT4初始化(截面等)阶段耗时较长和磁盘读写较多,但GEANT4在多线程并行计算中表现优秀,随着线程数的增大,其计算效率呈线性提升[16],MCNP随着线程数的增大计算效率提升则不明显。因此,在实际的仪器优化或校正过程中,GEANT4模拟所耗费的时间可以接受。

在建模效率上,MCNP的几何模型建立比较简单,通过少量参数即可描述其几何模型,且学习成本较低。但在面对非规则几何体时,MCNP可能难以准确地建立该模型,同时,若是对仪器进行设计优化,MCNP用于描述几何体的语句比较抽象,二维可视化结构需要较好的空间想象,修改部分零件的参数时操作较为繁琐。GEANT4的手动建模对建模人员的技术要求较高,在编写程序方面需要花费更多时间,程序内容也更为冗长,但对于不需太过精密的仪器若采取自动建模,可大大节省建模时间[17]。而且GEANT4具有三维可视化模块,对于模型的确认更加方便形象,有利于找出建模过程中的几何错误加以修正。总体来说,在MCNP中描述1个栅元所需的面较少时,MCNP的效率比较高,但在对复杂几何体进行描述时,GEANT4建模的效率更高,二者在建模过程中存在各自优势,都能满足不同的建模精度要求。

5 结 论

(1)本文将随钻方位伽马测井仪器通过GEANT4和MCNP进行蒙特卡罗模拟,其模拟结果和输出能谱符合程度较好,根据模拟结果计算其性能响应特征,所得参数基本一致。

(2)GEANT4在进行几何建模时采用对简单几何体进行布尔运算的方式,更加灵活,不论是简单结构还是复杂结构都能较好的进行还原,且支持自动建模。

(3)GEANT4对于测井过程中粒子输运的模拟较为准确,所得模拟结果可靠。

(4)GEANT4程序在测量仪器的性能响应特征过程中效率更高,输出文件可统计粒子源的位置信息,利用统计信息可快速计算仪器性能响应特征,无需进行多次模拟。

(5)GEANT4作为一款通用、灵活的蒙特卡罗模拟工具,不仅适用于高能物理应用,在核测井领域也同样十分适用,它具有功能自由全面、支持自动建模、数据处理方便等优势。GEANT4提供了一种在MCNP使用存在困难时的蒙特卡罗模拟手段,在模拟过程中,既可根据具体需求和模拟效率选择不同的模拟工具,也可以将两者作为对比参照保证模拟的精确性。